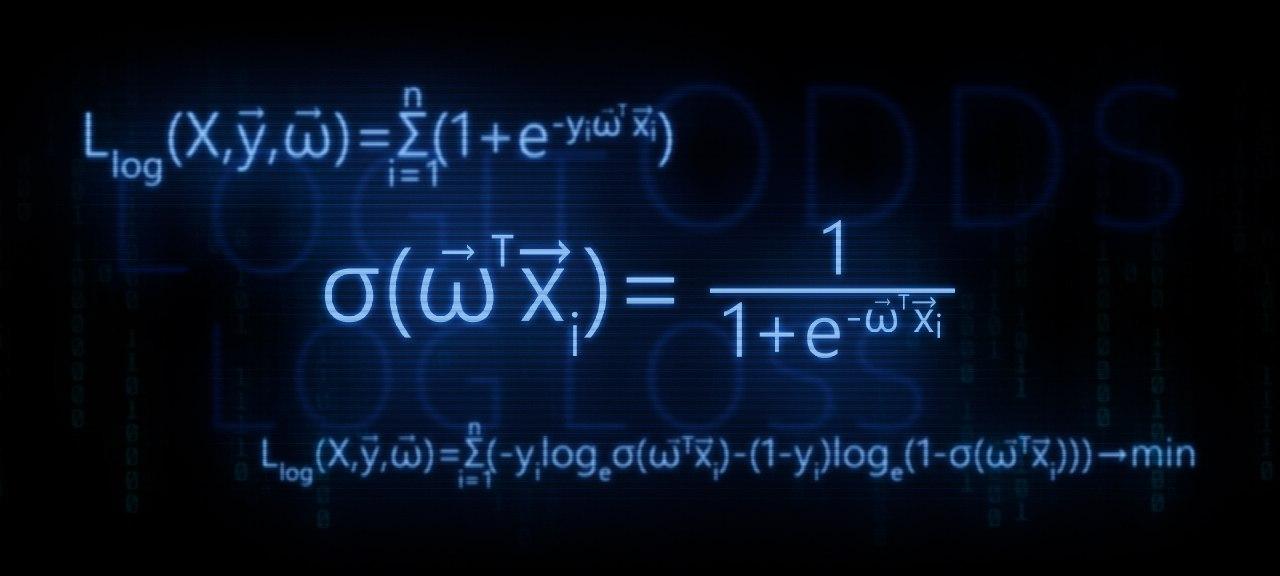
في هذه المقالة ، سنقوم بتحليل الحسابات النظرية لتحويل
دالة الانحدار الخطي إلى وظيفة تحويل السجل العكسي (بمعنى آخر ، وظيفة الاستجابة اللوجستية) . ثم ، باستخدام ترسانة
طريقة الاحتمالية القصوى ، وفقًا لنموذج الانحدار اللوجستي ، نشتق دالة الخسارة
Logistic Loss ، أو بمعنى آخر ، نحدد الوظيفة التي يتم من خلالها تحديد معلمات متجه الوزن في نموذج الانحدار اللوجستي
vecw .
الخطوط العريضة للمقال:
- لنكرر العلاقة الصريحة بين متغيرين
- نحدد الحاجة لتحويل وظيفة الانحدار الخطي f(w،xi)= vecwT vecxi لوظيفة الاستجابة اللوجستية sigma( vecwT vecxi)= frac11+e− vecwT vecxi
- نجري التحولات ونشتق من وظيفة الاستجابة اللوجستية
- دعونا نحاول أن نفهم لماذا تكون طريقة المربعات الصغرى سيئة عند اختيار المعلمات vecw ميزات الخسارة اللوجستية
- نحن نستخدم طريقة الاحتمالية القصوى لتحديد وظيفة اختيار المعلمة vecw :
5.1. الحالة 1: دالة الخسارة اللوجيستية للكائنات ذات التصنيف للفئة 0 و 1 :
Llog(X، vecy، vecw)= sum limitni=1(−yi mkern2muloge mkern5mu sigma5mu sigma( vecwT vecxi)−(1−yi) mkern2muloge mkern5mu(1− sigma( vecwT vecxi))) rightarrowmin
5.2. الحالة 2: دالة الخسارة اللوجيستية للكائنات ذات التسميات للفئة -1 و +1 :
Llog(X، vecy، vecw)= sum limitni=1 mkern2muloge mkern5mu(1+e−yi vecwT vecxi) rightarrowmin
المقالة مليئة بأمثلة بسيطة يسهل فيها إجراء جميع العمليات الحسابية لفظيًا أو ورقيًا ، وفي بعض الحالات قد تكون هناك حاجة إلى آلة حاسبة. لذا استعد :)
يستهدف هذا المقال بشكل أكبر علماء البيانات ذوي المستوى الأولي من المعرفة في أساسيات التعلم الآلي.
المقالة سوف توفر أيضا رمز لرسم الرسوم البيانية والحسابات. كُتب كل الكود في
بيثون 2.7 . سأشرح مقدمًا عن "حداثة" الإصدار المستخدم - هذا أحد الشروط اللازمة للحصول على دورة معروفة من
Yandex على منصة الإنترنت التعليمية التي لا تقل شهرة عن
Coursera عبر الإنترنت ، وكما قد تفترض ، تم إعداد المواد بناءً على هذه الدورة التدريبية.
01. خط مستقيم
من المعقول طرح السؤال - أين العلاقة المباشرة والانحدار اللوجستي؟
كل شيء بسيط! الانحدار اللوجستي هو أحد النماذج التي تنتمي إلى المصنف الخطي. وبكلمات بسيطة ، فإن الهدف من المصنف الخطي هو التنبؤ بالقيم المستهدفة
ذ من المتغيرات (التراجع)
X . ويعتقد أن العلاقة بين العلامات
X والقيم المستهدفة
ذ الخطية. وبالتالي اسم المصنف نفسه خطي. بشكل عام جدًا ، يعتمد نموذج الانحدار اللوجستي على افتراض وجود علاقة خطية بين الميزات
X والقيم المستهدفة
ذ . ومن هنا - اتصال.
الاستوديو هو المثال الأول ، وهو محق في ذلك ، حول الاعتماد المباشر للكميات المدروسة. في عملية إعداد المقال ، صادفت مثالًا أصابني بالفعل
التهاب في الحلق - اعتماد القوة الحالية على الجهد
("تحليل الانحدار التطبيقي" ، N. Draper ، G. Smith) . هنا سننظر فيه أيضًا.
وفقًا
لقانون أوم:I=U/R حيث
I - القوة الحالية
يو - الجهد
R - المقاومة.
إذا لم نكن نعرف
قانون أوم ، يمكن أن نجد التبعية تجريبياً عن طريق التغيير
يو والقياس
I بينما دعم
R الثابتة. ثم سنرى أن الرسم البياني التبعية
I من
يو يعطي أكثر أو أقل خط مستقيم يمر عبر الأصل. قلنا "أكثر أو أقل" ، لأنه على الرغم من أن التبعية دقيقة بالفعل ، فقد تحتوي قياساتنا على أخطاء صغيرة ، وبالتالي قد لا تقع النقاط على الرسم البياني تمامًا على الخط ، ولكن سيتم تناثرها بشكل عشوائي.
الرسم البياني 1 "الاعتماد
I من
يو "
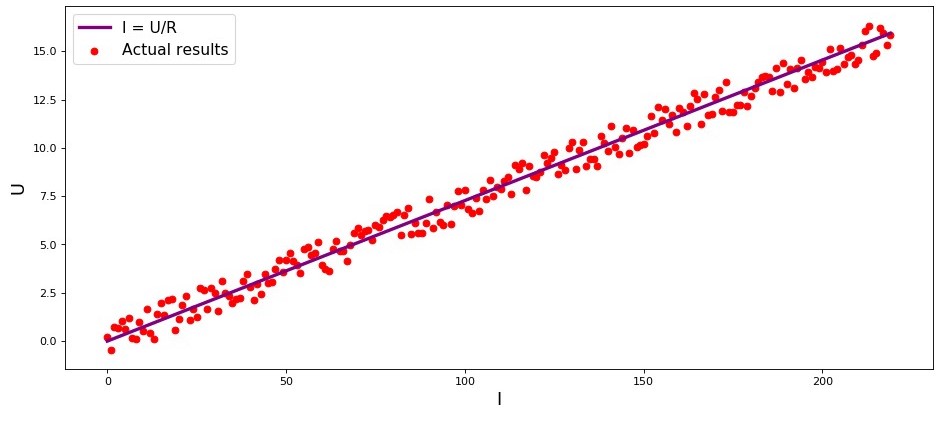
الرسم البياني تقديم رمزimport matplotlib.pyplot as plt %matplotlib inline import numpy as np import random R = 13.75 x_line = np.arange(0,220,1) y_line = [] for i in x_line: y_line.append(i/R) y_dot = [] for i in y_line: y_dot.append(i+random.uniform(-0.9,0.9)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(x_line,y_line,color = 'purple',lw = 3, label = 'I = U/R') plt.scatter(x_line,y_dot,color = 'red', label = 'Actual results') plt.xlabel('I', size = 16) plt.ylabel('U', size = 16) plt.legend(prop = {'size': 14}) plt.show()
02. الحاجة إلى تحولات معادلة الانحدار الخطي
النظر في مثال آخر. تخيل أننا نعمل في أحد البنوك وأننا نواجه مهمة تحديد احتمال سداد القرض من قبل المقترض ، اعتمادًا على بعض العوامل. لتبسيط المهمة ، فإننا نعتبر عاملين فقط: الراتب الشهري للمقترض والدفع الشهري لسداد القرض.
المهمة مشروطة للغاية ، ولكن مع هذا المثال ، يمكننا أن نفهم لماذا لا يكفي استخدام
وظيفة الانحدار الخطي لحلها ، وسنكتشف أيضًا ما هي التحولات مع الوظيفة التي تحتاج إلى تنفيذها.
نعود على سبيل المثال. من المعلوم أنه كلما زاد الراتب ، كلما كان المقترض قادرًا على التوجيه شهريًا لسداد القرض. في الوقت نفسه ، بالنسبة لمجموعة معينة من الرواتب ، سيكون هذا الاعتماد خطيًا تمامًا لنفسه. على سبيل المثال ، خذ مجموعة من المرتبات تتراوح بين 60،000 و 200،000 ونفترض أنه في النطاق المحدد للرواتب ، يكون اعتماد حجم الدفعة الشهرية على مبلغ الراتب خطيًا. لنفترض ، بالنسبة إلى مجموعة الأجور المحددة ، أنه قد تم الكشف عن أن نسبة الراتب إلى الدفعة لا يمكن أن تقل عن 3 وأن المقترض يجب أن لا يزال لديه 5.000 كاحتياطي. وفقط في هذه الحالة ، سنفترض أن المقترض سيعيد القرض إلى البنك. ثم ، تأخذ معادلة الانحدار الخطي النموذج:
f(w،xi)=w0+w1xi1+w2xi2،حيث
w0=−5.000دولا .
w1=1دولا .
w2=−3دولا .
xi1 -
الراتب i -th المقترض
xi2 -
دفع القرض i المقترض -th.
استبدال الراتب ودفع القرض مع معلمات ثابتة في المعادلة
vecw يمكنك أن تقرر ما إذا كنت تريد منح أو رفض قرض.
التطلع إلى المستقبل ، نلاحظ أنه ، لمعلمات معينة
vecw سوف تنتج
وظيفة الانحدار الخطي المستخدمة في
وظيفة الاستجابة اللوجستية قيمًا كبيرة تجعل من الصعب حساب احتمالات سداد القرض. لذلك ، يُقترح تخفيض معاملاتنا ، دعنا نقول ، 25000 مرة. من هذا التحويل إلى النسب ، لن يتغير قرار منح القرض. دعونا نتذكر هذه اللحظة للمستقبل ، والآن لجعلها أكثر وضوحًا ما نتحدث عنه ، سننظر في الموقف مع ثلاثة مقترضين محتملين.
الجدول 1 "المقترضون المحتملون"
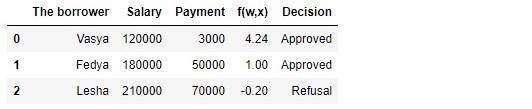
رمز لتوليد الجدول import pandas as pd r = 25000.0 w_0 = -5000.0/r w_1 = 1.0/r w_2 = -3.0/r data = {'The borrower':np.array(['Vasya', 'Fedya', 'Lesha']), 'Salary':np.array([120000,180000,210000]), 'Payment':np.array([3000,50000,70000])} df = pd.DataFrame(data) df['f(w,x)'] = w_0 + df['Salary']*w_1 + df['Payment']*w_2 decision = [] for i in df['f(w,x)']: if i > 0: dec = 'Approved' decision.append(dec) else: dec = 'Refusal' decision.append(dec) df['Decision'] = decision df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision']]
وفقًا للجدول ، فإن Vasya ، براتب 120.000 ، ترغب في الحصول على هذا القرض من أجل سداده بمبلغ 3.000 شهريًا. لقد قررنا أنه من أجل الموافقة على القرض ، يجب أن يكون راتب Vasya ثلاثة أضعاف حجم الدفع ، بحيث لا يزال هناك 5.000P. يفي Vasya بهذا المطلب:

. لا يزال هناك 106،000P. على الرغم من حقيقة أنه عند حساب
f(w،xi) قللنا من الاحتمالات
vecw 25000 مرة ، كانت النتيجة هي نفسها - يمكن الموافقة على القرض. سيحصل فيديا أيضًا على قرض ، لكن ليشا ، على الرغم من أنه يحصل على أكثر من غيره ، سيتعين عليه كبح شهيته.
دعونا رسم جدول زمني لهذه القضية.
الرسم البياني 2 "تصنيف المقترضين"
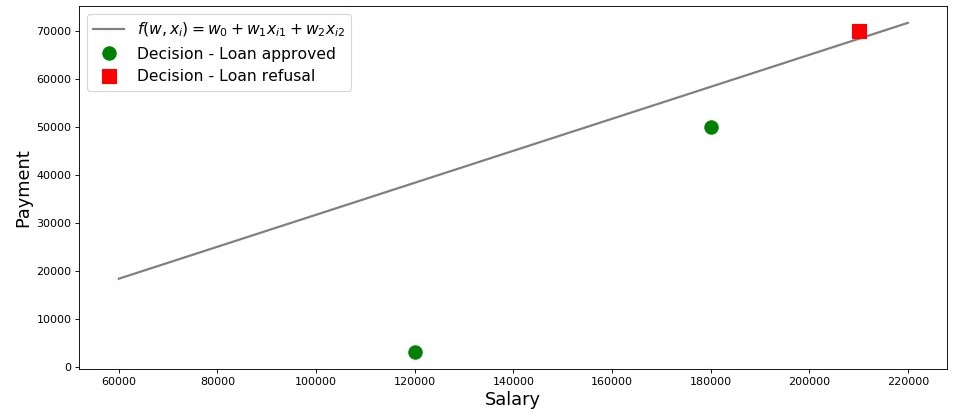
رمز للتخطيط salary = np.arange(60000,240000,20000) payment = (-w_0-w_1*salary)/w_2 fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(salary, payment, color = 'grey', lw = 2, label = '$f(w,x_i)=w_0 + w_1x_{i1} + w_2x_{i2}$') plt.plot(df[df['Decision'] == 'Approved']['Salary'], df[df['Decision'] == 'Approved']['Payment'], 'o', color ='green', markersize = 12, label = 'Decision - Loan approved') plt.plot(df[df['Decision'] == 'Refusal']['Salary'], df[df['Decision'] == 'Refusal']['Payment'], 's', color = 'red', markersize = 12, label = 'Decision - Loan refusal') plt.xlabel('Salary', size = 16) plt.ylabel('Payment', size = 16) plt.legend(prop = {'size': 14}) plt.show()
لذلك ، لدينا خط ، شيدت وفقا للوظيفة
f(w،xi)=w0+w1xi1+w2xi2 ، يفصل المقترضين "السيئين" عن "الجيد". أولئك المقترضين الذين لا تتوافق رغباتهم مع الفرص هم فوق الخط المباشر (ليشا) ، أولئك الذين لديهم القدرة على سداد القرض وفقًا لمعايير نموذجنا هم تحت الخط المباشر (فاسيا وفيديا). خلاف ذلك ، يمكننا أن نقول هذا - لدينا خط يقسم المقترضين إلى فئتين. نشير إليها على النحو التالي: إلى الفصل
+1دولا صنف هؤلاء المقترضين الذين من المحتمل أن يسددوا القرض إلى الفصل
−1دولا أو
0 سنقوم بتعيين هؤلاء المقترضين الذين لن يتمكنوا على الأرجح من سداد القرض.
لخص النتائج من هذا المثال البسيط. خذ نقطة
M(x1،x2) واستبدال إحداثيات النقطة في المعادلة المقابلة للخط
f(w،xi)=w0+w1xi1+w2xi2 ضع في اعتبارك ثلاثة خيارات:
- إذا كانت النقطة أسفل السطر ، فسنخصصها للفصل +1دولا ثم قيمة الوظيفة f(w،xi)=w0+w1xi1+w2xi2 سيكون إيجابيا من 0 إلى + infty . لذلك يمكننا أن نفترض أن احتمال سداد القرض هو في الداخل (0.5،1] . كلما زادت قيمة الوظيفة ، زاد الاحتمال.
- إذا كانت النقطة أعلى من السطر وقمنا بربطها بالفصل −1دولا أو 0 ، ثم ستكون قيمة الدالة سالبة من 0 إلى − infty . ثم سنفترض أن احتمال سداد الديون في الداخل [0،0.5) وكلما زادت قيمة معامل الوظيفة ، زادت ثقتنا.
- النقطة في خط مستقيم ، على الحدود بين فئتين. في هذه الحالة ، قيمة الوظيفة f(w،xi)=w0+w1xi1+w2xi2 سوف تكون متساوية 0 واحتمال سداد القرض يساوي
 .
.
الآن ، تخيل أنه ليس لدينا عاملان ، بل عشرات ، المقترضون ليسوا ثلاثة ، بل الآلاف. ثم بدلاً من خط مستقيم ، سيكون لدينا طائرة ذات معامل
m ومعاملات
w لن يتم أخذنا من السقف ، ولكن يتم سحبه وفقًا لجميع القواعد ، ولكن على أساس البيانات المتراكمة على المقترضين الذين عادوا أو لم يعودوا القرض. وفي الحقيقة ، مانع منكم ، إننا نختار الآن المقترضين بنسب معروفة بالفعل
w . في الواقع ، مهمة نموذج الانحدار اللوجستي هي تحديد المعلمات بدقة
w عندها تكون قيمة دالة الخسارة
Logistic Loss تميل إلى الحد الأدنى. ولكن كيف يتم حساب المتجه
vecw ، لا نزال نكتشف في القسم الخامس من المقال. في غضون ذلك ، نعود إلى الأرض الموعودة - إلى مصرفنا وعملائه الثلاثة.
شكرا للعمل
f(w،xi)=w0+w1xi1+w2xi2 نحن نعرف من الذي يمكن أن يحصل على قرض ، ومن يحتاج إلى الرفض. لكن لا يمكنك الذهاب إلى المدير بمثل هذه المعلومات ، لأنهم أرادوا الحصول على احتمال سداد القرض من كل مقترض منا. ما يجب القيام به الجواب بسيط - نحن بحاجة إلى تحويل الوظيفة بطريقة أو بأخرى
f(w،xi)=w0+w1xi1+w2xi2 قيمه تكمن في النطاق
(− infty،+ infty) على وظيفة تكمن قيمها في النطاق
[0،1] . وتوجد مثل هذه الوظيفة ، وتسمى
وظيفة الاستجابة اللوجستية أو تحويل السجل العكسي . اجتماع
sigma( vecwT vecxi)= frac11+e− vecwT vecxi
دعونا نلقي نظرة على الخطوات للحصول
على وظيفة الاستجابة اللوجستية . لاحظ أننا سنخطو في الاتجاه المعاكس ، أي نحن نفترض أننا نعرف قيمة الاحتمال ، والتي تكمن في النطاق من
0 إلى
1 ثم سنقوم "بتدوير" هذه القيمة على مجموعة كاملة من الأرقام من
− infty إلى
+ infty .
03. إخراج وظيفة الاستجابة اللوجستية
الخطوة 1. نقل قيم الاحتمالات إلى النطاق [0،+ infty)
في وقت التحول وظيفة
f(w،xi)=w0+w1xi1+w2xi2 لوظيفة الاستجابة اللوجستية sigma( vecwT vecxi)= frac11+e vecwT vecxi سنترك محلل الائتمان لدينا بمفرده ، وبدلاً من ذلك نذهب إلى مكاتب المراهنات. لا ، بالطبع ، لن نجعل رهانات ، كل ما يهمنا هو معنى التعبير ، على سبيل المثال ، فرصة من 4 إلى 1. الاحتمالات المألوفة لجميع اللاعبين الذين يراهنون هي نسبة "النجاحات" إلى "الإخفاقات". من حيث الاحتمالات ، الاحتمالات هي احتمال وقوع حدث مقسوم على احتمال عدم حدوث الحدث. نكتب الصيغة للحصول على فرصة لحدث ما
(احتمالات+) :
odds+= fracp+1−p+
حيث
p+ - احتمال وقوع حدث ،
(1−p+) - احتمال عدم وقوع حدث
على سبيل المثال ، إذا كان احتمال أن يكون هناك شاب شاب قوي وقادر على روح عالية ، يُطلق عليه "Veterok" ، سيهزم المرأة العجوز العجوز التي تحمل اسم "Matilda" في السباقات على قدم المساواة

، ثم فرص نجاح Veterka ستكون

إلى
1(0.8/(1−0.8)) والعكس بالعكس ، ومعرفة الفرص ، لن يكون من الصعب علينا حساب الاحتمال
p+ :
fracp+1−p+=4 mkern15mu Longrightarrow mkern15mup+=4(1−p+) mkern15mu Longrightarrow mkern15mu5p+=4 mkern15mu Longrightarrow mkern15mup+=0.8دولاوهكذا ، تعلمنا "ترجمة" الاحتمال إلى احتمالات تأخذ قيمًا منها
0 إلى
+ infty . دعنا نأخذ خطوة أخرى ونتعلم كيفية "ترجمة" الاحتمال إلى سطر الرقم بالكامل من
− infty إلى
+ infty .
الخطوة 2. نترجم قيم الاحتمالات إلى المدى (− infty،+ infty)
هذه الخطوة بسيطة جدًا - نعرض الاحتمالات بناءً على رقم Euler
e واحصل على:
f(w،xi)= vecwT vecx=ln(احتمالات+)
الآن نحن نعرف أنه إذا
p+=0.8دولا ثم احسب القيمة
f(w،xi) سيكون الأمر بسيطًا جدًا ، علاوة على ذلك ، يجب أن يكون إيجابيًا:
f(w،xi)=ln(احتمالات+)=ln(0.8/0.2)=ln(4) approx+1.38629 . هكذا هو.
من أجل الفضول ، نتحقق من ذلك
p+=0.2دولا ثم نتوقع أن نرى قيمة سلبية
f(w،xi) . نتحقق من:
f(w،xi)=ln(0.2/0.8)=ln(0.25) approx−1.38629 . كل الحق.
الآن نحن نعرف كيفية ترجمة قيمة الاحتمال من
0 إلى
1 على خط العدد كله من
− infty إلى
+ infty . في الخطوة التالية ، سنفعل العكس.
في غضون ذلك ، نلاحظ أنه وفقا لقواعد اللوغاريتم ، معرفة قيمة الوظيفة
f(w،xi) ، يمكنك حساب الاحتمالات:
odds+=ef(w،xi)=e vecwT vecx
هذه الطريقة لتحديد الفرص ستكون مفيدة في الخطوة التالية.
الخطوة 3. نشتق صيغة لتحديد p+
لذلك تعلمنا ، مع العلم
p+ العثور على قيم الوظيفة
f(w،xi) . ومع ذلك ، في الواقع ، نحن بحاجة إلى كل شيء عكس ذلك تمامًا - معرفة القيمة
f(w،xi) لتجد
p+ . للقيام بذلك ، ننتقل إلى مفهوم مثل الوظيفة العكسية للفرص ، وفقًا لما يلي:
p+= fracodds+1+odds+
في المقالة ، لن نستمد الصيغة أعلاه ، ولكن تحقق من الأرقام الموجودة في المثال أعلاه. نحن نعلم أنه مع احتمالات من 4 إلى 1 (

) ، احتمال وقوع حدث هو 0.8 (
p+=0.8دولا ). دعنا نجعل بديلا:
p+= frac41+4=0.8دولا . هذا يتزامن مع حساباتنا التي أجريت في وقت سابق. نحن نمضي قدما.
في الخطوة الأخيرة ، استنتجنا ذلك
odds+=e vecwT vecx ، مما يعني أنه يمكنك إجراء استبدال في الوظيفة العكسية للاحتمالات. نحصل على:
p+= frace vecwT vecx1+e vecwT vecx
اقسم البسط والمقام على
e vecwT vecx ثم:
p+= frac11+e− vecwT vecx= sigma( vecwT vecx)
لكل رجل إطفاء ، للتأكد من أننا لم نرتكب أي خطأ في أي مكان ، سنقوم بإجراء فحص صغير آخر. في الخطوة 2 ، نحن من أجل
p+=0.8دولا قرر ذلك
f(w،xi) approx+1.38629 . ثم ، استبدال القيمة
f(w،xi) في وظيفة الاستجابة اللوجستية ، نتوقع الحصول عليها
p+=0.8دولا . بديلاً واحصل على:
p+= frac11+e−1.38629=0.8دولاتهانينا ، عزيزي القارئ ، قمنا بتطوير واختبار وظيفة الاستجابة اللوجستية. دعونا نلقي نظرة على الرسم البياني وظيفة.
الرسم البياني 3 "وظيفة الاستجابة اللوجستية"

رمز للتخطيط import math def logit (f): return 1/(1+math.exp(-f)) f = np.arange(-7,7,0.05) p = [] for i in f: p.append(logit(i)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(f, p, color = 'grey', label = '$ 1 / (1+e^{-w^Tx_i})$') plt.xlabel('$f(w,x_i) = w^Tx_i$', size = 16) plt.ylabel('$p_{i+}$', size = 16) plt.legend(prop = {'size': 14}) plt.show()
في الأدب ، يمكنك أيضًا العثور على اسم هذه الوظيفة كدالة
السيني . يوضح الرسم البياني بوضوح أن التغيير الرئيسي في احتمال انتماء كائن إلى فئة ما يحدث في نطاق صغير نسبيًا
f(w،xi) في مكان ما من
−4دولا إلى
+4 .
أقترح العودة إلى محلل الائتمان لدينا ومساعدته على حساب احتمال سداد القروض ، وإلا فإنه يخاطر بالترك دون مكافأة :)
الجدول 2 "المقترضون المحتملون"
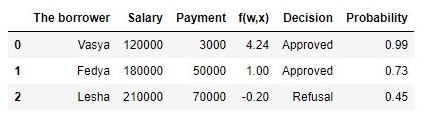
رمز لتوليد الجدول proba = [] for i in df['f(w,x)']: proba.append(round(logit(i),2)) df['Probability'] = proba df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision', 'Probability']]
لذلك ، قررنا احتمال سداد القرض. الكل في الكل ، يبدو أن هذا صحيح.
في الواقع ، فإن احتمال حصول Vasya براتب 120،000 سيكون قادرًا على إعطاء 3.000 شهريًا للبنك قريب من 100٪. بالمناسبة ، يجب أن نفهم أن البنك يمكن أن يقدم قرضًا ليشه أيضًا إذا كانت سياسة البنك تنص ، على سبيل المثال ، على إقراض العملاء باحتمالية سداد القرض بأكثر من 0.3 ، على سبيل المثال. فقط في هذه الحالة ، سيقوم البنك بتكوين احتياطي أكبر للخسائر المحتملة.
وتجدر الإشارة أيضًا إلى أن نسبة المرتب إلى دفع ما لا يقل عن 3 وبهامش قدره 5.000 تم أخذها من السقف. لذلك ، لم نتمكن من استخدام ناقل الوزن في شكله الأصلي
vecw=(−5000،1،−3) . كنا بحاجة إلى تقليل المعاملات بشكل كبير ، وفي هذه الحالة قمنا بتقسيم كل معامل على 25000 ، وهذا هو ، في الواقع ، قمنا بتعديل النتيجة. ولكن تم ذلك عن قصد لتبسيط فهم المواد في المرحلة الأولية. في الحياة ، لا نحتاج إلى اختراع المعاملات وضبطها ، ولكن للعثور عليها. فقط في الأقسام التالية من المقالة ، سنشتق المعادلات التي يتم تحديد المعلمات بها
vecw .
04. طريقة المربعات الصغرى لتحديد متجه الأوزان vecw في وظيفة الاستجابة اللوجستية
نحن نعرف بالفعل هذه الطريقة لاختيار ناقلات الوزن
vecw كأسلوب
المربعات الصغرى (OLS) ، وفي الواقع ، لماذا لا نستخدمها في مشاكل التصنيف الثنائي إذن؟ في الواقع ، لا يوجد شيء يمنع استخدام
الشركات متعددة الجنسيات ، فقط هذه الطريقة في مشاكل التصنيف تعطي نتائج أقل دقة من
الخسارة اللوجستية . هناك مبرر نظري لذلك. لنبدأ بالنظر إلى مثال بسيط واحد.
لنفترض أن موديلاتنا (باستخدام
MSE و
Logistic Loss ) قد بدأت بالفعل في اختيار ناقل الوزن
vecw وتوقفنا عن الحساب في بعض الخطوات. لا يهم ، في المنتصف ، في النهاية أو في البداية ، الشيء الرئيسي هو أن لدينا بالفعل بعض قيم متجه الأوزان ونفترض ، في هذه الخطوة ، متجه الأوزان
vecw لكلا النموذجين ليس لديهم اختلافات. ثم نأخذ الأوزان التي تم الحصول عليها ونستبدلها في
وظيفة الاستجابة اللوجستية (
frac11+e− vecwT vecx ) لبعض الأشياء التي تنتمي إلى الفصل
+1دولا . سنقوم بالتحقيق في حالتين عندما يكون نموذجنا مخطئًا إلى حد كبير والعكس صحيح - وفقًا لمتجه الأوزان المحدد - فالنموذج واثق تمامًا من أن الكائن ينتمي إلى الفصل
+1دولا . دعونا نرى ما هي الغرامات التي سيتم إصدارها عند استخدام
الشركات متعددة الجنسيات والخسارة اللوجستية .
رمز لحساب الغرامات اعتمادا على وظيفة الخسارة المستخدمة الحالة مع خطأ فادح - يصنف النموذج الكائن
+1دولا مع احتمال 0.01
العقوبة عند استخدام
OLS هي:

العقوبة عند استخدام
Logistic Loss هي:
LogLoss=loge(1+e−yf(w،x))=loge(1+e−1(−4.595...)) approx4.605حالة مع اليقين القوي - يصنف النموذج الكائن
+1دولا مع احتمال 0.99
العقوبة عند استخدام
OLS هي:

العقوبة عند استخدام
Logistic Loss هي:
LogLoss=loge(1+e−4.595...) approx0.01يوضح هذا المثال بشكل جيد أنه مع وجود خطأ فادح ، فإن وظيفة
Log Loss loss تغني النموذج أكثر بكثير من
MSE . دعنا الآن نفهم ما هي المتطلبات النظرية لاستخدام دالة
Loss Log Log في مشاكل التصنيف.
05. طريقة المصداقية القصوى والانحدار اللوجستي
كما وعدنا في البداية ، تزخر المقالة بأمثلة بسيطة. في الاستوديو ، مثال آخر والضيوف القدامى هم المقترضون من البنك: فازيا ، فيديا وليشا.
بالنسبة لكل رجل إطفاء ، قبل وضع مثال ، اسمحوا لي أن أذكرك بأننا في الحياة نتعامل مع عينة تدريب من آلاف أو ملايين الأشياء بعشرات أو مئات من العلامات. ومع ذلك ، هنا يتم أخذ الأرقام بحيث تناسب بسهولة في رأس datasintest المبتدئ.
نعود على سبيل المثال. تخيل أن مدير البنك قرر إعطاء قرض لجميع المحتاجين ، على الرغم من أن الخوارزمية اقترحت عدم إعطائها ليشا. ومضى الكثير من الوقت وأصبحنا ندرك أي من الأبطال الثلاثة سدد القرض ومن لم يفعل. ما كان متوقعًا: سدد Vasya و Fedya القرض ، لكن أليكس لم يفعل. الآن دعنا نتخيل أن هذه النتيجة ستكون عينة تدريب جديدة بالنسبة لنا ، وفي الوقت نفسه ، يبدو أن جميع البيانات المتعلقة بالعوامل المؤثرة في احتمال سداد القرض (راتب المقترض ، مبلغ الدفعة الشهرية) قد اختفت. ثم ، حدسيًا ، يمكننا أن نفترض أن كل مقترض ثالث لا يُرجع قرضًا إلى البنك ، أو بمعنى آخر ، احتمال إعادة قرض من قبل المقترض التالي
p= frac23 . هناك دليل نظري لهذا الافتراض الحدسي ويستند إلى
طريقة الاحتمالية القصوى ، والتي يشار إليها غالبًا في الأدبيات على أنها
مبدأ الاحتمال الأقصى .
أولاً ، تعرف على الجهاز المفاهيمي.
إن احتمال وجود
عينة هو احتمال الحصول على مثل هذه العينة ، والحصول على مثل هذه الملاحظات / النتائج بدقة ، أي نتاج احتمالات الحصول على كل من نتائج العينة (على سبيل المثال ، تم سداد قرض Vasya و Feday و Lesha في نفس الوقت أو عدم سداده).
تقوم دالة الاحتمالية بربط احتمالية العينة بقيم معلمات التوزيع.
في حالتنا ، تكون عينة التدريب عبارة عن مخطط برنولي معمم يأخذ فيه المتغير العشوائي قيمتين فقط:
1 أو
0 . لذلك ، يمكن كتابة احتمال العينة كدالة لاحتمال المعلمة
ع على النحو التالي:
P( mkern5mu vecy mkern5mu| mkern5mup)= prod limit3i=1pyi(1−p)(1−yi) mkern5mu= mkern5mup1(1−p)1−1 centerdotp1(1−p)1−1 centerdotp0(1−p)1−0 mkern5mu== mkern5mup centerdotp centerdot(1−p) mkern5mu= mkern5mup2(1−p)يمكن تفسير السجل أعلاه على النحو التالي. الاحتمال المشترك أن فاسيا و Fedya سداد القرض يساوي
p centerdotp=p2 ، احتمال أن أليكس لن يسدد القرض
1−p (لأنه لم يكن سداد القرض) ، وبالتالي ، فإن الاحتمال المشترك لجميع الأحداث الثلاثة هو
p2(1−p) .
—
.
p ,
P(→y|p)=p2(1−p) .
– , ? , – , , . , , . , , , , – , . , , .
, , . , . , —
. ? ,
P(→y|p) , ,
p ,
P(→y|p) . ( ), — .
, , , .
:
logP(→y|p)=logp2(1−p)=2logp+log(1−p)p :
∂logP(→y|p)∂p=∂∂p(2logp+log(1−p))=2p−11−p, — :
2p−11−p=0⟹2p=11−p⟹2(1−p)=p⟹p=23,
p=23 .
, ? , , . - ,
23 , : . , . ,
23 .
:
from functools import reduce def likelihood(y,p): line_true_proba = [] for i in range(len(y)): ltp_i = p[i]**y[i]*(1-p[i])**(1-y[i]) line_true_proba.append(ltp_i) likelihood = [] return reduce(lambda a, b: a*b, line_true_proba) y = [1.0,1.0,0.0] p_log_response = df['Probability'] const = 2.0/3.0 p_const = [const, const, const] print ' p=2/3:', round(likelihood(y,p_const),3) print '****************************************************************************************************' print ' p:', round(likelihood(y,p_log_response),3)
, . ? , . , , , 3- , .
,
, - , , , , 0.99, 0.99 0.01 . ,
1 , , -, , , -, . , ( ) , . , . ? , . 2.5% , — 27,8%. 2 « » , , , . , ,
f(w,x)=w0+w1x1+w2x2 : 4.24 1.0 . , , , . , .
w , , ,
w , ,
w , — :)
.
→w , .
,
w :
1. , ( ) , — .
f(w,x)=→wTX , ()
+1 −1 0 (, ).
f(w,x)=w0+w1x1+w2x2 .
2.
- p+=11+e−→wT→x=σ(→wT→x) +1 .
3.
, ,
p ( ) 1
(1–p) – 0.
4. ,
, . , , . —
p ,
w .
→w , .
5. ,
. .
:)
,
Logistic Loss . , ,
+1 0 −1 . , .
1. +1 0
, ,
w , :
P(→y|p)=3∏i=1pyi(1−p)(1−yi)pi —
p+=11+e−→wT→x=σ(→wT→x) →w:
P(→y|σ(→wTX))=n∏i=1σ(→wT→xi)yi(1−σ(→wT→xi)(1−yi)→max
, , , . 4 , :
1. yi=+1 (.. +1),
σ(→wTX)) +1 0.9, :
0.91⋅(1−0.9)(1−1)=0.91⋅0.10=0.92. yi=+1 ,
σ(→wTX))=0.1 , :
0.11⋅(1−0.1)(1−1)=0.11⋅0.90=0.13. yi=0 ,
σ(→wTX))=0.1 , :
0.10⋅(1−0.1)(1−0)=0.10⋅0.91=0.94. yi=0 ,
σ(→wTX))=0.9 , :
0.90⋅(1−0.9)(1−0)=0.90⋅0.11=0.1, 1 3 —
+1 .
,
+1 w , . , ,
w . :
.
Llog(X,→y,→w)=n∑i=1(−yilogeσ(→wT→xi)−(1−yi)loge(1−σ(→wT→xi)))→min
,
,
+ − . , ,
− , .
, , —
Logistic Loss :
+1 0 .
, ,
, , ,
w . , , , , , .
2. +1 −1
,
1 0 ,
Logistic Loss , . .
«..., ...» . ,
i -
+1 ,
p ,
−1 ,
(1−p) . :
P(→y|σ(→wTX))=n∏i=1σ(→wT→xi)[yi=+1](1−σ(→wT→xi)[yi=−1])→max
. 4 :
1. yi=+1 σ(→wT→xi)=0.9 , «»
0.92. yi=+1 σ(→wT→xi)=0.1 , «»
0.13. yi=−1 σ(→wT→xi)=0.1 , «»
1−0.1=0.94. yi=−1 σ(→wT→xi)=0.9 , «»
1−0.9=0.1, 1 3 , ,
, . , . , , .
Llog(X,→y,→w)=n∑i=1(−[yi=+1]logeσ(→wT→xi)−[yi=−1]loge(1−σ(→wT→xi)))→min
σ(→wT→xi) 11+e−→wT→xi :
Llog(X,→y,→w)=n∑i=1(−[yi=+1]loge(11+e−→wT→xi)−[yi=−1]loge(1−11+e−→wT→xi))→min
, :
Llog(X,→y,→w)=n∑i=1(−[yi=+1]loge(11+e−→wT→xi)−[yi=−1]loge(11+e→wT→xi))→min
«..., ...» . ,
yi +1 , , ,
e −→wT→xi ,
−1 , $e$
+→wT→xi . — :
−yi→wT→xi .
:
Llog(X,→y,→w)=n∑i=1−loge(11+e−yi→wT→xi)→min
, "
− " () , :
Llog(X,→y,→w)=n∑i=1loge(1+e−yi→wT→xi)→min
logistic Loss , :
+1 −1 .
, .
← — « »1.
1) / . , . – 2- . – .: , 1986 ( )
2) / .. — 9- . — .: , 2003
3) / .. — : , 2007
4) -: / . ., . . — 2- . — -: , 2013
5) Data Science / — -: , 2017
6) Data Science / ., . — -: , 2018
2. , ()
1)
,2)
,3)
. ODS, Yury Kashnitsky4)
4, ( 47 )5)
,3. -
1)
2)
3)
4)
5)
6)
7)
8)
e ?9)