عشية بدء الدورة "الرياضيات لعلوم البيانات. دورة متقدمة " أجرينا ندوة عبر الإنترنت مفتوحة حول موضوع" طرق تحليل الانحدار في علوم البيانات ". تعرّفنا على مفهوم الانحدارات الخطية ، ودرسنا أين وكيف يمكن تطبيقها في الممارسة العملية ، وتعلمنا أيضًا موضوعات وأقسام التحليل الرياضي والجبر الخطي ونظرية الاحتمالات المستخدمة في هذا المجال. محاضر - بيتر لوكيانشنكو ، محاضر في المدرسة العليا للاقتصاد ، رئيس مشاريع التكنولوجيا
إذا تحدثنا عن الرياضيات في سياق علوم البيانات ، فيمكننا استبعاد المشكلات الثلاث التي يتم حلها بشكل متكرر (على الرغم من وجود المزيد من المشكلات بالطبع):

دعونا نتحدث عن هذه المهام بمزيد من التفاصيل:
- مهمة تحليل الانحدار أو تحديد التبعيات (عندما يكون لدينا مجموعة معينة من الملاحظات). في الرسم البياني أعلاه ، يمكنك أن ترى أن هناك متغيرًا معينًا x ومتغيرًا معينًا y ، ونلاحظ قيم y بالنسبة إلى x معين. نحن نعرف هذه النقاط ونعرف إحداثياتها ، ونعلم أيضًا أن x تؤثر بطريقة ما على y ، أي أن هذين المتغيرين يعتمدان على بعضهما البعض. بطبيعة الحال ، نريد حساب معادلة التبعية الخاصة بهم - لهذا نستخدم نموذج الانحدار الخطي للزوج الكلاسيكي ، عندما يُفترض أن اعتمادهم يمكن وصفه بخط مستقيم معين. وفقًا لذلك ، يتم تحديد معاملات الخط المستقيم لتقليل الخطأ في وصف البيانات. وفقط على نوع الخطأ (مقياس الجودة) الذي سيتم اختياره ، تعتمد النتيجة الفعلية لبناء الانحدار الخطي.
- مهمة أخرى من تحليل البيانات هي نظم التوصية . هذا عندما نقول أن هناك ، على سبيل المثال ، متاجر على الإنترنت ، لديهم مجموعة معينة من السلع ، ويقوم شخص ما بالشراء. استنادًا إلى هذه المعلومات ، من الممكن تقديم وصف لهذا الشخص في مساحة المتجه ، وبناء هذا المتجه ، أنشئ اعتمادًا رياضيًا على الاحتمال الذي سيشتري به هذا المنتج أو ذاك مع العلم عن مشترياته السابقة. وفقًا لذلك ، نحن نتحدث عن التصنيف عندما نقوم بتصنيف المشترين المحتملين وفقًا للمبادئ: "شراء - عدم شراء" ، "اهتمام - غير مهتم" ، وما إلى ذلك. هناك طرق مختلفة: تعتمد على المستخدم وعلى أساس العنصر.
- المجال الثالث هو رؤية الكمبيوتر . في سياق هذه المهمة ، نحاول تحديد مكان وجود الكائن الذي يهمنا. هذا في الواقع حل لمشكلة تقليل الأخطاء عن طريق تحديد وحدات بكسل محددة تشكل صورة الكائن.
في جميع المشكلات الثلاث ، هناك التحسين وتقليل الأخطاء ووجود نموذج أو آخر يصف اعتماد المتغيرات. في الوقت نفسه ، يوجد داخل كل منها تمثيل للبيانات المتحللة في وصف متجه. في مقالتنا ، سنولي اهتمامًا خاصًا للقسم الذي يؤثر على
نماذج الانحدار .
لقد ذكرنا بالفعل أن هناك مجموعة معينة من أزواج البيانات: X و Y. ونعرف القيم التي تأخذها Y فيما يتعلق X. إذا كان X هو الوقت ، فسوف نحصل على نموذج سلسلة زمنية يكون فيه Y ، مثلاً ، سعر النفط وفي الوقت نفسه ، فإن سعر صرف الروبل مقابل الدولار ، و X هو فترة زمنية معينة من 2014 إلى 2018:
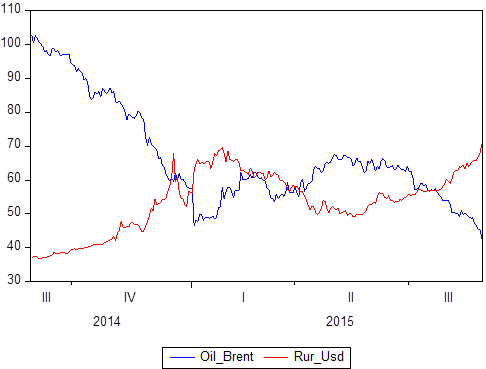
إذا قمت بالبناء بيانيا ، فمن الواضح أن هذه السلاسل الزمنية اثنين مترابطة. بعد تعريف مفهوم الارتباط ، يمكنك حساب درجة التبعية ، ومن ثم ، إذا كنت تعرف أن بعض القيم مرتبطة تمامًا (الارتباط هو 1 أو -1) ، يمكنك استخدام هذا إما لمهام التنبؤ أو مهام الوصف.
النظر في الرسم التوضيحي التالي:
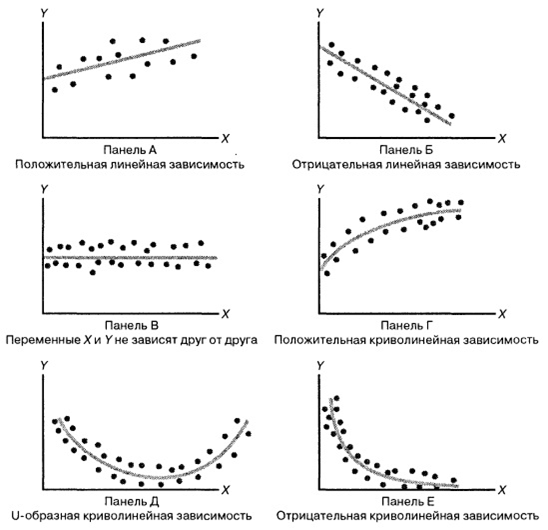
الجزء الأكثر صعوبة في تشكيل نموذج الانحدار هو
وضع بعض الوظائف المحددة في ذاكرته في البداية . على سبيل المثال ، بالنسبة للشكل A ، تكون Y = kX + b ، أما بالنسبة إلى B فهي Y = -kX + b ، في الشكل C ، تساوي "اللعبة" بعض الأرقام ، وغالبًا ما يعتمد الرسم البياني في الشكل D على الجذر من " X "، عند قاعدة D ، وربما قطع مكافئ ، وقاعدة E - غلو.
اتضح
أننا نختار نموذجًا من الاعتماد على البيانات ، وأنواع التبعية بين المتغيرات العشوائية مختلفة. كل شيء ليس واضحًا للغاية ، لأنه حتى في هذه الرسومات البسيطة نرى تبعيات مختلفة. باختيار علاقة محددة ، يمكننا استخدام طرق الانحدار لمعايرة النموذج.
تعتمد جودة تنبؤاتك على النموذج الذي تختاره . إذا ركزنا على نماذج الانحدار الخطي ، فإننا نفترض أن هناك مجموعة معينة من القيم الحقيقية:

يوضح الشكل القيم الأربعة الملاحظة X1 و X2 و X2 و X4. بالنسبة لكل من X ، فإن قيمة Y معروفة (في حالتنا ، هذه هي النقاط: P1 ، P2 ، P3 ، P4). هذه هي النقاط التي نلاحظها بالفعل على البيانات. وبالتالي ، تلقينا مجموعة بيانات معينة. ولسبب ما ، قررنا أن الانحدار الخطي يصف بشكل أفضل العلاقة بين X واللاعب. علاوة على ذلك ، فإن السؤال برمته هو كيفية بناء معادلة الخط المستقيم Y = b
1 + b
2 X ، حيث b
2 هي معامل الميل ، b
1 هي معامل التقاطع. والسؤال برمته هو تحديد b
2 و b
1 بحيث يصف هذا الخط المستقيم العلاقة بين هذه المتغيرات بدقة قدر الإمكان.
النقاط R
1 و R
2 و R
3 و R
4 هي القيم التي يعطيها نموذجنا بقيم X. ماذا يحدث؟ النقاط P هي نقاط نلاحظها بالفعل (تم جمعها فعليًا) ، والنقاط R هي نقاط نلاحظها في نموذجنا (تلك التي ينتجها). ما يلي هو منطق بشري بسيط بجنون:
سيتم اعتبار النموذج نوعيًا إذا وفقط إذا كانت النقاط R قريبة من النقاط P قدر الإمكان .
إذا قمنا ببناء المسافة بين هذه النقاط لنفس "X" (P
1 - R
1 ، P
2 - R
2 ، إلخ) ، فسنحصل على ما يسمى أخطاء الانحدار الخطي. نحصل على الانحرافات في الانحدار الخطي ، وتسمى هذه الانحرافات U
1 ، U
2 ، U
3 ... U
n . ويمكن أن تكون هذه الأخطاء إما زائد أو ناقص (يمكننا المبالغة في تقدير أو التقليل من شأن). لمقارنة هذه الانحرافات ، يجب تحليلها. يتم استخدام طريقة كبيرة وجميلة للغاية هنا - التربيع (تربيع "يقتل" العلامة). ويسمى مجموع المربعات من جميع الانحرافات في الإحصاءات الرياضية آر إس إس (مجموع المتبقية من المربعات). بتقليل RSS بمقدار b
1 وتقليل RSS بمقدار b
2 ، نحصل على المعاملات المثالية المشتقة بالفعل
من طريقة المربعات الصغرى .
بعد أن قمنا ببناء الانحدار ، حددنا المعاملات المثلى b
1 و b
2 ، ولدينا معادلة الانحدار ، والمشاكل لا تنتهي عند هذا الحد ، وتستمر المشكلة في التطور. والحقيقة هي أنه إذا تم وضع علامة الانحدار نفسه على رسم بياني واحد ، فإن كل القيم التي لدينا ، وكذلك متوسط قيم "الألعاب" ، يمكن توضيح مجموع الأخطاء المربعة.
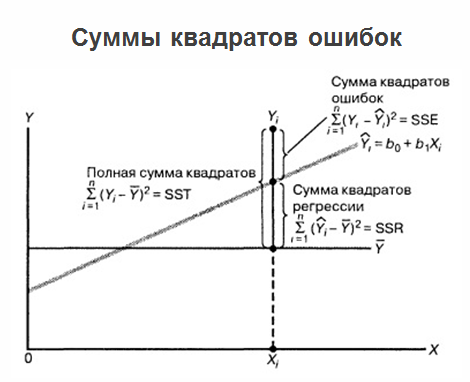
في الوقت نفسه ، من المفيد عرض أخطاء تنبؤ الانحدار فيما يتعلق بالمتغير X. انظر الشكل أدناه:

لقد حصلنا على نوع من الانحدار واستخلصنا البيانات الحقيقية. وصلنا المسافة من كل قيمة حقيقية إلى الانحدار. وقمنا برسمها بالنسبة إلى القيمة الصفرية للقيم المقابلة لـ X. وفي الشكل أعلاه ، نرى صورة سيئة حقًا:
الأخطاء تعتمد على X. يتم التعبير بوضوح عن اعتماد الارتباط:
كلما كانت المسافة "X" التي نتحرك بها ، زادت أهمية الأخطاء . هذا سيء جدا يشير وجود الارتباط في هذه الحالة إلى أننا اتخذنا عن طريق الخطأ نموذج الانحدار ، وكان هناك بعض المعايير التي "لم نفكر فيها" أو لم نغفل عنها. بعد كل شيء ، إذا تم وضع جميع المتغيرات داخل النموذج ، يجب أن تكون الأخطاء عشوائية تمامًا ويجب ألا تعتمد على العوامل التي تساويها.
يجب أن تكون الأخطاء مع نفس توزيع الاحتمالات ، وإلا ستكون تنبؤاتك خاطئة. إذا كنت قد رسمت أخطاء النموذج الخاص بك على متن الطائرة وقابلت مثلثًا متباعدًا ، فمن الأفضل أن تبدأ كل شيء من نقطة الصفر وإعادة فرز النموذج بالكامل.
من خلال تحليل الأخطاء ، يمكنك حتى أن تفهم على الفور المكان الذي أخطأت فيه ، ونوع الخطأ الذي ارتكبوه. وهنا لا يمكننا أن نذكر نظرية غاوس - ماركوف:

تحدد النظرية الشروط التي تكون التقديرات التي تم الحصول عليها باستخدام طريقة المربعات الصغرى هي الأفضل والمتسقة والفعالة في فئة التقديرات الخطية غير المتحيزة.
الاستنتاج يمكن استخلاصه على النحو التالي: الآن نحن نفهم أن
مجال بناء نموذج الانحدار هو ، إلى حد ما ، تتويجا من وجهة نظر الرياضيات ، لأنه يدمج جميع الأقسام الممكنة في وقت واحد ، والتي يمكن أن تكون مفيدة في تحليل البيانات ، على سبيل المثال:
- الجبر الخطي مع طرق تمثيل البيانات ؛
- التحليل الرياضي مع نظرية التحسين ووسائل تحليل الوظائف ؛
- نظرية الاحتمالات بوسائل لوصف الأحداث العشوائية والكميات ونمذجة العلاقة بين المتغيرات.
الزملاء ، أقترح كل ذلك ، لا يقتصر على قراءة ومشاهدة الندوة عبر الويب بأكملها . لم تتضمن المقالة لحظات متعلقة بالبرمجة الخطية ، والتحسين في نماذج الانحدار ، وغيرها من التفاصيل التي قد تكون مفيدة لك.