Die Balken von Zhenya und Luke - ein Multiplikatorwerkzeug des späten 19. Jahrhunderts
Dieser Artikel widmet sich einem Hilfsmittel für die Multiplikation, Stangen, die 1885 vom Eisenbahningenieur Eugene (sic) und einem Mitarbeiter des Pariser Kunst- und Handwerksmuseums Eduard Luke (sic) vorgeschlagen wurden [1].Die Transliteration der Namen der Erfinder unterscheidet sich in verschiedenen Quellen, daher zitiere ich eine Reihe von Optionen (die ich googeln musste) in lateinischer Sprache: Genaille (Zhenya, Zhenya, Zhenya, Zhenail), Lucas (Luca, Luc, Lucas).Die Bars von Eugene und Luke waren bequemer als die Zauberstäbe von Neper, die ihnen vorausgingen, und konnten durchaus mit den modernen Bars von Joffe (nach dem Slonim-Theorem) konkurrieren.Es gibt praktisch keine Informationen zu diesem Produkt in Runet. Neulich habe ich plötzlich einen Artikel auf Deutsch gegoogelt, der mir geholfen hat, in das Prinzip der Bars einzusteigen. Nicht auf den Artikel beschränkt, habe ich das Erscheinungsbild der Arbeitsfläche der Balken aus den Bildern mit Blick auf einige von ihnen wiederhergestellt und mich auf das Prinzip ihrer Wirkung konzentriert. Die später an derselben Stelle gefundenen Materialien bestätigten die Richtigkeit meiner Rekonstruktion.Zweck des Schreibens eines Artikels
Dieser Artikel richtet sich an diejenigen, die sich wie ich für die Geschichte der Computertechnologie interessieren.In RuNet konnte ich an den Bars von Zhenai und Luc (Genaille & Lucas) nichts Sinnvolles finden. Die deutschsprachige Website , auf der ein Artikel mit seiner Beschreibung gefunden wurde, half dabei , das Funktionsprinzip dieses Zählwerkzeugs zu verstehen .Warum Habr als Platzierung des Artikels ausgewählt wird
Der Artikel ist zwar uralt, aber immer noch Computertechnologie gewidmet. Daher ist für Habr ein Thema geeignet.Habr ist gut indiziert, und ich möchte, dass es jedem, der an diesem Zählwerkzeug interessiert ist, leicht fällt, Informationen darüber zu finden.Produktbeschreibung und Funktion
Die Balken von Zhenya und Luke sowie andere ähnliche Produkte sind so konzipiert, dass schnell das Produkt einer mehrstelligen Nummer mit einer einstelligen Nummer erhalten wird.Das Multiplikationswerkzeug besteht aus 11 Balken. Jeder Balken verfügt über eine Digitalwaage, auf der sich das Ergebnis befindet. Die Skala ist in 8 Teile unterteilt, was einer Multiplikation mit Zahlen von 2 bis 9 entspricht. Ein Balken dient als Hinweis - die Teile der Skala sind mit den Zahlen 2 ... 9 signiert - dies sind die Werte eines einstelligen Faktors, und die Skala selbst dient zum Lesen der höchsten Ebene der Arbeit. Die verbleibenden Balken sind von 0 bis 9 nummeriert und dienen zum Multiplizieren der entsprechenden Zahlen. In ihnen befindet sich neben der Skala ein Dreieck, dessen rechte Seite die digitale Skala nach links begrenzt, und der linke Scheitelpunkt befindet sich am linken Rand des Balkens. Wenn die Balken gestapelt sind, zeigt dies die Position der nächsten Entladung des Produkts auf dem nächsten Balken an.
Eine kleine Analyse: Es ist leicht zu erkennen, dass jeder Teil der Skala jedes Balkens mit einer Ziffer beginnt, die dem Wert der Kategorie der Einheiten des Produkts der Nummer des Balkens durch die Teilenummer der Skala entspricht. In Takt 8 beginnt beispielsweise Fragment 9 mit der Nummer 2 (8 * 9 = 72). Die Länge jedes Teils der Skala entspricht dem Wert eines einstelligen Faktors - was natürlich ist, weil Wenn eine beliebige Zahl mit einem einstelligen Faktor multipliziert wird, ist die höchste Ziffer des Produkts kleiner als dieser Faktor, d. h. Wenn sie beispielsweise mit 5 multipliziert werden, überschreitet der auf die nächste Ziffer übertragene Wert niemals 4, wenn sie mit 9, 8 usw. multipliziert werden. Der Betrag der Ziffernverschiebung vom Beginn der Skala nach unten ist gleich dem Wert der Übertragung vom niedrigstwertigen Bit. Es stellt sich heraus, dass die Position des linken Scheitelpunkts des schwarzen Dreiecks dem Wert der zweiten Ziffer des Produkts der Balkennummer durch einen einstelligen Faktor entspricht, zu dem eine Zahl hinzugefügt wird.von der niedrigen Ordnung übertragen.Um eine mehrstellige Zahl mit einer einstelligen Zahl zu multiplizieren, müssen Sie die Balken zusammen mit den Zahlen addieren, die den Ziffern der Ziffern entsprechen, und links einen Balken mit einem Hinweis anhängen. Dann ist es in jedem Teil der Skala möglich, die Produkte dieser Nummer anhand der entsprechenden einstelligen Nummer zu betrachten. Die Entladung von Einheiten ist die erste Ziffer des gewünschten Teils der Skala, und jede nachfolgende Entladung zeigt uns den linken Scheitelpunkt des Dreiecks an, dessen rechte Seite als linker Rand der Zelle der vorherigen Entladung dient.Nehmen Sie zum Beispiel die Nummer 7519. Stellen Sie einen Balken mit einem Hinweis und den Balken 7, 5, 1 und 9 zusammen. Das Diagramm ist in der folgenden Abbildung dargestellt.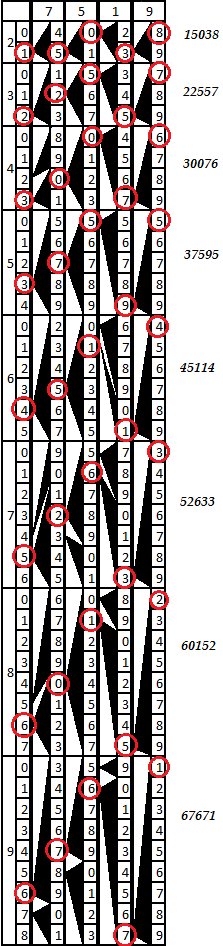
In jedem Teil der resultierenden Tabelle können Sie nach den Dreieckszeichen die Kategorien von Werken von rechts nach links verfolgen.Das Schema ist klarer als alle Wörter. Folgen wir zum Beispiel der Multiplikation mit 9. Am Anfang des neunten (letzten) Teils der Skala des rechten Balkens sehen wir die Nummer 1. Das Dreieck zeigt die Nummer 7 des benachbarten Balkens an, von dort zeigt das Dreieck 6, dann - 7 und noch weiter - die Nummer 6 auf der Bar-Tip-Skala. ZU. wir erhalten den Wert 67671 = 7519 * 9.Andere Werke werden ebenfalls verfolgt. Es ist leicht zu überprüfen, ob sie korrekt sind. Daher ist das Werkzeug für den Einsatz geeignet.Spekulationen zum Thema Erscheinung
Apokin I.A., Maistrov L.E. In der Quelle [1] schreiben sie, dass auf den digitalen Balken alle vier Oberflächen funktionierten. Es ist logisch anzunehmen, dass Oberflächen zum Duplizieren von Skalen verwendet wurden, was zum Kompilieren mehrstelliger Zahlen mit mehreren Vorkommen derselben Ziffer erforderlich ist.Angenommen, basierend auf der Anzahl der Seiten des Balkens befanden sich vier vollständige Skalensätze auf 10 Balken.Angenommen, die Skalen auf den Balken müssen so angeordnet sein, dass Sie mit den Balken eine beliebige vierstellige Zahl eingeben können.Sie finden viele Optionen zum Platzieren von Arbeitsskalen auf Stangen, die diese Anforderung erfüllen. Nehmen Sie zum Beispiel zwei Balken von fünf Typen mit Flächen:0,1,2,3;2,3,4,5;4,5,6,7;6,7,8,9;0,1,8,9.Eine andere Möglichkeit, vier Flächen zu verwenden, besteht darin, eine Skala in Teilen darauf zu platzieren und so die Länge der Stange zu verringern. Diese Option ist weniger bequem zu verwenden, weil erlaubt nicht, alle Werke auf einmal zu sehen.Die Skala besteht aus 8 Teilen mit einer Länge von 2 bis 9. Sammeln Sie sie in vier Gruppen, ohne die Reihenfolge zu stören:2 + 3 + 4 + 5 = 14; 6 + 7 = 13; 8; 9. Die längste Länge beträgt 14.Wenn es zulässig ist, die Reihenfolge zu stören, können die Teile der Skala leicht gruppiert werden:2 + 9; 3 + 8; 4 + 7; 6 + 5. Jene. Die Stablänge wird auf 11 reduziert.Literatur
1. Apokin I.A., Maistrov L.E. "Die Geschichte der Computertechnologie: Von den einfachsten Computergeräten bis zu komplexen Relaissystemen." (Moskau: Nauka-Verlag, 1990)2. www.mechrech.infoPS
Eine Frage für diejenigen, die Französisch sprechen: Wie zum Teufel ist es richtig, die Namen von Genaille und Lucas richtig zu übersetzen?UPD: Danke. Korrigiert im gesamten Artikel über Zhenai (Klasse) und Luke (Nichtklasse) Source: https://habr.com/ru/post/de380549/
All Articles