"Inspektionsparadoxon" ist überall

Viele Menschen kennen das sogenannte "Freundschaftsparadoxon" in sozialen Netzwerken, das erstmals in der wissenschaftlichen Arbeit von 1991 erwähnt wurde, als soziale Netzwerke nur offline waren. Dieses Paradoxon gilt für moderne soziale Netzwerke im Internet.

Wenn Sie einen Facebook-Benutzer nehmen und zufällig einen seiner Freunde auswählen, hat ein Freund mit einer Wahrscheinlichkeit von 80% mehr "Freunde". Menschen, die neu in der mathematischen Statistik sind, sind sehr verärgert darüber, dass fast alle Freunde in der Kommunikation „erfolgreicher“ sind als sie selbst. Es gibt jedoch keinen Grund für eine Depression: Dies sollte in Übereinstimmung mit der Wissenschaft und dem gesunden Menschenverstand der Fall sein.

Das Freundschaftsparadoxon ist eine der Formen des „Inspektionsparadoxons“, das überall zu finden ist und die Stadtbewohner oft in die Irre führt.

Das Wesen des Freundschaftsparadoxons besteht darin, dass Benutzer mit einer großen Anzahl von Freunden eher in die statistische Stichprobe fallen. Laut der Stanford Large Network Dataset Collection hat der durchschnittliche Facebook-Benutzer beispielsweise 42 Freunde in einer Stichprobe von 4.000 Personen, und jeder dieser Freunde hat durchschnittlich 91 Freunde.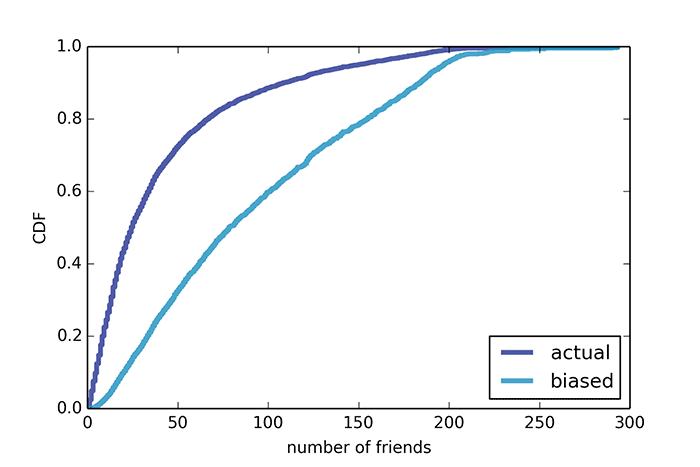



Gleiches gilt für andere Forschungsbereiche.

Zum Beispiel das Paradox der Klassengröße. Angenommen, wir befragen die Schüler, wie viele Personen in einer Gruppe mit ihnen lernen, und leiten dann aus ihren Antworten das arithmetische Mittel ab - und wir erhalten 56 Personen. Aber die Universitätsverwaltung sagt, dass die durchschnittliche Anzahl der Studenten in einer Gruppe 31 ist. Seltsamerweise lügt niemand und beide Werte sind fair. Gerade während der Umfrage werden Schüler aus großen Gruppen eher in die Stichprobe aufgenommen, da es tatsächlich mehr von ihnen gibt. Wenn wir zwei Gruppen mit 10 und 100 Personen haben, geben 100 von 110 Befragten die Größe ihrer Gruppe auf 100 Personen an, und nur 10 Personen geben die Größe der Gruppe 10 an. Die durchschnittliche Gruppengröße beträgt laut dieser Umfrage 92 Studenten.

Es scheint ein alltäglicher Fehler zu sein, aber es ist eine Quelle von Missverständnissen in vielen realen Situationen. Zum Beispiel bei der Analyse des Personenverkehrs im öffentlichen Verkehr. Ein Informatikprofessor, Allen Downey, liefert für einen Artikel im Journal der American Statistical Society ein Beispiel für die durchschnittliche Zeit zwischen Zügen der Roten Linie in Boston. Er zeichnete die Ankunftszeit von 70 Zügen zwischen 17:00 und 18:00 Uhr auf.



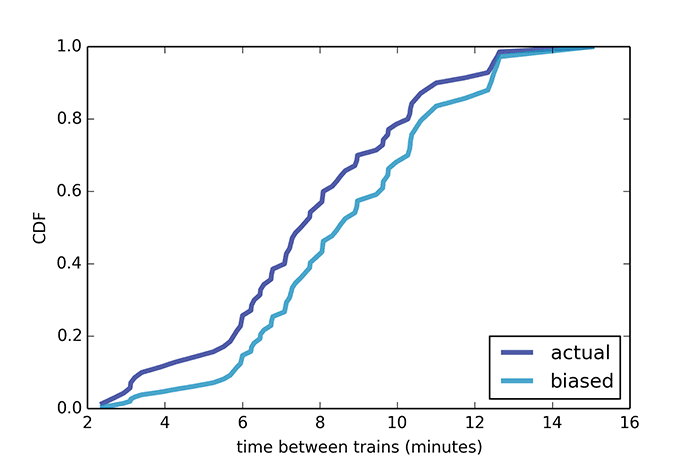Das Mindestintervall zwischen den Zügen betrug 3 Minuten, das Maximum 15 Minuten. Nach tatsächlichen Daten beträgt das durchschnittliche Intervall zwischen den Zügen 7,8 Minuten, dh die durchschnittliche Wartezeit für einen Zug sollte etwa 3,9 Minuten betragen. Eine Passagierumfrage zeigt jedoch, dass die durchschnittliche Wartezeit tatsächlich 4,4 Minuten betrug und das Intervall zwischen den Zügen 8,8 Minuten oder 15% mehr betrug.

Der Grund ist, dass mit einer größeren Verspätung im Zug mehr Fahrgäste darauf warten, während Züge, die mit einem kürzeren Intervall ankommen, weniger überfüllt sind. Dementsprechend beschweren sich die meisten Fahrgäste über das Gedränge im Auto und die lange Wartezeit auf den Zug, während nach Angaben des Unternehmens die durchschnittliche Zeit und Ladung der Autos normal ist.

Das gleiche Problem mit Flügen. Die meisten Passagiere sprechen von vollen Kabinenlounges, während sich Fluggesellschaften über Gewinneinbußen beschweren, weil so viele Flüge fast leer fliegen. Beides ist richtig.

Das „Inspektionsparadoxon“ wird beispielsweise bei Langstreckenrennen oder bei Autofahrten entlang der Autobahn beobachtet. In jedem dieser Fälle überholt der Teilnehmer der Bewegung „zu langsam“ und wird von „zu schnell“ überholt. Es entsteht ein subjektiver Eindruck, dass alle Teilnehmer der Bewegung in zu langsam oder zu schnell, aber nicht durchschnittlich unterteilt sind.

Das jüngste Beispiel für Allen Downey wurde geboren, nachdem er Oranges Hit of the Season gelesen hatte, eine Abhandlung von Piper Kerman, der 13 Monate im Bundesgefängnis verbracht hatte. In einem der Fragmente des Buches drückt sie ihre Überraschung über die lange Dauer der Strafen aus, die Gefangene verbüßen. Offensichtlich ist das Mädchen mit den Gesetzen der mathematischen Statistik nicht vertraut. Wenn Sie jedoch gemäß dem Inspektionsparadoxon zu einem zufälligen Zeitpunkt ins Gefängnis gehen und einen zufälligen Gefangenen auswählen, wird er mit hoher Wahrscheinlichkeit zu einer langen Haftstrafe verurteilt. Dies ist kein Beweis für das unmenschliche Gefängnissystem der Vereinigten Staaten, sondern eine einfache Schlussfolgerung aus dem Paradox der Inspektion.



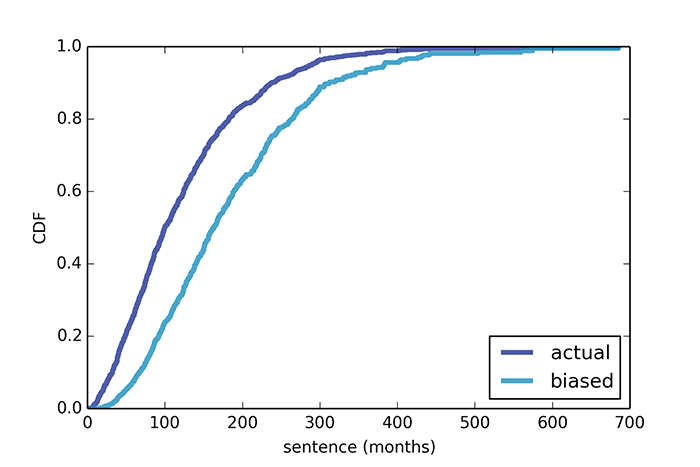Nach offiziellen Angaben der US-Strafkommission beträgt die durchschnittliche Haftstrafe 121 Monate und die „subjektive durchschnittliche Haftstrafe“ für die Befragung von Gefangenen 183 Monate.

Selbst wenn dreizehn Monate lang umliegende Gefangene befragt werden, unterscheidet sich das durchschnittliche Ergebnis, wie die Berechnung zeigt, nicht wesentlich von der ersten einmaligen Umfrage.



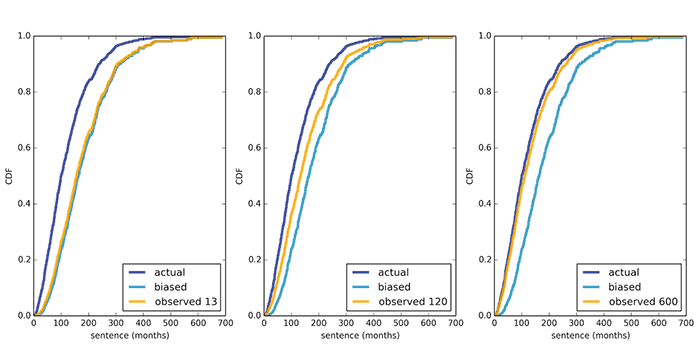Eine mehr oder weniger objektive Zahl kann durch Befragung für 600 Monate oder länger erhalten werden.

Source: https://habr.com/ru/post/de383787/