Einige Beschleunigungssensoren erfordern nach der Montage auf der Platine eine zusätzliche Nullkalibrierung. Als ich mehrere Quellen mit der Kalibrierung von Beschleunigungssensoren sah, bei denen die G-Komponente einfach durch Subtrahieren des Wertes = 9,8 m / s2 von der Z-Achse berücksichtigt wurde, kam die Idee auf, diese Notiz zu schreiben.
Publikationsstruktur
- Problem
- Erklärung des Problems und der Lösungsmethode
- Wie bekomme ich die Punkte?
- Wie berechnet man die Mitte des Balls?
- Wie kann die Suche nach der Mitte des Balls beschleunigt werden?
- Wie kann man sonst die Suche nach der Mitte des Balls beschleunigen?
- Über Messfehler
- Gesamt
Problem
Was ist das Problem? MEMS-Sensoren unterliegen nach dem Einbau in die Platine geringfügigen Verformungen, die Folgendes betreffen:- Nullposition;
- Skalierung von Messwerten;
- die Rechtwinkligkeit der Achsen zueinander.
Und wenn Skalierung und Rechtwinkligkeit nicht so merklich verletzt werden, verwickelt sich die Position Null spürbar. Wenn Sie beispielsweise den typischen Wert des Nullpunktversatzes für den Beschleunigungsmesser des MPU9250-Sensors in m / s 2 übersetzen , wird dieser im Bereich von 0,2 m / s 2 erhalten . Das heißt, der Sensor ist stationär, zeigt jedoch eine Beschleunigung an und nach 5 Sekunden erhalten wir eine Geschwindigkeit von 1 m / s. Einerseits werden alle Sensordaten immer durch eine Art Filter geleitet (z. B. einen solchen ). Warum sollte der Filter diese Vorspannung jedoch ständig ausgleichen? Immerhin zeigt der Sensor eine Bewegung an, wo sie nicht ist. Dies verringert die Genauigkeit des Ergebnisses. Alles in allem müssen Sie den Versatzwert einmal finden und diesen Wert dann während des Sensorbetriebs von seinen Messwerten abziehen.Die einfachste Lösung zum Ermitteln des Werts des Nullpunktversatzes, die sofort in den Sinn kommt, besteht darin, die Bedingungen zu erstellen, unter denen der Sensor genau Null anzeigen muss. Der auf dem Sensor aufgezeichnete Wert ist der Wert des Nullpunktversatzes! Damit? Aber auf den Beschleunigungsmesser wirkt ständig keine Schwerkraft. Um dies zu vermeiden, ist Schwerelosigkeit erforderlich (das Werfen funktioniert nicht). Das Erdmagnetfeld wirkt auf den Kompass und seine Rotation auf das Gyroskop. Wenn Sie also kein persönliches Raumschiff haben, müssen Sie sich etwas einfallen lassen.Die zweite Lösung, die sofort in den Sinn kommt, besteht darin, den Sensor (oder vielmehr seine Achse) in eine Position zu bringen, in der wir genau wissen, was der Sensor anzeigen soll. Der Unterschied zwischen dem, was der Sensor anzeigt und dem, was er anzeigen sollte - und es wird einen Nullpunktversatz geben! Damit? Zum Beispiel wissen wir, dass, wenn der Beschleunigungsmesser in einer Höhe mit dem Horizont platziert wird, der Gravitationsbeschleunigungsvektor theoretisch genau entlang der Z-Achse des Sensors gerichtet ist. Die Größe des Beschleunigungsvektors, den wir kennen.Es gibt jedoch ein Problem. Es besteht darin, dass wir die Achse des Sensors nicht genau auf eine Höhe mit dem Horizont einstellen können. Tatsache ist, dass die Oberfläche, auf die wir uns verlassen werden, nicht parallel zur Leiterplatte ist. Dies ist wiederum nicht parallel zu der Stelle, an der sich der Sensor befindet. Der Sensor selbst steht nicht genau an seiner Stelle und die Achsen im Sensor sind nicht parallel zum Sensorkörper. Der Fehler beim Einstellen der Achse relativ zum Horizont um 1 Grad ergibt eine Projektion, deren Größe mit dem Wert des Nullpunktversatzes selbst vergleichbar ist, den wir finden möchten. Im Fall eines Magnetometers wissen wir auch nicht, wohin der Magnetfeldvektor gerichtet ist. Theoretisch nach Norden. In der Praxis ist das Erdmagnetfeld selbst in Intensität und Richtung heterogen. Außerdem nehmen Metallobjekte in der Nähe ihre Anpassungen vor.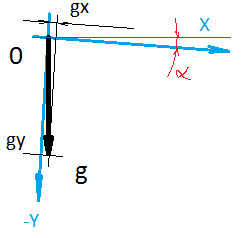
Erklärung des Problems und der Lösungsmethode
Die Aufgabe lautet wie folgt: Wir müssen den Nullpunktverschiebungsvektor anhand der Sensorwerte bestimmen, die immer den Verschiebungsvektor + den konstanten externen Einflussvektor (Gravitationsbeschleunigung, Erdrotation, Erdmagnetfeld) aufzeichnen, dessen Größe und Richtung wir nicht kennen (im Fall des Beschleunigungsmessers) Wir kennen den Wert, aber auch hier ist die Skala des Sensors möglicherweise nicht gleich 1).Der Weg zu lösen. In diesem Artikel wird vorgeschlagen, den Verschiebungsvektor wie folgt zu bestimmen. Wir nehmen und drehen den Sensor in jeder Hinsicht und registrieren die Sensorwerte. Nach N Messungen sind die vom Sensor entnommenen und im Diagramm befindlichen Werte eine Kugel, deren Radius die Größe des äußeren Aufpralls ist und deren Mittelpunkt der exakte gewünschte Nullpunktversatz ist.Wie bekomme ich die Punkte?
Um den Messvorgang selbst zu vereinfachen, können Sie ein einfaches Programm schreiben. Es sollte die Sensoren aufzeichnen, wenn das Gerät stationär ist. Wir müssen das Gerät nur in die gewünschte Position drehen. Um einen stationären Zustand zu bestimmen, ist auch ein nicht kalibrierter Beschleunigungsmesser geeignet - nehmen Sie einfach die Differenz zwischen dem aktuellen und dem vorherigen Wert. Und wenn es mehr Geräusche gibt, korrigieren wir die Bewegung. Mein Schwellenwert liegt im Bereich von 0,07 G. Wenn Sie mit Ihren Händen halten, wird sich mehr als dieser Wert herausstellen. Ich habe Klebeband verwendet, um die Position zu fixieren. Wenn es immer noch nicht funktioniert, überprüfen Sie, ob sich in der Nähe ein Kühlschrank, ein Ventilator oder ähnliches befindet.Wie kann es im Code sein
static TSumSensorsData g_sens_data[2];
static int32_t g_sens_data_sum_cnt[2];
static uint8_t g_sens_data_num;
IS_INTERRUPT void on_dma_raw_ready_calibrate_step1()
{
SensorRawBuffer *raw = sensor_get_raw_buffer();
g_sens_data[g_sens_data_num].acc_x += swap_i16(raw->accell_x_unswap);
g_sens_data[g_sens_data_num].acc_y += swap_i16(raw->accell_y_unswap);
g_sens_data[g_sens_data_num].acc_z += swap_i16(raw->accell_z_unswap);
g_sens_data[g_sens_data_num].gyro_x += swap_i16(raw->gyro_x_unswap);
g_sens_data[g_sens_data_num].gyro_y += swap_i16(raw->gyro_y_unswap);
g_sens_data[g_sens_data_num].gyro_z += swap_i16(raw->gyro_z_unswap);
g_sens_data[g_sens_data_num].mag_x += raw->mag_x_raw * g_mag_calibrate.kx;
g_sens_data[g_sens_data_num].mag_y += raw->mag_y_raw * g_mag_calibrate.ky;
g_sens_data[g_sens_data_num].mag_z += raw->mag_z_raw * g_mag_calibrate.kz;
g_sens_data_sum_cnt[g_sens_data_num]++;
}
void sensors_calibrate_program(FlashROM *flash_ptr)
{
double calibrate_result_error[3];
TVector16 calibrate_result[3];
int32_t radius[ACCEL_NO_MOTION_DETECT_COUNT];
uint8_t raw_is_deleted[ACCEL_NO_MOTION_DETECT_COUNT];
TVector16 raw[3][ACCEL_NO_MOTION_DETECT_COUNT];
. . .
g_sens_data_sum_cnt[0] = 0;
g_sens_data_num = 0;
int16_t prev_avg_x = 0;
int16_t prev_avg_y = 0;
int16_t prev_avg_z = 0;
int8_t low_motion_cnt = 0;
while(low_motion_cnt < ACCEL_NO_MOTION_DETECT_COUNT)
{
if (g_sens_data_sum_cnt[g_sens_data_num] >= ACCEL_NO_MOTION_DETECT_SAMPLES)
{
uint8_t new_data_num = (g_sens_data_num + 1) & 1;
g_sens_data[new_data_num].acc_x = 0;
g_sens_data[new_data_num].acc_y = 0;
g_sens_data[new_data_num].acc_z = 0;
g_sens_data[new_data_num].gyro_x = 0;
g_sens_data[new_data_num].gyro_y = 0;
g_sens_data[new_data_num].gyro_z = 0;
g_sens_data[new_data_num].mag_x = 0;
g_sens_data[new_data_num].mag_y = 0;
g_sens_data[new_data_num].mag_z = 0;
g_sens_data_sum_cnt[new_data_num] = 0;
uint8_t old_data_num = g_sens_data_num;
g_sens_data_num = new_data_num;
int16_t avg_x = g_sens_data[old_data_num].acc_x / g_sens_data_sum_cnt[old_data_num];
int16_t avg_y = g_sens_data[old_data_num].acc_y / g_sens_data_sum_cnt[old_data_num];
int16_t avg_z = g_sens_data[old_data_num].acc_z / g_sens_data_sum_cnt[old_data_num];
int16_t dx = avg_x - prev_avg_x;
int16_t dy = avg_y - prev_avg_y;
int16_t dz = avg_z - prev_avg_z;
prev_avg_x = avg_x;
prev_avg_y = avg_y;
prev_avg_z = avg_z;
if ((abs_i16(dx) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dy) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dz) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE))
{
raw[RAW_ACC][low_motion_cnt].x = avg_x;
raw[RAW_ACC][low_motion_cnt].y = avg_y;
raw[RAW_ACC][low_motion_cnt].z = avg_z;
raw[RAW_GYRO][low_motion_cnt].x = g_sens_data[old_data_num].gyro_x / g_sens_data_sum_cnt[old_data_num];
raw[RAW_GYRO][low_motion_cnt].y = g_sens_data[old_data_num].gyro_y / g_sens_data_sum_cnt[old_data_num];
raw[RAW_GYRO][low_motion_cnt].z = g_sens_data[old_data_num].gyro_z / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].x = g_sens_data[old_data_num].mag_x / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].y = g_sens_data[old_data_num].mag_y / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].z = g_sens_data[old_data_num].mag_z / g_sens_data_sum_cnt[old_data_num];
low_motion_cnt++;
beep();
delay_ms(2000);
}
}
}
. . .
}
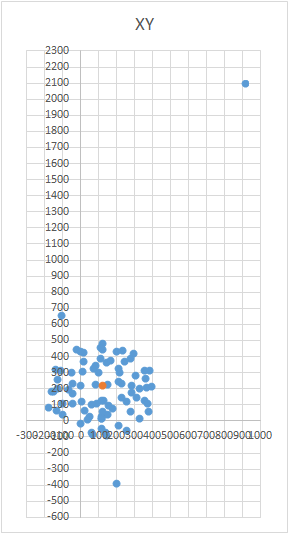
Um den Ball in die Grafik zu bringen, müssen Sie das Gerät mit dem Sensor nach einem bestimmten Schema drehen. Für diese Zwecke ist der Globus gut geeignet, da er einen Aufschlag hat. Sie könnten denken, dass Sie auf der ganzen Welt formen müssen. Aber das ist nicht so.Beispiel für ein falsches Ergebnis Der Sensor muss nicht auf der gesamten Erdoberfläche, sondern auf einem Meridian geformt werden. Nehmen wir an, wir nehmen sieben Punkte auf dem Meridian (der erste und der letzte am Nord- und Südpol). An jedem Punkt des Meridians befestigen wir Ihr Gerät am Globus und drehen das Gerät dennoch mit einem bestimmten Schritt um seine Achse, z. B. 30-35 Grad. Es stellt sich heraus, dass bei 12-maliger Drehung um die Achse an 7 Punkten insgesamt 84 Messungen erhalten werden.
Das Schöne an der Methode ist, dass alles „am Knie“ gemacht werden kann. Die Positioniergenauigkeit spielt keine besondere Rolle. Sie müssen sich nur gemäß dem Schema drehen, damit der Vektor des externen Einflusses auf das Diagramm eine Kugel zeichnet. Das richtige sieht ungefähr so aus - siehe Abbildung (die Mitte ist mit einer Markierung markiert).
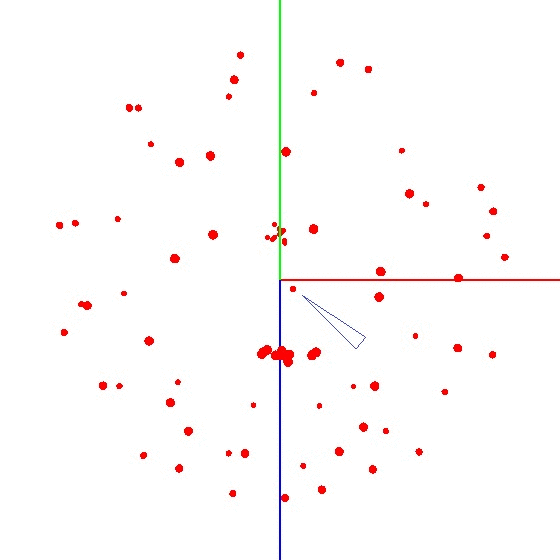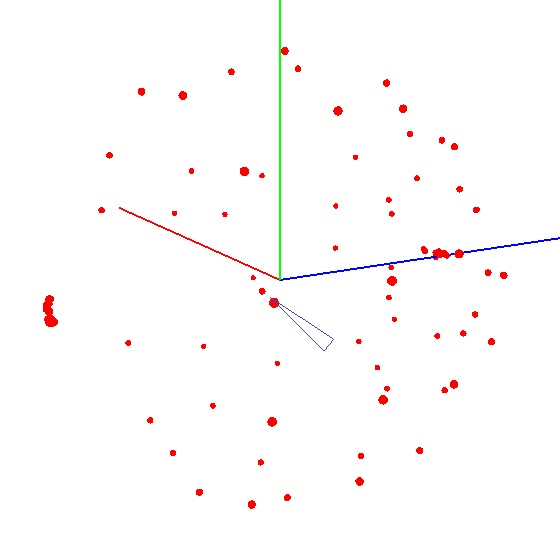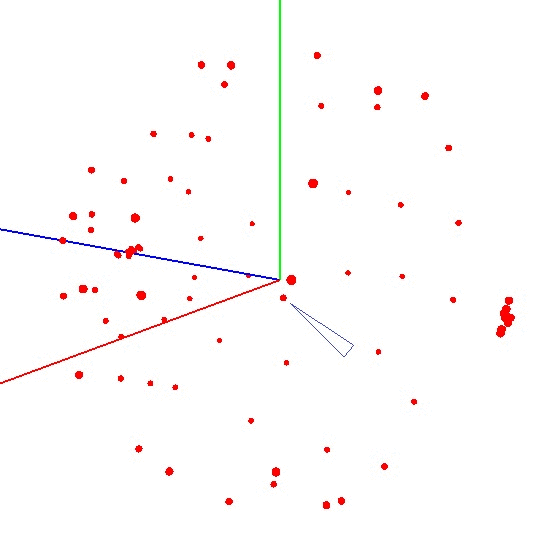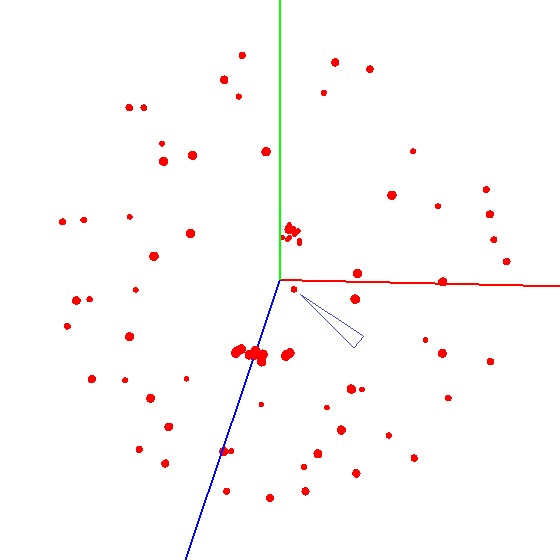
Wie berechnet man die Mitte des Balls?
Dies ist eine interessante Aufgabe und hat mehrere Lösungen. Es mag scheinen, dass es für die Suche nach dem Zentrum ausreicht, den arithmetischen Durchschnitt der Koordinaten der erhaltenen Punkte zu nehmen. Dies ist jedoch nicht der Fall - die Punkte können ungleichmäßig auf dem Ball liegen (siehe Abb.).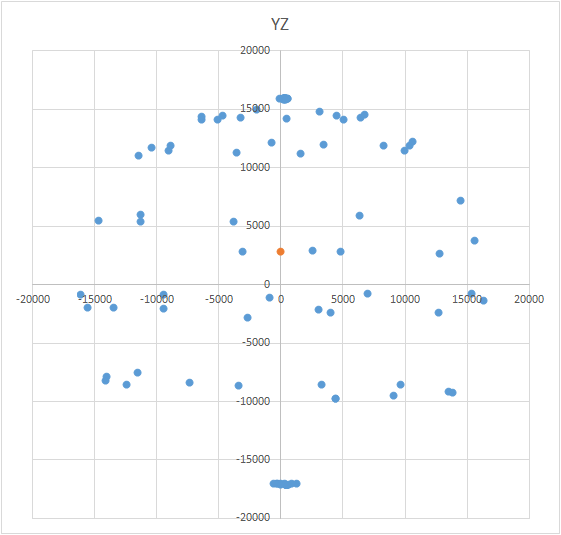
Die Gleichung des Balls sieht folgendermaßen aus: (X - A) 2 + (Y - B) 2 + (Z - C) 2 = R 2 , wobei X, Y, Z die Koordinaten des auf dem Ball liegenden Punktes sind. A, B, C sind die Koordinaten des Zentrums auf der x-, y- und z-Achse. R ist der Radius der Kugel. Sie können ein Gleichungssystem erstellen und versuchen, dieses System einfacher mit einer Methode zu lösen. Oder Sie können einfach pleite gehen, um das Zentrum zu finden (dies ist wie eine Methode aufeinanderfolgender Approximationen). Die Bedeutung der Methode ist einfach: der Fehlerwert (X - A) 2 + (Y - B) 2+ (Z - C) 2 - R 2 sollte gegen Null tendieren. Dies bedeutet, dass die Summe dieser Größen für alle Punkte der Kugel ebenfalls gegen Null tendieren sollte. Wenn wir dies wissen, können wir die Werte A, B und C wählen, für die der Fehler für alle Punkte minimal ist. Der Suchbereich ist durch die Größe des Balls (bedingter Würfel) begrenzt. Das heißt, wir müssen die Mitte des Balls nacheinander an allen Punkten des Würfels platzieren und den Fehler berechnen. Wo es nur minimale Fehler gibt, gibt es das Zentrum.
Als R müssen wir den theoretischen Wert des Vektors des äußeren Einflusses nehmen - für den Beschleunigungsmesser ist dies die Beschleunigung der Schwerkraft, für den Kompass - dies ist die durchschnittliche Größe des Erdmagnetfeldes, für das Gyroskop - die Rotationsgeschwindigkeit der Erde. Natürlich sollte die Formel Werte einer Dimension enthalten (herkömmliche Einheiten des Sensors oder m / s 2), Grad / s usw.). Es ist bequemer, in beliebige Einheiten des entsprechenden Sensors umzurechnen.Wie berechnet man einen bestimmten Wert in den Standardeinheiten des Sensors?= * / ( — )
: 16- ±2g ?:
9,8 /2 * 65536 / (2g + 2g) = 9,8 /2 * 65536 / (2 * 9,8 /2 + 2 * 9,8 /2) = 16384 . . .
Wenn Sie den Radius des Balls genau kennen, können Sie das Zentrum übrigens nur anhand seines „Keils“ berechnen. Das heißt, an Punkten, die sich nur auf einem Stück der Oberfläche der Kugel befinden. Dies ist jedoch nicht unser Fall.Wie kann die Suche nach der Mitte des Balls beschleunigt werden?
Es ist notwendig, das Zentrum nicht im gesamten Würfel (den Abmessungen der Kugel) zu suchen, sondern entlang der Linie, deren Anfang beliebig ist, wobei jeder nächste Punkt näher am realen Zentrum liegt und das Ende in der Mitte liegt. Angenommen, wir beginnen am Punkt (0; 0; 0) ... Wir bewegen uns immer mit einem konstanten Schritt. Wenn wir uns also einen Satz von 3x3x3-Würfeln vorstellen, bei denen jede Fläche der Schrittgröße entspricht, und uns auch vorstellen, dass die aktuelle Position der mittlere Würfel ist, haben wir 9 + 8 + 9 Optionen, wo der nächste Punkt platziert werden soll. Wir müssen nur an jedem Punkt sein, um zu berechnen, in welchem der benachbarten 26 Punkte der Fehler geringer sein wird. Wenn sich herausstellt, dass der Fehler am aktuellen Punkt geringer ist und nicht an einem der benachbarten, bedeutet dies, dass er sich in der Mitte befindet und die Suche beendet ist.
Wie kann es im Code seinPublic Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
Do While True
min_sigma = 0
For ai = -1 To 1
For bi = -1 To 1
For ci = -1 To 1
sigma = get_err(A + ai, B + bi, C + ci, 16384)
If sigma < min_sigma Or min_sigma = 0 Then
ai_min = ai
bi_min = bi
ci_min = ci
min_sigma = sigma
End If
Next
Next
Next
If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
Exit Do
End If
A = A + ai_min
B = B + bi_min
C = C + ci_min
Loop
. . .
Wie kann man sonst die Suche nach der Mitte des Balls beschleunigen?
Müssen mit variabler Tonhöhe suchen. Zuerst suchen wir das Zentrum in großen Schritten. Wir haben das Zentrum gefunden, wir reduzieren den Schritt und von dort aus beginnen wir weiter zu suchen. Und so weiter, bis Sie das Ergebnis der erforderlichen Genauigkeit erhalten.Wie kann es im Code seinPublic Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
step = 1000
Do While True
min_sigma = 0
For ai = -1 To 1
For bi = -1 To 1
For ci = -1 To 1
sigma = get_err(A + ai * step, B + bi * step, C + ci * step, 16384)
If sigma < min_sigma Or min_sigma = 0 Then
ai_min = ai
bi_min = bi
ci_min = ci
min_sigma = sigma
End If
Next
Next
Next
If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
step = step / 10
If step < 0.01 Then
Exit Do
End If
Else
A = A + ai_min * step
B = B + bi_min * step
C = C + ci_min * step
End If
Loop
. . .
Über Messfehler
Während der Messungen kann es Situationen geben, in denen das Messergebnis aus irgendeinem Grund viel weiter von der Oberfläche der Kugel entfernt ist. Oder es könnten viele Punkte sein. Oder im Allgemeinen ist das Ergebnis von Messungen möglicherweise kein Ball, sondern ein „Ei“ oder ein „Luftschiff“. In diesem Fall müssen Sie natürlich alle Messungen wiederholen und die möglichen Fehlerursachen identifizieren. Bei einem Magnetometer kann es sich beispielsweise um einen Bolzen oder einen Nagel in einem Tisch handeln, und Sie messen direkt darüber. Und je tiefer Sie den Sensor entlang des Meridians absenken, desto stärker wirkt sich das Metall auf das Ergebnis aus. Daher ist es notwendig, den Schwellenwert des zulässigen Fehlerwerts zu bestimmen. Um die Messungen aufgrund mehrerer eindeutig fehlerhafter Punkte nicht zu wiederholen, können Sie einen Filter anwenden. Das Prinzip des Filters ist sehr einfach: Nachdem Sie das Zentrum zum ersten Mal berechnet haben, sortieren Sie die Punkte nach der Fehlerstufe in jedem von ihnen.Einige der Punkte mit dem größten Fehler können einfach weggeworfen werden (z. B. 10%). Dann müssen Sie die Suche nach dem Zentrum wiederholen.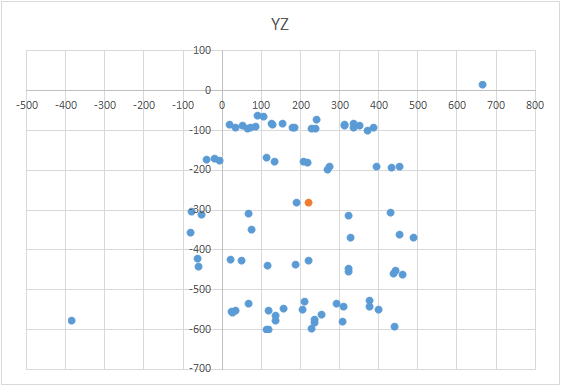
Gesamt
Die Methode hat eine ziemlich gute Genauigkeit. Die Methode ermöglicht es Ihnen, mit einfachen improvisierten Mitteln (Ball, Bank usw.) zu arbeiten. Es funktioniert schnell genug. Einfacher Code. Viele Sensoren haben spezielle Register, in die Sie den gefundenen Wert schreiben können, und der Sensor subtrahiert ihn im laufenden Betrieb. Solche Register haben normalerweise das Präfix "TRIM" wie beim MPU9260 oder "OFFSET" wie beim LSM303. Das bekannte LIS302DL verfügt jedoch nicht über solche Register.Vergessen Sie nicht, ein Pluszeichen anzubringen, wenn es Ihnen gefallen hat. Schreiben Sie in die Kommentare Ihre Methoden zur Kalibrierung von Sensoren.