🚙 🏐 👊🏿 Warum klingen manche Noten harmonisch zusammen? 💞 🏢 ㊙️

Haben Sie sich jemals gefragt, warum einige Noten besser zueinander passen als andere? Wie sind die Frequenzen ihrer Wellen verbunden? Warum klingen Noten einer Taste „gut“? Warum klingen die Noten im Akkord „gut“?

Die Antwort auf diese Frage bezieht sich auf das Konzept der „Konsonanz“ (dh „Konsonanz“) und der modernen Wissenschaft, der Psychoakustik. Konsonanz ist ein konsonanter, harmonischer Klang, und Dissonanz ist im Gegenteil abweichend oder unruhig.

Zunächst muss zwischen reinen Tönen, die gewöhnliche Sinuswellen sind, und echten Tönen, die von Musikinstrumenten reproduziert werden, unterschieden werden. Echte Töne bestehen in der Tat aus harmonischen Obertönen mit unterschiedlichen Amplituden. Somit ist jede Note, die auf einem Instrument gespielt wird, ein komplexer Klang, der aus einem Grundton und einer großen Anzahl von Obertönen besteht.

Ein Oberton ist eine Eigenfrequenz oberhalb der Grundfrequenz, und diejenigen Obertöne, deren Frequenzen sich auf die Grundfrequenz als ganze Zahlen beziehen, werden als Harmonische bezeichnet. In diesem Fall wird der Grundton als erste Harmonische betrachtet. Es stellt sich heraus, dass sich die Frequenzwerte jeder Harmonischen wie folgt auf den Grundton beziehen: f, 2f, 3f, 4f, ....

Harmonische Frequenzen beziehen sich auch als ganze Zahlen aufeinander und bilden die wichtigsten musikalischen Intervalle: 2: 1 ist eine Oktave, 3: 2 ist eine Quint, 4: 3 ist ein Quart usw. In verschiedenen Musikkulturen und in verschiedenen Perioden Im Laufe der Zeit war das Verhältnis zu den Konsonanz- und Dissonanzintervallen unterschiedlich. Zur Zeit von Pythagoras galten Oktave, Fünftel und Quart als Konsonantenintervalle, im 13. Jahrhundert kamen jedoch ein Drittel hinzu. All dies ist auf eine Veränderung des Musikgeschmacks zurückzuführen.

Ian Johnston schrieb das Buch Measured Tones, in dem die Theorie der Konsonanz (musikalische Konsonanz) beschrieben wurde. Darin vergleicht er die Dissonanz mit dem Würzen und stellt fest, dass wir sie alle unterschiedlich behandeln. Die Struktur unserer Ohren und unseres Gehirns ist unterschiedlich, daher sind auch unsere Konzepte von „gutem Klang“ unterschiedlich.

Lucas Biewald, Gründer von CrowdFlower, stimmt zu, dass „guter Sound“ ein sehr subjektives Konzept ist. Er sagt, welche Songs wir mögen, hängt von unserer Kultur, unserem Charakter und sogar unserer Stimmung ab.

Gehen wir weg von persönlichen Vorlieben und gehen wir etwas tiefer in die Physik laufender Prozesse ein. „Der Konsonant sind Noten mit der gleichen Tonhöhe. Mit anderen Worten, das Salz der kleinen Oktave des Klaviers stimmt mit der Note des Salzes (G) auf der Gitarre überein, sagt Bivald. „Hier ist ein Diagramm der Schallwelle, die von einer Gitarrensaite gespielt wird.“: Eine

Schallwelle ist eine Reihe von Luftschwingungen, die kleine Haarzellen im Innenohr einer Person dazu zwingen, mit unterschiedlichen Frequenzen zu schwingen. Der Klang, den wir hören, ist die Summe dieser Schwingungen. Um die in diesem Klang verborgenen Frequenzen hervorzuheben, wenden wir uns an die Mathematik und verwenden die Fourier-Transformation.

In der Grafik sehen wir, dass das Noten-Salz mehrere Frequenzen enthält. Die niedrigste Schwingungsfrequenz der Saite beträgt 196 Hz. Diese Frequenz wird als Grundfrequenz bezeichnet. Wir sehen jedoch, dass es Frequenzen gibt, die diese zwei- oder mehrmals überschreiten - dies sind Obertöne oder Harmonische.

Wenn Lucas Bivald eine Salznote sang, während er die Saite G auf der Gitarre schlug, erhielten wir die folgende Grafik:

Das Erscheinungsbild der Kurve ist unterschiedlich, aber wenn Sie die Frequenzdiagramme vergleichen, stimmen sie überein.

Rote Punkte zeigen die Oberwellenfrequenzen an. Zwischen ihnen genau 196 Hz, wie im vorherigen Fall. Bivald sagt: "Wenn ich eine Salznote singe und sie auf eine Gitarre nehme, wirken sich die Luftvibrationen, die von den Stimmbändern und der Instrumentensaite ausgehen, auf dieselben Haarzellen in meinem Ohr aus."

Schauen wir uns die Grafik an, die sich herausstellt, wenn Sie eine Salznote auf einer Gitarre spielen, aber eine Oktave höher. Es unterscheidet sich von den beiden vorherigen.

Wenn wir uns die Frequenzen der Harmonischen ansehen, werden wir feststellen, dass die Position einiger von ihnen übereinstimmt. Infolgedessen vibrieren in beiden Fällen fast die gleichen Ohrhaarzellen. Deshalb haben wir das Gefühl, dass dies zwei identische Noten sind, obwohl sie sich um eine Oktave unterscheiden.

„Zusätzlich zum Konzept einer Oktave haben wir noch das Konzept einer fünften. Die beiden Noten, die sich um ein Fünftel unterscheiden, sind am konsonantesten “, sagt Bivald. Das Verhältnis zwischen Noten zu und Salz beträgt ein Fünftel. Daher enthalten in der westlichen Musiktradition die meisten Akkorde, die aus einer Note aufgebaut sind, eine Note aus Salz. Aber warum passen sie so zusammen? Hier sind die Frequenzen der Note, die zuvor auf einer Bivald-Gitarre gespielt wurde.

Hier sind die Salzfrequenzen rot und die Noten von do gelb markiert. Es ist ersichtlich, dass sie sich nicht immer überlappen, aber da sich die Hauptfrequenz der Note auf die Grundfrequenz der Note als 3/2 bezieht, fallen jede dritte Harmonische des Salzes und jede zweite Harmonische von zusammen.

Es wird angenommen, dass die Noten, die am besten mit dem Do übereinstimmen, das Fa und das Salz sind, da sie sich in der Entfernung eines idealen Viertels bzw. eines idealen Quartetts befinden. Werfen wir einen Blick auf ihre Harmonischen.

Die Harmonischen von Salz und Fa überschneiden sich häufig zuvor. Die Harmonischen von Salz und Fa fallen jedoch seltener um eine Größenordnung zusammen. Wenn wir die Noten salt + do und fa + do hören, scheinen sie uns daher konsonant zu sein, und wenn wir das Fa + salt hören, bekommen wir ein Gefühl der Dissonanz. Aus diesem Grund werden diese drei Noten fast nie gleichzeitig aufgenommen. Schauen Sie sich nun eine detailliertere Grafik an:

Es ist zu sehen, dass es vor und mi viele übereinstimmende Harmonische gibt, daher bilden die Noten von do, salt und mi einen Akkord in C-Dur. Do und Dis (Es) haben die gleiche Anzahl von Harmonischen, daher bilden die Noten Es und Salz einen Moll-Akkord. Wenn die Harmonischen von Noten nicht miteinander korrelieren, hören wir bei ihrer gleichzeitigen [Noten-] Wiedergabe eine Dissonanz. Zum Beispiel vor und Fis - sie haben keine überlappenden Harmonischen. Sie können mehr darüber in einer anderen Antwort von Lucas Bivald lesen.

Es gibt andere psychoakustische Effekte, die unsere Wahrnehmung von Schall beeinflussen. Dissonanz entsteht in dem Moment, in dem wir zwei Töne mit fast identischen, aber immer noch unterschiedlichen Frequenzen hören.

Mit der Zeit nimmt die Phasenverschiebung zu:

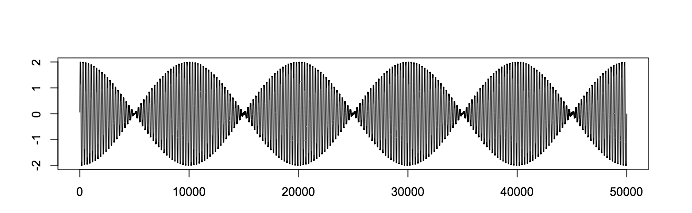
Wir hören die Summe der blauen und orangefarbenen Signale:

Wenn wir die Zeitachse verlängern, erhalten wir:

Wenn die Signale in Phase sind, verstärken sie sich gegenseitig und es treten verstärkende Interferenzen auf. Wenn die Verschiebung auftritt, tritt eine schwächere Interferenz auf und die Signale beginnen sich gegenseitig aufzuheben, bis sie streng gegenphasig sind.

Aus diesem Grund entsteht ein pulsierender Klang, den Sie wahrscheinlich gehört haben (spielen Sie auf einer verärgerten Gitarre oder einem Klavier). Für einen westlichen Zuhörer scheint er nicht übereinstimmend zu sein, aber diese Technik wird in der Musik einiger Kulturen verwendet.

PS Fühlen Sie sich frei, von schreibgeschützten Konten zu kommentieren, wir werden versuchen, die Moderation so schnell wie möglich durchzuführen, Freunde :)

Warum klingen manche Noten harmonisch zusammen?

More articles: