Geekly articles weekly

Messung der Harmonie - Schallspektrumanalysator bei STM32L4 Discovery

In einem früheren Beitrag haben wir einen billigen chinesischen LCD-Bildschirm an das STM32L4 Discovery Board angeschlossen . Jetzt werden wir versuchen, auf dieser Kombination etwas zu implementieren, das über das herkömmliche Blinken einer LED hinausgeht, nämlich einen Schallspektrumanalysator, der das Mikrofon auf der Platine verwendet. Gleichzeitig werde ich Ihnen erklären, wie Sie das FreeRTOS-Betriebssystem verwenden, warum es benötigt wird und warum eine Musikoktave 12 Noten enthält und mehr als 53 Noten besser als 12 sind.





Ton Digitalisierung


Wir möchten das Signal vom Mikrofon empfangen, sein Spektrum mithilfe der schnellen Fourier-Transformation (FPU, um uns zu helfen) berechnen und das Ergebnis in Form eines „Farbwasserfalls“ auf dem LCD anzeigen. Die Schallstärke wird farblich kodiert. Wir zeichnen eine Pixellinie vom Rand der Anzeige, wobei das am weitesten links stehende Pixel der minimalen Frequenz und das am weitesten rechts stehende dem Maximum entspricht, während das vorherige Bild um eine Linie verschoben wird, wodurch Platz für eine neue Linie frei wird. Unser Mikrocontroller ist zu kompliziert, um von vorne zu beginnen. Beginnen wir also mit einem Beispiel aus dem STM32Cube-Kit namens DFSDM_AudioRecord. Was ist DFSDM? Dies ist ein digitaler Filter für die Sigma-Delta-Modulation. Tatsache ist, dass im Gegensatz zu den guten alten analogen Mikrofonen das auf der Discovery-Karte kein Signal in Form einer dem Schalldruck proportionalen Spannung liefert.und als Folge von Nullen und Einsen mit einer Taktfrequenz von mehreren Megahertz. Wenn Sie diese Sequenz durch ein Tiefpassfilter leiten, erhalten Sie das gleiche analoge Signal. Bei früheren Modellen von Mikrocontrollern war es erforderlich, einen digitalen Filter herzustellen, um ein Audiosignal in digitaler Form zu empfangen. Jetzt hat der Mikrocontroller ein spezielles Modul dafür, und alles, was erforderlich ist, ist es, es zu Beginn des Programms zu konfigurieren. Dazu können Sie entweder die Dokumentation lesen oder ein vorgefertigtes Beispiel verwenden. Ich ging den zweiten Weg. Das folgende Bild zeigt die interne Struktur des Programms DFSDM_AudioRecord.Bei früheren Modellen von Mikrocontrollern war es erforderlich, einen digitalen Filter herzustellen, um ein Audiosignal in digitaler Form zu empfangen. Jetzt hat der Mikrocontroller ein spezielles Modul dafür, und alles, was erforderlich ist, ist es, es zu Beginn des Programms zu konfigurieren. Dazu können Sie entweder die Dokumentation lesen oder ein vorgefertigtes Beispiel verwenden. Ich ging den zweiten Weg. Das folgende Bild zeigt die interne Struktur des Programms DFSDM_AudioRecord.Bei früheren Modellen von Mikrocontrollern war es erforderlich, einen digitalen Filter herzustellen, um ein Audiosignal in digitaler Form zu empfangen. Jetzt hat der Mikrocontroller ein spezielles Modul dafür, und alles, was erforderlich ist, ist es, es zu Beginn des Programms zu konfigurieren. Dazu können Sie entweder die Dokumentation lesen oder ein vorgefertigtes Beispiel verwenden. Ich ging den zweiten Weg. Das folgende Bild zeigt die interne Struktur des Programms DFSDM_AudioRecord.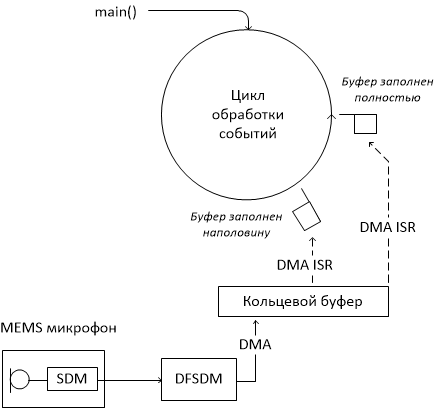



Der mit DMA digitalisierte Ton fällt in den Ringpuffer. DMA verursacht zweimal einen Interrupt: einmal - wenn der Puffer halb voll ist, das zweite Mal - wenn er voll ist. Die Interruptroutine setzt einfach das entsprechende Flag. Die Funktion main () führt nach der Initialisierung eine Endlosschleife aus, in der diese Flags überprüft werden und wenn das Flag gesetzt ist, die entsprechende Hälfte des Puffers kopiert wird. In einem Beispiel werden Daten in einen anderen Puffer kopiert, von wo aus sie erneut mit DMA an den Kopfhörerverstärker gesendet werden. Ich habe diese Funktionalität verlassen und die Berechnung des Spektrums des Audiosignals hinzugefügt.

Wenn es viele Aufgaben gibt


Die einfache Möglichkeit, unserem Code neue Funktionen hinzuzufügen, besteht darin, weitere Flags und Schreibfunktionen hinzuzufügen, die aufgerufen werden, wenn diese Flags gesetzt sind. Das Ergebnis ist normalerweise ein Durcheinander von Flags, Handlerfunktionen und dem globalen Kontext, der global sein muss, da die Lösung eines Problems in viele kleine Schritte unterteilt ist, die von einzelnen Funktionen implementiert werden - Ereignishandlern. Eine alternative Möglichkeit besteht darin, die Aufgabenverwaltung einem Betriebssystem wie FreeRTOS anzuvertrauen. Auf diese Weise können Sie die Logik erheblich vereinfachen, da jede Aufgabe innerhalb eines eigenen Zyklus von Verarbeitungsereignissen gelöst wird, die über die Funktionen des Betriebssystems miteinander interagieren. Zum Beispiel können wir eine Datenverarbeitungsaufgabe als separaten Zyklus hinzufügen.Dies wartet darauf, dass die Daten auf dem Synchronisationsprimitiv - Semaphor - bereit sind. Das Semaphor ist sehr einfach: Sie können es übergeben, wenn das Flag aktiviert ist und das Flag automatisch weggelassen wird. In unserem Fall setzt die Datenquelle ein Flag, wenn sie Daten für eine andere Aufgabe vorbereitet. Auf ähnliche Weise können Sie beliebige Ketten aus Datenquellen- und Datenkonsumententasks erstellen, ähnlich wie dies beispielsweise im Linux-Betriebssystem der Fall ist.im Linux-Betriebssystem.im Linux-Betriebssystem.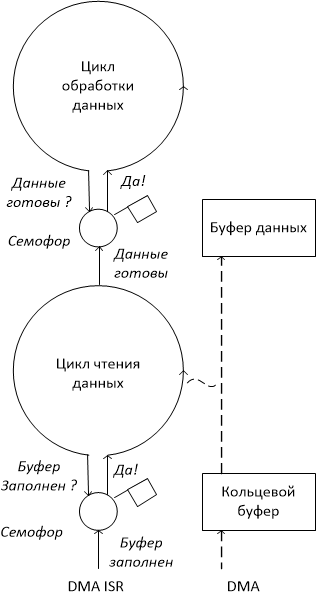



Natürlich ist die gleichzeitige Ausführung von Aufgaben eine Illusion, insbesondere wenn der Computerkern nur einer ist. In diesem Fall können wir sagen, dass wir einen einzelnen Thread der Programmausführung durch den Prozessor haben. Semaphoren spielen wie andere Synchronisationsprimitive die Rolle eines magischen Kaninchenlochs, in das der Ausführungsfluss bei einer anderen Aufgabe nicht auftaucht.

Das Verbinden von FreeRTOS mit Ihrem Projekt ist ganz einfach. Es ist nur erforderlich, die Endlosschleife, die normalerweise die main () - Funktion im Mikrocontroller beendet, durch einen Aufruf von osKernelStart () zu ersetzen. Danach erklärt Ihnen der Compiler genau, was ihm für die Kompilierung fehlt. Alle Aktionen, die Sie zuvor in der Schleife ausgeführt haben, müssen an eine separate Aufgabe übertragen und beim xTaskCreate-Aufruf registriert werden. Danach können Sie beliebig viele weitere Aufgaben hinzufügen. Es sollte beachtet werden, dass es zwischen den Aufrufen von xTaskCreate und osKernelStart besser ist, keinen Code zu platzieren, der mit Hardware funktioniert, da hier der System-Timer möglicherweise nicht richtig funktioniert. Der Aufruf des Timer-Handlers für das Betriebssystem osSystickHandler () muss zu SysTick_Handler () hinzugefügt werden, und die beiden Funktionen SVC_Handler und PendSV_Handler sollten aus ihrem Code entfernt werden.da sie im OS-Code implementiert sind. Bei der Registrierung von Aufgaben ist es wichtig, keinen Fehler mit der Größe des Stapels zu machen. Wenn es sich als zu klein herausstellt, kommt es an den unerwartetsten Stellen zu Abstürzen. Das erste, wenn der Stapel überläuft, ist die Struktur selbst, die die Aufgabe beschreibt. IAR kann eine Liste von Aufgaben anzeigen. Wenn Sie eine Aufgabe mit einem geänderten Namen sehen, müssen Sie den Stapel vergrößern.


Zur Berechnung des Spektrums verwenden wir die schnelle Fourier-Transformation. Die entsprechende Funktion befindet sich bereits in der Bibliothek. Sie erhält einen mit komplexen Daten gefüllten Puffer und bildet dort das Ergebnis. Dementsprechend benötigt sie am Eingang einen Puffer, in dem sich der digitalisierte Ton mit Nullen abwechselt (komplexer Teil 0). Am Ausgang erhalten wir komplexe Zahlen, für die wir sofort das Quadrat des Moduls berechnen, indem wir die Quadrate des Real- und Imaginärteils addieren. Wir machen das nur für die Hälfte des Puffers, weil das Spektrum symmetrisch ist. Wir würden die zweite Hälfte brauchen, wenn wir die inverse Transformation durchführen wollten, aber für eine einfache Anzeige des Spektrums wird sie nicht benötigt. Einige zusätzliche Anstrengungen sind erforderlich, um das Spektrum in verschiedenen Spektralbereichen berechnen zu können. Um das Spektrum für niedrige Frequenzen zu erhalten,Ich sammle Daten für mehrere Zyklen des Lesens des Puffers, wodurch die Abtastfrequenz des Tons, die anfänglich 44,1 kHz beträgt, effektiv reduziert wird. Das Ergebnis sind 6 Bereiche - 20 kHz, 10 kHz, 5 kHz, 2600 Hz, 1300 Hz, 650 Hz. Verwenden Sie zum Wechseln der Bereiche den Joystick und eine separate Aufgabe. Der Joystick übernimmt auch die Funktion zum Starten / Stoppen des „Wasserfalls“ sowie zum Einstellen der Empfindlichkeit. Es ist bequemer, das Spektrum in logarithmischen Einheiten (Dezibel) darzustellen, da sein Dynamikbereich normalerweise sehr groß ist und wir auf einer linearen Skala nur die stärksten Komponenten des Spektrums unterscheiden können. Der Logarithmus wird selbst auf der FPU als ziemlich lange Zeit angesehen, daher habe ich den realen Logarithmus durch eine stückweise lineare Näherung ersetzt, die leicht zu erhalten istDas Ergebnis sind 6 Bereiche - 20 kHz, 10 kHz, 5 kHz, 2600 Hz, 1300 Hz, 650 Hz. Verwenden Sie zum Wechseln der Bereiche den Joystick und eine separate Aufgabe. Der Joystick übernimmt auch die Funktion zum Starten / Stoppen des „Wasserfalls“ sowie zum Einstellen der Empfindlichkeit. Es ist bequemer, das Spektrum in logarithmischen Einheiten (Dezibel) darzustellen, da sein Dynamikbereich normalerweise sehr groß ist und wir auf einer linearen Skala nur die stärksten Komponenten des Spektrums unterscheiden können. Der Logarithmus wird selbst auf der FPU als ziemlich lange Zeit angesehen, daher habe ich den realen Logarithmus durch eine stückweise lineare Näherung ersetzt, die leicht zu erhalten istDas Ergebnis sind 6 Bereiche - 20 kHz, 10 kHz, 5 kHz, 2600 Hz, 1300 Hz, 650 Hz. Verwenden Sie zum Wechseln der Bereiche den Joystick und eine separate Aufgabe. Der Joystick übernimmt auch die Funktion zum Starten / Stoppen des „Wasserfalls“ sowie zum Einstellen der Empfindlichkeit. Es ist bequemer, das Spektrum in logarithmischen Einheiten (Dezibel) darzustellen, da sein Dynamikbereich normalerweise sehr groß ist und wir auf einer linearen Skala nur die stärksten Komponenten des Spektrums unterscheiden können. Der Logarithmus wird selbst auf der FPU als ziemlich lange Zeit angesehen, daher habe ich den realen Logarithmus durch eine stückweise lineare Näherung ersetzt, die leicht zu erhalten istEs ist bequemer, das Spektrum in logarithmischen Einheiten (Dezibel) darzustellen, da sein Dynamikbereich normalerweise sehr groß ist und wir auf einer linearen Skala nur die stärksten Komponenten des Spektrums unterscheiden können. Der Logarithmus wird selbst auf der FPU als ziemlich lange Zeit angesehen, daher habe ich den realen Logarithmus durch eine stückweise lineare Näherung ersetzt, die leicht zu erhalten istEs ist bequemer, das Spektrum in logarithmischen Einheiten (Dezibel) darzustellen, da sein Dynamikbereich normalerweise sehr groß ist und wir auf einer linearen Skala nur die stärksten Komponenten des Spektrums unterscheiden können. Der Logarithmus wird selbst auf der FPU als ziemlich lange Zeit angesehen, daher habe ich den realen Logarithmus durch eine stückweise lineare Näherung ersetzt, die leicht zu erhalten istFormat zur Darstellung einer Zahl in float32 . Das wichtigste Bit ist ein Zeichen. Die nächsten 8 Bits sind der binäre Exponent plus 127. Die verbleibenden Bits sind der Bruchteil der Mantisse, obwohl der ganzzahlige Teil 1 ist (der Einfachheit halber lassen wir die Nuancen denormalisierter Zahlen weg). Wenn Sie also den Exponenten aus float32 ausgewählt und die wichtigsten Punkte der Mantisse erfasst haben, können Sie eine gute Annäherung an den Logarithmus erhalten. Unter Verwendung der vorbereiteten Tabelle konvertieren wir die resultierende Zahl in einen RGB-Code zur Anzeige auf dem LCD. Es ergibt sich eine Farbskala von 90 oder 60 Dezibel. Der Lautstärkepegel, der Null dieser Skala entspricht, kann durch Drücken des Joysticks nach oben und unten eingestellt werden.

Wir zeigen ein Bild - über die Vorteile des Lesens von Datenblättern


Jetzt müssen wir nur noch das Bild anzeigen und unseren 'Wasserfall' wiederbeleben. Der einfachste Weg, dies zu tun, besteht darin, das Bild vom gesamten Bildschirm in einem Puffer zu speichern, dort zu aktualisieren und jedes Mal neu zu zeichnen, wenn neue Daten angezeigt werden. Diese Lösung ist nicht nur äußerst ineffizient, wir haben auch nicht genügend Speicher, um das gesamte Bild zu speichern. Es scheint, dass das LCD selbst genug Speicher dafür hat, und es sollte in der Lage sein, etwas Interessantes damit zu tun. In der Tat das Studium des DatenblattesErlaubt den bisher nicht verwendeten Bildlaufbefehl, mit dem Sie die Art und Weise, wie der Speicher des LCD-Controllers auf dem Bildschirm angezeigt wird, dynamisch ändern können. Stellen Sie sich vor, der Speicher ist ein Band, das in einem Ring eingeschlossen ist, den Sie unter dem Glas des Bildschirms sehen. Mit dem Befehl Startadresse für vertikales Scrollen (0x37) können Sie die Position auf dem Menüband festlegen, die dem oberen Bildschirmrand entspricht. Alles, was wir brauchen, um den 'Wasserfall' wiederzubeleben, ist, ein neues Spektrum an dieser Position aufzunehmen und durch das Speicherband zu scrollen. Der entsprechende Code wurde dem LCD-Treiber hinzugefügt, von dem seriösen Peter Drescher ausgeliehen und wie hier beschrieben angepasst. Der einzige Nachteil dieses Ansatzes: Das Scrollen funktioniert nur entlang der langen Seite des Bildschirms. Dementsprechend steht nur die kurze Seite für die Spektrumausgabe zur Verfügung.

12 ?


Kommen wir zu den praktischen Anwendungen unseres Geräts. Das erste, was im Spektrum leicht zu erkennen ist, sind Harmonische, dh Frequenzen, die ein Vielfaches der Grundfrequenz sind. Besonders viele von ihnen in der Stimme. Es gibt auch in den Klängen, die Musikinstrumente machen. Es ist leicht zu verstehen, warum sich die Noten benachbarter Oktaven in der Frequenz um das Zweifache unterscheiden: Dann stimmen die Noten einer höheren Oktave in der Frequenz mit der zweiten Harmonischen der Noten einer niedrigen Oktave überein. Sie sagen, dass sie gleichzeitig "im Einklang" klingen. Es ist etwas schwieriger zu verstehen, warum eine Oktave 12 Noten enthält - sieben Haupttöne (weiße Tasten auf der Klaviertastatur) plus fünf zusätzliche (schwarze Tasten). Zusätzliche Noten werden durch die Hauptnoten mit scharfen und flachen Zeichen angezeigt, obwohl es tatsächlich keinen Unterschied zwischen ihnen und den Hauptnoten gibt - alle 12 Noten bilden also einen geometrischen Verlaufdass das Verhältnis der Frequenzen zwischen benachbarten Noten gleich der Wurzel des 12. Grades von 2 ist. Die Bedeutung dieser Unterteilung der Oktave in Noten ist, dass es für jede Note andere Noten gibt, deren Frequenz sich um das Eineinhalbfache unterscheidet - diese Kombination wird als fünfte bezeichnet. Die Noten, aus denen die fünfte Note besteht, klingen im Einklang, da die zweite Harmonische einer Note in der Frequenz mit der dritten Harmonischen der anderen Note übereinstimmt. Das Foto unten zeigt die Spektren der Noten Do und Sol, die eine fünfte, passende Harmonische bilden, die gelb eingekreist sind.bilden eine fünfte, passende Harmonische sind gelb eingekreist.bilden eine fünfte, passende Harmonische sind gelb eingekreist.



Wie kommt es, dass Notizen 12? Da die Noten eine geometrische Folge bilden, gehen wir zu den Logarithmen über. ln (1,5) / ln (2) = 0,58496 ... Für den Bruch 7/12 = 0,583 wird ein enger Wert erhalten ... Das heißt, sieben Halbtöne (Intervalle zwischen benachbarten Noten) liegen sehr nahe am fünften, 1,498. Interessanterweise ergibt der Bruch 31/53 = 0,58491 .. eine viel größere Genauigkeit, so dass sich der fünfte von 1,5 nur in der fünften Dezimalstelle unterscheidet. Diese Tatsache blieb nicht unbemerkt, aber Musikinstrumente mit 53 Noten in einer Oktave wurden nicht verteilt. Sie sind schwer zu stimmen, sie sind schwer zu spielen und der Prozentsatz der Menschen, die den Unterschied zu herkömmlichen Werkzeugen spüren können, ist verschwindend gering.

Quellcode


Liegt hier . Für die Kompilierung wurde IAR Embedded Workbench für ARM 7.50.2 verwendet. Für die Kompilierung sind keine weiteren Bibliotheken erforderlich.

Source: https://habr.com/ru/post/de391311/

More articles:


All Articles