Willst du einen Anfänger Schachspieler rätseln?Bitten Sie ihn, mit einem Pferd und einem Elefanten Schachmatt zu setzen.Möchten Sie einen Programmieranfänger rätseln?Bitten Sie ihn, die Matte mit einem Pferd und einem Elefanten zu berechnen.
Schachprobleme regen die Fantasie des Programmierers an,weshalbich für die praktische Demonstration der Kombinatorik das schwierigste Schachproblem aus dem Zyklus „Schachmatt zum einsamen König“ ausgewählt habe.Zielsetzung
Ziel des Projekts ist es, eine Lösungsbasis zu schaffen, dh eine Liste der richtigen Bewegungen für alle möglichen Positionen des weißen Königs, des Elefanten, des Pferdes und des schwarzen Königs auf dem Schachbrett.In dieser Veröffentlichung werde ich Ihnen erzählen, wie ich dieses Problem gelöst habe, mit welchen Schwierigkeiten ich konfrontiert war und was am Ende passiert ist. Verwendete Technologien: C #, JavaScript, PHP, HTML, CSS.Als sehr mittelmäßiger Schachspieler habe ich nie gelernt, wie man schnell mit einem Pferd und einem Elefanten schachmatt setzt. Deshalb habe ich mich entschlossen, diesen Mangel mit meinen Programmierkenntnissen auszugleichen, alle möglichen Positionen zu sortieren und für jede den richtigen Zug zu finden.Bevor ich mindestens eine Codezeile schrieb, schlüpfte ich in einen „napoleonischen“ Plan, wie ich es mehrere Wochen lang machen würde. Ich wollte dieses Problem unbedingt von Anfang an lösen, indem ich alle matten Kombinationen sortierte. Und dann einen Schritt zurück, bis alle möglichen Optionen ausgeschöpft sind.Wie viele Möglichkeiten gibt es?
Auf einem Schachbrett befinden sich 64 Zellen. Wir haben vier Figuren.Die Anzahl der möglichen Kombinationen beträgt 64 * 64 * 64 * 64 = 16.777.216.Sie können nur einen weißbrüstigen Elefanten zurücklassen.Die Anzahl der Optionen wird halbiert: 64 * 32 * 64 * 64 = 8.388.608.So viele Positionen werden in unserer Datenbank mit Lösungen enthalten sein.Tatsächlich gibt es noch weniger Kombinationen: Zwei Teile können nicht auf einem Feld stehen, Könige können nicht auf benachbarten Feldern stehen, der schwarze König kann nicht unter dem Scheck stehen und so weiter. Mit Blick auf die Zukunft werde ich sagen, dass die Datenbank der Lösungen 5.609.790 Kombinationen umfasst. Das Array wird zu 67% gefüllt sein.Um den Algorithmus zu vereinfachen und den Zugriff auf die Datenbankdaten zu beschleunigen, habe ich beschlossen, keine Zeit damit zu verschwenden und ein vierdimensionales Array für alle Kombinationen zu erstellen.Die folgende Struktur ist zum Speichern jeder Kombination definiert: struct Combo
{
public Coord whiteKing;
public Coord whiteBishop;
public Coord whiteKnight;
public Coord blackKing;
}
Im Inneren wird eine andere Koordinatenstruktur verwendet, um die Koordinaten der Figur aufzuzeichnen, wobei der Index von 0 bis 63 berechnet werden kann, sowie mit einem überladenen Vergleichsoperator. public struct Coord
{
public byte x;
public byte y;
public int index
{
get { return x + y * 8; }
set { x = (byte) (value % 8);
y = (byte) (value / 8); }
}
public static bool operator == (Coord a, Coord b)
{
return a.x == b.x && a.y == b.y;
}
}
Diese Struktur erwies sich als sehr praktisch, um als Argument an verschiedene Hilfsfunktionen übergeben zu werden, zum Beispiel: bool isCheck (Combo combo);
bool isCheckmate (Combo combo);
bool isCheckByBishop (Combo combo);
Um das Ergebnis der Entscheidungsgrundlage dieser Struktur aufzuzeichnen, reicht es jedoch nicht aus, ...Weiße Box
Das Ziel unseres Programms wird es sein, eine „weiße Box“ zu erstellen, in der alle Positionen, in denen der „Zug weiß ist“ und für die bekannt ist, welcher Zug ausgeführt werden soll und durch wie viele Züge er garantiert schachmatt gesetzt wird, addiert werden.Ein wesentlicher Bestandteil der „White Box“ ist die folgende Struktur: struct WhitesMove
{
public Combo combo;
public byte moves;
public Coord moveFrom;
public Coord moveTo;
}
Der einfachste Weg, eine „weiße Box“ zu organisieren, besteht darin, eine vierdimensionale Matrix zu öffnen. Jede Dimension dieser Matrix entspricht der möglichen Position jeder Figur: WhitesMove [ , , , ] box = new WhitesMove [64, 32, 64, 64];
Die erste Dimension ist die Koordinate des weißen Königs.Die zweite Dimension ist die Koordinate des weißen Elefanten / 2. Diedritte Dimension ist die Koordinate des weißen Pferdes.Die vierte Dimension ist die Koordinate des schwarzen Königs.Die Hauptsache ist, ihre Reihenfolge nicht zu verwechseln :) Das Array wird zu 33% entladen sein, aber für die Verarbeitung sehr praktisch. In diesem Array werden 8.388.608 Einträge gespeichert, um Kombinationen zu lösen.Übrigens, bevor ich anfing, alle Suchalgorithmen zu schreiben, habe ich ein leeres Projekt erstellt und diese vierdimensionale Matrix initialisiert, um sicherzustellen, dass genügend Speicher vorhanden ist und es nicht erforderlich ist, etwas Zusätzliches zu erfinden. Anscheinend wirkte sich die Erfahrung mit der Teilnahme an Informatik-Olympiaden des letzten Jahrtausends, bei denen die Größe der Struktur 64 Kilobyte nicht überschreiten konnte, auf Turbo Pascal 7.0 aus.Idee des Algorithmus
Beschreiben Sie kurz die Hauptidee zur Lösung dieses Problems. Es basiert auf einem Breitensuchalgorithmus, der etwas geändert werden musste, da zwei Personen Schach spielen und nacheinander Züge ausgeführt werden. Daher benötigen wir anstelle einer Zeile zwei - "schwarz" und "weiß". Queue<BlacksMove> blackQueue = new Queue<BlacksMove>();
Queue<WhitesMove> whiteQueue = new Queue<WhitesMove>();
Mit der Struktur von WhitesMove haben wir uns bereits getroffen. Die Struktur von BlacksMove ist etwas einfacher, da der letzte Zug von Black nicht darin gespeichert werden muss.struct BlacksMove
{
public Combo combo;
public byte moves;
}
Zuerst platzieren wir in der „schwarzen Linie“ alle matten Positionen, an denen die Bewegung schwarz ist. Dann machen wir von jeder solchen Position aus einen umgekehrten Zug für Weiß und bilden eine „weiße Linie“ - eine Liste von Positionen, an denen sich Weiß bewegt.Diese Schritte müssen wiederholt werden, bis alle möglichen Kombinationen erschöpft sind.Der Hauptalgorithmus in Form von Pseudocode: " ", " ", " "
" "
{
" "
" "
" "
" "
" "
" "
" "
" "
" "
} " "
" "
Matte Position
Das Erstellen der Basis für die richtigen Züge beginnt mit der Suche nach allen Mattkombinationen. Die Verwendung von Enumeratoren ermöglichte es, diesen Prozess recht effektiv zu beschreiben. foreach (Combo combo in AllCheckmates())
{
BlacksMove checkmate = new BlacksMove { combo = combo, moves = 0 };
blackQueue.Enqueue(checkmate);
}
Insgesamt 232 matte Positionen gefunden. Ich möchte Sie daran erinnern, dass wir uns nur auf einen Weißfeldelefanten beschränkt haben.Einige von ihnen sind ziemlich exotisch, nicht existent und „kooperativ“. In diesem Moment kletterte der schwarze König selbst unter die Matte.
Schachspieler sind sich bewusst, dass eine Matte mit einem Pferd und einem Elefanten auf einem weißen Feld in einer weißen Ecke platziert werden muss. In der schwarzen Ecke ist Schachmatt nur möglich, wenn Schwarz mitspielt. Ich habe am Anfang des Artikels speziell ein Foto mit einem solchen Pseudo-Automaten gepostet, um die Aufmerksamkeit echter Schachspieler zu erregen :)Matte in einem Zug
Der nächste Schritt ist das Umkehren von Weiß. Das heißt, für jede gefundene matte Position müssen alle möglichen weißen Bewegungen zurückgehen .Wie mache ich einen Rückwärtsgang? Da in unseren Positionen keine Erfassung vorgesehen ist, ist der Algorithmus recht einfach - machen Sie eine Bewegung von Weiß, wonach der schwarze König nicht mehr überprüft wird.Alle auf diese Weise gefundenen Positionen können bereits in das „weiße Kästchen“ eingefügt werden. Dies zeigt an, dass sich eine Bewegung vor der Matte befindet und welche Art von Bewegung dies tun soll. Unterwegs setzen wir die Kombinationen in die „schwarze Linie“.So sieht dieser Teil des Algorithmus aus:
while (blackQueue.Count > 0)
{
BlacksMove black = blackQueue.Dequeue();
foreach (WhitesMove white in AllWhiteBackMoves(black))
if (!isCheck(white.combo))
if (!whiteBox.Exists(white.combo))
{
whiteBox.Put (white);
whiteQueue.Enqueue(white);
}
}
Übrigens über den Ertragyield- , , :
IEnumerable<WhitesMove> AllWhiteBackMoves(BlacksMove black)
{
foreach (WhitesMove white in AllWhiteKingMoves(black))
yield return white;
foreach (WhitesMove white in AllWhiteBishopMoves(black))
yield return white;
foreach (WhitesMove white in AllWhiteKnightMoves(black))
yield return white;
}
Insgesamt wurden 920 solcher Positionen gefunden, hier sind die interessantesten:Pferdebewegung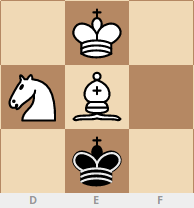
: Elefantenbewegung
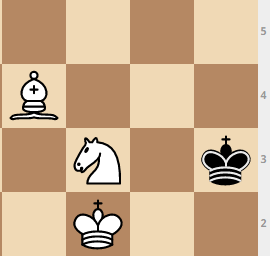
: Königsbewegung: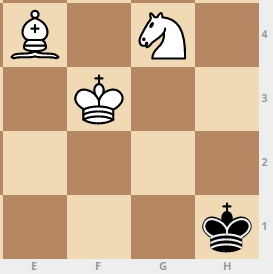
Matte in anderthalb Zügen
Der nächste Schritt ist das Umkehren von Schwarz. Mit diesem Algorithmus habe ich die längste Zeit verbracht, viele Fehler wurden gemacht, bevor alles richtig funktionierte.Auf den ersten Blick ist alles ähnlich wie in der vorherigen Version: Für jede Position von der „weißen Linie“ müssen alle möglichen Bewegungen des schwarzen Königs aussortiert werden. Und fügen Sie alle gefundenen Kombinationen zur „schwarzen Linie“ hinzu - schließlich handelt es sich um einen Schachmatt in anderthalb Zügen, von dem aus Sie dann wieder einen umgekehrten Zug für Weiß ausführen können - es gibt einen Schachmatt in zwei Zügen - und fahren Sie fort, bis alle Optionen überprüft wurden.Das war der Fehler. Mit jedem möglichen Zug bekommt Schwarz in anderthalb Zügen einen „kooperativen“ Schachmatt, aber in Wirklichkeit wird der König nicht unbedingt unter den Schachmatt gehen. Dmitry Grin hat mich auf diesen Fehler hingewiesen, der an allen meinen Webinaren zur Erstellung dieses Programms teilgenommen hat, für die ich ihm separat danke.Der richtige Algorithmus lautet wie folgt: Für jede Position N nach der Rückwärtsbewegung des schwarzen Königs müssen Sie alle möglichen direkten Bewegungen durchlaufen, um sicherzustellen, dass alle zu vertrauten Positionen aus der „weißen Box“ führen, dh zur Matte. Und erst nach dieser Position kann N zur „schwarzen Linie“ hinzugefügt werden. Und wenn der schwarze König von Position N „abrutschen“ kann, überspringen wir diese Option. Sie wird sich bei nachfolgenden Iterationen treffen, wenn es bekanntere Positionen geben wird.So sieht dieser Teil des Algorithmus aus:
while (whiteQueue.Count > 0)
{
WhitesMove white = whiteQueue.Dequeue();
Combo whiteFigures = white.combo;
foreach (BlacksMove black in AllBlackBackMoves(white))
{
bool solved = true;
foreach (Coord blackKing in AllKingMoves(black.combo.blackKing))
{
whiteFigures.blackKing = blackKing;
if (isCheck(whiteFigures))
continue;
if (box.Exists(whiteFigures))
continue;
solved = false;
break;
}
if (solved)
blackQueue.Enqueue(black);
}
}
Insgesamt wurden 156 Kombinationen von „Matteinhalb Zügen“ gefunden.Auf halbem Weg iterativ
Die beschriebenen Algorithmen zum Erstellen eines Halbpasses müssen geloopt werden. Aus der „schwarzen Linie“ bilden wir die „weiße Linie“ und dann umgekehrt - aus der „weißen“ Linie bilden wir die „schwarze Linie“. Und so weiter, bis alle neuen Positionen erschöpft sind. Das „weiße Kästchen“ wird in der Phase der Bildung der „weißen Linie“ ausgefüllt, da es die Positionen platziert, an denen sich Weiß bewegt.Der vorgefertigte Algorithmus zum Auflisten aller Optionen funktionierte irgendwo in 12 Minuten und blieb bei Schritt 33 stehen. So viele maximale Bewegungen sind erforderlich, um den schwarzen König aus jeder Position mit einem Pferd und einem Elefanten zu paaren.Übrigens gab es nicht so viele solcher „schwierigsten“ Positionen, nur 156, hier ist eine davon:
Mata wird nicht sein!
Es gibt viele Positionen, in denen der schwarze König auch nach dem Zug von Weiß einen Ritter oder Bischof essen und ein Unentschieden erzielen kann. Es gibt auch Pattoptionen. Hier sind einige der interessantesten Artikel.
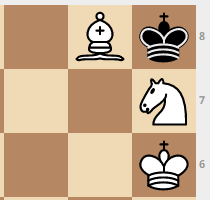
So speichern Sie eine Lösungsdatenbank
Wie speichere ich die gefundene Lösungsbasis?Der einfachste und falscheste Weg ist die Verwendung der Serialisierung. Das serialisierte vierdimensionale Array der Struktur benötigte 1,7 Gigabyte (!) Speicherplatz. Der Serialisierungsprozess dauerte ungefähr sechs Minuten, die Deserialisierung dauerte ungefähr das gleiche.Diese Option ist natürlich nicht geeignet. Darüber hinaus ist es in der Praxis nicht erforderlich, das gesamte vierdimensionale Array zu verwenden. Für eine bestimmte Werbebuchung wird nur ein Eintrag benötigt.Eureka! Um Platz zu sparen, können Sie die Speicherkoordinaten der Figuren für jede Kombination nicht mehr speichern. Wenn wir ein vierdimensionales Array haben, wird die Position jeder Figur auf der Tafel eindeutig durch ihren Index im Array bestimmt.Es wurde beschlossen, die gesamte Datenbank der Lösungen in einer Datei zu speichern - als linearer Scan eines vierdimensionalen Arrays. Für jede mögliche Position wird die Adresse berechnet, an der die richtige Antwort aufgezeichnet wird.Wie kann man die Antwort, die wir brauchen, so kompakt wie möglich aufzeichnen? Die Position der Figuren muss nicht gespeichert werden, daher bleiben nur drei Zahlen übrig - wie viele Züge auf die Matte, was und wohin. Auf diese Weise wird der richtige Schritt für Weiß eindeutig festgelegt.6 Bit Wie viele Züge auf die Matte gehen, ist eine ganze Zahl von 0 bis 33,2Bit. Welche Figur geht - drei mögliche Optionen, ein König, ein Elefant oder ein Pferd.6 Bit Wohin das Stück geht - der Feldindex auf der Tafel liegt zwischen 0 und 63.Für jeden Entscheidungsdatensatz reichen also zwei Bytes aus:1 Byte - wie viele Bewegungen auf die Matte oder 0, wenn die Position unbekannt ist.2 Bytes - FFNNNNNNFF - Nummer der zu gehenden Figur (1 - König, 2 - Elefant, 3 - Pferd)NNNNNN - Zellkoordinate - wohin (von 0 bis 63).Die Lösungsdatenbankdatei benötigt also 64 * 32 * 64 * 64 Wörter = genau 16 Megabyte. Die Position der Figuren wird durch die Koordinaten jedes Wortes im ersten Byte festgelegt - die Anzahl der Bewegungen auf der Matte (oder 0, wenn es keine Lösung gibt), die zweite Bewegung speichert die richtige Bewegung.Es wäre möglich, die Dateigröße um die Hälfte zu reduzieren, wenn Sie die Anzahl der Züge nicht auf der Matte gespeichert hätten, aber es wäre nicht interessant, so zu spielen.Koordinaten des schwarzquadratischen weißen Elefanten
Es ist Zeit, für die Optimierung zu bezahlen. Für Kombinationen mit einem „Schwarz-Weiß“ -Elefanten muss ein Algorithmus zur Neuberechnung der Koordinaten implementiert werden.Dies wurde wie folgt durchgeführt. Wenn die Koordinate des Elefanten auf ein schwarzes Feld fällt, müssen die Koordinaten aller Figuren auf dem Brett "umgedreht" werden. In diesem Fall bleibt die Y-Koordinate unverändert und X ändert sich zu 7-X. Eine visuelle Demonstration eines Koordinatenwechsels, siehe Abbildung.
Wenn der Elefant auf einem weißen Käfig steht, müssen Sie zuerst die Koordinaten aller Figuren "umdrehen". Suchen Sie dann nach einer Position in der Datenbank der Lösungen. Und noch einmal "drehen" Sie die Koordinate der korrekten Bewegung, die von dort gelesen wird.Visualisierung der Lösungsbasis
Damit ist das Problem gelöst!Die Datenbank der Lösungen wurde erstellt.Aber wie kann man das demonstrieren?Der naheliegendste Weg ist die Verwendung von Webtechnologien, sodass Sie nur einen Link zu einem funktionierenden Beispiel geben können. Nach meiner "Programmierformel " wurde bereits der Fotokurs " Nano-Schach " erstellt , bei dem unter Verwendung der Technologien HTML, CSS, JavaScript und PHP ein interaktives Schachbrett zum Spielen ohne Regeln für zwei Personen erstellt wurde. Dieses Skript wurde als Grundlage genommen.Ich ließ nur vier Teile übrig, entfernte die Möglichkeit der Erfassung, fügte PHP-Funktionen hinzu, um die richtigen Bewegungen von der Lösungsbasis zu lesen, und „hauchte Leben“ durch JavaScript.Auf der Seite www.videosharp.info/chess können Sie mit der Datenbank der Lösungen experimentieren.
Für jede Position werden Bewegungen sowohl für Weiß als auch für Schwarz berechnet.Für Weiß - der beste Zug, der zum Schachmatt führt.Für Schwarz - wie viele Züge auf die Matte für einen möglichen Zug.Sie können jede Bewegung der Figuren mit der Maus ausführen, nicht unbedingt nach den Regeln.Das Skript berechnet die Option für jede Position oder schreibt, dass es keine Optionen gibt.Es ist interessant zu spielen, die vorgeschlagenen Züge auszuführen oder die Stücke nach eigenem Ermessen zu bewegen.Fazit
Eine großartige, interessante Arbeit wurde geleistet, um das Schachproblem zu lösen.Wenn Sie dies auf diese Weise wiederholen möchten, können Sie Videos zum Erstellen dieses Programms von Grund auf bis zum Ergebnis mit detaillierten Erklärungen und unabhängigen Aufgaben ansehen .Viel Erfolg!