🅰️ 👩🏿‍🏭 🎉 Wir kommen in Form: von der hyperbolischen Geometrie zu kubischen Komplexen und umgekehrt 🙄 ☠️ 🌶️

Der Beweis markiert das Ende einer Ära in der Erforschung dreidimensionaler Formen.

Vor dreißig Jahren sprach der Mathematiker William Thurston über seine Vision: alle möglichen endlichen dreidimensionalen Formen zu systematisieren.

Thurston, Inhaber des Fields-Preises, der den größten Teil seiner Karriere an den Universitäten von Princeton und Cornell verbracht hatte, hatte die übernatürliche Fähigkeit, das Unvorstellbare darzustellen: nicht nur Formen, die im üblichen dreidimensionalen Raum leben, sondern auch eine viel größere Menge von Formen mit solch komplexen Eigenschaften, dass sie nur passen Raum mit vielen Dimensionen. Wo andere Mathematiker die Anfänge von Formen sahen, sah Thurston Strukturen: Symmetrien, Oberflächen, die Beziehung zwischen verschiedenen Figuren.

William Thurston 1991 in Berkeley.

„Nach vielen Jahren des Studiums haben viele Menschen den Eindruck, dass Mathematik ein strenges und formales Fach ist, das sich mit komplexen und undurchsichtigen Regeln befasst“, schrieb er 2009. "Gute Mathematik ist das genaue Gegenteil davon." Mathematik ist die Kunst des menschlichen Verstehens ... Mathematik singt, wenn wir es mit unserem ganzen Gehirn fühlen. “

Thurstons Vision basierte auf einer Verbindung zweier scheinbar unterschiedlicher Ansätze zur Untersuchung dreidimensionaler Figuren: Geometrie, ein bekanntes Königreich von Winkeln, Längen, Regionen und Volumina und eine Topologie, die die Eigenschaften von Formen untersucht, die unabhängig von genauen geometrischen Messungen sind - Eigenschaften, die es nicht sind Ändern, wenn die Form gedehnt oder verdreht ist, wie ein " Griff ".

Für einen Topologen entspricht die Oberfläche der Pfanne der Oberfläche eines Tisches, Bleistifts oder Balls. Die Oberfläche des Bechers entspricht einem Donut oder Torus. Aus der Sicht eines Topologen führt die Vielfalt der zweidimensionalen Formen - Oberflächen - zu einer einfachen Liste von Kategorien: sphärisch, toroidal und toroidal mit einer großen Anzahl von Löchern. (Die meisten von uns präsentieren Kugeln und Tori als dreidimensional, aber da Mathematiker sie als hohle Oberflächen betrachten, betrachten sie diese Oberflächen als zweidimensionale Objekte, gemessen an der Oberfläche, nicht am Volumen).

Thurstons Schlüsselidee war es, 3-Mannigfaltigkeiten zu verstehenmöglich durch die Vereinigung von Geometrie und Topologie. Ebenso wie die topologische Kategorie der 2-Mannigfaltigkeiten, die die Oberfläche einer Pfanne und eines Bleistifts enthält, auch eine ideale Kugel enthält, schlug Thurston vor, dass viele Kategorien von 3-Mannigfaltigkeiten eine Instanz enthalten, eine 3-Mannigfaltigkeit, deren Geometrie so homogen und perfekt und so schön ist dass, wie Walter Neumann von der Columbia University es ausdrückte, sie „wie eine Glocke läutet“. Darüber hinaus schlug Thurston vor, Formen, die keine solche Instanz haben, in Stücke zu schneiden, in denen sie bereits vorhanden sein werden.

In einer Arbeit von 1982 stellte Thurston seine „Geometrisierungshypothese“ unter 23 Fragen zu 3-Mannigfaltigkeiten vor, die Mathematikern die Richtung des Wissens über dreidimensionale Formen boten. (Es gab 24 Fragen auf der Liste, aber eine davon, die noch ungelöst ist, ähnelt eher einer faszinierenden Gasse als der Hauptstraße).

"Thurston hatte ein großes Talent, die richtigen Fragen zu stellen", sagt Vladimir Markovich, ein Mathematiker von Caltech. "Jeder kann Fragen stellen, aber es kommt selten vor, dass eine Frage zu Einsichten und Schönheit führt, so wie Thurstons Fragen erfolgreich waren."

Die Fragen inspirierten eine neue Generation von Mathematikern, von denen Dutzende beschlossen, ihre Arbeit unter der Leitung von Thurston durchzuführen. Seine mathematischen „Kinder“ drücken seinen Stil aus, wie Richard Brown schrieb.von der Universität. John Hopkins. "Sie betrachten Mathematik wie Kinder auf einer Messe: mit Freude und Überraschung, fasziniert von jeder neuen Entdeckung, und sie sind einfach froh, ein Teil von allem zu sein."

Dutzende von Jahren nach dem Erscheinen von Thurstons Werk folgten Mathematiker seiner „Karte“ der Forschung, und ihre Motivation wurde weniger durch die möglichen Anwendungen ihrer Entdeckungen als vielmehr durch den guten Platz, den 3-Mannigfaltigkeiten beim Studium von Formen einnahmen, gestärkt. Zweidimensionale Formen sind weit verbreitet, sie lassen sich leicht darstellen und in Kategorien einteilen. Vier-, fünf- und mehrdimensionale Formen sind praktisch unmöglich zu trainieren: Die Vielfalt der Möglichkeiten ist so groß, dass sich Mathematiker darauf beschränkten, nur ihre speziellen Unterklassen zu kennen. Und bei dreidimensionalen Strukturformen sind sie einerseits mysteriös und schwierig, andererseits sind sie grundsätzlich erkennbar.

Thurstons Arbeit ist 30 Jahre vergangen, und alle bis auf vier Probleme wurden bereits gelöst, einschließlich der Geometrisierungshypothese, die der russische Mathematiker Grigory Perelman im Jahr 2002 bewiesen hat und die ein Meilenstein in der modernen Mathematik war. Aber die vier verbleibenden Aufgaben widersetzten sich hartnäckig.

"Die Tatsache, dass wir sie so lange nicht lösen konnten, bedeutet, dass dort etwas sehr Tiefes verborgen ist", sagte Yair Minsky von der Yale University.

Schließlich erregte Ian Aigol von der University of California in Berkeley im März 2012 die Mathematik-Community, indem er den Beweis der Wise-Hypothese ankündigte , die Thurstons letzte vier Fragen auf einen Schlag abdeckte .

Mathematiker nennen dieses Ergebnis das Ende einer Ära.

"Die Vision von 3-Mannigfaltigkeiten, die Thurston damals in seiner Arbeit beschrieben hat, mag fantastisch ausgesehen haben, aber jetzt ist sie vollständig verwirklicht", sagt Danny Calegari von Caltech. "Seine Ideen wurden überraschend bewiesen - und jedes Detail war richtig."

"Es schien mir, dass es ein spezielles Wissen und spezielle Denkmethoden gab, die nur mir eigen waren", schrieb Thurston, der wenige Monate vor seinem Tod im August 2012 im Alter von 65 Jahren den mathematischen Preis von Steele erhalten hatte . "Und ich bin sehr froh, dass ich ein solches Niveau erreicht habe, wenn dies nicht so ist - viele Menschen teilten meine Denkweise und viele bewiesen die Theoreme, die ich erfolglos übernommen habe."

Aigols Leistung zeigt die Existenz eines einfachen Schemas zur Konstruktion aller kompakten hyperbolischen 3-Mannigfaltigkeiten - der einzigen Art dreidimensionaler Formen, die noch nicht vollständig erklärt wurde.

"Wir verstehen jetzt genau, wie alle 3-Mannigfaltigkeiten aussehen", sagte Henry Wilton vom London University College. "Dies ist der Höhepunkt einer riesigen mathematischen Erfolgsgeschichte."

Oberflächenstudie

Thurstons Programm versuchte mit 3-Mannigfaltigkeiten zu tun, was Mathematiker vor hundert Jahren mit zweidimensionalen Mannigfaltigkeiten erfolgreich gemacht haben. Um uns zu dehnen, bevor wir dreidimensionale Mannigfaltigkeiten verstehen, werfen wir einen Blick auf das Innere der Klassifizierung von „kompakt orientierbaren“ Oberflächen (endliche Oberflächen ohne Einstiche und Schnitte mit konstanter Ausrichtung).

Um sich dem Klassifizierungsproblem zu nähern, haben Mathematiker gezeigt, dass es für jede Oberfläche möglich ist, ihre sequentielle Vereinfachung durchzuführen, indem sie entlang der Kurven geschnitten wird, bis sie sich zu einem flachen Polygon öffnet.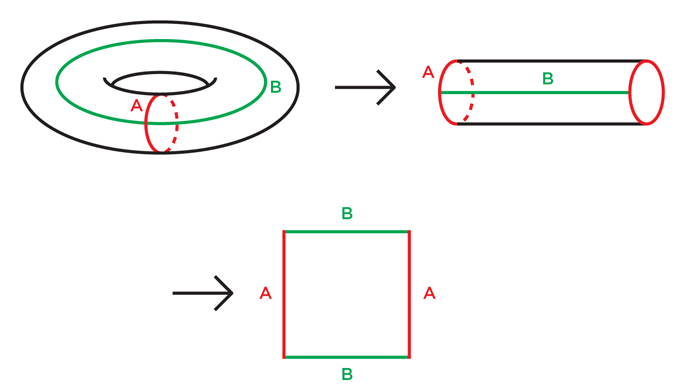

Abb. 1

Es ist leicht, dies für einen Torus zu zeigen: Zuerst schneiden wir es entlang der Schleife A, wie in Abb. 1, erhalten wir einen Zylinder. Dann schneiden wir entlang der Schleife B und richten den Zylinder zu einem Quadrat aus. Abb. 2 ist etwas schwieriger herauszufinden, aber selbst dort verwandelt das Schneiden entlang vier Kurven einen doppelten Torus (einen Torus mit zwei Löchern) in ein Achteck. Auf die gleiche Weise können wir für jeden Torus mit n Löchern 2n Kerben in die Schleifen machen und ihn zu einem 4n-Gon erweitern.

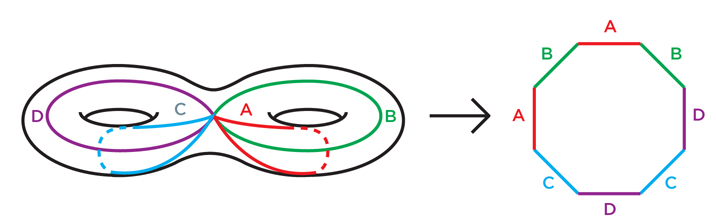Abb.2

Sie können versuchen, eine beliebige unbestimmte Oberfläche zu vereinfachen (und zu identifizieren), indem Sie sie auf ähnliche Weise schneiden. Wenn dies keine Kugel ist, haben Topologen gezeigt, dass sie interne Schleifen (Schleifen, die sich nicht schneiden) enthalten sollte, die nicht in einen Punkt gezogen werden können - wie A und B auf dem Torus. Durch Schneiden einer Oberfläche entlang einer dieser Schleifen werden einige interessante topologische Eigenschaften der Oberfläche entfernt. Mathematiker haben gezeigt, dass es notwendig ist, die Oberfläche endlich zu schneiden, um sie auf ein flaches Polygon zu reduzieren.

Nachdem wir die Oberfläche auf das Niveau des Polygons vereinfacht haben, ist es leicht zu erkennen, dass wir einen Torus oder einen doppelten Torus oder einen dreifachen Torus usw. herstellen müssen, wenn wir seine Kanten kleben, um die ursprüngliche Oberfläche wiederherzustellen. Schließlich verwandelt das erste Kleben das Polygon in die Oberfläche der Tunnelansicht, und jedes nachfolgende fügt entweder einen neuen Tunnel hinzu oder näht einfach offene Teile. Wenn wir den Prozess beenden, erhalten wir einen Torus mit einigen Löchern.

Dieser Ansatz demonstriert nicht nur die topologische Äquivalenz einer Oberfläche zu einer Kugel oder einem Torus, sondern bietet auch die Möglichkeit, eine Oberfläche mit einer einfachen und einheitlichen geometrischen Struktur auszustatten.

Die Kugel hat offensichtlich bereits eine einheitliche geometrische Struktur: Ihre Geometrie sieht von jedem Ort in der Kugel gleich aus. Im Gegensatz dazu ist die Donutoberfläche überhaupt nicht gleichmäßig: Der Bereich der Außenkante des Donuts ist ähnlich wie eine Kugel gebogen, und der Bereich am Innenring ist wie ein Sattel gebogen.

Und egal wie Sie den Torus im Raum platzieren - egal wie Sie ihn dehnen und drehen - Sie können ihn nicht so gestalten, dass die Geometrie an jedem Ort gleich ist. Einige Teile werden sich wie eine Kugel runden, andere wie ein Sattel, andere können flach sein.

Es ist jedoch möglich, den Torus mit einer abstrakten geometrischen Struktur auszustatten, die an jedem Punkt identisch ist. Erklären Sie einfach, dass auf jedem der kleinen Abschnitte des Torus die Abstände und Winkel bestimmt werden, indem Sie das Quadrat messen, aus dem, wie wir gesehen haben, der Torus hergestellt werden kann. Ein physikalischer Torus im gewöhnlichen Raum, dessen Längen und Winkel dieser abstrakten Regel entsprechen, kann nicht konstruiert werden, aber diese Definition von Längen und Winkeln ist intern konsistent. Da das Quadrat die übliche flache (euklidische) Geometrie hat, sagen wir, dass der Torus mit einer euklidischen Struktur ausgestattet werden kann. Ein Torus mit einer solchen Geometrie ähnelt einem Videospiel, bei dem ein Charakter von der linken Seite des Bildschirms verschwindet und auf der rechten Seite wieder erscheint und von der oberen Seite verschwindet.

Wenn wir versuchen, diese Operation mit einem doppelten Torus durchzuführen, werden wir auf ein Hindernis stoßen. Denken Sie daran, dass wir einen doppelten Torus herstellen können, indem wir die Kanten eines Achtecks kleben. Wenn wir erklären, dass die Geometrie des doppelten Torus die Geometrie des Achtecks kopieren soll, werden wir auf das Problem seiner Winkel stoßen. Nach dem Einkleben des Achtecks in einen doppelten Torus werden die Eckpunkte zu einem Punkt des doppelten Torus zusammengeklebt. An diesem Punkt gibt es acht Winkel, von denen jeder 135 Grad hinzufügt, was zusammen 1080 Grad statt 360 Grad ergibt.

Wenn wir versuchen, dem doppelten Torus die geometrische Struktur des Achtecks zu geben, stellt sich heraus, dass unser doppelter Torus überall die übliche euklidische Geometrie aufweist, mit Ausnahme eines Punktes, an dem seine Oberfläche wie ein spitzer Hut hervorsteht (Eckpunkte sind kein Problem, wenn wir ein Quadrat in einen Torus kleben: Wir kleben vier rechte Winkel und erhalten die perfekten 360 Grad).

Um eine glatte geometrische Struktur am Eckpunkt des doppelten Torus zu erhalten, muss jeder der acht Winkel nur 45 statt 135 Grad beitragen. Es ist interessant, dass ein solches Achteck existiert, aber nicht in der üblichen euklidischen Ebene lebt, sondern auf einer anderen Struktur, die als hyperbolische Scheibe bezeichnet wird: dem dritten Eine Art von Geometrie, die einheitlich und intern konsistent ist, wie sphärisch oder euklidisch. Da es jedoch schwieriger vorstellbar ist, wurde es erst zu Beginn des 19. Jahrhunderts von Mathematikern entdeckt.

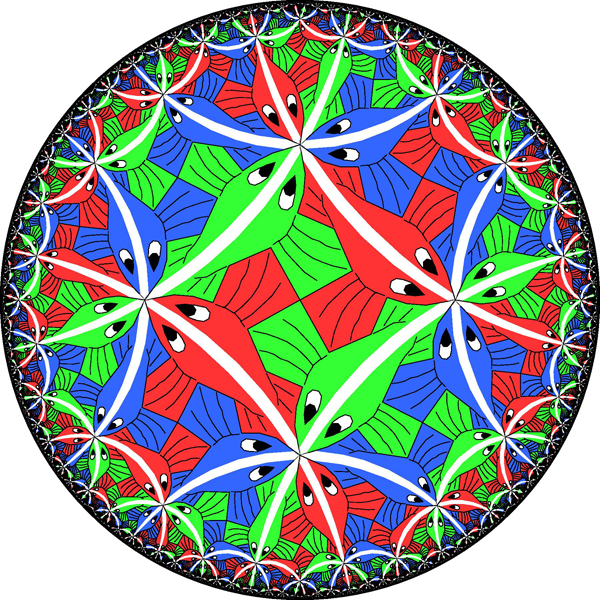Abb.3

Grob gesagt wird eine hyperbolische Geometrie (oder Lobachevsky-Geometrie) erhalten, wenn wir erklären, dass alle Fische in 3 die gleiche Größe haben. Man kann sich vorstellen, dass Fig. 3 tatsächlich ein Scheibenbild ist, das durch eine verzerrende Linse erhalten wird, wodurch der Fisch näher am Rand kleiner als der Fisch in der Mitte wird. Auf einer echten hyperbolischen Scheibe vor der Linse sind alle Fische gleich groß.

Im normalen Raum ist es unmöglich, eine normale und glatte hyperbolische Scheibe herzustellen, so dass alle Fische wirklich gleich sind. Aus abstrakter Sicht ergibt die Fischgrößenregel jedoch eine Geometrie, die intern konsistent ist und an jedem Punkt gleich aussieht - nicht für einen Beobachter mit einer verzerrenden Linse, sondern aus der Sicht eines Bewohners einer hyperbolischen Scheibe.

In der hyperbolischen Geometrie ist der kürzeste oder „geodätische“ Weg zwischen zwei Punkten der Weg durch die kleinstmögliche Anzahl von Fischen. Ein solcher Pfad ist immer ein Halbkreis senkrecht zur Plattengrenze. Beispiele sind Halbkreise, die entlang der Stacheln von Fischen verlaufen. Aus unserer verzerrten Sicht sind diese Pfade gekrümmt, aber für einen Bewohner der Platte sind dies gerade Linien. Wie Thurston sagte, müssen Sie das Lenkrad nicht drehen, um daran entlang zu fahren. Im Gegensatz zur euklidischen Ebene, auf der parallele Linien immer im gleichen Abstand bleiben, können auf einer hyperbolischen Scheibe zwei disjunkte Linien sehr schnell voneinander abweichen.

Unter dem Gesichtspunkt der hyperbolischen Geometrie sind die Figuren in Fig. 4 gewöhnliche Achtecke mit geraden Seiten. In einem dieser Achtecke sind alle 45-Grad-Winkel genau das, was wir für einen doppelten Torus benötigen. Wenn wir die Seiten dieses Achtecks richtig kleben, erhalten wir einen doppelten Torus mit einer idealen und gleichmäßigen hyperbolischen Struktur.

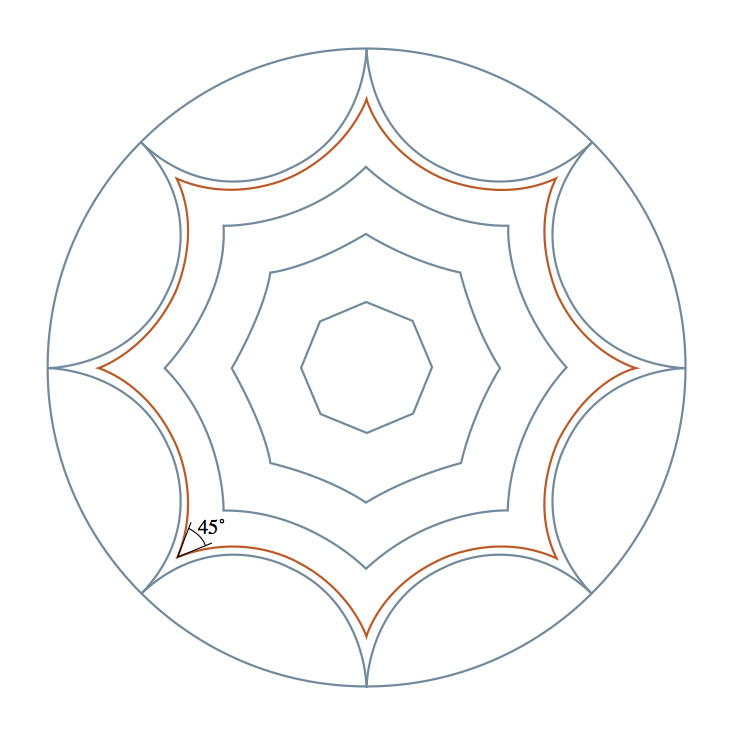Abb. 4

Auf die gleiche Weise können wir den dreifachen Torus mit einer hyperbolischen Struktur ausstatten. Der dreifache Torus kann aus einem 12-Gon geklebt werden. Wenn wir also einen hyperbolischen 12-Gon mit Innenwinkeln von 30 Grad herstellen, kann seine hyperbolische Geometrie reibungslos auf den dreifachen Torus übertragen werden. Wenn wir das Thema fortsetzen, können wir einen Torus mit 4 Löchern mit der fünften und so weiter hyperbolischen Geometrie bereitstellen. Unsere Klassifizierung von kompakten Oberflächen lautet wie folgt: eine Oberfläche mit sphärischer Geometrie (Kugel), eine mit euklidischem (Torus) und unendlich viele Oberflächen mit hyperbolischer Geometrie (alle Tori mit mehr als einem Loch).

In den letzten hundert Jahren hat diese Klassifizierung Mathematikern eine sehr fruchtbare Methode gegeben, um topologische Fragen zu Oberflächen in den geometrischen Bereich zu übertragen und umgekehrt. Die Klassifizierung von Oberflächen ist die Hauptidee bei der Untersuchung zweidimensionaler Formen, eine Entdeckung, die von allen anderen Studien als Ausgangspunkt verwendet wird.

Nächste Messung

3-Mannigfaltigkeiten sind viel vielfältiger als 2-Mannigfaltigkeiten, und Probleme mit ihnen sind komplizierter. Selbst eine einfach aussehende Frage wie die berühmte Poincaré-Vermutung, in der gefragt wird, ob die dreidimensionale Version der Kugel die einzige kompakte dreidimensionale Form ist, auf der jede Schleife zu einem einzigen Punkt gezogen werden kann, ohne das Loch zu erfassen, blieb nach ihrer Formulierung durch Henri Poincare im Jahr 1904 fast hundert Jahre lang ungelöst Jahr.

Thurston schlug jedoch mutig vor, dass es möglich ist, eine Klassifizierung dreidimensionaler Formen zu erstellen, die der bestehenden Klassifizierung zweidimensionaler Formen ähnelt.

Zweidimensionale euklidische, sphärische und hyperbolische Geometrien haben Paare in drei Dimensionen. In drei Dimensionen ist die Liste der „schönen“ Geometrien jedoch nicht auf diese beschränkt. Es gibt hybride Geometrien, die in bestimmten Richtungen hyperbolisch oder kugelförmig und in anderen euklidisch sind. Im Allgemeinen gibt es acht verschiedene Arten von Geometrien in drei Dimensionen, die in dem Sinne einheitlich sind, dass die Geometrie an jedem Punkt im Raum gleich aussieht.

Thurston schlug vor, dass 3-Mannigfaltigkeiten wie bei Oberflächen mit natürlichen geometrischen Strukturen verglichen werden können. Insbesondere schlug er vor, dass, wenn Sie einen kompakten 3-Verteiler auf besondere Weise in Stücke schneiden, jedes Stück einer von acht Geometrien zugeordnet werden kann.

„Ziel war es, Topologie und Geometrie in drei Dimensionen vollständig zu vereinheitlichen“, sagt Minsky.

Der natürliche Ansatz für diese „Geometrisierungshypothese“ bestand darin, etwas Ähnliches wie bei Oberflächen zu versuchen, die wir entlang von Kurven geschnitten haben, bis sie alle interessanten topologischen Eigenschaften enthüllten und bis sie sich zu einem flachen Polygon vereinfachten. Bei 3-Verteilern werden sie auf ähnliche Weise entlang von Oberflächen geschnitten, bis sie sich hoffentlich zu einem Polyeder vereinfachen, dessen gegenüberliegende Seiten zusammengeklebt werden können, um die ursprüngliche Form zu erhalten. Und wenn wir dieses Polyeder mit der richtigen Geometrie bauen können, können wir diese Geometrie in ihre ursprüngliche Form umwandeln, wie dies bei Oberflächen der Fall war.

Denken Sie daran, dass bei Flächen jede Kurve zwei Anforderungen erfüllen musste: Die Kurve schneidet sich nicht mit sich selbst (Mathematiker sagen, dass sie „eingebettet“ sein sollte), und sie sollte, wie wir es nennen, topologisch interessant sein, dh einige umgeben das topologische Detail der Oberfläche, so dass es nicht bis zu einem Punkt gezogen werden kann (diese Anforderung stellt sicher, dass das Schneiden entlang dieser Kurve die Oberflächentopologie vereinfacht).

Der Mathematiker Wolfgang Haken hat 1962 bewiesen, dass eine 3-Mannigfaltigkeit zu einem Polygon vereinfacht werden kann, wenn die 3-Mannigfaltigkeit eine Oberfläche enthält, deren Schnitt zwei Bedingungen erfüllt: Sie muss eingebettet und „inkompressibel“ sein, dh topologisch interessant Eine Kurve auf der Oberfläche wird auch im allgemeineren Kontext der umgebenden 3-Mannigfaltigkeit topologisch interessant sein.

Beispielsweise ist ein Torus im gewöhnlichen dreidimensionalen Raum nicht inkompressibel, da die durch die Öffnung des Torus verlaufende Schleife aus Sicht der Oberfläche des Torus topologisch interessant ist, im dreidimensionalen Raum jedoch auf einen Punkt komprimiert werden kann. Umgekehrt ist ein Torus innerhalb eines 3-Verteilers inkompressibel, was durch Verdicken der Oberfläche des Torus erreicht werden kann, so dass er nicht mehr unendlich dünn ist. Um inkompressibel zu sein, muss jedes topologische Merkmal der Oberfläche eine interne Topologie des 3-Verteilers widerspiegeln. Jetzt wird ein 3-Verteiler mit eingebauter inkompressibler Oberfläche als Haken-Verteiler bezeichnet.

Wenn unser 3-Verteiler eine eingebaute inkompressible Oberfläche hat, werden beim Schneiden einige interessante Topologien sichtbar und wir erhalten einen vereinfachten Verteiler. Darüber hinaus hat Haken gezeigt, dass, wenn ein Verteiler eine solche Oberfläche enthält, der neue Verteiler, der durch Schneiden erhalten wird, auch ein Haken-Verteiler ist: Er hat auch eine eingebaute inkompressible Schneidfläche. Und nach einer endlichen Anzahl solcher Schritte, wie Haken gezeigt hat, werden alle interessanten topologischen Merkmale des ursprünglichen Verteilers abgeschnitten und ein einfaches Polyeder bleibt erhalten.

In den späten 1970er Jahren zeigte Thurston, dass es möglich ist, das resultierende Polyeder mit einer von acht achtdimensionalen Geometrien so auszustatten, dass es reibungslos auf das neu geklebte Polygon übergeht und an den Ecken und Kanten des Polyeders perfekt übereinstimmt. Mit anderen Worten, Thurston hat seine Geometrisierungshypothese für jene Mannigfaltigkeiten bewiesen, deren Standardzerlegung zu Stücken führt, die Haken-Mannigfaltigkeiten sind.

Leider gibt es für einen beliebigen kompakten 3-Verteiler keine Garantie dafür, dass er eine solche Oberfläche hat. In den späten 1970er und frühen 1980er Jahren überzeugte Thurston die Community, dass 3-Mannigfaltigkeiten mit einer eingebetteten inkompressiblen Oberfläche (Haken-Mannigfaltigkeiten) Ausnahmen und keine Regeln sind.

Die Suche nach Beweisen für die Geometrisierungshypothese für andere Mannigfaltigkeiten als Haken-Mannigfaltigkeiten hat Mathematiker seit mehr als zwanzig Jahren ins Stocken gebracht. Schließlich legte Perelman 2002 seinen Beweis vor, der auf Bereichen der Mathematik basiert, die weit entfernt von denen sind, die von den meisten Anhängern von Thurston untersucht wurden. (Es sieht so aus, als hätte Perelmans Beweis auch die hundertjährige Hypothese von Poincare berührt, die dazu führte, dass Clay's Mathematics Institute ihm 2010 einen Millionen-Dollar-Preis anbot - den er aus komplexen Gründen sofort ablehnte.)

Perelmans Beweis war ein Wendepunkt, der, wie Thurston träumte, Topologie und Geometrie kombinierte. Jetzt hat jedes topologische Problem, das mit 3-Mannigfaltigkeiten verbunden ist, ein geometrisches Paar und umgekehrt. Perelmans Theorem ließ jedoch viele wichtige Fragen offen, welche Arten von 3-Mannigfaltigkeiten existieren können.

Durch die Klassifizierung kompakter 2-Mannigfaltigkeiten (Flächen) konnten Mathematiker nicht nur zeigen, dass jede Oberfläche mit einer geometrischen Struktur ausgestattet werden kann, sondern auch eine vollständige Liste aller möglichen 2-Mannigfaltigkeiten erstellen. In drei Dimensionen fehlte eine solche Liste schmerzlich.

Sieben von acht dreidimensionalen Geometrien - alle außer hyperbolisch - waren bekannt, und bereits vor Perelmans Arbeit stellten Topologen eine vollständige Beschreibung der Arten von Mannigfaltigkeiten zusammen, die eine dieser sieben Geometrien zulassen. Diese Formen sind relativ einfach und wenige.

Aber wie bei Oberflächen stellte sich in drei Dimensionen heraus, dass die meisten Verteiler hyperbolisch sind. Und die Abdeckung einer Vielzahl von Möglichkeiten hyperbolischer 3-Mannigfaltigkeiten war unter Mathematikern viel schlechter als bei den anderen sieben Geometrien.

"Von den acht Arten von Geometrien sind hyperbolische Mannigfaltigkeiten die mysteriösesten und reichsten", sagte Nicolas Bergeron von der Universität Pierre und Marie Curie in Paris.

Perelmans Ergebnis sagte den Mathematikern, dass hyperbolische Mannigfaltigkeiten die letzte Grenze waren - die einzige Art von 3-Mannigfaltigkeit, die noch zu verstehen war. Aber er sagte ihnen nicht, wie diese hyperbolischen Formen aussehen.

Titelgeschichte

Wieder einmal konnten sich Mathematiker an Thurstons Arbeit wenden, um sich beraten zu lassen. Seine berühmte Liste von Fragen enthielt viele Hypothesen über die Eigenschaften hyperbolischer 3-Mannigfaltigkeiten, darunter zwei Hypothesen, die in direktem Zusammenhang mit ihrem Aussehen standen: die Hypothese „Virtuelle Haken“ und die Hypothese „Virtuelles Bündel“.

Die virtuelle Hypothese von Haken (HHC) besagt, dass jede kompakte hyperbolische 3-Mannigfaltigkeit in gewissem Sinne fast eine Haken-Mannigfaltigkeit ist: Es ist möglich, die Mannigfaltigkeit in eine Haken-Mannigfaltigkeit umzuwandeln, indem ihre endliche Anzahl auf eine bestimmte Weise erweitert wird. Dieser neue entfaltete Verteiler wird als "endliche Abdeckung" des ursprünglichen Verteilers bezeichnet.

Mathematiker sagen, dass eine Sorte N eine andere Sorte M abdeckt, wenn es grob gesagt möglich ist, N eine bestimmte Anzahl von Malen (möglicherweise unendlich) um M zu wickeln, so dass jeder Teil von M so oft abgedeckt wird wie die anderen. Um eine Abdeckung zu sein, muss diese Umhüllung eine Reihe anderer Eigenschaften haben - zum Beispiel darf sich N nicht auf sich selbst biegen oder während der Umhüllung reißen. Jedes Stück von M ist mit einem Bündel identischer Kopien in N bedeckt.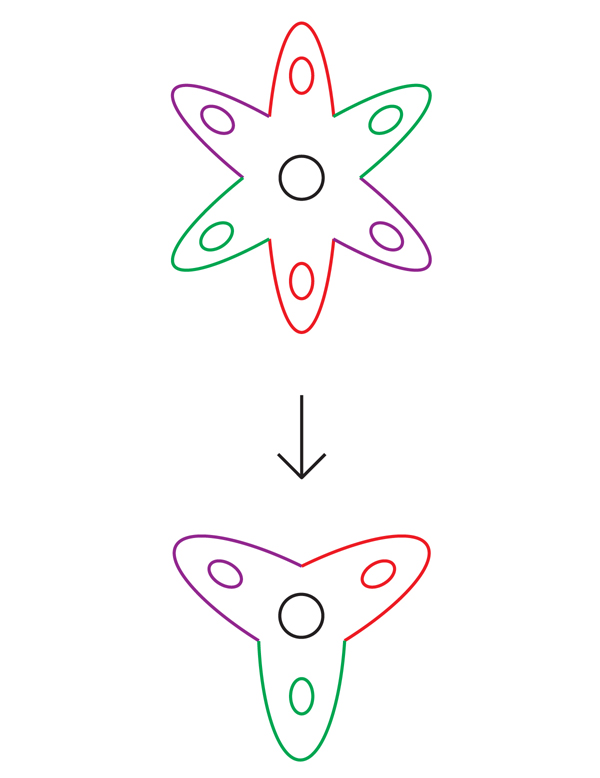

Abb . 5

Zum Beispiel bedeckt die Blume mit sechs Blütenblättern in Abb. 5 eine Blume mit drei Blütenblättern: Wickeln Sie die Blume mit sechs Blütenblättern einfach zweimal um das Blütenblatt mit drei Blütenblättern. Jeder Punkt mit drei Blütenblättern ist mit zwei Punkten mit sechs Blütenblättern bedeckt. Mathematiker nennen dies eine zweischichtige Beschichtung.

Ebenso bedeckt ein unendlicher Zylinder den Torus: Wickeln Sie den Zylinder einfach unendlich oft um den Torus (Abb. 6). Jeder Punkt des Zylinders ist abgedeckt: Schleife A wird von einem unendlichen Satz von Schleifen abgedeckt, die gleichmäßig über den Zylinder verteilt sind, und Schleife B wird auf dem Zylinder in einer entlang verlaufenden Linie eingesetzt.

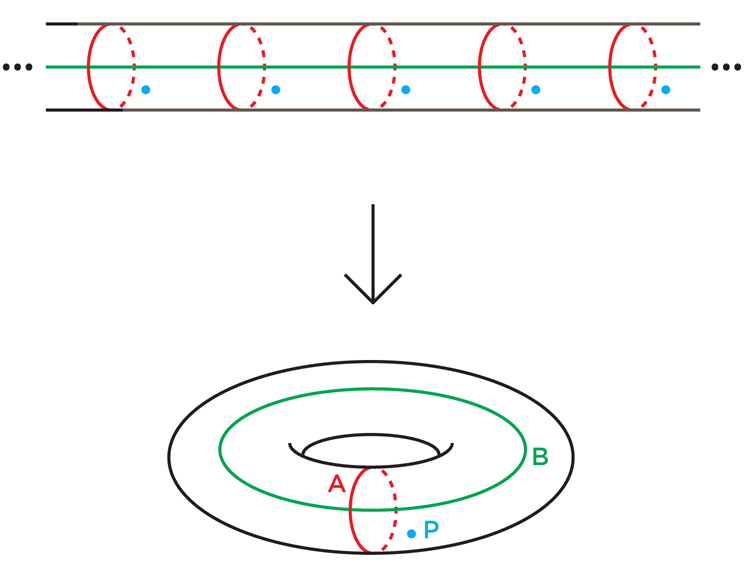Abb. 6 Die

Topologien der Vielfalt und ihre Abdeckung sind eng miteinander verbunden. Um einen Verteiler aus einer n-Schicht-Beschichtung wiederherzustellen, müssen Sie die Beschichtung nur n-mal selbst falten. Und umgekehrt, um die Beschichtung anhand der Sorte nachzubilden, schneiden Sie sie, machen n Kopien und kleben sie entlang der Ränder zusammen (die Betonbeschichtung, die Sie erhalten haben, hängt von der Wahl der Klebereihenfolge ab).

Eine Abdeckung bewahrt einige topologische Eigenschaften einer Mannigfaltigkeit und zeigt andere. Ein unendlicher Zylinder erinnert sich beispielsweise daran, dass die Schleife A am Torus geschlossen ist, vergisst jedoch, dass auch die Schleife B geschlossen ist.

Dieser Bereitstellungsprozess führte Thurston zu der Hoffnung, dass es für eine 3-Mannigfaltigkeit möglich ist, mit einer endlichen Anzahl von Schichten zu bedecken, die eine Haken-Mannigfaltigkeit sein werden. Wir haben bereits darauf hingewiesen, dass man nicht erwarten sollte, dass ein beliebiger kompakter hyperbolischer 3-Verteiler ein Haken-Verteiler ist (dass er eine eingebaute inkompressible Oberfläche hat). 1968 schlug der deutsche Mathematiker Friedhelm Waldhausen vor, dass eine solche Mannigfaltigkeit zumindest eine inkompressible Oberfläche enthalten sollte, obwohl sie durch sich selbst hindurchtreten und nicht eingebettet werden kann.

Wenn ja, argumentierte Thurston, könnte es eine endgültige Beschichtung geben, bei der sich die Oberfläche auf eine Weise entfaltet, die alle Selbstüberschneidungen beseitigt. Fertige Beschichtungen werden auf diese Weise häufig vereinfacht. Da zum Beispiel die Kurve in der Blume mit drei Blütenblättern in Fig. 7 zweimal um das zentrale Loch verläuft, kann keine Dehnung und Verschiebung dazu führen, dass sie sich nicht mit sich selbst schneidet. Wenn wir diese Kurve jedoch ab einem bestimmten Punkt P auf eine Blume mit sechs Blütenblättern drehen, wird die resultierende rote Kurve (die von Mathematikern als "Anstieg" der ursprünglichen Kurve bezeichnet wird) nur einmal um das zentrale Loch herumgehen und sich nicht mit sich selbst schneiden. (Es gibt auch einen zweiten Anstieg, eine blaue Kurve, die an zwei Punkten das Rot kreuzt und den Schnittpunkt in einer Blume mit drei Blütenblättern schließt.)

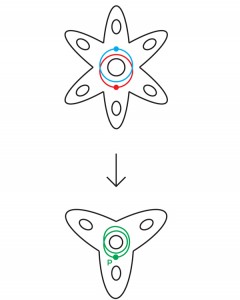Abb. 7

In einer Arbeit von 1982 schlug Thurston vor, dass es bei einem kompakten hyperbolischen 3-Verteiler eine Möglichkeit geben muss, ihn so zu erweitern, dass wir Oberflächen in die endliche Abdeckung eingebettet haben - das heißt, der 3-Verteiler sollte „praktisch Haken“ sein.

Wie wir bereits gesehen haben, kann eine Haken-Mannigfaltigkeit konstruiert werden, indem die Grenzen der Flächen eines Polyeders auf eine bestimmte Weise geklebt werden. Das VGH impliziert, dass jeder kompakte hyperbolische 3-Verteiler konstruiert werden kann, indem zuerst das Polyeder richtig geklebt und dann die resultierende Form endlich oft um sich selbst gewickelt wird.

Thurston ging noch strenger davon aus, dass jede kompakte hyperbolische 3-Mannigfaltigkeit virtuell geschichtet werden kann, dh eine endlich geschichtete Abdeckung aufweist. Eine Sorte, die sich „über einen Kreis schichtet“ (wie Mathematiker sagen), entsteht durch leichtes Verdicken der Oberfläche, wodurch sie dreidimensional wird, und Zusammenkleben der inneren und äußeren Ränder auf eine Weise, die eine reibungslose Verbindung der Oberflächen an jedem Punkt gewährleistet. (Ein solches Kleben ist im gewöhnlichen Raum ohne den Schnittpunkt der Teile der resultierenden Mannigfaltigkeit nicht möglich, kann aber abstrakt noch untersucht werden). Die Schichtung von Mannigfaltigkeiten soll sein, weil man sich vorstellen kann, wie eine verdickte Oberfläche so gedehnt wird, dass die Grenzflächen weit voneinander abweichen,und dann entfalten und vor dem Kleben aufeinander zu ziehen, und die resultierende Sorte ähnelt einem Armband mit einer unendlich dünnen Perle in Form einer Oberfläche an jedem Punkt des Armbandfadens. Diese Perlen sind Schichten.

Jeder Schichtverteiler ist ein Hakenverteiler, aber nicht umgekehrt. Daher ist die Hypothese von virtuellen Bündeln stärker als die von VGH, und Thurston war sich nicht sicher, ob dies wahr ist. "Diese fragwürdige Frage hat offenbar eine eindeutige Chance, eine positive Antwort zu erhalten", ist alles, was er 1982 in einem Werk schreiben konnte.

Thurston erklärte die VGH zunächst in einem frühen Versuch, sich seiner Geometrisierungshypothese zu nähern, die er bereits für Haken 3-Mannigfaltigkeiten bewiesen hatte. Wenn die VGH wahr wäre und jeder kompakte 3-Verteiler eine endliche Haken-Abdeckung wäre, wäre es vielleicht (Thurston hoffte) möglich, die geometrische Abdeckungsstruktur zu verwenden, um die geometrische Struktur des ursprünglichen Verteilers zu konstruieren.

30 Jahre später, viel später als Perelman die Geometrisierungshypothese mit völlig anderen Methoden bewies, blieben die VGH- und die virtuelle Bündelhypothese unbewiesen. Sie blieben zusammen mit zwei anderen Hypothesen die einzigen unbeantworteten Fragen von 23. Computerberechnungen sprachen für die Gültigkeit der VGH - Haken's endliche Bedeckungen wurden für jede der 10.000 computerausgewählten hyperbolischen 3-Mannigfaltigkeiten gefunden. Diese Arbeit wurde von Thurston und Nathan Dunfield von der University of Illinois in Urbana-Champaign durchgeführt. Aber Computer-Busting ist kein Beweis.

„Als Thurston diese virtuelle Haken-Hypothese aufstellte, schien diese Frage einfach zu sein. Aber er widersetzte sich hartnäckig der Entscheidung, die Aufschluss darüber gab, wie wenig wir in diesem Bereich verstehen, sagte Minsky. "Es stellte sich heraus, dass unsere Unwissenheit in diese Richtung tief war."

Gebäudeflächen

Im Jahr 2009 wurde das trübe Wasser rund um den Wasser-Wasser-Speicher gereinigt. In diesem Jahr kündigten Markovich und Jeremy Kahn, die damals an der Stony Brook University arbeiteten, den Beweis für einen wichtigen Schritt zum Nachweis des VHC an. Das Ergebnis, das wir als „Theorem auf inkompressiblen Oberflächen“ bezeichnen werden, postuliert, dass jede kompakte hyperbolische 3-Mannigfaltigkeit eine inkompressible Oberfläche enthält (die sich möglicherweise mit sich selbst schneidet und nicht eingebettet ist).

Der Beweis von Kan und Markovich ist eines der zentralen Beispiele für das Zusammenspiel von dreidimensionaler Topologie und Geometrie: Der Satz über inkompressible Oberflächen ist eine rein topologische Aussage, aber Kan und Markovich verwendeten aktiv eine andere Struktur aus der hyperbolischen Geometrie, um dies zu beweisen.

Um die Oberfläche innerhalb der 3-Mannigfaltigkeit zu konstruieren, verwendeten Kahn und Markovich die Eigenschaft hyperbolischer Formen, die als „exponentielles Mischen“ bezeichnet werden. Dies bedeutet, dass, wenn Sie einen Pfad irgendwo in einem kleinen Bereich innerhalb des Verteilers beginnen, eine Richtung wählen und sich vorstellen, dass sich Ihr Bereich entlang des Flusses in ungefähr der ausgewählten Richtung bewegt, sich Ihr Bereich allmählich ausbreitet und sich um einen 3-Verteiler wickelt zu jedem möglichen Ort aus jeder möglichen Richtung. Darüber hinaus wird es sehr schnell im exakten "exponentiellen" Sinne gehen.

Die Mischeigenschaft ist für hyperbolische 3-Mannigfaltigkeiten einzigartig und wächst grob gesagt aus der Tatsache, dass im Gegensatz zu euklidischen Räumen in einem hyperbolischen Raum „gerade Linien“ oder Geodäten relativ zueinander gebogen sind. Wenn Sie einen kleinen Bereich einer hyperbolischen Scheibe auswählen und zulassen, dass sie sich in die ausgewählte Richtung bewegt, wächst sie exponentiell schnell. Innerhalb eines kompakten 3-Verteilers wächst auch die Wachstumsregion exponentiell, aber da die Größe des Verteilers endlich ist, wird sich dieser Bereich schließlich immer wieder um ihn wickeln und sich viele Male überlappen. Darüber hinaus - und dies ist bereits schwieriger zu beweisen - wird sich der Bereich gleichmäßig um den Verteiler wickeln und alle Punkte mit ungefähr derselben Frequenz durchlaufen.

Mathematiker haben sich vor mehr als 25 Jahren mit dieser Eigenschaft der exponentiellen Vermischung befasst und die Statistiken dieses „geodätischen Flusses“ sorgfältig untersucht, nachdem sie ungefähr herausgefunden hatten, wann und wie oft ein bestimmtes Gebiet an einem bestimmten Punkt passieren wird. Aber bis Kahn und Markovich den Satz der inkompressiblen Oberfläche richtig aufgegriffen hatten, konnten Mathematiker diese Eigenschaft nicht verwenden, um topologische Strukturen in einer Mannigfaltigkeit zu konstruieren (ein anderer Mathematiker, Lewis Bowen von der Texas A & M University, versuchte, exponentielles Mischen für zu verwenden Konstruktion inkompressibler Oberflächen in 3-Mannigfaltigkeiten, aber seine Arbeit stieß auf technische Hindernisse).

Um zu sehen, wie die Eigenschaft des exponentiellen Mischens zum Aufbau topologischer und geometrischer Strukturen beiträgt, wenden wir sie auf eine einfachere Aufgabe an als das Bauen von Oberflächen: Konstruieren einer geschlossenen geodätischen Schleife, deren Länge nahe an unserer bevorzugten großen Zahl liegt (wir bezeichnen sie mit R).

Um eine Schleife zu bilden, wählen wir einen beliebigen Startpunkt im Verteiler und eine beliebige Anfangsrichtung aus und schalten dann einen imaginären Bewässerungsschlauch ein, der sich in einem kleinen Bereich einschließlich des Startpunkts befindet, und richten ihn grob in die ausgewählte Richtung. Wassertropfen fliegen entlang des geodätischen Pfades, und solange R groß genug ist, bedeutet das Mischen der Strömung, dass sich die Tropfen, wenn sie die Strecke R überschritten haben, ungefähr gleichmäßig über die gesamte Sorte verteilen. Insbesondere muss mindestens ein Tropfen in den Bereich des Startpunkts zurückkehren. Dann bauen wir einfach eine kleine Brücke, die die Geodät dieses Abfalls mit dem Startpunkt verbindet, um eine Schleife zu erhalten, die mit einer Länge von ungefähr R nahezu perfekt geodätisch ist. Es ist leicht zu zeigen, dass durch Festziehen dieser Schleife am VerteilerSie können die perfekte geodätische Schleife erhalten.

Beachten Sie, dass die Methode mehr als eine geodätische Schleife in der Nähe von R liefert. In diesem Prozess können Sie einen beliebigen Startpunkt und eine beliebige Richtung verwenden, sodass Sie viele solcher Schleifen erstellen können. Dies ist das Grundprinzip für den Aufbau von Strukturen durch exponentielles Mischen.

Exponentielles Mischen "behauptet, dass Sie unabhängig davon, welche Strukturen in der Vielfalt Sie finden, in ausreichenden Mengen gefunden werden", sagt Kalegari.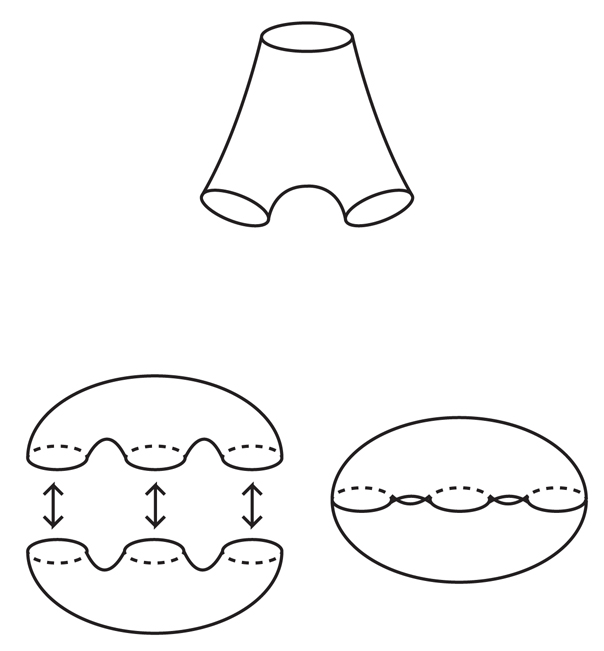

Abb. 8

Kan und Markovich verwendeten einen ähnlichen Ansatz wie in unserer Übung, um „Hosen“ zu erstellen - Oberflächen, die topologisch einer Kugel mit drei Löchern entsprechen (sozusagen eines für den Gürtel und zwei für die Beine). Diese Hosen sind das Ausgangsmaterial für die Konstruktion aller kompakten Oberflächen mit Ausnahme der Kugel und des Torus. Wenn Sie beispielsweise zwei Hosen kleben (oder nähen), erhalten Sie einen doppelten Torus (Abb. 8).

Kan und Markovich haben gezeigt, dass es für jede ausreichend große Anzahl R möglich ist, viele Paare solcher Hosen innerhalb des Verteilers zu konstruieren, dass sich ihre drei „Manschetten“ der Länge von R nähern und fast vollständig geodätisch sind, dh jedes Stück der Oberfläche der Hose sieht fast gleich aus Ansicht der hyperbolischen Geometrie.

Sie zeigten auch, dass Hosen für jede Manschette eine andere Hose haben, die von der Manschette in ungefähr die entgegengesetzte Richtung verläuft. Kahn und Markovic nähten diese Hosen an den Manschetten zusammen und erhielten eine große Familie kompakter Oberflächen, fast vollständig geodätisch, mit kleinen Falten an den Nähten. Fast geodätische Oberflächen sind in ihren 3-Mannigfaltigkeiten inkompressibel, daher hat die Konstruktion von Kan und Markovich den Satz inkompressibler Oberflächen bewiesen.

Diese Methode zeigte auch, dass eine 3-Mannigfaltigkeit nicht nur eine inkompressible Oberfläche hat, sondern „eine reiche Struktur von fast geodätischen Oberflächen an verschiedenen Orten“, sagt Kalegari.

Die Arbeit von Kahn und Markovich brachte ihnen den Preis des Clay Institute of Mathematics 2012 ein, der für mathematische Durchbrüche verliehen wurde.

"Die Techniken von Kahn und Markovich sind im Interesse ihrer Ergebnisse nicht minderwertig, und diese Arbeit wird zweifellos viele andere damit verbundene Forschungsbereiche inspirieren", sagte Jeffrey Brock von der Brown University in einem Artikel aus dem Jahr 2011 voraus.

Versteckte Struktur

Kan und Markovich schufen den Ausgangspunkt für Mathematiker, die versuchen, den VHC zu beweisen.

Sie zeigten, dass jeder Verteiler garantiert eine inkompressible Oberfläche enthält. Diese Oberfläche kann jedoch möglicherweise an vielen Stellen durch sich selbst hindurchgehen und nicht eingebettet werden. Um die VGHYU auf der Grundlage der Arbeit von Kan und Markovich zu erhalten, mussten Mathematiker eine endliche Abdeckung der Mannigfaltigkeit finden, bei der die Oberfläche genau wie im Beispiel mit sechs- und dreiblättrigen Farben auf eine Reihe von Oberflächen ansteigt, die sich nicht schneiden (obwohl sie sich schneiden können). Wenn es möglich wäre, wäre jede von ihnen eine eingebaute inkompressible Oberfläche in der Beschichtung, was bedeutet, dass die Beschichtung Haken wäre.

Aber wie findet man eine solche Berichterstattung?

„Es gibt eine große Lücke zwischen der Arbeit von Kahn und Markovic und dem WHC“, sagt Danfield. "Ihre Entdeckung war wichtig, aber es war unklar, ob sie bei der Suche nach eingebetteten Oberflächen helfen würde."

Die Arbeit von Kahn und Markovich erregte die Aufmerksamkeit von Daniel Wise von der McGill University. Wise machte eine Karriere in der Forschung zur Entfernung von Selbstüberschneidungen topologischer Objekte mit endlichen Bedeckungen, arbeitete jedoch im Kontext von „kubischen Komplexen“, Objekten, die sich auf den ersten Blick stark von 3-Mannigfaltigkeiten unterscheiden. Die Arbeit von Kahn und Markovich half Wise, anderen Mathematikern zu zeigen, dass diese beiden Kontexte nicht so unterschiedlich sind.

Der kubische Komplex - es ist der kubische Komplex (CC): Es handelt sich um eine Menge von Würfeln. Dort wird nicht nur ein dreidimensionaler Würfel als „Würfel“ bezeichnet, sondern auch eine Form in einer beliebigen Anzahl von Dimensionen, die aus allen Punkten besteht, deren Koordinaten beispielsweise auf den Intervallen zwischen - liegen. 1 und +1. Ein Quadrat ist beispielsweise ein zweidimensionaler Würfel und ein Segment ist eindimensional. Würfel im Raumschiff sind entlang Ecken, Kanten, Flächen und Seiten höherer Dimensionen miteinander verbunden.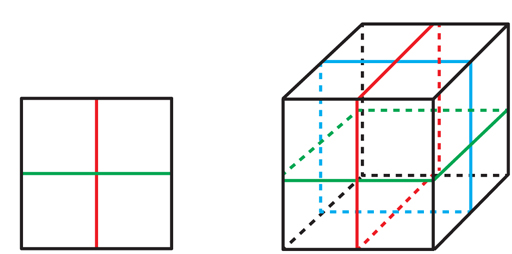

Abb. 9

CC unterscheidet sich stark von 3-Verteilern - sie sind nicht einmal Verteiler, da die Schnittpunkte zweier Würfel unterschiedlicher Abmessungen nicht dem üblichen Raum einer der Abmessungen ähneln. CCs sind jedoch vereinfachte Objekte, bei denen ein Schlüsselaspekt der in 3-Mannigfaltigkeiten enthaltenen Oberfläche untersucht wird: die Tatsache, dass eine solche Oberfläche ihre Umgebung zumindest lokal in zwei Teile unterteilt.

Wenn Sie Objekte untersuchen müssen, die die Form in zwei Teile teilen, sind Würfel das natürliche Startfeld. Aufgrund aller möglichen Formen haben sie das einfachste dieser Objekte: Hyperebenen, die sie in der Mitte schneiden. Das Quadrat hat zwei Hyperebenen (GP) - vertikale und horizontale Linien, die es halbieren. Der Würfel hat drei GPs (siehe Abb. 9). Ein n-dimensionaler Würfel hat n GP, das sich in seiner Mitte schneidet.

„Hyperebenen ähneln Oberflächen in 3-Mannigfaltigkeiten, aber man sieht sie sofort“, sagt Wise. "Es ist schwer, nach Oberflächen zu suchen, aber Hyperebenen stehen Ihnen von Anfang an zur Verfügung."

Wenn wir mit einem GP in einem Cube in einer Qualitätskontrolle beginnen, gibt es genau eine Möglichkeit, einen GP zu einem GP in benachbarten Cubes zu erweitern. Danach gibt es genau einen Weg, sie auf benachbarte zu erweitern. usw. Daher gibt es für jeden anfänglichen GP im CC eine einzigartige Möglichkeit, ihn auf den GP im gesamten CC auszudehnen (siehe 10).

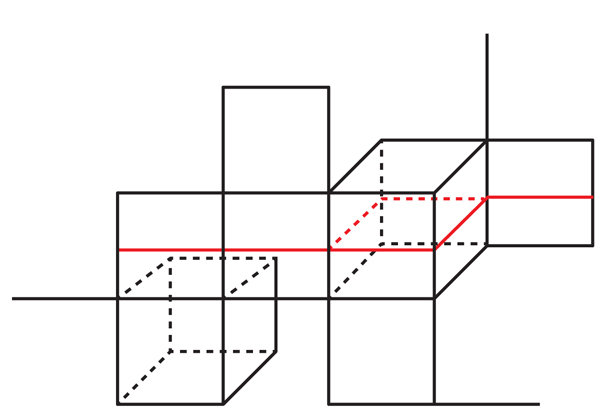Abb. 10. Die rote Hyperebene im Quadrat ganz rechts erweitert sich eindeutig zu einer Hyperebene im gesamten kubischen Komplex.

Diese Qualität steht in starkem Kontrast zu 3-Verteilern, bei denen eine kleine Oberfläche auf vielfältige Weise auf die gesamte Oberfläche ausgedehnt werden kann. CC mit ihren Hausärzten ist "schön, kristallklar und streng", sagt Eigol, und sie haben nicht die "Schlaffheit" von 3-Mannigfaltigkeiten und ihren Oberflächen.

Wenn wir den GP im Raumschiff erweitern, kann er auf den Würfel stoßen, von dem aus alles gestartet ist, und ihn senkrecht zum ursprünglichen GP passieren (siehe Abb. 11). Mit anderen Worten, eine erweiterte GPU muss nicht unbedingt eingebaut sein. Wie bei Oberflächen innerhalb von 3-Mannigfaltigkeiten kann man sich fragen, ob die Qualitätskontrolle eine endliche Abdeckung hat, in der diese sich selbst überschneidenden Hausärzte zu eingebetteten Hausärzten aufsteigen - dies ist die Version der virtuellen Haken-Hypothese für KK.

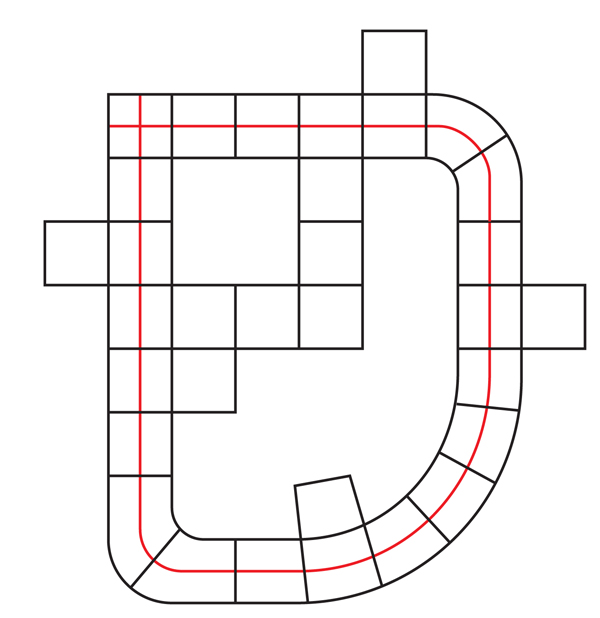Abb.11

Vor einigen Jahren haben Wise und Frédéric Haglund von der Universität Paris-Süd-XI eine Klasse von „speziellen“ QCs identifiziert, die neben anderen Eigenschaften nur über integrierte GPUs verfügen. In den letzten zehn Jahren hat Wise ein Arsenal von Techniken entwickelt, mit denen „spezielle QCs“ identifiziert werden können. Im Jahr 2009 veröffentlichte Wise ein 200-seitiges „Kernwerk“, wie Danfield es nannte, in dem er eine Reihe von Entdeckungen im Zusammenhang mit speziellen QCs beschrieb, wie beispielsweise „Kombinationssätze“, die zeigen, wie spezielle QCs zusammengestellt werden können, um neue QCs zu gewährleisten. auch eine "Spezialität" besitzen. In seiner Arbeit formulierte Wise eine Hypothese, die grob gesagt besagt, dass jede Qualitätskontrolle mit einer Geometrie, die sich ähnlich einer hyperbolischen Geometrie biegt, „praktisch“ speziell ist - das heißt, sie hat eine spezielle endliche Abdeckung. Diese Hypothese wurde die Wise-Hypothese genannt.

Wise war überzeugt, dass die QC-Struktur der Schlüssel zur Entdeckung vieler Eigenschaften des ursprünglichen Formulars sein wird, wenn dieses Formular in gewisser Weise der Qualitätskontrolle ähnelt - wenn es „gewürfelt“ werden kann.

"CC war ein Geheimnis, dass die Leute nicht einmal wussten, was sie fragen sollten", sagte er. "Dies ist eine grundlegende verborgene Struktur."

Kubische Wälder

Weise war äußerst besorgt über das Würfeln von Formen, aber zuerst lachten ihn seine Kollegen wegen dieser Manie aus.

Dann haben Kahn und Markovich den Satz der inkompressiblen Oberfläche bewiesen, und Wise und Bergeron haben sofort eine Arbeit veröffentlicht, die zeigt, dass die Existenz inkompressibler Oberflächen in einem kompakten hyperbolischen 3-Verteiler eine Methode zum Würfeln darstellt - und dass die Oberflächen des 3-Verteilers genau den Hyperebenen im resultierenden kubischen Komplex entsprechen .

Der Schlüssel zum Design von Wise und Bergeron war die Tatsache, dass Kahn und Markovich zeigten, wie man nicht eine, sondern viele Oberflächen konstruiert. Nach dem 2003 von Michael Sageev, der jetzt in Technion (Israel) arbeitet, erstmals formulierten Ansatz zum Würfeln nahmen Wise und Bergeron zunächst eine riesige Sammlung von Kahn-Markovich-Oberflächen - genug, um eine 3-Mannigfaltigkeit in kompakte Polygone zu unterteilen.

Stellen Sie sich nun einen der Schnittpunkte dieser Flächen vor - zum Beispiel befinden sich n Flächen darin. Sageevs Vermutung war, diesen Schnittpunkt sozusagen als Schatten vom Schnittpunkt von n Hyperebenen in einem n-dimensionalen Würfel zu betrachten. Ein KK, der einer 3-Mannigfaltigkeit entspricht, wird grob gesagt konstruiert, indem ein n-dimensionaler Würfel für jeden Schnittpunkt von n Oberflächen hinzugefügt wird (in Wirklichkeit wird all dies subtiler konstruiert, um verschiedene unvorhergesehene topologische Umstände zu berücksichtigen). Zwei Würfel in einem Komplex sind benachbart, wenn ihre entsprechenden Schnittpunkte in einem 3-Verteiler durch die Fläche eines der Polytope verbunden sind.

„Der kubische Komplex wird benötigt, um genau zu berechnen, wie sich Oberflächen untereinander und untereinander schneiden“, sagt Danfield.

Wise und Bergeron haben gezeigt, dass dieser KK „homotopisch äquivalent“ zum ursprünglichen Verteiler ist, dh der KK kann komprimiert und gedehnt werden (unter Berücksichtigung der Abflachung in einigen Dimensionen und des umgekehrten Prozesses), bis sich der KK in einen Verteiler verwandelt und umgekehrt. Darüber hinaus verwandelt diese homotope Äquivalenz jede Oberfläche eines 3-Verteilers in das entsprechende homotopieäquivalente GP in KK.

Die auf diese Weise konstruierte Qualitätskontrolle erfüllt die geometrischen Anforderungen der Wise-Hypothese. Wenn also die Wise-Hypothese zutrifft, hat diese Qualitätskontrolle eine endliche Abdeckung, in die alle Hausärzte eingebettet sind.

Wenn eine solche endgültige Beschichtung tatsächlich vorhanden ist (z. B. das Abdecken von m Blättern), müssen wir uns daran erinnern, dass die Beschichtung aus der Qualitätskontrolle selbst erstellt werden kann, indem sie auf besondere Weise geschnitten wird, dann m Kopien dieser Qualitätskontrolle erstellt und entlang der Schnittlinien zusammengeklebt werden. Es ist leicht zu zeigen, dass dieses Rezept für die Herstellung einer Beschichtung auf die Herstellung einer endgültigen Abdeckung eines 3-Verteilers übertragen werden kann und dass in dieser endgültigen Abdeckung die Kan-Markovich-Oberflächen, die zum Aufbau des CC verwendet werden, zu den eingebetteten Oberflächen aufsteigen. Mit anderen Worten, wenn die Wise-Hypothese wahr ist, dann ist auch die IHC wahr.

"Dies ist ein sehr seltsamer Kompromiss: Ihre Qualitätskontrolle kann beispielsweise 10.000-dimensional sein, und es scheint Ihnen, dass Sie die Situation in gewissem Sinne verschlechtern", sagt Wise. "Aber trotz des QC-Werts sind viele seiner Eigenschaften sehr leicht zu verstehen, daher ist dieses Verfahren sehr wertvoll." "Wir bevorzugen etwas Großes, aber gut organisiertes anstelle von 3-Mannigfaltigkeit."

Selbst nachdem Wise und Bergeron eine Verbindung zwischen QC und VGH hergestellt hatten, hielten sich die meisten Topologen, die 3-Mannigfaltigkeiten untersuchten, von QC fern. Vielleicht, weil Wises 200-seitige Arbeit entmutigend war oder weil CCs sich so sehr von ihren üblichen Räumen unterschieden.

„Diese Ideen waren zu esoterisch für Menschen, die aus der hyperbolischen Geometrie hervorgegangen sind“, sagt Bergeron.

Ein Mathematiker war jedoch bereits mit der Topologie der 3-Mannigfaltigkeiten sowie mit den abstrakteren kombinatorischen Dingen vertraut, die Wise in seinem Ansatz verwendete.

"Ich denke, Jan Eigol war der einzige Spezialist für 3-Mannigfaltigkeiten, der früh genug verstanden hat, wie Wises Ideen für die Topologie von 3-Mannigfaltigkeiten verwendet werden können", sagt Bergeron.

Eigol ging tiefer in das Studium von Wises "Hauptwerk" ein und war überzeugt, dass alle seine Teile, die mit Wises Hypothese zusammenhängen, korrekt waren. Aigol ist seit einiger Zeit an VHC beteiligt. Er erkannte, dass Wises Ansatz, schlaffe Oberflächen in kristalline Hyperebenen zu verwandeln, genau das war, was er brauchte.

"KK gibt uns Wälder für den Bau der endgültigen Beschichtung", sagte er.

Um eine spezielle Endbeschichtung auf dem Wise-Bergeron-Raumschiff zu erstellen, begann Aigol, das Raumschiff entlang des GP in „Lego-Würfel“ zu schneiden. Anschließend ordnete er den Flächen der Blöcke Farben zu, sodass zwei an der Ecke gefundene Flächen unterschiedliche Farben hatten. Dann zeigte Eigol, dass es grob gesagt eine Möglichkeit gibt, eine endliche Anzahl von Kopien von Lego-Würfeln auf Gesichter mit denselben Farben zu kleben, so dass auch die Farben an den Seiten dieser Gesichter übereinstimmen. Infolgedessen hat jeder erweiterte Allgemeinmediziner dieselbe Farbe. Die resultierende Qualitätskontrolle ist die endgültige Beschichtung des Originals, und alle seine GPs werden eingebettet, da zwei sich kreuzende GPs unterschiedliche Farben haben, sodass dies nicht ein GP ist, der sich selbst schneidet.

Am 12. März kündigte Aigol den Beweis der Wise-Hypothese und damit der virtuellen Haken-Hypothese an.

"Es war die aufregendste Nachricht, seit Perelman die Geometrisierungshypothese bewiesen hat", sagte Danfield.

Die Informationen gingen durch eine Gemeinschaft von Forschern mit 3 Mannigfaltigkeiten, und die Qualitätskontrolle wurde sofort zu einem gemeinsamen Thema für alle Topologen.

"Ich denke, dass die mathematische Gemeinschaft bisher nicht verstanden hat, wie mächtig Wises Arbeit ist", sagte Aigol. "Ich denke, mein Ergebnis wird den Menschen erklären, welche erstaunlichen Fortschritte er gemacht hat."

Jetzt, so Wise, beginnen Mathematiker zu begreifen, dass "jedes Mal, wenn Sie etwas kubieren, Sie alle möglichen Geheimnisse der Struktur enthüllen können".

Ende einer Ära

Aigols Beweis für Wises Theorie war der Beweis für "4 zum Preis von 1": Er bewies nicht nur den VHC, sondern auch die anderen drei von Thurstons 23 Fragen, die bis dahin offen blieben. In der Zeit vor dem Beweis zeigten Eigol und andere Mathematiker, dass alle drei dieser Fragen - die Hypothese des virtuellen Bündels und zwei weitere technische Fragen zu hyperbolischen 3-Mannigfaltigkeiten - auch aus der Wise-Hypothese folgten.

Im Fall der virtuellen Bündelhypothese erinnern wir uns, dass das Ziel darin bestand zu zeigen, dass jede kompakte hyperbolische 3-Mannigfaltigkeit eine endliche Bedeckung aufweist, die in einem Kreis gefasert ist, dh durch Kleben der gegenüberliegenden Teile einer verdickten Oberfläche konstruiert wird. Aus dem VGH wissen wir, dass ein Verteiler eine endliche Hakenov-Beschichtung hat - das heißt, die Beschichtung hat eine eingebaute inkompressible Oberfläche. Wenn Sie den Haken-Verteiler entlang dieser Oberfläche öffnen, erhalten Sie etwas, das an den Enden wie eine verdickte Oberfläche aussieht, aber wie Gott weiß, was in den "Eingeweiden" steckt.

Yang Aigol auf einer kürzlichen Reise nach Daejeon, Südkorea.

Laut Kalegari gab es 2008 einen „überraschenden Durchbruch“, als Eigol zeigte, dass hyperbolische 3-Mannigfaltigkeiten, die spezielle technische Bedingungen erfüllen, garantiert praktisch geschichtet sind. Im folgenden Jahr zeigte Wise auf dieser Basis, dass alle Haken-Mannigfaltigkeiten praktisch geschichtet sind. Das heißt, es gibt eine Möglichkeit, den Haken-Verteiler zu erweitern, um eine endliche Abdeckung zu erhalten, die eine komplexe Topologie enthüllt und zu einem einfachen folierten Verteiler führt. Wenn der Verteiler praktisch Hakenov ist, muss er daher virtuell geschichtet werden.

"Ich denke, jeder glaubte, dass die VGH wahr sein würde, aber die Hypothese des virtuellen Bündels schien uns weniger zugänglich zu sein", sagte Kalegari. "Für mich ist die Tatsache, dass die Hypothese der virtuellen Schichtung aus der VGH folgt, eine der schockierendsten Seiten dieser ganzen Geschichte."

Mit dem Beweis der Hypothese eines virtuellen Bündels „können Sie versucht sein und entscheiden, dass 3-Mannigfaltigkeiten zu einfach sind, weil Mannigfaltigkeiten, die in einem Kreis geschichtet sind, einfach sind“, sagte Minsky. "Aber ich denke, das lehrt uns, dass die Mannigfaltigkeiten, die in einem Kreis geschichtet sind, überhaupt nicht einfach und gerissener sind als wir erwartet hatten."

Gleichzeitig bedeutet der Satz des virtuellen Bündels, dass es ein einfaches und informatives Rezept für die Erstellung aller kompakten hyperbolischen 3-Mannigfaltigkeiten gibt: Beginnen Sie mit einer verdickten Oberfläche, kleben Sie den inneren und äußeren Rand mit Rotationen nach Ihrem Geschmack zusammen und falten Sie die Mannigfaltigkeit endlich oft auf sich selbst.

„Wenn Sie mich nach einem hyperbolischen 3-Verteiler fragen würden, würde ich fragen, welchen Typ Sie benötigen - welche Art von Bündel und endgültige Abdeckung? - sagt Kalegari. "Jetzt wissen wir, dass wir in diesem Prozess keinen einzigen 3-Verteiler verpassen."

Obwohl Mathematiker Zeit brauchen werden, um Eigols Arbeit gründlich zu testen, sind viele von ihnen optimistisch, dass sie den Test bestehen wird.

"Jan Aigol ist kein sorgloser Mensch", sagt Minsky.

Nachdem anscheinend die letzte Frage aus Thurstons Liste geklärt ist, fragen sich die Forscher, wie die Topologieregion der 3-Mannigfaltigkeiten in einer schönen neuen Welt nach Thurston aussehen wird.

Mathematiker sind sich einig, dass sie viel Arbeit haben werden, um nützliche Dinge zu finden, die QC für kubierbare Formen anbieten kann. Und für die 3-Mannigfaltigkeiten selbst ist laut Aigol das Ende der Ära gekommen - und der Beginn der nächsten.

„In den meisten Bereichen der Mathematik gibt es keinen Plan, der den Weg für die kommenden 20 bis 30 Jahre beschreiben könnte, wie es bei uns der Fall war“, sagt er. Nun, so schlägt er vor, könnte die Topologie von 3-Mannigfaltigkeiten und Geometrie anderen Bereichen der Mathematik ähneln, in denen Wissenschaftler auch ohne den Luxus eines großen hypothetischen Bildes von dem, was geschieht, berühren und Fortschritte machen.

"Neue Generationen von Mathematikern werden die folgenden wichtigen Fragen stellen", sagt Aigol.

Wir kommen in Form: von der hyperbolischen Geometrie zu kubischen Komplexen und umgekehrt