Informatiker haben einen fairen Kuchenalgorithmus für eine beliebige Anzahl von Menschen entwickelt

Zwei junge Wissenschaftler, Experten auf dem Gebiet der Informatik, fanden heraus, wie man ehrlich einen Kuchen zwischen einer beliebigen Anzahl von Menschen teilt, um das Problem zu lösen, mit dem Mathematiker seit Jahrzehnten zu kämpfen haben. Ihre Arbeit überraschte viele Forscher, die eine solche Trennung grundsätzlich für unmöglich hielten.

Das Teilen eines Kuchens ist eine Metapher für eine Vielzahl realer Aufgaben, einschließlich der Aufteilung eines bestimmten zusammenhängenden Objekts, sei es ein Kuchen oder ein Stück Land, zwischen Menschen, die seine Eigenschaften unterschiedlich schätzen. Einer mag einen Schokoladenüberzug, der andere will cremefarbene Blumen. Seit biblischen Zeiten ist ein Algorithmus bekannt, mit dem ein solches Objekt zwischen zwei Personen aufgeteilt werden kann, so dass niemand den anderen beneiden würde: Eine Person teilt den Kuchen für ihn in zwei gleiche Teile, und die andere wählt einen von ihnen aus. In der Genesis verwendeten Abraham (damals bekannt als Abram) und Lot diese Methode, um das Land zu teilen, als Abraham eine Trennung erfand und Lot zwischen Jordanien und Kanaan wählte.

1960- « » . , 1995 [Steven Brams] - [Alan Taylor] -. «» , – «», , , .

- , « , -, », [Ariel Procaccia], Informatiker an der Carnegie Mellon University, einer der Entwickler von Spliddit , einem kostenlosen Online-Tool für eine faire Aufgabenteilung, von Haushaltsaufgaben bis hin zu gemeinsamen Mietgebühren.

In den letzten 50 Jahren haben sich viele Mathematiker und Informatiker, einschließlich Procaccia, davon überzeugt, dass es keinen begrenzten fairen Algorithmus gibt, um einen Kuchen in n Teile zu teilen.

„Diese Aufgabe hat mich in den Bereich der gerechten Spaltungen geführt“, sagt Walter Stromkvist[Walter Stromquist], Professor für Mathematik am Brin Mavre College in Pennsylvania, der 1980 gute Ergebnisse beim Kuchen-Sharing-Problem erzielte. „Mein ganzes Leben lang dachte ich, ich würde in meiner Freizeit zu dieser Aufgabe zurückkehren und beweisen, dass eine solche Erweiterung des Ergebnisses im Prinzip unmöglich ist.“ .

Im April widerlegten jedoch zwei Informatikspezialisten diese Erwartungen, indem sie einen Algorithmus für faires Kuchen-Sharing mit einer Arbeitszeit veröffentlichten, die von der Anzahl der Teilnehmer am Sharing und nicht von ihren persönlichen Vorlieben abhängt. Ein Wissenschaftler, der 27-jährige Simon Mackenzie , Ph.D. aus Carnegie Mellon, präsentierte seine Arbeit am 10. Oktober auf den 57. jährlichen IEEE-Grundlagen der Informatik.

Der Algorithmus ist äußerst komplex. Eine Kuchenaufteilung zwischen n Teilnehmern kann bis zu n erfordern^{n n n n n} Schritte mit ungefähr der gleichen Anzahl von Schnitten. Selbst für eine kleine Anzahl von Teilnehmern übersteigt diese Anzahl die Anzahl der Atome im Universum. Laut einem zweiten Teammitglied, Haris Aziz , einem 35-jährigen Informatikspezialisten an der Universität von New South Wales, der in der australischen Datenforschungsgruppe Data61 arbeitet, haben Forscher bereits Ideen zur Vereinfachung und Beschleunigung des Algorithmus .

Experten, die laut Procaccia die Theorie der fairen Teilung studieren , halten dies für "definitiv das beste Ergebnis seit Jahrzehnten".

Kuchenstücke

Der Aziz- und Mackenzie-Algorithmus basiert auf einem eleganten Verfahren , das in den 1960er Jahren von den Mathematikern John Selfridge und John Conway unabhängig erfunden wurde und das es Ihnen ermöglicht, einen Kuchen fair in drei Teile zu teilen.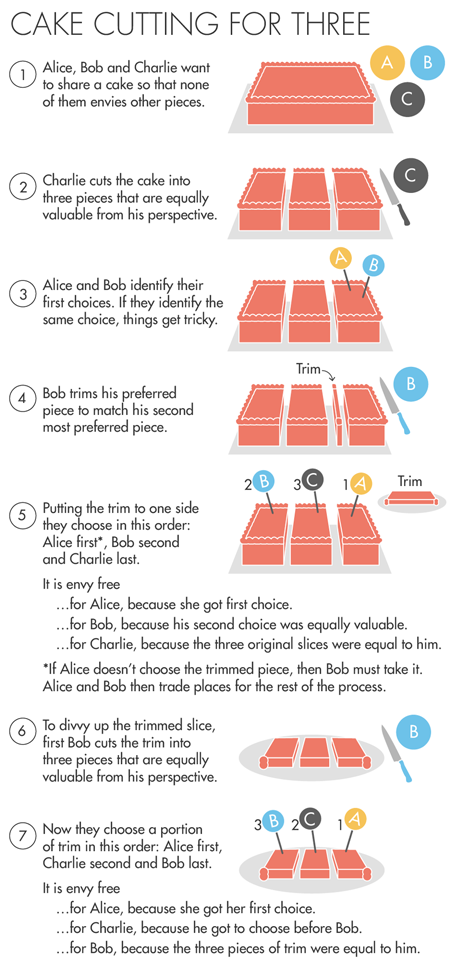



Wenn Alice, Bob und Charlie (A, B, C) den Kuchen teilen möchten, beginnt der Algorithmus damit, dass Charlie den Kuchen in drei Teile teilt, die für ihn gleich aussehen. Alice und Bob wählen die Stücke aus, die sie mögen. Wenn sie verschiedene Stücke wählen - voila, bekommt jeder, was er will.

Wenn Alice und Bob ein Stück auswählen, schneidet Bob einen kleinen Teil dieses Stücks ab, so dass das Stück aus seiner Sicht einem anderen Stück Kuchen entspricht - dem, das Bob an zweiter Stelle wählen würde. Der abgeschnittene Rückstand wird verschoben. Jetzt muss Alice aus den verbleibenden drei das beste Stück für sich auswählen und dann Bob auswählen - unter der Bedingung, dass er das von ihm geschnittene Stück nimmt, wenn Alice es nicht auswählt. Charlie bekommt das dritte Stück.

Infolgedessen beneidet niemand jemanden. Alice wählte die erste. Bob erhielt eines von zwei gleichwertigen Stücken. Charlie bekam eines der drei Originalstücke, die er selbst geschnitten hatte.

Es bleibt nur ein kleiner Ausschnitt übrig. Aber es kann geteilt werden, ohne zuerst den Algorithmus zu starten und ohne in einen endlosen Kreislauf von Beschneidungen und Entscheidungen zu geraten, da Charlie auf jeden Fall mit seinem Stück zufrieden ist - und selbst wenn derjenige, der das geschnittene Stück erhalten hat, den gesamten Rest im Anhang dazu erhalten hätte, z Charlie würde nicht unehrlich aussehen, weil das geschnittene Stück und der Rest ein Stück Kuchen ergeben, das seinem Stück entspricht - schließlich hat er diese Stücke von Anfang an geschnitten. Aziz und Mackenzie beschreiben Charlies Position als "dominant".

Wenn Alice zum Beispiel das geschnittene Stück bekommen hat, dann schneidet Bob die Verkleidung in drei Teile, was aus seiner Sicht äquivalent ist. Alice wählt eines dieser Stücke für sich selbst aus, dann wählt sie Charlie und dann Bob. Alle sind glücklich: Alice hat sich zuerst entschieden, Charlie bekommt ein Stück besser als Bob (und es ist ihm egal, wie viel Alice genommen hat), und aus Bobs Sicht sind alle drei Stücke gleichwertig.

Brahms und Taylor verwendeten die Eigenschaft "Dominanz" (jedoch mit einem anderen Namen), um ihren Algorithmus von 1995 zu entwickeln, aber sie beendeten ihre Idee erst, als ein begrenzter Algorithmus erschien. In den nächsten 20 Jahren hat niemand die besten Ergebnisse erzielt. "Und nicht wegen des Mangels an Versuchen", sagt Procaccia.

Unprofessionelle Kuchenteiler

Als Aziz und Mackenzie (A & M) vor ein paar Jahren beschlossen, diese Aufgabe zu übernehmen, waren sie neu in der Aufgabe des Kuchen-Teilens. "Wir hatten nicht so viel Erfahrung wie die Leute, die intensiv daran gearbeitet haben", sagte Aziz. "Obwohl dies normalerweise ein Nachteil ist, war es in unserem Fall ein Vorteil, weil wir anders dachten."

A & M untersuchte zunächst die Aufgabe, sich von Grund auf in drei Teilnehmer aufzuteilen, und kam als Ergebnis der Analyse zu einem begrenzten fairen Algorithmus für vier Teilnehmer , der von ihnen im letzten Jahr veröffentlicht wurde.

Sie konnten nicht sofort zeigen, wie sie ihren Algorithmus auf eine Anzahl von mehr als vier Teilnehmern erweitern konnten, aber sie nahmen diese Aufgabe begeistert an. „Nachdem wir die Arbeit mit vier Teilnehmern gesendet hatten, wollten wir die Arbeit wirklich schnell fortsetzen, bis jemand, der erfahrener und klüger ist, sie unabhängig auf den Fall von n Teilnehmern verallgemeinert“, sagt Aziz. Und nach ungefähr einem Jahr war ihre Suche erfolgreich.

Wie der Selfridge-Conway-Algorithmus bietet das AiM-Protokoll ständig verschiedenen Teilnehmern die Möglichkeit, den Kuchen in n gleiche Teile zu schneiden, und anderen, Kuchenstücke zu schneiden und auszuwählen. Es gibt aber auch andere Schritte im Algorithmus, zum Beispiel den periodischen Austausch von Kuchenstücken auf besondere Weise, um die Anzahl der dominanten Beziehungen zwischen den Teilnehmern zu erhöhen.

Diese Beziehungen ermöglichen es A & M, die Komplexität der Aufgabe zu reduzieren. Wenn zum Beispiel drei Teilnehmer den Rest dominieren, können sie bereits zum Essen ihrer eigenen Kuchenstücke geschickt werden - sie werden glücklich sein, unabhängig davon, wer die Reste bekommt. Danach bleiben weniger Teilnehmer übrig, und nach einer begrenzten Anzahl solcher Schritte sind alle zufrieden und der ganze Kuchen wird geteilt.

„Wenn man auf die Komplexität des Algorithmus zurückblickt, ist es nicht verwunderlich, dass die Entwicklung so lange gedauert hat“, sagt Procaccia. Die A & M glauben jedoch bereits, dass sie den Algorithmus vereinfachen können, so dass kein Austausch von Teilen erforderlich ist und in nur n ^{n n} Schritten erfolgt. Laut Aziz arbeiten sie bereits an diesen Ergebnissen.

Brahms warnt davor, dass selbst ein einfacherer Algorithmus keine praktische Anwendung finden wird - schließlich enthalten die Kuchenstücke, die die Teilnehmer erhalten, viele kleine Krümel aus verschiedenen Teilen des Kuchens. Dieser Ansatz ist nicht besonders nützlich, wenn Sie beispielsweise das Land teilen.

Für Mathematik- und Informatiker, die sich mit dem Problem befassen, setzt das neue Ergebnis „das gesamte Thema zurück“, sagt Stromkvist.

Nachdem die Forscher nun wissen, dass Kuchen in eine begrenzte Anzahl von Schritten unterteilt werden kann, besteht der nächste Schritt laut Procaccia darin, die große Lücke zwischen der Obergrenze für die Anzahl der Schritte nach der AiM-Methode und der Untergrenze für die Anzahl der dafür erforderlichen Schritte zu verstehen. Procaccia hat bereits früher bewiesen, dass der Algorithmus für die gerechte Trennung des Kuchens nicht weniger als n überschreiten kann² Schritte - aber die Anzahl der Schritte ist winzig im Vergleich zu n ^{n n n n n} und sogar n ^{n n} .

Laut Aziz müssen Forscher jetzt herausfinden, wie diese Lücke geschlossen werden kann. "Ich denke, dass Fortschritte in beide Richtungen erzielt werden können."