Vier-Bit-Papp- und Kugelrechner
Aussehen eines Vier-Bit-Papprechners aus Pappe. Der Halbaddierer oben und drei Addierer im mittleren und unteren Teil des Rechners sind deutlich sichtbar.Vor der Erfindung der Elektronik haben Menschen mechanische Computer aus improvisierten Materialien hergestellt. Das bekannteste und komplexeste Beispiel für eine solche Maschine ist der Antikythera-Mechanismus - ein komplexes Gerät mit mindestens 30 Gängen wurde verwendet, um die Bewegung von Himmelskörpern zu berechnen und das Datum von 42 astronomischen Ereignissen herauszufinden.Heutzutage sind mechanische Computer (Taschenrechner) eher ein Unterhaltungsobjekt für Geeks und eine Gelegenheit, eine lustige Show zu arrangieren. Zum Beispiel wie ein Computer mit 10.000 Domino-Kacheln , der beliebige vierstellige Binärzahlen addiert und eine fünfstellige Zwei-Bit-Summe erzeugt (mathematische Theorie dieses Rechners und der Architektur ). Solche Aufführungen ermöglichen es Kindern, besser zu verstehen, wie Bitlogikoperationen beim Programmieren funktionieren und wie Logikgatter angeordnet sind. Und im Allgemeinen ist es sehr interessant, aus improvisierten Materialien einen kleinen Computer mit eigenen Händen herzustellen, insbesondere wenn Sie dies mit Ihrem Kind tun.
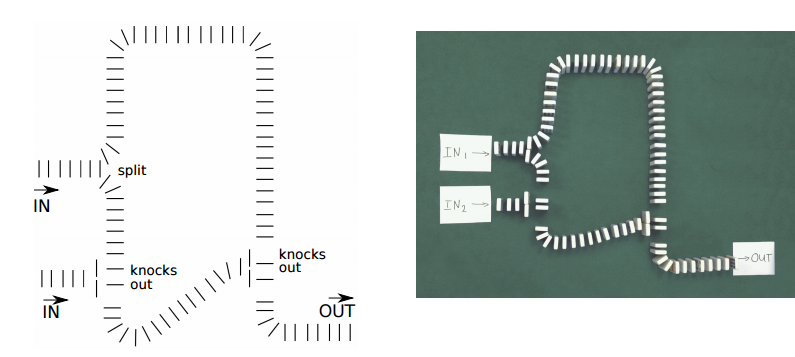Die logische UND-Verknüpfung in einem Computer mit 10.000 Domino-Kacheln.Für die Herstellung eines mechanischen Rechners ist der Lego-Konstruktor hervorragend. Auf YouTube finden Sie viele Beispiele für solche Taschenrechner .Lego ComputerrechnerInspiriert von einem Beispiel eines Computers aus Dominosteinen und mechanischen Taschenrechnern des Lego-Konstruktors beschloss der C ++ - Programmierer unter dem Spitznamen lapinozz zusammen mit seinen jüngeren Schwestern, zu Hause etwas Ähnliches für eines der schulwissenschaftlichen Projekte der Schwester zu bauen. Er konzipierte und implementierte einen voll funktionsfähigen 4-Bit- LOGIC- Rechner (Logic cardbOard Gates Inpredictable Calculator) . Um diesen Computer herzustellen, wird nichts außer Pappe und Kleber benötigt, und er funktioniert nicht mit Elektrizität, sondern mit Kugeln und Erdgravitation. Der Rechner kann Zahlen von 0 bis 15 mit maximal 30 hinzufügen.Im Gegensatz zu Lego-Domino-Fliesen und Lego-Steinen wurden bei der Herstellung dieses Rechners keine Fabrikkomponenten verwendet. Alle Elemente des Rechners werden von Grund auf aus Pappe geklebt, was auf den Fotos des Geräts gut verständlich ist. In diesem Sinne kann dieses Gerät als einzigartig angesehen werden.Projektziel
Visuelle Darstellung des Hinzufügens von Binärzahlen. Einem Schüler beibringen, wie man von dezimal nach binär und zurück übersetzt. Untersuchung von Bitlogikoperationen und grundlegenden Logikschaltungen.Aussehen des Rechners
Wie Sie auf dem Foto des Rechners sehen können, befindet sich im oberen Teil eine Zone zur Dateneingabe. Nach Abschluss aller logischen Operationen zeigen die Kugeln das Ergebnis der folgenden Operation.
Die Dateneingabe erfolgt durch Bälle. Der Ball ist - 1, der Ball ist nicht - 0. Das Bit rechts ist das kleinste Bit der Zahl. Vor Arbeitsbeginn sollten einige Teile des Rechners in ihre ursprüngliche Position gebracht werden. Nach Angabe der Anfangswerte wird der Kartonstreifen zurückgeschoben, der die Kugeln in der Ausgangsposition hält - und der Addiervorgang beginnt.Dies ist beispielsweise die Ausgangsposition der Kugeln für Operation 7 + 5 (0111 + 0101).
Taschenrechner
Die logischen Operationen eines Papprechners werden auf ähnliche Weise wie bei dem oben erwähnten Domino-Computer ausgeführt .Schematische Logikgatter für alle logischen Operationen sind im Diagramm dargestellt.
Das heißt, das logische Gatter "UND" (UND) bedeutet, dass, wenn 0 Kugeln am Eingang empfangen werden, 0 am Ausgang erhalten wird. Beim Empfang von 1 Kugel am Eingang wird 0 am Ausgang erhalten. Bei Erhalt von 2 Bällen am Eingang wird 1 am Ausgang erhalten.1 am Eingang, 0 am Ausgang
2 am Eingang, 1 am Ausgang
Das XOR-Logikgatter ist etwas komplizierter. In diesem Fall muss ein Ball passen, wenn er ankommt. Und wenn zwei Kugeln ankommen, müssen sie sich gegenseitig aufheben, das heißt, die Ausgabe ist 0. Der Autor zeigt, wie das geht, durch ein vertikal hängendes Stück Pappe mit einem schmalen Hals. Wenn zwei Bälle gleichzeitig ankommen, blockieren sie sich gegenseitig - und implementieren so effektiv die logische XOR-Operation.XOR-Logikgatter
Um das System zu optimieren und die Masse der UND- und XOR-Logikgatter nicht zu blockieren, hat der Autor einen Halbaddierer implementiert- eine kombinatorische Logikschaltung mit zwei Eingängen und zwei Ausgängen. Mit dem Halbaddierer können Sie die Summe von A + B berechnen, wobei das Ergebnis zwei Bits S und C sind, wobei S das Bit des Summenmoduls 2 und C das Übertragsbit ist. In unserer Kartonkonstruktion bedeutet dies, dass wenn wir 1 Ball am Eingang haben, dieser zum Ausgang C geht und wenn sich 2 Bälle am Eingang befinden, 1 Ball zum Ausgang S geht und der zweite nirgendwo hinkommt.Der Programmierer entwickelte ein ziemlich einfaches und effektives Schema für einen Halbaddierer. Darin setzt 1 Ball am Eingang ruhig seinen Weg fort, dreht die Barriere und geht in Loch C. Wenn jedoch zwei Bälle eintreten, kann der zweite Ball die Barriere nicht mehr passieren, die vom ersten Ball umgedreht wird - und fällt in das Loch und nagelt einen neuen Weg S. Dies ist ein Halbaddierer.Ein Ball am Eingang des Halbaddierers
Zwei Bälle am Eingang des Halbaddierers
Schließlich ist der Addierer ein echtes Meisterwerk. Normalerweise besteht es aus zwei Halbaddierern und einem logischen Gatter "ODER", aber der Autor hat ein anderes Design implementiert, das eigentlich eine kleine Modifikation des Halbaddierers ist.Eine Kugel am Eingang - eine Kugel am Weg 1
Zwei Bälle am Eingang - eine Kugel am Weg 2
Drei Bälle am Eingang - eine Kugel am Weg 1 und die andere entlang des Weges 2
Der gesamte Rechner besteht vollständig aus einem Halbaddierer und drei Addierern.
Der Rechner liefert das richtige Berechnungsergebnis, wenn die Bälle mit der richtigen Geschwindigkeit fallen, nicht zu schnell und nicht zu langsam, und nicht voneinander abprallen. Die Logik selbst ist fehlerfrei, aber in der Praxis ist der Taschenrechner manchmal fehlerhaft.Source: https://habr.com/ru/post/de399391/
All Articles