Mysteriöse Strukturen verbinden Mathematik und Natur

In der mexikanischen Stadt Cuernavaca erhöht ein "Spionagenetz" die Effizienz der Busflotte. Infolgedessen entspricht der Busfahrplan immer dem Muster der „Universalität“

Als der tschechische Physiker Petr Šeba 1999 an einer Bushaltestelle in Cuernavaca, Mexiko, saß, bemerkte er, dass Menschen Busfahrern Papierstücke gegen Geld gaben. Er stellte fest, dass dies keine Manifestation des organisierten Verbrechens war, sondern ein anderer „Schattenhandel“: Jeder Fahrer bezahlte einen „Spion“, der feststellte, wann der vorherige Bus die Bushaltestelle verließ. Wenn er kürzlich abreiste, wurde der Fahrer dieses Busses langsamer, damit sich die Passagiere an der nächsten Haltestelle versammeln konnten. Wenn dieser Bus vor langer Zeit abfuhr, beschleunigte der Fahrer, damit andere Busse ihn nicht überholten. Ein solches System maximierte die Gewinne der Fahrer. Was Sheba eine Idee gab.

"Wir dachten, wir beobachten eine Situation, die etwas an chaotische Quantensysteme erinnert", erklärte Shebas Co-Autor Milan Krbálek.

Nach mehreren erfolglosen Versuchen, mit den „Spionen“ zu kommunizieren, bat Sheba seinen Schüler zu erklären, dass er weder von der Steuer noch von der Mafia stamme. Er ist nur ein verrückter Wissenschaftler, der Tequila in ihre Daten umwandelt. Und die Leute gaben ihm ihre Notizen. Als die Forscher Tausende von Busabfahrtszeiten planten, wurde ihr Verdacht bestätigt. Die Wechselwirkung zwischen Fahrern führte zur Verteilung von Lücken zwischen Transportabfällen, was mit der Struktur einiger Experimente in der Quantenphysik zusammenfiel.

"Ich dachte, dass so etwas auftauchen könnte, aber ich war überrascht, einen so genauen Zufall zu sehen", sagte Sheba.

Subatomare Partikel haben mit einem dezentralen Bussystem wenig gemeinsam. Aber im Laufe der Jahre seit der Entdeckung seltsamer Quantenwechselwirkungen sind dieselben Datenstrukturen in anderen, nicht verwandten Situationen aufgetreten. Wissenschaftler glauben, dass dieses gemeinsame Phänomen, das als "Universalität" bekannt ist, auf der mathematischen Verbindung von Phänomenen beruht und ihnen hilft, komplexe Systeme vom Internet bis zum Klima des Planeten zu modellieren.


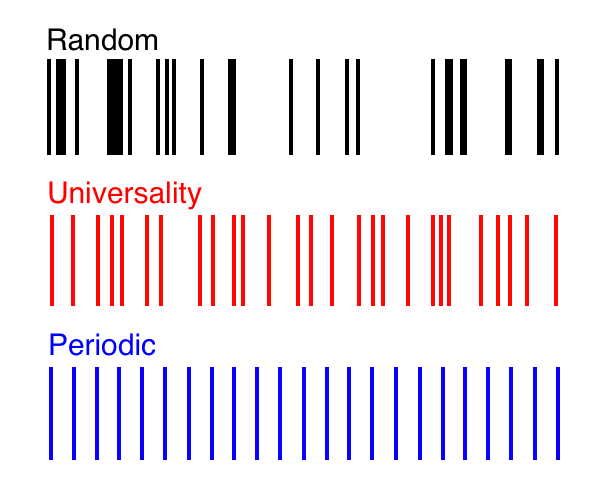Das rote Diagramm stellt das perfekte Gleichgewicht zwischen Zufälligkeit und Periodizität dar, das als Universalität bezeichnet wird. Es wird in den Spektren vieler komplexer Systeme mit Korrelation beobachtet. In diesem Spektrum gibt die mathematische Korrelationsfunktion die genaue Wahrscheinlichkeit des Vorhandenseins von zwei Linien in einem bestimmten Abstand voneinander an.

Eine solche Struktur wurde erstmals in den 1950er Jahren in der Natur gefundenEnergiespektrum eines Urankerns , eines Monsters mit Hunderten von beweglichen Teilen, das auf unendlich viele Arten oszilliert und sich ausdehnt und eine unendliche Folge von Energieniveaus abgibt. Im Jahr 1972 beobachtete Hugh Montgomery, ein Spezialist für Zahlentheorie, diese an den Nullen der Riemannschen Zeta-Funktion , einem mathematischen Objekt, das mit der Verteilung von Primzahlen zusammenhängt. Im Jahr 2000 fanden Krbalek und Sheba sie auf einem Busabfahrtsplan in Cuernavaca . Und kürzlich erschien es in den spektralen Messungen von Verbundwerkstoffen wie Meereis und menschlichem Knochengewebe sowie in der Dynamik der Signale des Erd-s-Reni-Modells , einer vereinfachten Version des Internets.

Jedes dieser Systeme hat ein Spektrum - eine Barcode-Sequenz, die Daten wie Energieniveaus, Zeta-Nullen, Busabfahrtszeiten oder Signalgeschwindigkeiten darstellt. Im gesamten Spektrum treten identische Strukturen auf. Die Verteilung der Daten sieht zufällig aus, aber gleichzeitig "stoßen" sich die benachbarten Linien gegenseitig ab, was zu einer gewissen Regelmäßigkeit der Lücken führt. Das genaue Gleichgewicht zwischen Chaos und Ordnung, das durch die Formel bestimmt wird, tritt auch bei rein mathematischen Problemen auf: Es bestimmt den Abstand zwischen den Eigenwerten einer mit Zufallszahlen gefüllten Matrix.

„Warum sich so viele physikalische Systeme wie Zufallsmatrizen verhalten, bleibt ein Rätsel“, sagt Horng Tzer Yao, Mathematiker an der Harvard University. "Aber in den letzten drei Jahren haben wir einen sehr wichtigen Schritt unternommen, um dies zu verstehen."

Um das Phänomen der Universalität in Zufallsmatrizen zu untersuchen, haben Wissenschaftler ein wenig Verständnis dafür, warum es überall auftritt und wie es verwendet werden kann. In einem Stapel neuer Arbeiten beschrieben Yao und andere Mathematiker viele neue Arten von Zufallsmatrizen, die verschiedenen numerischen Verteilungen und Symmetrieregeln entsprechen. Beispielsweise können die Zahlen für Spalten und Zeilen von Matrizen aus der Normalverteilungskurve möglicher Werte entnommen oder mit den Werten 1 und -1 gefüllt werden. Der obere rechte und untere linke Teil der Matrix spiegeln sich möglicherweise gegenseitig oder werden möglicherweise nicht angezeigt. Und unabhängig von ihren Eigenschaften zeigen Zufallsmatrizen die gleichen chaotischen, aber regelmäßigen Spektren in der Verteilung ihrer Eigenwerte. Daher nannten Mathematiker dieses Phänomen "Universalität".

"Es sieht aus wie ein Naturgesetz", sagte Wang Wu, ein Mathematiker an der Yale University, der zusammen mit Terence Tao von der University of California in Los Angeles die Universalität für eine breite Klasse von Zufallsmatrizen bewies.

Es wird angenommen, dass Universalität in sehr komplexen Systemen auftritt, die aus vielen Teilen bestehen, die eng miteinander interagieren, um ein Spektrum zu erzeugen. Eine Konfiguration erscheint beispielsweise im Spektrum einer Zufallsmatrix, weil alle Elemente der Matrix zur Berechnung dieses Spektrums verwendet werden. Aber zufällige Matrizen sind laut Wu einfach „Spielzeugsysteme“, sie sind einfach genug zu lernen und reich genug, um reale Systeme zu modellieren. Vielseitigkeit ist viel häufiger. Die Wigner-Hypothese (benannt nach Eugene Wigner, der Phyisis, die die Universalität im Spektrum der Atome entdeckte) legt nahe, dass alle komplexen Systeme mit Korrelation universell sind, vom Kristallgitter bis zum Internet.

Je komplexer das System ist, desto universeller manifestiert es sich, sagt Laszlo Erdös von der Universität München, einer der Arbeitskollegen von Yao. "Sie glauben, Universalität ist typisches Verhalten."

In vielen einfachen Systemen können einzelne Komponenten das Gesamtergebnis zu stark beeinflussen, was das Erscheinungsbild des Spektrums verändert. Größere Systeme haben keine Einzelkomponentendominanz. "Es stellt sich heraus, dass es einen Raum gibt, in dem sich viele Menschen für etwas entscheiden, und die Identität eines von ihnen ist nicht so wichtig", sagt Wu.


Mathematiker verwenden Zufallsmatrizen, um einige Eigenschaften des Internets zu untersuchen und vorherzusagen, beispielsweise die Größe eines typischen Computerclusters

Wenn ein System Universalität demonstriert, dient dies als Garantie dafür, dass es komplex ist und genügend Korrelation darin vorhanden ist, um als Zufallsmatrix interpretiert zu werden. "Das heißt, Sie können eine Zufallsmatrix verwenden, um sie zu modellieren", sagt Wu. "Sie können andere Modellparameter basierend auf der Matrix berechnen und sie verwenden, um das Verhalten dieses Systems vorherzusagen."

Diese Technik ermöglicht es Wissenschaftlern, die Struktur und Entwicklung des Internets zu verstehen. Einige Eigenschaften dieses riesigen Computernetzwerks, wie beispielsweise die typische Größe eines Computerclusters, können durch die gemessenen Eigenschaften der entsprechenden Zufallsmatrix ziemlich genau geschätzt werden. „Die Menschen interessieren sich für Cluster und ihren Standort, und dies ist häufig auf praktische Ziele wie Werbung zurückzuführen“, sagt Wu.

Ähnliche Technologien können zu Verbesserungen der Klimamodelle führen. Wissenschaftler haben herausgefunden, dass das Vorhandensein von Universalität, ähnlich dem Energiespektrum, im Material eine starke Verbundenheit seiner Teile und infolgedessen eine gute Leitfähigkeit von Flüssigkeiten, Elektrizität oder Wärme anzeigt. Und umgekehrt kann der Mangel an Vielseitigkeit auf eine Spärlichkeit des Materials und seiner Isoliereigenschaften hinweisen. In einem neuen Artikel, der auf einer mathematischen Konferenz in San Diego vorgestellt wurde, verwendeten Ken Golden, ein Mathematiker an der Universität von Utah, und sein Student Ben Murphy diesen Unterschied, um die Wärmeleitfähigkeit und den Flüssigkeitsfluss im Meereis sowohl auf mikroskopischer Ebene als auch auf mikroskopischer Ebene vorherzusagen Arktisches Wermut, das in Gebieten vorkommt, die sich über Tausende von Kilometern erstrecken.

Die spektrale Messung des Mosaiks aus geschmolzenem Wermut, fotografiert von einem Hubschrauber, oder die aus der Probe erhaltenen Meereisdaten zeigen den Status jedes dieser Systeme. „Der Flüssigkeitsfluss durch das Meereis treibt sehr wichtige Prozesse an, die verstanden werden müssen, um das Klimasystem zu verstehen“, sagt Golden. "Die Übergänge in der Statistik unserer eigenen Entscheidungen stellen einen neuen, mathematisch strengen Ansatz für die Einbeziehung von Meereis in Klimamodelle dar."

Der gleiche Trick kann zu einem einfachen Test auf Osteoporose führen. Golden, Murphy und ihre Kollegen stellten fest, dass das Spektrum eines dichten, gesunden Knochens vielseitig ist, das Spektrum eines porösen Knochens jedoch nicht.


Arktische Wermutwälder sind universell, wenn sie ausreichend miteinander verbunden sind

„Wir arbeiten mit Systemen, deren„ Partikel “Millimeter oder Kilometer groß sein können“, sagt Murphy über Systemkomponenten. "Es ist erstaunlich, dass die gleiche Mathematik sie alle beschreibt."

Der Grund, warum reale Systeme ein ähnliches Verhalten wie eine Zufallsmatrix zeigen, ist im Fall eines schweren Atomkerns vielleicht am einfachsten zu verstehen. Alle Quantensysteme, einschließlich Atome, arbeiten nach den Regeln der Mathematik, insbesondere unter Beteiligung von Matrizen. "Dies ist die Essenz der Quantenmechanik", sagt Freeman Dyson, ein ehemaliger mathematischer Physiker, der in den 1960er und 1970er Jahren am Princeton Institute for Advanced Engineering an der Entwicklung der Zufallsmatrixtheorie mitgewirkt hat. "Jedes Quantensystem wird durch eine Matrix beschrieben, die seine Gesamtenergie darstellt, und die eigenen Lösungen der Matrix sind die Energieniveaus des Quantensystems."

Matrizen einfacher Atome, Wasserstoff und Helium, können genau berechnet werden, und die erhaltenen Eigenlösungen stimmen mit überraschender Genauigkeit mit den gemessenen Energieniveaus von Atomen überein. Aber die Matrizen komplexerer Systeme wie des Urankerns werden zu „stachelig“, um sie zu „greifen“. Laut Dyson können solche Kernel daher mit einer Zufallsmatrix verglichen werden. Viele Wechselwirkungen innerhalb von Uran - Elemente einer unbekannten Matrix - sind so komplex, dass ihre Mischung wie viele überlagerte Geräusche Rauschen erzeugt. Infolgedessen verhält sich die unbekannte Matrix, die den Kernel steuert, wie eine Matrix mit Zufallszahlen, und ihr Spektrum ist universell.


Solche, nicht verbundenen Wermut, haben keine Universalität, ihr Spektrum ist zufällig

Wissenschaftler haben noch kein intuitives Verständnis dafür entwickelt, warum komplexe Systeme diese und keine andere zufällige / periodische Sequenz demonstrieren. "Das wissen wir nur aus den Berechnungen", sagt Wu. Ein weiteres Rätsel ist ihre Verbindung mit der Riemannschen Zeta-Funktion, in der sich Universalität im Spektrum der Nullen manifestiert. Diese Nullen hängen eng mit der Verteilung der Primzahlen zusammen - den irreduziblen ganzen Zahlen, aus denen der Rest besteht. Mathematiker haben lange nach einer Beschreibung der Verteilung von Primzahlen auf einer Zahlenlinie von 1 bis unendlich gesucht, und die Universalität gibt ihnen den Schlüssel. Einige glauben, dass eine Riemannsche Zeta-Funktion ausreichend komplex und kohärent sein kann, um Universalität zu besitzen. Die Entdeckung einer solchen Matrix hätte einen „starken Einfluss“ auf das Verständnis der Verteilung von Primzahlen, wie Paul Bourgade, ein Harvard-Mathematiker, sagte.

Es ist möglich, dass die Erklärung noch tiefer verborgen ist. "Es kann sich herausstellen, dass die Matrix der Universalität und Zeta-Funktion des Wigner keine Matrix ist, sondern eine mathematische Struktur, die noch nicht entdeckt wurde", sagt Erdös. "Wigner-Matrizen und Zeta-Funktionen können unterschiedliche Darstellungen dieser Struktur sein."

Viele Mathematiker suchen nach einer Antwort ohne Garantie. „Niemand hat sich vorgestellt, dass Busse in Cuernavac ein solches Beispiel sein würden. Niemand hätte gedacht, dass Nullen der Zeta-Funktion ein weiteres Beispiel wären, sagt Dyson. "Das Schöne an der Wissenschaft ist ihre Unvorhersehbarkeit, und alles, was nützlich ist, kommt von Überraschungen."

Source: https://habr.com/ru/post/de399535/