IT-Spezialisten gehen auf unbefestigten Straßen
Nach Jahrzehnten der Stagnation wurden neue Abkürzungen für das Problem der reisenden Verkäufer gefunden.
Vor nicht allzu langer Zeit hat ein Forscherteam von Stanford und der McGill University den 35-jährigen Rekord in der Informatik um einen unvorstellbar geringen Betrag gebrochen - um vier Hundertstel einer Billionstel Billionstel Billionstel Prozent. Der Durchbruch - ein Verkäuferproblem, das im Problem der Informatikklassiker gemacht wurde - war für jeden praktischen Wert zu klein, aber er hauchte neues Leben auf der Suche nach verbesserten Näherungslösungen.Die Aufgabe ist wie folgt aufgebaut: Für eine Reihe von Städten, die durch Straßen verbunden sind, muss der kürzeste Weg gefunden werden, um jede Stadt mit einer Rückkehr zum Ausgangspunkt zu besuchen. Die Lösungen für das Problem haben praktische Anwendungen, vom Bohren von Löchern in Leiterplatten über das Verwalten des Aufgabenplans auf einem Computer bis hin zum Organisieren der Eigenschaften des Genoms.Das Verkäuferproblem ist leicht zu formulieren und - theoretisch - leicht zu lösen, indem alle möglichen geschlossenen Pfade überprüft werden, um den kürzesten zu finden. Das Problem beim Brute-Force-Ansatz besteht darin, dass mit zunehmender Anzahl von Städten die entsprechende Anzahl von Pfaden sehr schnell die Fähigkeiten der schnellsten Computer übersteigt. Für zehn Städte gibt es mehr als 300.000 Routen. Für 15 Städte steigt ihre Zahl auf 87 Milliarden.Christofides-Algorithmus
In der frühen Computer-Ära hofften Mathematiker, dass jemand einen bequemen Ansatz für das Problem finden würde - einen Algorithmus, mit dem es in angemessener Zeit gelöst werden kann. Obwohl Programmierer in bestimmten Fällen Fortschritte erzielt haben - den kürzesten Weg für 49 Städte in den 1950er Jahren, für 2.392 Städte in den 1980er Jahren und für 85.900 Städte im Jahr 2006 -, schlug niemand einen Algorithmus vor, der das Problem im allgemeinen Fall effektiv löst. Nach der bemerkenswerten Arbeit von 1972 ist es möglich, dass ein solcher Algorithmus überhaupt nicht existiert. Der Informatiker Richard Karp von der University of California in Berkeley hat gezeigt, dass das Verkäuferproblem NP-vollständig ist, was bedeutet, dass es keinen effizienten Algorithmus gibt (es sei denn, jemand beweist, dass P = NP ist - aber die meisten Wissenschaftler glauben, dass dies nicht der Fall ist). .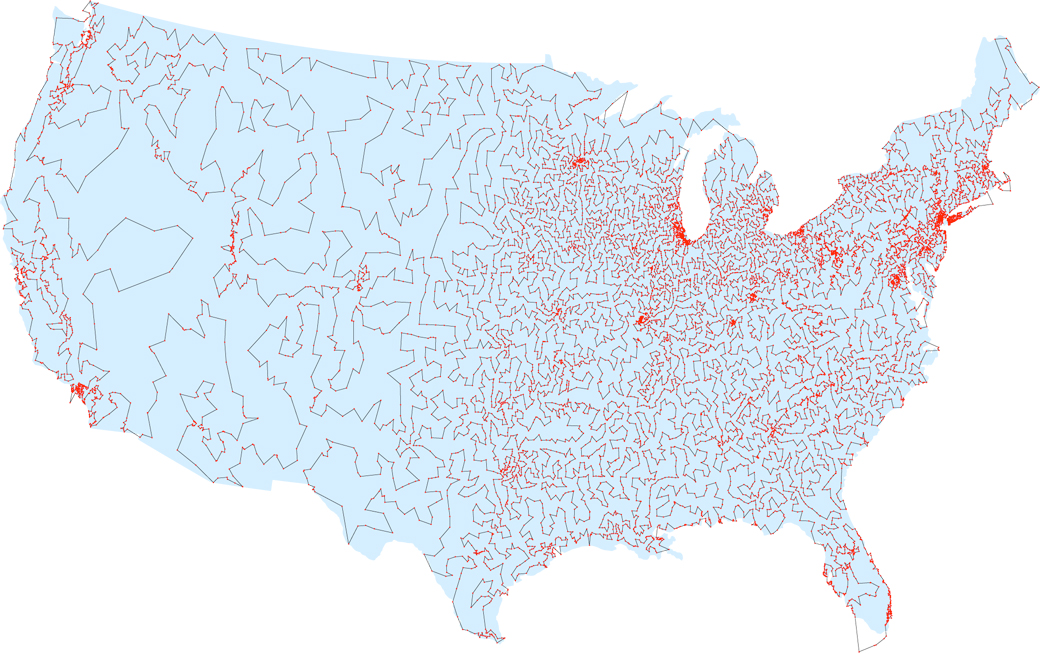
Der kürzeste Weg durch alle 13.509 Städte in den Vereinigten Staaten mit mehr als 500 Einwohnern (nach Angaben von 1998)Nach der Veröffentlichung von Karp begannen viele Informatiker mit der Entwicklung eines effektiven Algorithmus, um ungefähre Lösungen für das Problem zu finden - geschlossene Pfade, deren Länge nur geringfügig länger als die kürzeste ist. Und hier hatten sie mehr Glück - 1976 entwickelte Nikos Christofides, Professor am Imperial College London, einen Algorithmus, der Pfade erzeugt, die garantiert den kürzesten Pfad nicht um mehr als 50% überschreiten.Nach seiner Erstellung haben viele Wissenschaftler entschieden, dass dieser Algorithmus, der für die Schüler einfach genug ist, um in einer Stunde zu lernen, zu einer Zwischenverbindung wird, wonach eine komplexere, besser annähernde wahre Lösung gefunden wird. Aber Jahrzehnte später tauchten solche Algorithmen nie auf."Fast alle Informatikstudenten haben Wochen oder Monate damit verbracht, den Algorithmus von Christofides zu verbessern", sagte Sanjeev Arora, Wissenschaftler an der Princeton University.Schließlich ging das Team von Stanford und McGill im Jahr 2011 über die 50% -Garantie für bestimmte Arten von Verkäuferaufgaben hinaus und zeigte, dass ihre Lösungen den kürzesten Weg um nicht mehr als 49,99999999999999999999999999999999999999999999999996% überschreiten würden.Seitdem ist dank eines neuen Blicks auf das Problem eine Reihe verbesserter Näherungsalgorithmen erschienen. Obwohl diese Annäherungen nur für bestimmte Arten von Aufgaben als reisender Verkäufer gelten, ist ihr Ansatz laut Michael Gomans, IT-Spezialist am Massachusetts Institute of Technology, vielversprechend."Wir haben die Oberfläche nur leicht berührt", sagt er. "Ich glaube, dass wir in fünf Jahren vielleicht beeindruckendere Ergebnisse erzielen werden."Kürzester Baum
Mona Lisa als Pfad zwischen 100.000 StädtenDer Christofides-Algorithmus beginnt nicht mit der Suche nach dem kürzesten Pfad, sondern mit der Suche nach einem minimalen Spannbaum - einer Reihe von Zweigen, die Städte ohne geschlossene Schleifen verbinden. Im Gegensatz zum kürzesten Weg ist der minimale Spannbaum recht einfach zu erstellen. Sie müssen zunächst nach dem kürzesten Weg zwischen den beiden Städten suchen. Dies wird der erste Zweig sein. Um Folgendes hinzuzufügen, müssen Sie den kürzesten Weg zwischen der neuen Stadt und einer der beiden vorherigen finden - und so weiter, bis alle Städte abgedeckt sind.Der resultierende Baum ist keine der möglichen Lösungen für das Problem der reisenden Verkäufer, da er uns keinen geschlossenen Weg gibt. Aber es kann in einen solchen Pfad verwandelt werden, indem man sich vorstellt, dass die Zweige Wände sind, und dann am Baum entlang geht, so dass Ihr Finger die Wand berührt, bis Sie zum Anfang kommen. Der resultierende Weg führt durch jede Stadt und kehrt zurück, ist aber normalerweise weit vom kürzesten Weg entfernt, da er viele Male entlang derselben Segmente verläuft - wir gehen jede Wand in einem Baum zweimal, einmal auf jeder Seite.Der resultierende Pfad ist jedoch im schlimmsten Fall nicht länger als der kürzeste Pfad zweimal. Durch Hinzufügen speziell ausgewählter Zweige und Anwendung einiger Tricks zeigte Christofides, wie dieser Pfad so geschnitten werden kann, dass er den kürzesten nicht um mehr als 50% überschreitet.Ein minimaler Spanning Tree ist ein natürlicher Ausgangspunkt für die Erstellung einer kurzen Problemumgehung. Dieser Ansatz diente aber auch als Ausgangspunkt für Forscher, die versuchten, eine 50% ige Christofides-Garantie zu erhalten. Obwohl ein minimaler Spannbaum zunächst effektiv aussieht, sind andere Bäume möglicherweise besser für die Konvertierung von Bäumen in eine Problemumgehung geeignet. Sie müssen beispielsweise einem Baum ohne Zweige nur einen Pfadabschnitt hinzufügen, damit er zu einer Problemumgehung wird.Ziel war es also, einen Baum zu finden, der ein Gleichgewicht zwischen Länge und einfacher Konvertierung in eine Problemumgehung herstellt. Es gibt keine effektiven Algorithmen für die Suche nach einem idealen Baum (wenn P = NP nicht wahr ist), aber ein erfolgreicher Näherungsalgorithmus muss nur gut genug finden.Bruchreise
Der Weg zu einem "einigermaßen guten" Baum beinhaltete eine beliebte, wenn auch nicht intuitive Technik, die fraktionierte Lösungen für bestimmte Aufgaben erkannte. Zum Beispiel kann eine fraktionierte Problemumgehung das Reisen auf halbem Weg zwischen Minneapolis und Detroit und auf halbem Weg zwischen Cleveland und Detroit umfassen. Aus praktischer Sicht ist ein solcher Weg nicht sinnvoll. Aber es kann mathematisch genau beschrieben werden und im Gegensatz zum klassischen Problem des Handlungsreisenden kann eine solche gebrochene Version effizient gelöst werden.Viele Approximationsprobleme in der Informatik können gelöst werden, indem Lösungen für die gebrochene Version des Problems berechnet und dann die Anteile intelligent gerundet werden, um eine ungefähre Lösung für das ursprüngliche Problem zu erhalten. Bis vor kurzem hatte jedoch noch niemand herausgefunden, wie dies im Fall des Problems der reisenden Verkäufer zu tun ist.Im Jahr 2009 entwickelten Amin Saberi von der Stanford University und der damalige Doktorand Arash Asadpour ein allgemeines Rundungsschema, bei dem anhand von Zufallszahlen eine ganzzahlige Lösung ausgewählt wird, bei der so viele Eigenschaften der fraktionierten Lösung wie möglich erhalten bleiben. Saberi glaubte, dass dieses Muster an einen "schweren Hammer auf der Suche nach einem Nagel" erinnerte. Und er vermutete, dass die Aufgabe des Verkäufers der richtige Nagel sein könnte.Einige Monate später zeigten Sabre, Asadpur, Gomans, der Stanford-Doktorand Shayan Gharan und Aleksander Madry, die jetzt an der Federal Polytechnic School in Lausanne in der Schweiz arbeiten, dass die neue Rundungstechnik einen guten Näherungsalgorithmus für eine der Optionen liefern kann Aufgaben des Verkäufers, der "asymmetrische" Fall. Ein Jahr später verwendeten Sabre, Garan und Mohit Singh von der McGill University denselben Ansatz, um einen neuen Näherungsalgorithmus für das normale Problem der reisenden Verkäufer zu entwickeln.
Das größte Problem für reisende Verkäufer war der Weg zwischen 85.900 Städten, der 2006 berechnet wurde. Der Standort der „Städte“ entspricht dem Design eines bestimmten Computerchips, der im Labor von Bell erstellt wurde, und die Lösung ist der kürzeste Weg für das LaserschneidenNachdem der neue Algorithmus eine Karte mit Städten und Routen erhalten hat, berechnet er zunächst die genaue Bruchlösung des Problems der reisenden Verkäufer. Anschließend rundet er diese Lösung auf einen Spanning Tree ab, der theoretisch einem Gleichgewicht zwischen Länge und einfacher Konvertierung in eine Problemumgehung nahe kommen sollte. Schließlich enthält der Algorithmus diesen Baum - und nicht den minimalen Spannbaum - im Christofides-Netzwerk.Der neue Algorithmus war „eine Idee, die wir in ein paar Stunden erklären konnten, aber der Beweis dauerte ungefähr ein Jahr“, sagt Saberi.Nach einer langen Analyse konnte das Stanford / McGill-Team den Christofides-Algorithmus für eine breite Unterklasse von Verkäuferaufgaben, „Grafik“, um einen kleinen Bruchteil verbessern. Einige Monate später verwendeten andere vom Erfolg inspirierte Teams andere Rundungsschemata, um Algorithmen für den grafischen Fall mit besseren Annäherungen zu erhalten. Der aktuelle Rekord liegt bei 40%, was viel besser ist als 50% von Christofides.Der grafische Fall „enthält viele der gleichen Schwierigkeiten, die beim allgemeinen Problem auftreten“, sagt Arora und fügt hinzu, dass die im grafischen Fall arbeitenden Schemata auch für das allgemeine Problem des Handlungsreisenden nützlich sein können.Dennoch, sagt Sabre, erfordert die Lösung des allgemeinen Problems der ungefähren Verkäufer wahrscheinlich neue Ideen. „Eine mathematische Entdeckung ist wie eine Bewegung in einem dunklen Raum. Sie greifen nach einem Stuhl, greifen nach einem Tisch und umschreiben ihn “, umschreibt er den Mathematiker Andrew Wiles. „Irgendwann findet die Hand einen Schalter und plötzlich wird alles klar. Bei der Aufgabe des Verkäufers scheint es mir auch nach so vielen Arbeiten, die so viele Grenzen des Möglichen gefunden haben, nicht, dass wir diesen Schalter bereits gefunden haben. “Source: https://habr.com/ru/post/de399873/
All Articles