(Fortsetzung. Vorheriger Teil: „Automatisierung aus DNA und Proteinen: Was hat sie mit Elektronik gemeinsam?“ )Wir haben uns auf die Tatsache festgelegt, dass das Laktoseoperon dem logischen UND-Element ähnlich ist. Aber woher kommen seine digitalen Eigenschaften? Schließlich sind beide Eingangssignale (cAMP- und Lactose-Konzentrationen) tatsächlich analog. Versuchen wir, die Eingabefunktionen des Laktoseoperons zu zeichnen.Jeder Eingang des Laktoserepressors besteht aus zwei Stufen der molekularen Erkennung. Laktose bindet an den Laktoserepressor und der Repressor bindet an DNA. Es gibt mehrere zehn Repressormoleküle in der Zelle, von denen jedes, solange keine Laktose vorhanden ist, an den Beginn des Laktoseoperons binden kann. Wenn es dort gebunden ist, kann die RNA-Polymerase nicht mit der Arbeit beginnen. Aufgrund der thermischen Bewegung des Repressormoleküls fällt es immer wieder von der DNA ab und bindet sich zurück. Wenn es überhaupt keinen Repressor gibt, arbeitet das Operon mit voller Leistung (der Einfachheit halber denken wir jetzt, dass es einen Überschuss an katabolischem Aktivator gibt). Bei niedrigen Konzentrationen des Repressors reduziert es die Aktivität des Operons nahezu linear. Aber dann ist die Wirkung jedes neuen Teils des Repressors immer geringer, und im Allgemeinen liegt der Abhängigkeitsgraph nahe an der Übertreibung y = 1 / (x + 1)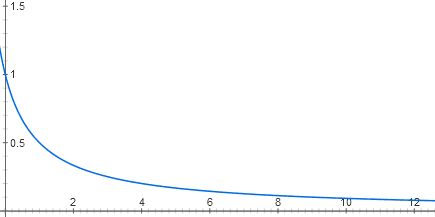
Matan. . ?
, , . , :
A + B <-> C
, , - . , - ( , [A], [B] [C] ). : , , .
[C] / ([A] * [B]) = K
. (. . ) . , , .
, , , , ( ) . [C] ([A] * [B]) .
, : RepA + OpA <-> Op ( ). {R-O} = [Op] / ([OpA] * [RepA]). [] ( ) [RepA] ( ). , , : [Op] + [OpA] = 1
[Op] [OpA] :
{R-O} = (1 — [OpA]) / ([OpA] * [RepA])
:
[OpA] = 1 / (K{R-O} * [RepA] + 1)
y = 1 / (x + 1)
Repressormoleküle schweben in der Zelle und binden nur in Viererpackungen an DNA. Damit die aktive Form des Repressors inaktiv wird, muss er an vier Laktosemoleküle binden - ein oder zwei reichen nicht aus, Sie benötigen ein Laktosemolekül für jede Proteinuntereinheit des Quad-Repressors. Während die Zelle wenig Laktose enthält, binden ihre Moleküle an den Repressor eins oder zwei und sie bleibt aktiv. Nach einer bestimmten Schwellenkonzentration von Laktose bindet die Mehrheit der Repressormoleküle vier Laktosemoleküle und geht in eine inaktive Form über. Der Graph der Repressoraktivität in Abhängigkeit von der Laktosemenge hat daher eine S-Form und wird durch eine Funktion der Form y = 1 / (1 + x ^ 4) beschrieben.Matan[RepA] [Lac]. , : .
RepA + 4 Lac <-> Rep
:
{R-L} = [Rep] / ([RepA] * [Lac]^4)
, :
[Rep] + [RepA] = n, n ≈ 50
, [RepA] = n / ({R-L} * [Lac]^4 + 1)
Um nun die Eingangscharakteristik des Operons für Laktose zu erhalten, ist es notwendig, die zweite Funktion durch die erste zu ersetzen. Es hat die Form bis zu den Koeffizienteny = 1 / (1 + (1 / (1 + x ^ 4)))Ihr Zeitplan ist auch S-förmig. Es stellt sich heraus, dass das Laktoseoperon nicht auf niedrige Laktosekonzentrationen reagiert. Wenn die Schwellenkonzentration erreicht ist, erscheinen inaktive Repressormoleküle, die jeweils vier Laktosen binden, und das Operon schaltet sich ziemlich scharf ein.Der zweite regulatorische Input des Lactose-Operons besteht ebenfalls aus zwei Schritten der molekularen Erkennung: cAMP bindet an den Aktivator und der Aktivator an DNA. Der Unterschied zum Lactoseeinlass besteht darin, dass hier die Bindung von Molekülen (Aktivator oder cAMP) die Aktivität dessen erhöht, was sie kontaktiert haben (Operon oder Aktivator). Das heißt, die Diagramme gehen von Null und nähern sich der horizontalen Linie irgendwo über der X-Achse.Matan, , :
2 + Akt <-> AktA
K{-} = [AktA] / ([Akt] * []^2)
, [AktA] [Akt] , 100 , . [Akt] [AktA], :
K{-} = [AktA] / ((100 — [AktA]) * []^2)
[AktA] = K{-} * []^2 / (1 + K{-} * []^2)
[AktA] [] y = x^2 / (1 + x^2)
Aufgrund der Bindung von zwei cAMP-Molekülen sieht der Graph nicht wie eine Übertreibung aus, sondern wie eine S-förmige Kurve. Der Schwelleneffekt ist zwar weniger auffällig als in der Grafik für Laktose, da der Grad nicht der vierte, sondern nur der zweite ist.Die Abhängigkeit der Operonaktivität von der Menge des Aktivators hat eine andere Nuance. Wenn die Bindung des Repressors das Operon fast vollständig unterdrückt (irgendwo bis zu 0,1%, was niedriger als der biochemische Messfehler ist), unterdrückt das Fehlen eines Aktivators die Aktivität nur bis zu 5%. Daher wird das Diagramm nicht von Null, sondern vom Punkt (0; 0,05) ausgegeben:y = 0,05 + (0,95 * x / (1 + x))Matan« , » ,
= [OpA] + 0,05 * [Op]
[OpA] [AktA] . , , [AktA] . , , [AktA] , :
[OpA] = K{-O} * [AktA] / (K{-O} * [AktA] + 1)
y = x / (1 + x)
, ! , (1 — ) * 0,05. , , :
y = 0,05 + (0,95 * x / (1 + x))
Es bleibt die Abhängigkeit der Operonaktivität von der Konzentration von cAMP zu erhalten. Ersetzen Sie dazu die erste Formel (für die Konzentration der aktiven CAP in Abhängigkeit von der Konzentration der cAMP) in der zweiten Formel (für die Aktivität des Operons aus der Konzentration der aktiven ATS) ...... und erhalten Sie eine vierstöckige Fraktion:Wir haben die komplexeste Funktion von allen in diesem Artikel. Sein Graph sieht jedoch aus wie ein Graph einer einfacheren Abhängigkeit der aktiven CAP von der cAMP-Konzentration, y = x ^ 2 / (1 + x ^ 2):Es ist auch eine S-förmige Kurve mit einem gewissen Schwelleneffekt, die sich langsam der Horizontalen y = 1 nähert. Sie beginnt nur nicht bei Null, sondern beim Punkt (0; 0,05).Es bleibt zu verstehen, wie die beiden Eingänge interagieren. Im Fall des Laktoseoperons ist die Antwort einfach - überhaupt nichts. Laktoserepressor und katabolischer Aktivator beeinflussen die gegenseitige Bindung an DNA nicht. Daher kann die Bindung dieser beiden Proteine als unabhängige Ereignisse angesehen werden. Die volle Aktivität des Operons wird erreicht, wenn sowohl der Aktivator als auch der Repressor nicht angeschlossen sind. Die Wahrscheinlichkeit eines solchen Zusammentreffens ist gleich dem Produkt der Wahrscheinlichkeiten von jedem von ihnen getrennt. Um die Aktivitätsfunktion des Lactose-Operons aus zwei Variablen ([Lac]) und ([cAMP]) zu erhalten, müssen Sie nur die Funktionen jeder dieser Variablen multiplizieren:Aktivität = (1 / (1 + (1 / (1 + [Lac] ^ 4))) (0,05 + 0,095 * ([cAMP] ^ 2 / (1 + [cAMP] ^ 2)) / ( 1 + ([cAMP] ^ 2 / (1 + [cAMP] ^ 2))))Dreidimensionaler Graph dieser FunktionEs sieht aus wie ein Plateau, das auf zwei Seiten in Schluchten endet. Die rechte Schlucht (niedrige Laktosekonzentrationen) ist tiefer und flacher als die linke (niedrige cAMP-Konzentrationen).Im wirklichen Leben gibt es in E. coli entweder überhaupt keine Laktose (meistens) oder seine Konzentration ist höher als der Schwellenwert, und der Laktoserepressor stört praktisch nicht den Betrieb des Operons (wenn der Besitzer etwas Milch gegessen hat). Die Konzentration von cAMP ist ein internes Signal, das von der Zelle selbst erzeugt wird. Es ist entweder zu klein, um das Laktoseoperon aufzunehmen (wenn Glukose oder Stärke vorhanden sind), oder es ist ausreichend, um 95% oder mehr einzuschalten (wenn nichts schmackhafter als Laktose ist). Das heißt, fast immer befindet sich das Laktoseoperon entweder unter den Bedingungen eines Plateaus in diesem Diagramm oder in einer der Schluchten.Die Eingabefunktionen des Lactose-Operons werden experimentell gemessen. Die Messmethode ähnelt der Technik des Debuggens von Mikrocontrollern, "die LED am Ausgangszweig hängen". Die regulatorische Region des Operons wird genommen und mit dem grün fluoreszierenden Proteingen verknüpft. Dieses Genkonstrukt wird in die Zellen von Escherichia coli inseriert, aus denen das reguläre Lactoseoperon entfernt wird (so dass die Lactosekonzentration vom Experimentator streng festgelegt wird) und in das Standardsystem, das Hunger mit cAMP-Spiegeln codiert. Danach kann die Aktivität des Lactoseoperons mit einem Spektrophotometer entsprechend dem Grad der grünen Fluoreszenz genau gemessen werden. Es stellt sich heraus, dass die Theorie innerhalb der Grenzen der Messgenauigkeit (1%) vollständig mit dem Experiment konvergiert .Der Boden der linken Schlucht im Diagramm der Eingabefunktion (bei niedrigen Konzentrationen von cAMP) liegt über Null. Dies ist kein Fehler, sondern ein Merkmal: Dank dessen ist E. coli in Gegenwart mehrerer Zucker gleichzeitig bereit, schnell auf Laktose umzusteigen, wenn die Glukose vorbei ist. Escherichia coli-Mutanten, bei denen die regulatorische Funktion des Lactose-Operons näher am reinen AND liegt (dh das Operon funktioniert nicht ohne cAMP), wechseln für eine Stunde oder länger von Glucose zu Lactose: Zum Zeitpunkt der Glucose-Erschöpfung haben sie keine Lactose-Aufnahmeenzyme, was bedeutet, dass es keine gibt Energie, um sie schnell zu machen. Normaler Escherichia coli ("Wildtyp") erfüllt diesen Punkt, hat bereits einige Laktose-Assimilationsenzyme und es dauert 15 bis 20 Minuten, bis er vollständig auf neuen Zucker umgestellt ist.Lassen Sie uns nun vom Laktoseoperon abschweifen und genauer untersuchen, wozu die logischen Elemente auf einer solchen chemischen Basis in der Lage sind. Fast überall in biochemischen Signalsystemen finden wir molekulare Erkennung, die durch Funktionen der Form y = x ^ n / (1 + x ^ n) für Aktivatoren und y = 1 / (1 + x ^ n) für Repressoren beschrieben wird. Der Grad n in diesen Funktionen zeigt die Anzahl der Moleküle des gleichen Typs, die gebunden werden müssen, um einen Effekt zu erzielen, und ist normalerweise gleich 1, 2 oder 4 (meistens 2). Komplexere logische Schlüssel können erhalten werden, indem am Anfang des Operons mehr regulatorische Proteinbindungsstellen hinzugefügt werden. Es kann mehr als zwei Arten dieser Proteine geben. Die Auswirkungen verschiedener Proteine auf die Landung von RNA-Polymerase können sich addieren (OR) oder multiplizieren (AND).Im Allgemeinen werden wir uns jedoch mit einer Kombination (Addition oder Multiplikation) der Grundfunktionen y = x ^ n / (1 + x ^ n) und y = 1 / (1 + x ^ n) mit unterschiedlichen Graden und Koeffizienten befassen.Einige interessante Funktionen sind sehr einfach. Beispielsweise kann dasselbe regulatorische Protein (in gepaarter Form) an zwei Regionen des Promotors binden. In einem Abschnitt wirkt es als Repressor und in einem anderen als Aktivator. Damit das Operon funktioniert, muss die Repressor-Site leer und die Activator-Site ausgelastet sein. Es stellt sich eine Funktion mit einem klaren Maximum heraus:y = (1 / (1 + x ^ 2)) * (x ^ 2 / (1 + x ^ 2))Ohne dieses Protein ist das Operon inaktiv, weil die Aktivatorstelle leer ist, und in hohen Konzentrationen ist es inaktiv, weil die Stelle beschäftigt ist Repressor. Die maximale Aktivität liegt vor, wenn sowohl die Stelle des Aktivators als auch die Stelle des Repressors mit einer Wahrscheinlichkeit von 50% belegt sind.Sie können immer noch zwei Aktivatorbindungsstellen herstellen, von denen eine den Aktivator stark an DNA bindet, das Gen jedoch schwach aktiviert, die andere schwach an DNA bindet, das Gen jedoch stark aktiviert. In diesem Fall erhalten wir eine Funktion wie y = x ^ 4 / (1 + x ^ 4) + 0,3 * (10x) ^ 4 / (1 + (10x) ^ 4) mit einem schrittweisen Diagramm:Mathe, ja! Können Sie in den Kommentaren sagen, was sonst noch möglich ist und was nicht durch Addition und Multiplikation dieser Grundfunktionen y = x ^ n / (1 + x ^ n) und y = 1 / (1 + x ^ n) erhalten werden kann?Im nächsten Teil werden wir uns mit Schaltkreisen solcher logischen Elemente befassen.