Ich werde nicht lügen, ich freue mich sehr auf den Film Spider-Man: Homecoming [Spider-Man: Homecoming]. In der Zwischenzeit wird die einzige Möglichkeit für mich darin bestehen, die Physik von Spider-Man zu betreiben. Und ich werde mich um seine neuen Spinnennetzflügel kümmern, die im letzten Trailer zu sehen sind.Für Fans stelle ich fest, dass einige der Original-Comics über Spider-Man wirklich zeigten, wie er sie benutzt, obwohl er sie nicht immer zum Fliegen benutzte.Physikplanung
Was passiert, nachdem Spider-Man aus einem Gebäude gesprungen ist? Ich kann seine Bewegung simulieren, indem ich akzeptiere, dass drei Kräfte auf ihn wirken - Schwerkraft, Luftwiderstand und Auftrieb. Mit Ihrer Erlaubnis werde ich jeden von ihnen beschreiben.• Schwerkraft - eine konstante Abwärtskraft proportional zur Masse des Notfalls (zumindest auf der Erdoberfläche).• Widerstand. Stellen Sie sich vor, Sie ziehen ein Objekt durch ein riesiges Meer von Tischtennisbällen. Ersetzen Sie die Kugeln durch Luft - und es wird ungefähr gleich sein. Der Widerstand nimmt mit der Geschwindigkeit zu.• Hebekraft. Stellen Sie sich wieder Kollisionen mit Bällen vor, aber solche, nach denen die Bälle abprallen. Wenn Sie die Bälle durch Luft ersetzen, erhalten Sie je nach Anstellwinkel, Oberfläche und Geschwindigkeit einen Auftrieb.Hier ist ein schönes Diagramm der Kräfte einer Person, die auf den Flügeln eines Notfalls plant. Ja, während wir es mit einem Dreieck modellieren.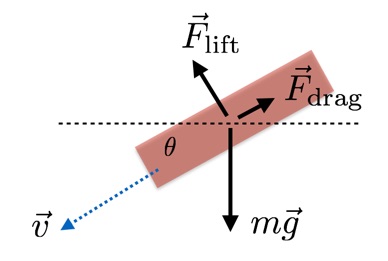 In unserem einfachen Modell ist die Hubkraft senkrecht zur Geschwindigkeit und der Widerstand ist in die entgegengesetzte Richtung gerichtet. Um die Bewegung eines Notfalls mit Flügeln zu simulieren, benötige ich für beide eine Formel.
In unserem einfachen Modell ist die Hubkraft senkrecht zur Geschwindigkeit und der Widerstand ist in die entgegengesetzte Richtung gerichtet. Um die Bewegung eines Notfalls mit Flügeln zu simulieren, benötige ich für beide eine Formel.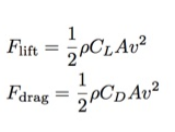 Dies sind Werte von Kräften, die für uns wichtig sind. Sie sind ähnlich, mit Ausnahme von C L (Auftriebskoeffizient) und C D (Widerstandskoeffizient). In beiden Fällen ist ρ die Luftdichte (1,2 kg / m 3 ) und v ist die Geschwindigkeit.Was ist A? Dies ist die Querschnittsfläche einer Person (in unserem Fall Notfall). Theoretisch sollte sich A für Widerstand und Hubkraft je nach Anstellwinkel unterscheiden. Aber ich weiß nicht immer genau, was ich tue - deshalb habe ich mit verschiedenen Quellen und dem Artikel von 2011 „ Die Flugbahn eines fallenden Batman"aus dem physischen Journal Journal of Physics Special Topics. Darin verwendeten die Autoren den gleichen Bereich für Widerstand und Auftrieb, also werde ich das gleiche tun.
Dies sind Werte von Kräften, die für uns wichtig sind. Sie sind ähnlich, mit Ausnahme von C L (Auftriebskoeffizient) und C D (Widerstandskoeffizient). In beiden Fällen ist ρ die Luftdichte (1,2 kg / m 3 ) und v ist die Geschwindigkeit.Was ist A? Dies ist die Querschnittsfläche einer Person (in unserem Fall Notfall). Theoretisch sollte sich A für Widerstand und Hubkraft je nach Anstellwinkel unterscheiden. Aber ich weiß nicht immer genau, was ich tue - deshalb habe ich mit verschiedenen Quellen und dem Artikel von 2011 „ Die Flugbahn eines fallenden Batman"aus dem physischen Journal Journal of Physics Special Topics. Darin verwendeten die Autoren den gleichen Bereich für Widerstand und Auftrieb, also werde ich das gleiche tun.Modellierung der Flugbahn
Wenn ein Notfall von einem Gebäude springt, wie weit kann er sich bei einem Sturz bewegen? Welchen Unterschied geben ihm Spinnenflügel? Die Modellierung des Ausnahmezustands ist nicht so einfach, da Widerstand und Auftrieb von der Geschwindigkeit abhängen. Eine solche Flugbahn kann nur mit einem numerischen Modell berechnet werden, bei dem die Bewegung in kleine Schritte unterteilt ist.Machen wir die Annäherung. Zunächst berechnen wir die Oberfläche des Notfalls. Grob geschätzt habe ich: Was gibt uns eine Fläche von ca. 0,651 m 2 mit Flügeln und 0,513 m 2 ohne Flügel . Andere Werte:• Hebekoeffizient = 1,45 (Wert aus Batmans Arbeit)• Widerstandskoeffizient = 0,4 (vom selben Ort)• Gewicht = 64 kg• Anfangsgeschwindigkeit = 8 m / s (horizontal)• Und noch eine Annahme: ein konstanter Anstellwinkel, in dessen Zusammenhang sich die Widerstands- und Auftriebskoeffizienten nicht ändern.Ohne zu zögern sprang ich in die Welt der numerischen Modelle. Ich habe Kommentare im Code hinterlassen, damit Sie ihn für die Hausaufgaben neu erstellen können.
Was gibt uns eine Fläche von ca. 0,651 m 2 mit Flügeln und 0,513 m 2 ohne Flügel . Andere Werte:• Hebekoeffizient = 1,45 (Wert aus Batmans Arbeit)• Widerstandskoeffizient = 0,4 (vom selben Ort)• Gewicht = 64 kg• Anfangsgeschwindigkeit = 8 m / s (horizontal)• Und noch eine Annahme: ein konstanter Anstellwinkel, in dessen Zusammenhang sich die Widerstands- und Auftriebskoeffizienten nicht ändern.Ohne zu zögern sprang ich in die Welt der numerischen Modelle. Ich habe Kommentare im Code hinterlassen, damit Sie ihn für die Hausaufgaben neu erstellen können.GlowScript 2.1 VPython
A1=0.651
A2=0.513
g=vector(0,-9.8,0)
m=64
CL=1.45
CD=0.4
rho=1.2
v0=8
p=vector(v0,0,0)*m
p2=p
t=0
dt=0.01
h=40
r=vector(0,h,0)
r2=r
f1=series(color=color.red)
f2=series(color=color.blue)
while r.y>0:
v=p/m
v2=p2/m
Fd=-.5*rho*A1*CD*(mag(v)**2)*norm(v)
Fd2=-.5*rho*A2*CD*(mag(v2)**2)*norm(v2)
FL=-.5*rho*A1*CL*(mag(v)**2)*cross(norm(v),vector(0,0,1))
FL2=-.5*rho*A2*CL*(mag(v2)**2)*cross(norm(v2),vector(0,0,1))
F=m*g+Fd+FL
F2=m*g+Fd2+FL2
p=p+F*dt
p2=p2+F2*dt
r=r+p*dt/m
r2=r2+p2*dt/m
t=t+dt
f1.plot(r.x,r.y)
f2.plot(r2.x,r2.y)
print("Glide Ratio 1 = ",-p.x/p.y)
print("Glide Ratio 2 = ", -p2.x/p2.y)
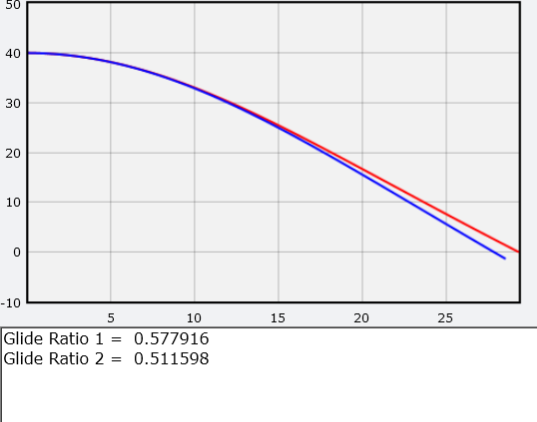 In meinem Modell repräsentiert die rote Linie die Flugbahn des Notfalls mit Flügeln und die blaue Linie ohne Flügel. Ich leite auch den Wert der aerodynamischen Qualität ab. Da es sich am Ende mit einer konstanten Geschwindigkeit bewegt, ist dieses Verhältnis einfach gleich dem Verhältnis der x-Komponente des Impulses geteilt durch die y-Komponente.HausaufgabenVerwenden Sie dieses numerische Modell , um die folgenden Fragen zu beantworten . Mach dir keine Sorgen, du wirst nichts kaputt machen. Wenn Sie etwas mit dem Code tun, starten Sie ihn einfach neu und beginnen Sie von vorne.• Laut WikipediaFür einen Fallschirmspringer, der in einem geflügelten Anzug springt, hat die aerodynamische Qualität (das Verhältnis von Auftrieb zu Luftwiderstand) einen Wert in der Größenordnung von 2,5: 1 (dh unser Programm würde die Zahl 2,5 ableiten). Können Sie den Code korrigieren, damit das Programm einen solchen Wert erzeugt? Hinweis: Ändern Sie sowohl die Oberfläche als auch die Anfangsgeschwindigkeit.• Was ist, wenn ein Notfall senkrecht nach unten fällt? Welche Höchstgeschwindigkeit wird es mit Flügeln und ohne sie gewinnen?• Wie schnell muss sich der Notfall horizontal bewegen, damit er zu Beginn des Fluges eher nach oben als nach unten fliegt?• Kann ein Notfall nach unten springen, um schneller zu werden und für einige Zeit in den Horizontalflug zu gehen?• Können Sie ein verbessertes Modell erstellen, das den Anstellwinkel berücksichtigt? Vielleicht können Sie das, aber es scheint mir, dass das Fliegen mit niedriger Geschwindigkeit ein ziemlich kompliziertes Thema ist.
In meinem Modell repräsentiert die rote Linie die Flugbahn des Notfalls mit Flügeln und die blaue Linie ohne Flügel. Ich leite auch den Wert der aerodynamischen Qualität ab. Da es sich am Ende mit einer konstanten Geschwindigkeit bewegt, ist dieses Verhältnis einfach gleich dem Verhältnis der x-Komponente des Impulses geteilt durch die y-Komponente.HausaufgabenVerwenden Sie dieses numerische Modell , um die folgenden Fragen zu beantworten . Mach dir keine Sorgen, du wirst nichts kaputt machen. Wenn Sie etwas mit dem Code tun, starten Sie ihn einfach neu und beginnen Sie von vorne.• Laut WikipediaFür einen Fallschirmspringer, der in einem geflügelten Anzug springt, hat die aerodynamische Qualität (das Verhältnis von Auftrieb zu Luftwiderstand) einen Wert in der Größenordnung von 2,5: 1 (dh unser Programm würde die Zahl 2,5 ableiten). Können Sie den Code korrigieren, damit das Programm einen solchen Wert erzeugt? Hinweis: Ändern Sie sowohl die Oberfläche als auch die Anfangsgeschwindigkeit.• Was ist, wenn ein Notfall senkrecht nach unten fällt? Welche Höchstgeschwindigkeit wird es mit Flügeln und ohne sie gewinnen?• Wie schnell muss sich der Notfall horizontal bewegen, damit er zu Beginn des Fluges eher nach oben als nach unten fliegt?• Kann ein Notfall nach unten springen, um schneller zu werden und für einige Zeit in den Horizontalflug zu gehen?• Können Sie ein verbessertes Modell erstellen, das den Anstellwinkel berücksichtigt? Vielleicht können Sie das, aber es scheint mir, dass das Fliegen mit niedriger Geschwindigkeit ein ziemlich kompliziertes Thema ist.