Wenn wir zur Geschichte des Studierens von Flugwegen von der Erde zum Mond zurückkehren, dann müssen Sie vor eineinhalb Jahrhunderten zurückgehen, 1865, als Jules Vernes neuer Roman "Von der Erde zum Mond auf direkte Weise in 97 Stunden 20 Minuten" veröffentlicht wurde. Natürlich war dies weit entfernt von dem ersten Buch, das einen solchen Flug beschrieb, aber es war der erste Roman, in dem der Autor beschloss, die Beschreibung des Reisens aus wissenschaftlicher Sicht zu betrachten.Darüber hinaus ist der Grad der Vorbereitung dieses Textes jetzt besonders gut bekannt, da zum ersten Mal nicht nur die Raumfahrt gezeigt wurde, sondern alle manchmal sehr kleinen Nuancen detailliert analysiert wurden. Jetzt kritisieren sie den Roman gern für die Fehler, die der Autor gemacht hat. Bei einem solchen Arbeitsvolumen wäre es jedoch überraschend, wenn es überhaupt keine Fehler gäbe! Und jetzt sind es nicht seine Fehler, die ihn mehr in Erstaunen versetzen, sondern was er recht hatte. Zum Beispiel ist die Idee von Sauerstoffreinigungssystemen sowohl auf der Columbiada-Hülle als auch auf dem Sojus-Raumschiff sehr ähnlich. Nur Jules Verne hatte Natriumhydroxid, und jetzt wird Lithiumhydroxid verwendet.
Noch interessanter sind die Momente, in denen er trotz falscher Annahmen Recht hatte. Zum Beispiel kritisierte Perelman ihn dafür, dass er fehlerhafte Daten zur Flugzeit von der Erde zum Mond gegeben hatte, und machte sie sogar im Namen des Romans. Der Mathematiker führte genauere Berechnungen nach der angegebenen Methode durch, nachdem er eine Zahl in der Größenordnung von sechs Tagen erhalten hatte, zwei Tage mehr als im Roman. Und seine Berechnungen im Rahmen dieser Methode waren in der Tat richtig. Es ist wirklich möglich, nur in vier Tagen zum Mond zu fliegen (tatsächlich erreichten viele Geräte in ungefähr dieser Zeit den Mond), aber in sechs Tagen ist dies bereits unmöglich. Die Berechnungsmethode wurde vom Science-Fiction-Autor falsch gewählt, und die Zahl stellte sich als richtig heraus!Noch zum Beispiel, kurz nach der Veröffentlichung des Romans „Rund um den Mond“, bezweifelten viele die Möglichkeit einer solchen Flugbahn eines engen Vorbeiflugs des Mondes unter dem Einfluss nur von Gravitationskräften. Erst zu Beginn des 20. Jahrhunderts, als Umlaufbahnen in binären Sternensystemen bewertet wurden, wurde die Möglichkeit der Existenz solcher Umlaufbahnen wirklich gezeigt. Folgendes schrieb die englische Zeitschrift „Knowledge“ zu Beginn des 20. Jahrhunderts im Artikel „Astronomy by Jules Verne“:«, . , . . , . , , . , , , . . . . , . , , , ».Mit anderen Worten, die Aufgaben, die Jules Verne zu dieser Zeit zu lösen versuchte, standen nicht nur im Vordergrund der Wissenschaft - sie stellten oft Fragen, die die Wissenschaft dann nicht beantworten konnte.Man darf jedoch nicht vergessen, dass er das alles nicht alleine gemacht hat. Beim Schreiben aller seiner Bücher versuchte der Autor, sich an Spezialisten auf jedem Gebiet zu wenden. Nach seinen Tagebüchern wurden die Berechnungen für den Flug von der Erde zum Mond von seinem Cousin Henri Garce (1815-1871) durchgeführt, einem Mathematiklehrer am Lyceum von Napoleon (heute Lyceum von Heinrich IV.). Übrigens können Sie hier sein Buch in französischer Sprache sehen, das der Kosmographie der Leçons nouvelles de Cosmographie (1854) gewidmet ist. Und seine Berechnungen waren ziemlich genau. Zum Beispiel habe ich hier gemäß den Daten im Buch das genaue Startdatum für die Besatzung von Columbiada berechnet.
Henri Garcet (1815–1871)Wir hätten jedoch wahrscheinlich nichts über seine Berechnungen gewusst, wenn Jules Verne sie nicht ganz am Anfang des Buches „Rund um den Mond“ platziert hätte und sie im Gespräch mit der Besatzung der Columbiada-Granate verwendet hätte. Sie schreiben, dass die Leser der Zeitung "Debates" vom 7. November 1869 buchstäblich erstaunt waren, komplexe mathematische Berechnungen zu sehen - die Veröffentlichung des Romans begann in dieser Zeitung.So wurde das mathematische Modell des Fluges durch die Lippen von Michel Ardan und Barbicane beschrieben:„Weißt du, Barbicane, woran habe ich die ganze Nacht gedacht?“
- Worüber? Der Vorsitzende fragte.
— . , , , . : , , , .
— , — , — , , , , , .
— , , — .- - ?
— .
— ?
…
"Ja, lieber Freund." Nachdem ich alle bekannten Bedingungen des Problems berücksichtigt habe: die
Entfernung vom Erdmittelpunkt zum Mondmittelpunkt, den Radius der Erde, die Masse der Erde, die Masse des Mondes, kann ich die Anfangsgeschwindigkeit unseres Projektils mit der einfachsten Formel genau bestimmen.
- Wie lautet die Formel?
- Aber du siehst. Aber nur ich werde die von unserer Hülle zwischen Mond und Erde beschriebene Kurve angesichts ihrer relativen Bewegung um die Sonne nicht streichen. Angenommen, beide Planeten sind bewegungslos. Das wird völlig ausreichen.
- Warum?
- Da auf diese Weise die als „Drei-Körper-Aufgaben“ bezeichneten Aufgaben gelöst werden, ist die integrale Methode zur Lösung solcher Probleme noch nicht ausreichend entwickelt.Nach einer Weile wurde auch die Formel eingeführt, die den Lesern vorgestellt wurde:Dabei ist r der Radius der Erde, der Abstand zwischen den Erdmittelpunkten und dem Mond, x der Abstand des Kerns von der Erde. V 0 ist die Anfangsgeschwindigkeit des Kerns. V ist die Geschwindigkeit in einem Abstand von x.Und der Flug sah so ausHier möchte ich darauf hinweisen, dass diese Formel mit den angegebenen Anfangsdaten tatsächlich wahr ist. Und es zeigt den Gravitationseffekt der Erde und des Mondes auf das Gerät zu jedem Zeitpunkt wirklich genau an. Es ist ziemlich einfach, sich aus dem Energieerhaltungsgesetz abzuleiten.Ableitung der Verne-Garce-Formel
mv2 / 2 – γMm/R – γMm/R =const
m M,M – , ,
γ – , R - , R-
. .
mv2 / 2 – γMm/x– γMm/(D-x) =mv02 / 2 – γMm/r – γMm/(d-r)
m,
v2 / 2 –v02 / 2=γM/x+ γM/(D-x)– γM/r – γM/(d-r)
1/2*(v2-v02 )=γM(1/-1/r+M/M*1/(d-x)-M/M*1/(d-r))
1/2*(v2-v02 )=γM/r(r/-1+M/M(r/(d-x)-r/(d-r))
mg=mγM/r2 γM=g*r2
1/2*(v2-v02 )=gr(r/-1+M/M(r/(d-x)-r/(d-r))
Also, was ist los? Das Problem ist, dass die Dynamik des Systems nicht berücksichtigt wird. Der Mond dreht sich mit einer Geschwindigkeit von ca. 1 km / s um die Erde. Dies ist genau das Problem dieses Problems. Wenn die Station nach dem obigen Schema fliegt und zu einem neutralen Punkt zwischen Erde und Mond fliegt, wird sie vom Mondfeld überhaupt nicht erfasst, da dieses mit einer Geschwindigkeit von einem Kilometer pro Sekunde vom Projektil wegfliegt und das Projektil auf die Erde fällt. Aber dann gab es Hoffnung, dass die Erfassung des Geräts durch den Mond dennoch stattfinden würde, und ein ähnliches Schema zeigt in erster Näherung genau die Dynamik des Fluges. Mit der leichten Hand von Jules Verne wurde eine ähnliche Methode zur Berechnung des Fluges bald sehr beliebt. Es wurde nicht nur in Kunstbüchern verwendet, sondern auch in ernsthaften wissenschaftlichen Arbeiten.Es sollte beachtet werden, dass die Astronomen damals nur verstanden haben, wie wichtig es ist, die Dynamik zu berücksichtigen. Ja, und Differentialgleichungen, die sowohl die Schwerkraft als auch die Dynamik berücksichtigen, könnten dann leicht zusammengestellt werden. Nur konnte auch keine einfache Lösung finden. Tatsächlich hat das Drei-Körper-Problem, wie jetzt bekannt ist, keine allgemeine analytische Lösung. Das Problem konnte nur numerisch gelöst werden, was eine sehr, sehr große Anzahl von Routineberechnungen bedeutete, die Monate oder sogar Jahre des Lebens in Anspruch nehmen konnten. Zum Zeitpunkt der Veröffentlichung des Romans wurde ein ähnliches Problem nur zweimal numerisch gelöst. Darüber hinaus war der erste Versuch mehr als hundert Jahre vor der Veröffentlichung des Romans im Jahre 1759.Es ist bekannt, dass Edmund Halley, der einen Katalog von Kometen zusammenstellte, bemerkte, dass mehrere Kometen, die zu unterschiedlichen Zeiten am Himmel erschienen, sehr ähnliche Parameter haben. Nachdem er sie überprüft hatte, entschied er, dass es der gleiche Komet sein könnte. Dann wird sie bei seinem Namen genannt. Der Komet Halley erschien 1531, 1607 und 1682 am Himmel. Das heißt, die Auflagenzeit betrug 75-76 Jahre, und der Wissenschaftler sagte das nächste Auftreten für 1758 voraus. Und alles wäre wunderbar, wenn nicht ein "aber": Zum geschätzten Zeitpunkt tauchte der Komet am Himmel nie auf.Dann beschloss der französische Mathematiker Cleo, seine Flugbahn so genau wie möglich zu berechnen. Einschließlich der Berücksichtigung von Störungen seiner Flugbahn aufgrund der Attraktivität von Jupiter und Saturn. Es war eine sehr anstrengende und lange Arbeit, obwohl er diese Arbeit nicht alleine erledigte: Er wurde vom Astronomen J. Lalande und der Mathematikerin Madame Lepot unterstützt. Es stellte sich heraus, dass der Unterschied zu früheren Schätzungen der Revolutionsperiode des Kometen 618 Tage beträgt und am 13. April 1759 sein Perihel erreichen wird. Mit einem möglichen Fehler für einen Monat. Die Einschätzung erwies sich als sehr genau: Der Komet hat am 12. März sein Perihel passiert. Es war sowohl ein Sieg für Mathematiker als auch eine sehr gute Bestätigung von Newtons Gesetzen.Über diese Berechnung schrieb Laland später: "Wir haben sechs Monate von morgens bis abends gerechnet, manchmal ohne vom Essen aufzuschauen, und die Folge davon war, dass ich meine Gesundheit für den Rest der Tage meines Lebens gestört habe. Madame Lepots Hilfe war so, dass wir es ohne sie niemals wagen würden, diese enorme Arbeit zu leisten, die darin bestand, die Entfernung des Kometen von zwei Planeten - Jupiter und Saturn - für jeden Grad der Himmelskugel 150 Jahre lang zu berechnen. "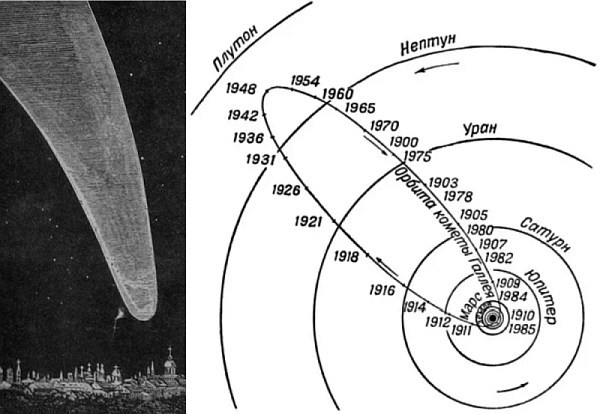
Sie können die Flugbahn von Halleys Kometen relativ zu den Umlaufbahnen sehen von Planeten Daszweite Mal wurde 1829 eine ähnliche Methode angewendet, erneut bei der Berechnung der Flugbahn des Halleyschen Kometen. Schätzungen zufolge wurde der Komet am 15. November 1835 zur Sonne zurückgebracht. Der Komet kehrte am 16. November nur einen Tag zu spät zurück.Infolgedessen hat eine ähnliche numerische Methode ihre Genauigkeit bewiesen. Anhand der obigen Geschichte können Sie jedoch deutlich erkennen, wie viel und langwierige Arbeit erforderlich war. Sechs Monate Arbeit von drei Mathematikern dauerten, um nur eine Flugbahn mit bekannten Anfangsparametern zu berechnen! Um jedoch die Flugbahnen eines Fluges von der Erde zum Mond zu berechnen, mussten Dutzende, wenn nicht Hunderte von Flugbahnen mit unterschiedlichen Anfangsparametern ausgewertet werden. Andernfalls ist es unmöglich, beispielsweise die genaue Geschwindigkeit, das Startdatum, die Flugbahnmerkmale, mögliche Fehler, Flugparameter der Station in der Nähe des Mondes usw. zu ermitteln. Dies kann Jahre dauern. Das heißt, diese Lösung wurde als sehr schwierig angesehen. Besonders für eine Aufgabe, die dann nicht viel praktische Bedeutung hat.Gleichzeitig bestand damals auch das Vertrauen, dass eine analytische Lösung für das Dreikörperproblem gefunden werden könnte. Zumindest in erster Näherung erlauben, die Flugparameter zu bewerten.Und die von Jules Verne vorgeschlagene Methode schien eine Antwort auf diese Frage zu geben. Schließlich war er mathematisch im Rahmen anfänglicher Annahmen einwandfrei. Ja, er hat die Dynamik nicht berücksichtigt, aber dann erwarteten viele, dass diese Annahme normal war und die reale Flugbahn des Projektils von der Erde zum Mond ungefähr so aussehen würde.Berechnung aus dem Buch „Raumschiffe. (Interplanetare Kommunikation in den Fantasien von Schriftstellern) “1928Und die mathematische Schönheit, gepaart mit der großen Popularität des Romans, spielte einen grausamen Witz: Mit dieser Methode bewerteten praktisch alle Pioniere der Weltraumforschung - Goddard , Sternfeld , Obert , Max Valle und viele andere - den Flug . Manchmal, äußerst selten, schätzten sie auch keinen Direktflug, sondern die Ellipse des Erdsatelliten. Diese Methode hatte aber auch Nachteile. Zum Beispiel waren sich viele aus irgendeinem Grund sicher, dass es ausreichte, um in den Aktionsbereich zu fallen, um den Mond zu erreichen. weiter, sagen sie, sollte die Anziehungskraft des Mondes den Rest erledigen. Obwohl, wie oben gesagt, die Möglichkeit, im Dreikörperproblem herumzufliegen, bereits bewiesen wurde.Ein gutes Beispiel wäre Werner von Brauns Artikel in der Wochenzeitschrift vom 18. Oktober 1952, in dem von Braun beschrieb, wie seiner Meinung nach eine Expedition zum Mond aussehen würde.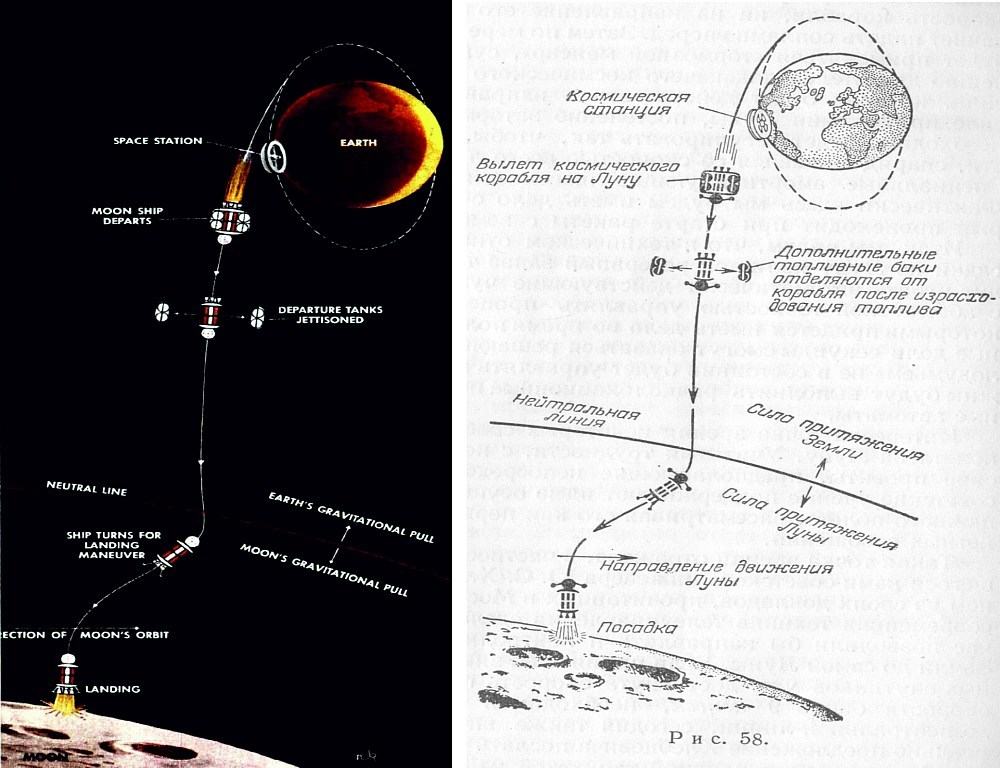
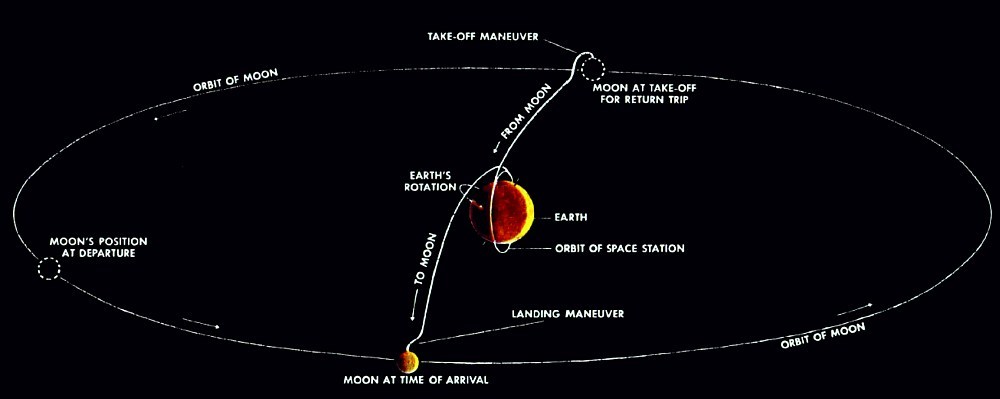Der Artikel selbst kann hier heruntergeladen werden.Aus der Abbildung ist deutlich ersichtlich, dass genau das Schema von Jules Verne dort vorgestellt wird: Erstens eine neutrale Region zwischen Erde und Mond erreichen und anschließend unter dem Einfluss seiner Anziehung auf den Mond fallen. Die Kanone wurde lange Zeit durch eine Rakete ersetzt, aber das Grundprinzip ist unverändert geblieben. Obwohl seit der Veröffentlichung des Romans fast hundert Jahre vergangen sind.Doch bald begann sich die Herangehensweise an Flüge von der Erde zum Mond zu ändern. Einschließlich dank der Entwicklung elektronischer Computer.Fortsetzung folgt .