Im November verwirrte das Quanta-Magazin seine Leser mit Fragen zum Zeichnen von Formen aus identischen flachen Objekten (wie Münzen oder Dominosteinen). Dieser Artikel enthält sowohl Fragen als auch detaillierte Antworten darauf.Frage 1
, , . . . , , ? n ?
Physikalisch erfordert die Aufgabe das Ausbalancieren des Drehmoments der Figur auf beiden Seiten der Tischkante. Das Drehmoment jeder Seite ist das Produkt aus der Masse dieser Seite und dem Abstand vom Massenmittelpunkt zur Kante. Wenn der Schwerpunkt der gesamten Figur über der Kante liegt, wirkt auf beiden Seiten das gleiche Moment, und das Gesamtsystemdrehmoment ist Null. Für ein zusammengesetztes Objekt kann das Gesamtdrehmoment für jede Fläche ermittelt werden, indem das Drehmoment aller Komponenten addiert wird. Daher können wir die ursprüngliche Aufgabe teilen und regieren, wobei wir nur die Änderungen berücksichtigen, die auftreten, wenn ein neuer Block zu einem vorhandenen Stapel hinzugefügt wird, so etwas wie eine mathematische Induktion (nennen wir es physikalische Induktion).Stellen Sie sich einen Stapel von n-1 Blöcken vor, von denen jeder eine Gewichtseinheit wiegt und eine Länge von einer Längeneinheit hat. Der Stapel ist am Rand des Tisches ausgeglichen. Stellen Sie sich vor, die Sichtlinie ist entlang der Tischkante gerichtet und der Tisch befindet sich links - das heißt, die hängenden Enden der Blöcke ragen nach rechts heraus. Da der Stapel an der Kante ausbalanciert ist, befindet sich der Schwerpunkt direkt über der Kante und sein Drehmoment ist Null. Stellen Sie sich nun vor, wir hätten den gesamten Stapel vertikal angehoben und einen weiteren Block darunter platziert, sodass seine rechte Kante bündig mit der Tischkante war. In der Praxis kann dies schwierig sein, aber in einem Gedankenexperiment ist es einfach.Wir haben dem Stapel etwas Stabilität verliehen, indem wir den n-ten Block von unten hinzugefügt haben, da sich der Schwerpunkt des gesamten Stapels leicht nach links verschoben hat. Bezeichne diesen Versatz x. n Blöcke wiegen n Einheiten und haben ein gemeinsames Drehmoment x * n um die nach links gerichtete Tischkante. Denken Sie daran, dass ein Stapel von n-1 Blöcken ein Gesamtmoment von Null hat. Wir haben nur den Moment des neuen Blocks hinzugefügt - mit einer Masse von einer Masseneinheit und mit einem Abstand zum Massenmittelpunkt von der Tischkante in einer halben Längeneinheit.Es stellt sich heraus, dass x * n = 1/2 ist, was x = 1 / 2n bedeutet, wobei x der Abstand zum neuen Massenmittelpunkt vom Rand des Tisches ist.Das heißt, wenn Sie den gesamten Stapel von n Blöcken um 1/2 Länge nach rechts verschieben, wird er am Rand perfekt ausbalanciert - und dies ist die maximal mögliche Verschiebung. Um den Aufbau der Induktion abzuschließen, stellen wir fest, dass der maximale Überhang des ersten Blocks von der Tischkante 1/2 Längeneinheit beträgt.Daher ersetzen wir für fünf Blöcke in der Formel n jede Ebene von 1 bis fünf, um den maximalen Überhang zu erhalten:x=1/2+1/4+1/6+1/8+1/10=137/120=1,141(6)
Es ist ersichtlich, dass, wenn Sie von oben beginnen und dann Blöcke nach unten hinzufügen, jede Verschiebung die Hälfte des Kehrwerts der Anzahl der verfügbaren Blöcke beträgt. Solche Folgen von inversen Zahlen sind als harmonische Reihen bekannt. Eine solche Reihe divergiert langsam, und wenn n gegen unendlich tendiert, neigt sie auch gegen unendlich.Die allgemeine Summenformel für n Blöcke wird durch Summieren aller Mitglieder der Reihe erhalten. Es stellt sich heraus, dass die Hälfte des n-ten harmonischen Terms wie folgt geschrieben werden kann:Frage 2
Stellen Sie sich vor, Sie haben dieselben fünf Blöcke und möchten ganz oben an einem Punkt, der ein Viertel der Länge des Blocks vom hängenden Ende entfernt ist, etwas Dekoration darauf platzieren. Alle Blöcke wiegen eine Gewichtseinheit und der Schmuck wiegt ein Fünftel des Blocks. Was ist jetzt die maximale Überhanglänge? Wie ändert dies die Grundformel?
Betrachten Sie zunächst den ersten Block, auf dem die Dekoration steht und so liegt, dass seine rechte Kante bündig mit der Tischkante abschließt. Der Schwerpunkt des Blocks ohne Dekoration ist eine halbe Längeneinheit von der Tischkante entfernt. Die Dekoration verschiebt sie beispielsweise um x nach rechts. Die Masse der Dekoration beträgt 1/5 und der Abstand zum neuen Schwerpunkt beträgt 1/4. Wir setzen die Momente gleich und erhalten x = 1/5 * (1/4 x), daher ist x = 1/24. Aufgrund der Dekoration muss der erste Block um 1/24 der Länge nach links verschoben werden, sodass der maximale Überhang jetzt 11/24 statt 1/2 beträgt.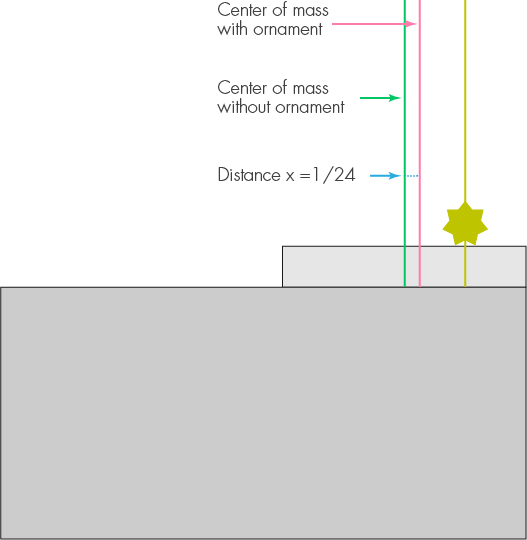
Frage 3
, , . . . , . , , . , ?
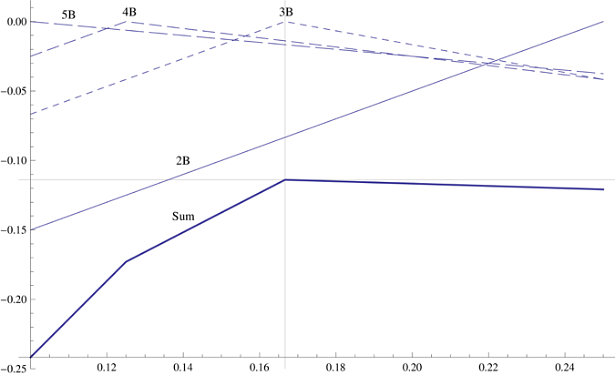
Da die Wahrscheinlichkeit, zwei bis fünf Blöcke zu haben, gleich ist, müssen Sie den Betrag maximieren, der den maximalen Überhang für diese vier Fälle angibt. Für einen Stapel von 2-5 Blöcken gibt es eine optimale Position des ersten Blocks, was den maximalen Überhang des gesamten Stapels ergibt. Wenn Sie für jede der vier möglichen Größen des nächsten Stapels den größten Überhang im Diagramm erstellen, erhalten Sie zwei Liniendiagramme und zwei Diagramme in Form eines invertierten V. Ihre Eckpunkte geben die optimale Startposition des Anfangsblocks für Stapel mit 3-4 Blöcken an. Wenn wir die Diagramme zusammenfassen, erhalten wir das Gesamtüberhangdiagramm, das die Richtung in jeder der vier optimalen Positionen dramatisch ändert. Es stellt sich heraus, dass der beste Gesamtüberhang in der optimalen Position für die drei Blöcke erreicht wird, wonach der Graph abfällt. Daher müssen Sie den ursprünglichen Block unter der Annahme platzierendass Sie drei zusätzliche Blöcke erhalten und der Überhang 1/6 Längeneinheiten beträgt.