Wie man unmögliche Hintergrundbilder macht: eine Geschichte verbotener Symmetrien

Auf der linken Seite befindet sich ein Tapetenmuster mit Rotationssymmetrie sechster Ordnung um jede der braun-grünen Rosetten. Auf der rechten Seite befindet sich ein Tapetenmuster mit Spiegelsymmetrie in Bezug auf horizontale Linien, die durch jedes elliptische Element eines Buntglasfensterornaments verlaufen.

Auf den ersten Blick ist es nicht schwieriger, eine Tapete zu erfinden, als Aufgaben aus einem Kindergarten zu erledigen. Designer können eine beliebige Kombination von Farben und Formen für das Originalstück auswählen und es einfach in zwei Richtungen multiplizieren. Abhängig vom Muster des Anfangsstücks und der Wahl der Richtungen können zusätzliche Symmetrien auftreten - beispielsweise Symmetrie sechster Ordnung im ersten Bild oder Spiegelsymmetrie im zweiten Bild. Beide Muster wurden vom Mathematiker Frank Farris von der University of California in Santa Clara erstellt.


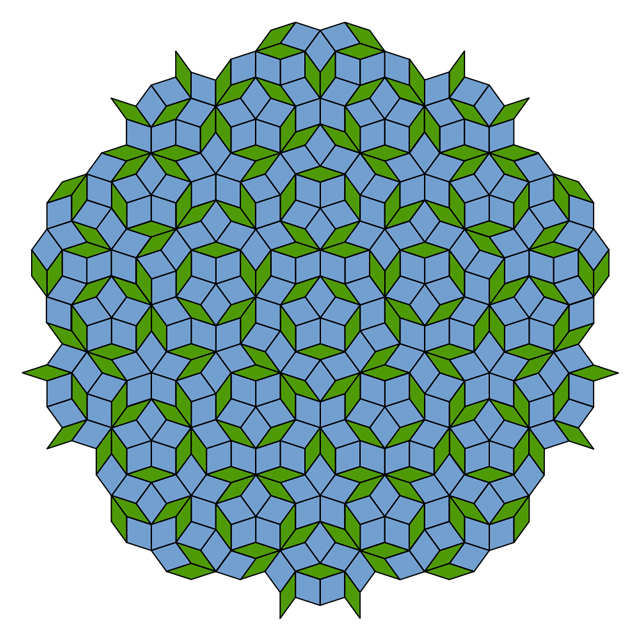Penrose-Kacheln zeigen viele Beispiele für lokale Symmetrie fünfter Ordnung, aber sie haben keine Wiederholungen des Musters. Wenn Sie große Flächen in der Ebene füllen, nähert sich das Verhältnis der Anzahl der breiten Kacheln zur Anzahl der schmalen Kacheln dem goldenen Schnitt.

Obwohl es möglich ist, Tapeten mit Rotationssymmetrien zweiter, dritter, vierter oder sechster Ordnung herzustellen, ist es unmöglich, Tapeten mit Symmetrie fünfter Ordnung zu erstellen [die Reihenfolge zeigt, wie oft sich das Muster während einer 360 ° -Drehung selbst ausrichtet - ca. übersetzt.]. Diese Einschränkung ist Mathematikern seit fast 200 Jahren als „kristallographische Einschränkung“ bekannt. Die Geometrie des Fünfecks verbietet Muster mit Symmetrie fünfter Ordnung. Gleiches gilt für Bestellungen ab sieben.

Die interessantesten Muster, wie z. B. Penrose-Kacheln, zeigen jedoch an vielen Stellen und in verschiedenen Maßstäben lokale Symmetrie fünfter Ordnung, nur ohne sich wiederholende Muster. Mit einer anderen Methode als dem Penrose-Ansatz hat Farris die ungewöhnliche Symmetriegeometrie fünfter Ordnung gebremst und einen neuen Satz aufregender Bilder erstellt - Pseudotapeten, die auf den ersten Blick nicht der kristallografischen Einschränkung zu entsprechen scheinen.


Abb. 4 Die

vierte Figur sieht aus wie ein Gegenbeispiel für eine kristallographische Beschränkung mit Rotationssymmetrie fünfter Ordnung um Punkt A, während das Muster in einer Ebene in die Richtungen AB oder AC verschoben werden kann. Tatsächlich schreibt Faris in seinem Artikel für die Zeitschrift Notices of the American Mathematical Society, dass dieses Bild nur eine clevere Fälschung ist.

"Sie wissen, dass die Symmetrie, die Sie beobachten, unmöglich ist", sagt Stephen Kennedy vom Carleton College in Minnesota.

Rotationssymmetrie fünfter Ordnung um Punkt A scheint erfüllt zu sein. Wenn Sie jedoch genau hinschauen, werden Sie feststellen, dass sich die Räder um die Punkte B und C geringfügig von A unterscheiden. Wenn wir uns vom Muster entfernen könnten, um mehr Wiederholungen zu sehen, wären die sichtbaren Wiederholungen des Musters immer weniger wie ein Muster im Bereich des Punktes Und selbst wenn immer überzeugendere Kopien von A an anderen Stellen erscheinen würden, wie in Abb. 5. Faris zeigte, dass solche Illusionen auch in größerem Maßstab erzeugt werden können, indem man sich vom Muster entfernt und es eine bestimmte Anzahl von Malen wiederholt - insbesondere die Anzahl, die Zahlen aus der Fibonacci-Reihe entspricht (1, 1, 2, 3, 5, 8, 13, 21, ... wobei jede folgende Zahl die Summe der beiden vorhergehenden ist), was auch eine Rolle in der Geometrie von Penrose-Kacheln spielt.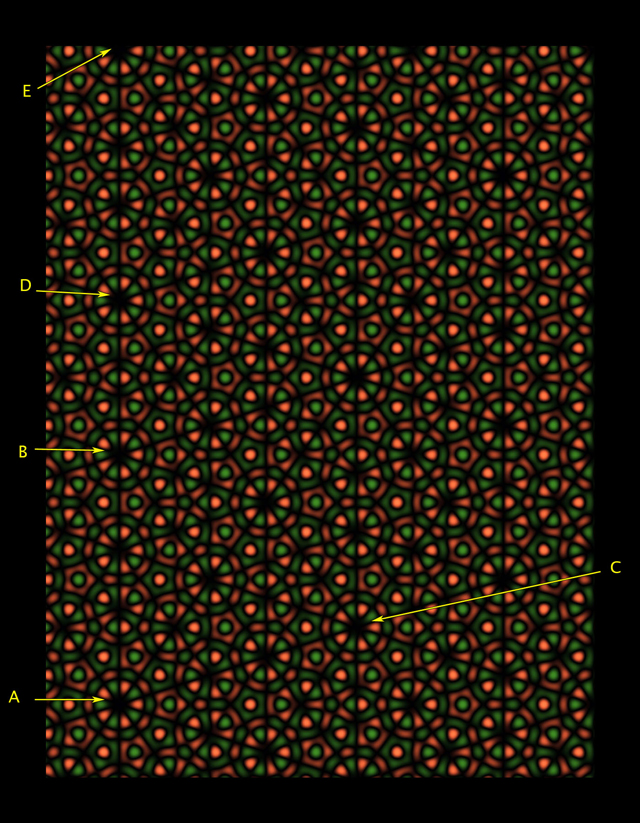


Abb. 5

"Wir verstehen, dass dies eine Art Täuschung ist", sagt Faris. Dennoch, wie er in dem Artikel schreibt, laden diese Bilder „unsere Augen ein, sie zu studieren und fast perfekte Wiederholungen zu genießen“.

Faris dachte an diese Fälschungen und veränderte die Technologie, mit der er echte Tapeten mit Rotationssymmetrie 3. Ordnung erstellte, wie in Abb. 6.

Um eine Symmetrie 3. Ordnung zu erzeugen, begann Faris mit der Arbeit im dreidimensionalen Raum, der eine besonders natürliche Rotation aufweist, indem er drei Raumkoordinaten sortiert und Punkte im Raum um 120 Grad um die Diagonale dreht. Dann erstellte Faris dreidimensionale Tapetenmuster, überlagerte speziell ausgewählte Sinuskurven und kombinierte sie mit einer vorgewählten Farbpalette. Die Punkte wurden in Abhängigkeit von ihrer Position auf überlagerten Sinuskurven gefärbt. Dann brachte Faris eine flache Tapete heraus, die diese Farbe auf eine zweidimensionale Ebene senkrecht zur Rotationsachse des ursprünglichen Raums beschränkte.

Dieser glatte, sinusförmige Ansatz zum Erstellen von Tapetenmustern unterscheidet sich von der herkömmlichen Methode zum Kopieren und Einfügen, sagt Kennedy. "Dies ist eine sehr neue Methode, um symmetrische Muster zu erstellen."


Abb. 6

Das gleiche Verfahren im fünfdimensionalen Raum hätte anscheinend zur Erzeugung eines Musters mit Symmetrie fünfter Ordnung führen müssen - wenn wir nur nicht gewusst hätten, dass dies unmöglich ist. Interessanterweise, dachte Faris, an welchem ​​Punkt versagt dieses System?

Theoretisch ist ein fünfdimensionaler Raum möglich, obwohl er schwer vorstellbar ist. Er hat ein natürliches Analogon der Rotationssymmetrie fünfter Ordnung wie im dreidimensionalen Raum - die Symmetrie der dritten. Im fünfdimensionalen Raum kann eine von zwei Ebenen ausgewählt werden, von denen jede senkrecht zur Rotationsachse und zur anderen Ebene ist. Jeder von ihnen kann um einen Punkt um 72 oder 144 Grad gedreht werden. Es mag schwierig erscheinen, sich zwei Ebenen und eine gerade Linie senkrecht zueinander vorzustellen, aber in fünf Dimensionen haben alle genug Platz.

Faris verstand das Problem: Wenn eine senkrechte Ebene den dreidimensionalen Raum genau durchschneidet und unendliche Hintergrundbilder mit einer unendlichen Anzahl von Punkten mit ganzzahligen Koordinaten enthält, sind zwei senkrechte Ebenen im fünfdimensionalen Raum irrational und enthalten keine Punkte mit ganzzahligen Koordinaten (mit Ausnahme des Referenzpunkts). . Da das aus Sinuskurven erzeugte Tapetenmuster durch Verschiebungen um ganze Zahlen wiederholt wird, erben solche Ebenen keine Muster von Räumen höherer Ordnung.

"So erscheint die Fliege in der Suppe", schreibt Faris in dem Artikel.

Trotzdem erscheint auf diesen beiden Ebenen dank der Beteiligung der sogenannten Tapete die Illusion der Struktur der Tapete der goldene Schnitt, eine irrationale Zahl, die die Richtungen zweier Ebenen beschreibt, und Fibonacci-Zahlen.

Dank ihrer Beziehungen konnte Faris zeigen, dass es zwar keine Punkte mit ganzzahligen Koordinaten auf zwei Ebenen gibt, jeder von ihnen jedoch der unendlichen Streuung von Punkten mit ganzzahligen Koordinaten sehr nahe kommt, deren Koordinaten Fibonacci-Zahlen sind. Jedes Mal, wenn sich die Ebene einem dieser Fibonacci-Punkte nähert, sieht das Muster fast genauso aus wie am Referenzpunkt, wodurch die Illusion einer exakten Kopie entsteht.



Faris fand auch heraus, wie man die Farben und Muster von Naturfotos mit Wellenfunktionen kombiniert, um sie in die Gestaltung von Mustern einzubeziehen, wodurch man eine große Anzahl von "gefälschten" Hintergrundbildern erhalten kann. In der obigen Abbildung sehen Sie die Zweige der Bäume, die vom Foto abgewandert sind.

Source: https://habr.com/ru/post/de400591/