Wichtige Tautologien in der Wissenschaft. Teil 1. Physik

Wissen Sie, was eine logische Tautologie ist? Sie wissen es wahrscheinlich. Und falls Sie dies nicht wissen, wird der Autor versuchen, dieses Konzept jetzt zu erklären. Wir werden nicht anfangen, zur trockenen und formalen Sprache der Mathematik zu wechseln, wir werden keine seelenlosen Pedanten wie Wikipedia sein, und wir werden im übertragenen Sinne sagen: Eine Tautologie ist eine Art Ouroboros, der seinen eigenen Schwanz beißt. Zum Beispiel "nichts ist, wenn es nichts gibt" oder "Objekte, die schmal und niedrig genug sind, um durch diese Tür zu gelangen, passieren sie leicht" und dergleichen. Solche Aussagen sind immer wahr und enthalten grob gesagt keine neuen Informationen. Überraschenderweise enthalten einige wichtige Gesetze und Prinzipien der Wissenschaft verborgene Tautologien, die jedoch ihre Bedeutung und Richtigkeit nicht beeinträchtigen. Interessant? Dann mach weiter, unter dem Schnitt!

Kaiser Sarlac Grant Scenticus III war gelangweilt. Sehr langweilig. Wenn er Langeweile verspürte, spielte er normalerweise Steine ​​(ein ziemlich einfaches, aber kniffliges Spiel, ähnlich wie bei unseren Checkern, Reversi und Go ). Heute kam jedoch keiner der Philosophen, die normalerweise mit ihm spielten. Er saß da ​​und starrte eine der Positionen an.

Grants interner Experimentator beschloss, die Anzahl der möglichen Positionen zu zählen. Lassen wir es an diesem Ort und zählen wir selbst.

Gemäß den Regeln dürfen bis zu 3 Steine ​​auf einer Zelle sein. Insgesamt gibt es 6 Steine ​​(3 für jeden Spieler). Wir werden nicht die Anzahl aller möglichen Positionen berücksichtigen. Es ist viel interessanter zu berechnen, auf wie viele Arten Sie eine Position festlegen können. Aber schauen Sie sich zuerst die Zeichnung an.

Der Einfachheit halber betrachten wir nur eine Zelle. Die obige Position kann zum Beispiel auf drei Arten erhalten werden, die sich darin unterscheiden, welche Steine ​​wir auf die Tafel gelegt haben: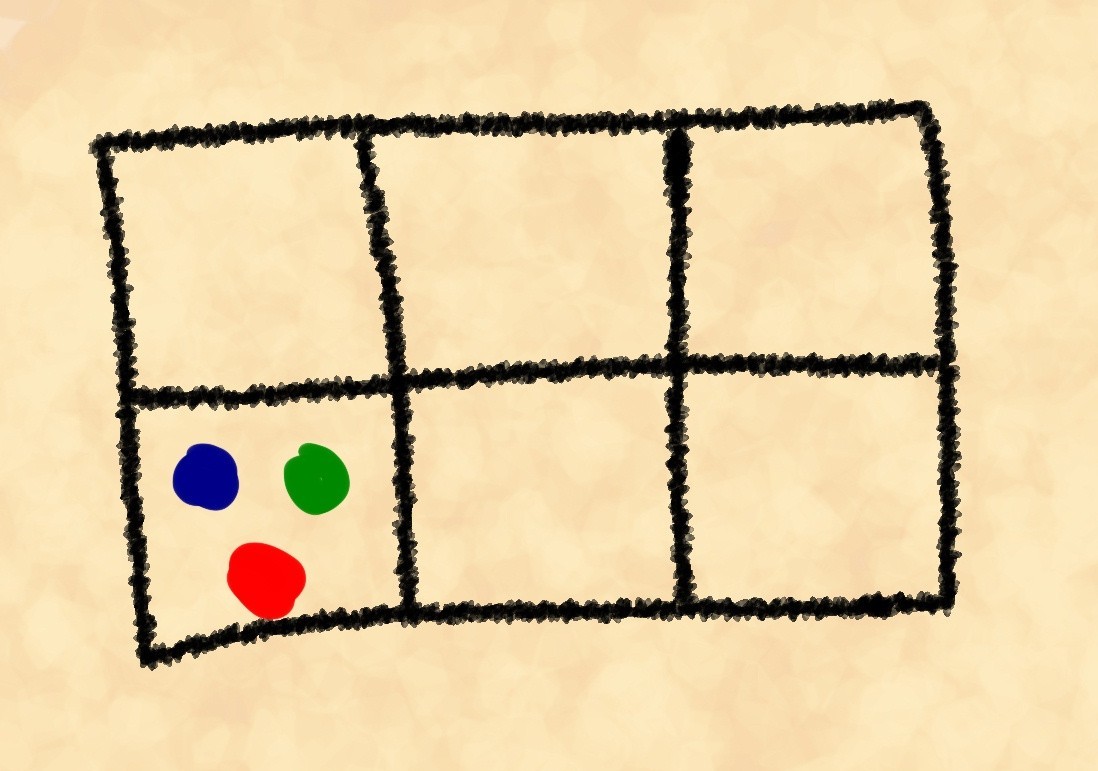

  

Wir haben die Steine ​​bedingt bemalt, damit wir sie voneinander unterscheiden können. Offensichtlich gibt es viel mehr als drei Methoden. Aber wie viel genau? Den ersten der drei Steine ​​können wir auf sechs Arten auswählen. Jede dieser sechs Optionen wird mit der Auswahl des zweiten Steins aus den verbleibenden fünf und des letzten der verbleibenden vier fortgesetzt. Wir haben$$ , aber gleichzeitig haben wir Wiederholungen zugelassen, zum Beispiel sind Rot-Blau-Gelb, Gelb-Rot-Blau und Blau-Rot-Gelb die gleiche "Berechnung". 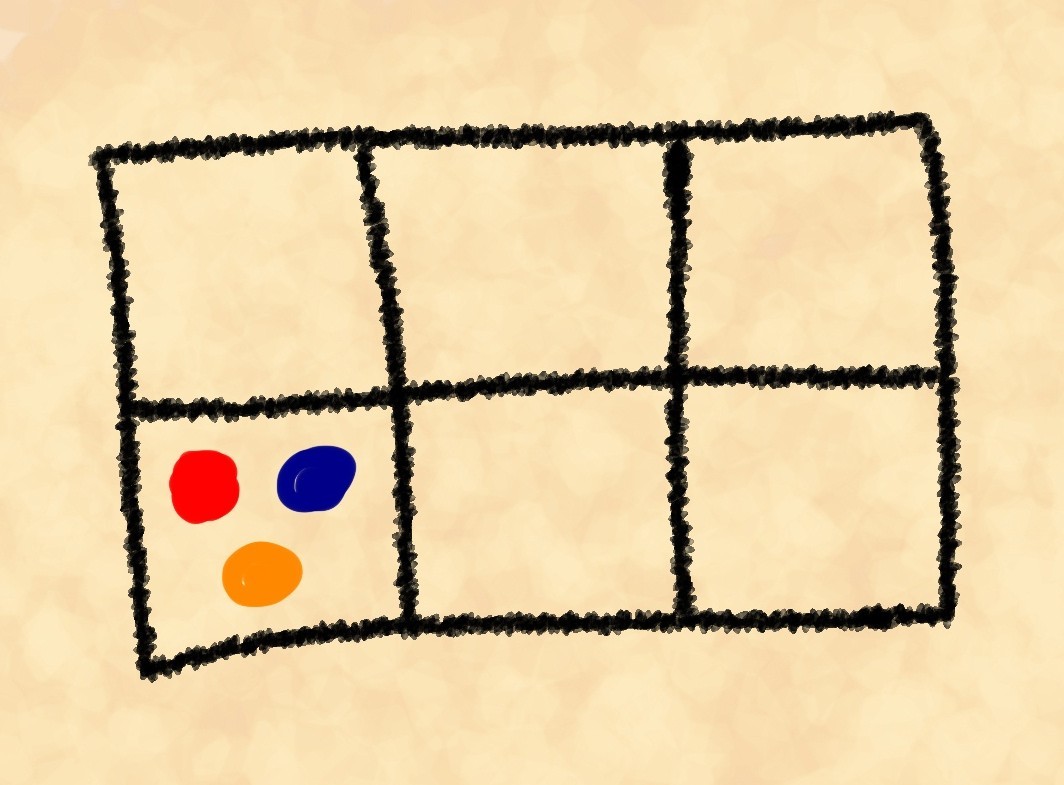Um die Anzahl der Wiederholungen zu ermitteln, geben wir an, auf wie viele Arten wir drei gleichfarbige Steine ​​auf dem Brett auslegen können. Der erste kann einer der drei notwendigen Steine ​​sein, der zweite sollte einer der verbleibenden zwei sein, der dritte wird der letzte Stein sein, den wir brauchen:$6\cdot5\cdot4=120$

$$. Als Ergebnis haben wir 120/6 = 20 Möglichkeiten, die Steine ​​in der erforderlichen Weise auszulegen. Nennen wir diese Nummer das Gewicht dieser Position. Natürlich hat es nichts mit körperlichem Gewicht zu tun, nur dieser Name wird in der Statistik allgemein akzeptiert. Lassen Sie uns die Aufgabe komplizieren. Berechnen wir die Gewichte dieser Positionen: Wenn Sie zu faul sind, um all diese Mathematik zu verstehen, überspringen Sie den nächsten Absatz. Erste Position:$3\cdot2\cdot1=6$




  

1. Wir verteilen 2 Steine ​​auf einer der beiden linken Zellen: $$$2\cdot6\cdot5/2=30$
2. In der zweiten Zelle legen wir zwei Steine ​​aus den restlichen 4 aus: $$$4\cdot3/2=6$
3. Insgesamt haben wir $$$30\cdot6/2=90$.

$$$30\cdot4\cdot3/2=180$$$. In allen Fällen wird eine Teilung durchgeführt, um Wiederholungen zu vermeiden.$4\cdot6\cdot3\cdot5\cdot2\cdot4\cdot3/24=360$

Wir haben also die folgenden Gewichte: 90 für das erste Layout, 180 für das zweite und 360 für das dritte. Haben Sie bemerkt, dass das Gewicht umso geringer ist, je schlanker die Position ist? Seine Majestät Grant bemerkte dies. Und jetzt wird er das Gewicht für echte Spielpositionen berechnen.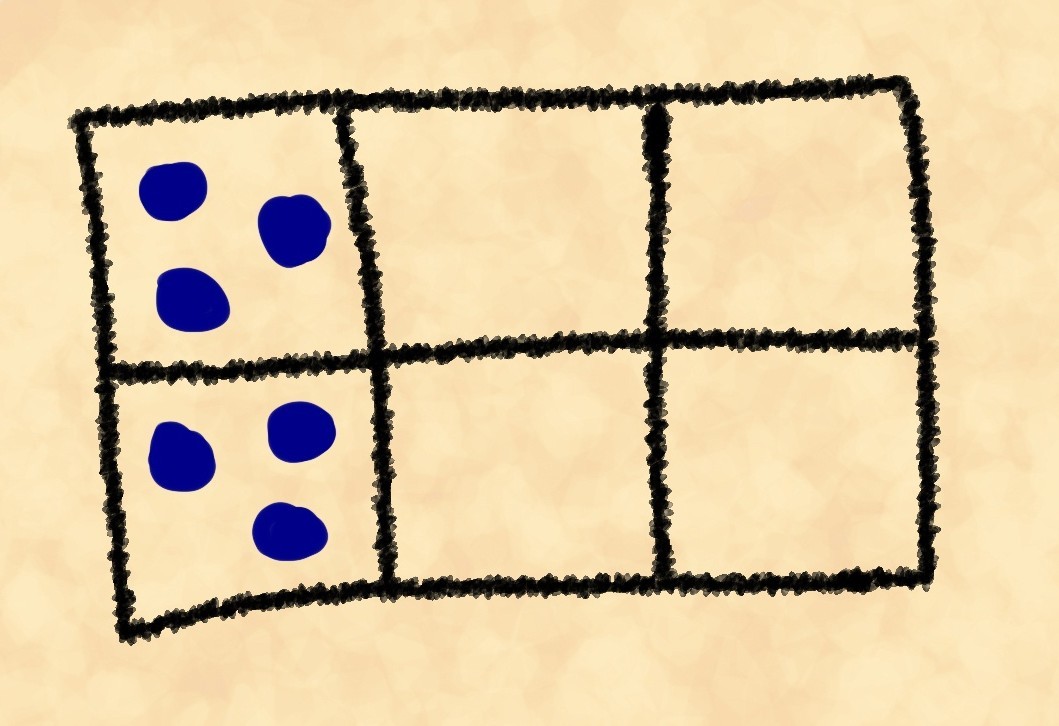

  

Er stellt sich als 90, 360 und 720 heraus. Hier endet jedoch seine Geduld (wie wahrscheinlich Ihre). Er drückt das Brett verärgert, streut zufällig die Steine ​​und bemerkt den Philosophen Klofzus, der an der Tür steht.

„Sag es mir, Philosoph“, fragt er mit einem Hinweis auf Unzufriedenheit, „warum fliegen die Steine ​​zufällig und gleichmäßig um das Brett herum und passen nicht zu drei in einen Käfig vom Rand?

Als Antwort darauf lächelte Klofzius und sagte:

"Ich habe Ihre Berechnungen eine Weile beobachtet, Overlord, und Sie könnten diese Frage wahrscheinlich bereits selbst beantworten." Aber ich sage immer noch: Steine ​​können auf neunzig verschiedene Arten am Rand des Bretts bestellt werden, und siebenhundertzwanzig können über alle Zellen verteilt werden. Bei Steinen gibt es viel mehr Möglichkeiten, gleichmäßig über das Brett zu verteilen, als am Rand gesammelt werden.

Vielleicht verlassen wir hier Sarlak. Aber achten Sie auf Klofzus 'Erklärung: Steine ​​streuen auf dem Brett, weil es viel mehr Möglichkeiten gibt, sie gleichmäßig zu verteilen, als sie ordentlich auszulegen. Und der Unterschied zwischen der Anzahl der Methoden (das Gewicht der Steinlayouts) ist umso größer, je größer das Brett und die Anzahl der Steine ​​ist. Für eine Platte mit 15 Zellen (3 mal 5) und 15 Steinen beträgt das Gewicht eines vollständig geordneten Layouts (3 Steine ​​in einer Zelle entlang einer Kante) ungefähr 1,4 Millionen (wenn genau 1.401.400) und für eine Uniform (einer in jeder Zelle) ungefähr 1,3 Billiarden das heißt, fast eine Million Mal mehr. Daher ist es in diesem Fall viel einfacher, ein Durcheinander zu bekommen, als eine Bestellung zu bekommen. Man erinnert sich unwillkürlich an eine so wundervolle Aussage: „Die Eier brechen bei jedem Schritt, aber niemand hat jemals gesehen,so dass die Fragmente eines zerbrochenen Eies zusammenkommen und ein ganzes Ei werden. Und das alles, weil es nur einen Weg gibt, ein ganzes Ei zu bekommen, und unendlich viele Wege, um zerbrochen zu werden. “

Um die Regelmäßigkeit zusammenzufassen, die wir festgestellt haben:

In jedem Prozess, der für sich allein ohne zusätzlichen externen Einfluss abläuft, ist es am wahrscheinlichsten, dass das Ergebnis erzielt wird, das auf vielfältigste Weise erzielt werden kann.

Schauen Sie genauer hin, es ist eine Tautologie in ihrer ganzen Pracht. Um die Dinge zu vereinfachen, versichere ich einfach, dass "das, was einfacher ist, öfter passiert". Es ist jedoch auch eines der wichtigsten physikalischen Gesetze. Viele von Ihnen haben wahrscheinlich bereits verstanden, dass es sich um den zweiten Hauptsatz der Thermodynamik handelt. Schauen wir uns eine seiner „offiziellen“ Formulierungen an: Die

Entropie eines geschlossenen Systems kann nicht abnehmen.

Das ist weniger wie eine Tautologie, oder? Aber was für ein kluges Wort ist Entropie?

Stellen wir uns vor, die Luft füllt einen Raum. Es besteht aus einer Vielzahl von Molekülen. Wenn wir den Raum mental in Zellen aufteilen, erhalten wir ein dreidimensionales Analogon des Steinspiels auf einem sehr großen Brett mit einer großen Anzahl von Steinen. Jede Position des Spiels wird in diesem Fall als Makrostatus des Systems bezeichnet. Jedes der Layouts von Steinen, die eine bestimmte Position implementieren, ist ein Mikrozustand . Wir nehmen zwei Zahlen: die Anzahl aller Mikrozustände, die diesen Makrostaten realisieren, und die Anzahl aller möglichen Mikrozustände. Wenn wir den ersten in den zweiten teilen, erhalten wir die Wahrscheinlichkeit dieses Makrostaten.

Definition aus dem Buch: Die Entropie des Zustands eines Systems ist der Logarithmus der Wahrscheinlichkeit dieses Zustands.

Wir übersetzen es in eine Sprache, die Grant versteht - die Entropie einer Position ist der Logarithmus des Gewichts einer bestimmten Position. Lassen Sie uns versuchen, dies noch deutlicher zu machen: Je mehr Möglichkeiten Sie finden, desto mehr Entropie.

Jetzt sehen wir, dass die Buchformulierung des zweiten Prinzips Folgendes sagt: Von einer Position an sich kann nur ein Übergang zu einer Position erfolgen, die auf mehr als oder mit der gleichen Anzahl von Pfaden wie der ursprüngliche erhalten werden kann.

Versuchen wir es zu vereinfachen: Wenn wir das Brett schütteln, bekommen wir eher eine Position, die leichter zu bekommen ist.

Es scheint, dass wir wieder zur Tautologie gekommen sind. Selbst wenn es sich um eine Tautologie handelt, ist das zweite Prinzip eines der wichtigsten physikalischen Gesetze. Darüber hinaus ist dies das einzige Gesetz der Physik, das uns sagt, dass die Zeit in eine bestimmte Richtung fließen sollte, was den Unterschied zwischen Vergangenheit und Zukunft ausmacht.

Lassen Sie uns zum Schluss noch ein paar Formulierungen des zweiten Anfangs sehen:

• Clausius-Postulat: Ein kreisförmiger Prozess ist unmöglich, dessen einziges Ergebnis die Übertragung von Wärme von einem weniger erhitzten Körper auf einen Wärmer ist
• Thomsons Postulat: Ein kreisförmiger Prozess ist unmöglich, dessen einziges Ergebnis die Produktion von Arbeit durch Kühlung des Wärmespeichers wäre.

Wie Sie sehen, gibt es keine Tautologie mehr. Und keiner von ihnen ist offensichtlich. Es kann jedoch gezeigt werden, dass diese beiden Formulierungen vollständig der tautologischen „es ist höchstwahrscheinlich, dass etwas wahrscheinlicheres passiert“ entsprechen. Manchmal müssen wir uns zuerst etwas Offensichtliches bewusst werden, um etwas Neues zu lernen.

Im nächsten Teil werden wir eine andere „wissenschaftliche Tautologie“ betrachten, die auf den ersten Blick gegen den zweiten Hauptsatz der Thermodynamik verstößt.

Source: https://habr.com/ru/post/de400803/