Moon Duchin, außerordentlicher Professor für Mathematik und Direktor des Programms für Wissenschaft, Technologie und Gesellschaft an der Tufts University (USA)

Politische Parteien und Wahlkommissionen in den USA, Russland und anderen Ländern „betrügen“ traditionell mit der Größe und Form von Wahlkreisen und versuchen, den Protestteil der Wählerschaft in getrennten Vorbehalten zu isolieren oder im Gegenteil einen kleinen Abstrich in benachbarten Wahlkreisen zu verbreiten. Aufgrund solcher Manipulationen - Jerrymandering - erhalten die Bezirke manchmal sehr bizarre Umrisse. Aber alles ist legal. Bisher gibt es keine normale Gesetzgebung mit mathematischen Formeln, die die geometrische Form des Bezirks beschreiben. Der außerordentliche Professor für Mathematik an der Tufts University beabsichtigt, diesen Mangel zu beheben, und bietet verschiedene mathematische Modelle an.

Jerrymandering wird häufig in Ländern mit mehrheitlichen Parlamentswahlen und einem starken Parteiensystem eingesetzt. Damit die maximale Anzahl „ihrer eigenen“ Abgeordneten ins Parlament gelangt, konzentrieren sich die Wähler der Oppositionspartei auf mehrere Wahlkreise, während sie im Übrigen einen kleinen, aber selbstbewussten Vorteil für ihre Partei erzielen. Aus diesem Grund werden Wahlkreise mit einer ungleichen Anzahl von Wählern sowie Wahlkreise mit einer bizarren territorialen Form geschaffen.

In den USA wurde beispielsweise Jerrymandering eingesetzt, um schwarze Wähler zu neutralisieren, damit ihre Kandidaten nicht ins Parlament gingen (es gab Fälle positiver Diskriminierung, wenn schwarze Kandidaten auf diese Weise befördert wurden). Und in Russland wurde 2015 vor den Parlamentswahlen ein Gesetz zum „Blütenblatt“ -Schnitt von Bezirken verabschiedet, in dem kleine Sektoren großer Städte mit illoyalen Wählern große ländliche Gebiete mit einer loyalen Bevölkerung verbinden. Infolgedessen erfüllt Jerrymandering die gleiche Aufgabe - es blockiert in den meisten Distrikten den Durchgang „böswilliger“ Kandidaten zum Parlament.

In der Region Nowosibirsk beispielsweise teilten die Behörden die Bevölkerung der Stadt in vier Teile auf und verbanden sie jeweils mit dem Gebiet der Region.


Wahlbezirke der Region Nowosibirsk

In den Vereinigten Staaten ist die Situation mit Jerrymandering noch schlimmer, da in den meisten Staaten die Kürzung von Distrikten in die Zuständigkeit der regionalen Parlamente fällt (dh in der Hand der Partei mit parlamentarischer Mehrheit). Zum Beispiel ist die Region Nowosibirsk in ihrer Idiotie nicht einmal der Verteilung von Maryland auf acht Grafschaften nahe.


Zweiter Bezirk pcs. Maryland


Dritter Bezirk pcs. Maryland

Darüber hinaus enthalten staatliche Verfassungen in der Regel nur Grundregeln für die Form von Wahlkreisen oder überhaupt keine Regeln. Es wird normalerweise angegeben, dass der Bezirk „kompakt“ sein sollte, aber dies ist eindeutig eine breite, subjektive Aussage.

Um die Situation zu ändern, gründete Moon Dachin eine fünfköpfige Expertenorganisation, die Metric Geometry and Gerrymandering Group (MGGG), die eine Mailingliste eröffnete, um das Problem des Jerrymandering in der wissenschaftlichen Gemeinschaft zu erörtern. Sie beschrieb die Ziele der Organisation in einem Interview mit der Zeitschrift Chronicle of Higher Education.

Was ist Kompaktheit?

Associate Professor Dachin schlägt vor, die Möglichkeit in Betracht zu ziehen, verschiedene Konzepte zu verwenden, um die akzeptable Form des Distrikts zu beschreiben, dh das in den Staatsverfassungen festgelegte Erfordernis der "Kompaktheit" objektiv zu überprüfen.

Sie können beispielsweise einen Parameter wie den Polsby-Popper-Score berücksichtigen, der als Verhältnis der Fläche eines Landkreises zur Fläche eines Kreises berechnet wird, dessen Länge dem Umfang des Landkreises entspricht.


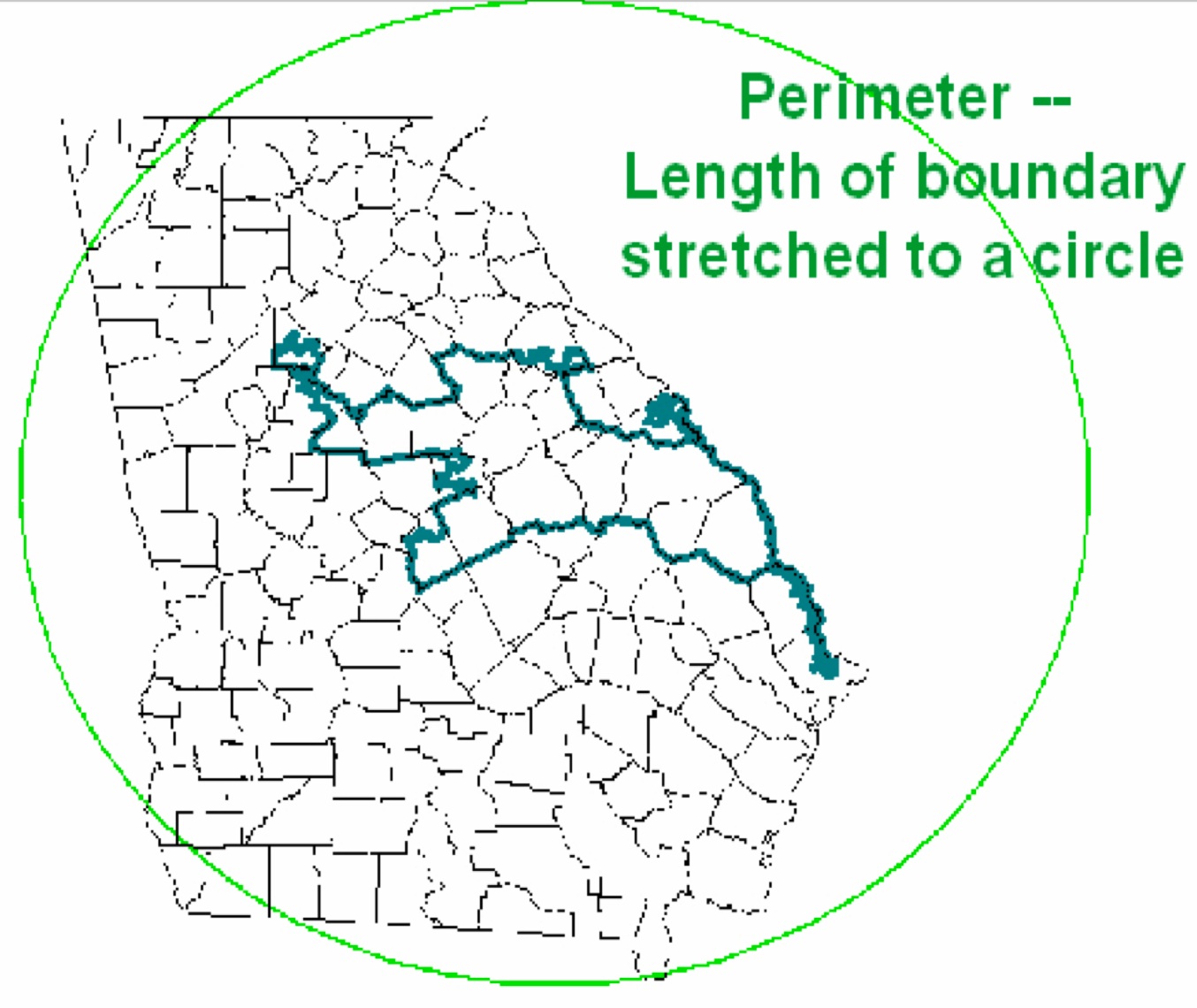Polsby Popper Score

Eine andere Option ist ein einfaches Verhältnis der Fläche des Bezirks zur Fläche des Kreises im umschriebenen Kreis.


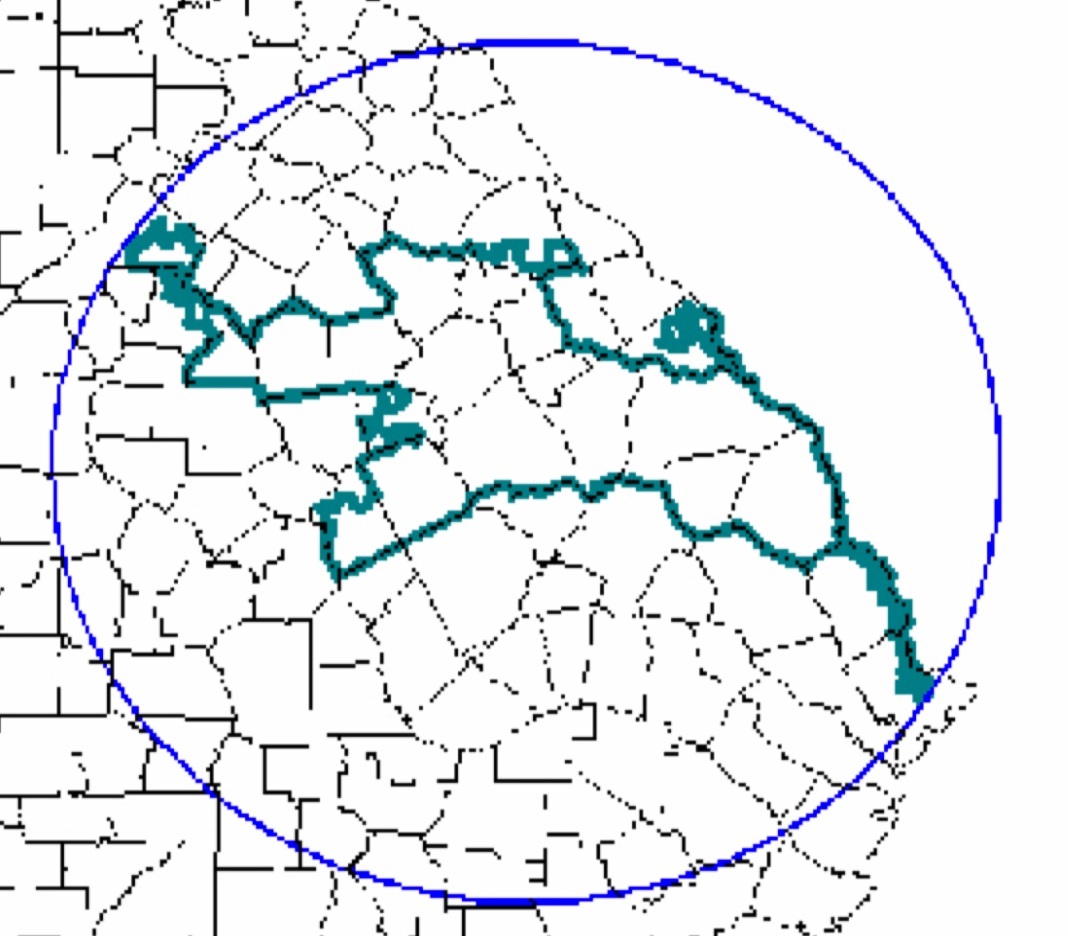Das Verhältnis der Fläche des Bezirks zur Fläche des Kreises

Moon Dachin sagt, er arbeite derzeit an metrischen Geometrieproblemen im Rahmen der geometrischen Gruppentheorie . Dies ist ein Bereich der Mathematik, der endlich erzeugte Gruppen unter Verwendung der Verbindungen zwischen ihren algebraischen Eigenschaften und den topologischen und geometrischen Eigenschaften der Räume, auf die solche Gruppen wirken, oder der Gruppen selbst, die als geometrische Objekte betrachtet werden, untersucht. Auf Danchins persönlicher Website finden Sie mehrere wissenschaftliche Arbeiten in diesem Bereich, in denen sie einen solchen Parameter als den durchschnittlichen Abstand zwischen allen Punkten einer beliebigen Figur beschreibt (wahrscheinlich muss der Parameter noch normalisiert werden, beispielsweise durch den Durchmesser desselben umschriebenen Kreises). Dieser Parameter ist als Merkmal der Kompaktheit durchaus geeignet.

Eine weitere Option zur Bewertung der Kompaktheit, die Experten scherzhaft erwähnen, ist der Grofman-Interokulartest, den der amerikanische Wissenschaftler Bernie Grofman vorgeschlagen hat. Mit diesem Test können Sie den Grad des Gerrymandering visuell bestimmen, indem Sie messen, wie weit die Augen einer Person sind, die auf die Karte schaut, und das Ausmaß des Betrugs bewerten. Übrigens wurde einmal der gleiche Test angeboten, um den "Hardcore" -Porno zu bewerten. Der Punkt ist, dass es schwierig ist, solche Dinge zu formalisieren, aber wenn Sie es sehen, verstehen Sie es sofort (sehen Sie sich noch einmal die Grafschaften in Maryland an).

Der außerordentliche Professor an der Tufts University ist zuversichtlich, dass mit Hilfe der Mathematik viele soziale Probleme gelöst werden können. Die Schwierigkeit besteht jedoch darin, dass Politiker einfache mathematische Konzepte oft nicht verstehen können. Daher wird es ziemlich schwierig sein, sie davon zu überzeugen, solche Formeln in die Gesetze und die Verfassung des Landes aufzunehmen. Schließlich müssen sie zuerst verstanden werden. Moon Dachin gibt ein Beispiel für das Konzept der mangelnden Effizienz , das Jerrymandering anhand einfacher Beispiele beschreibt - ein einzigartiger Fall, in dem ein US-Richter die Mathematik verstand und sagte, dass er sie „mochte“. Dieses mathematische Dokument bildete die Grundlage des Whitford v. Nichol in Wisconsin. So sollten mathematische Konzepte erklärt und Richtern, Politikern und der Gesellschaft präsentiert werden: so klar und überzeugend wie möglich.