Wie man in einem Superfluid schwimmt

Wie wir wissen, stoppt jeder Körper, der in einer Flüssigkeit schwimmt, früher oder später aufgrund der Kräfte der viskosen Reibung, wenn seine Bewegung von keinem Motor unterstützt wird. Es gibt jedoch Flüssigkeiten, sogenannte Superfluide, bei denen keine viskose Reibung vorliegt ^(*) . Das bekannteste Beispiel für ein Superfluid ist flüssiges Helium , das auf mindestens 2,17 Grad über der absoluten Nulltemperatur abgekühlt ist.

Die Bewegung ohne Viskosität zeigt sich in vielen beeindruckenden Effekten: Superfluides Helium fließt leicht durch die engsten Risse und Risse, kann endlos in einem Kreis ^(**) fließen und durch einen sehr dünnen Flüssigkeitsfilm, der an seinen Wänden haftet, aus einem Gefäß herausfließen. Alle diese Phänomene sind Beispiele für großräumige Quanteneffekte.

In einem kürzlich erschienenen theoretischen Artikel wurde die Frage behandelt: Ist es möglich, in einer superfluiden Flüssigkeit zu schwimmen? Mit anderen Worten, kann ein hypothetischer Schwimmer, der seine Arme und Beine bewegt, eine Zugkraft erzeugen, die es ihm ermöglicht, ohne die Kraft der viskosen Reibung zu beschleunigen oder zu verlangsamen?

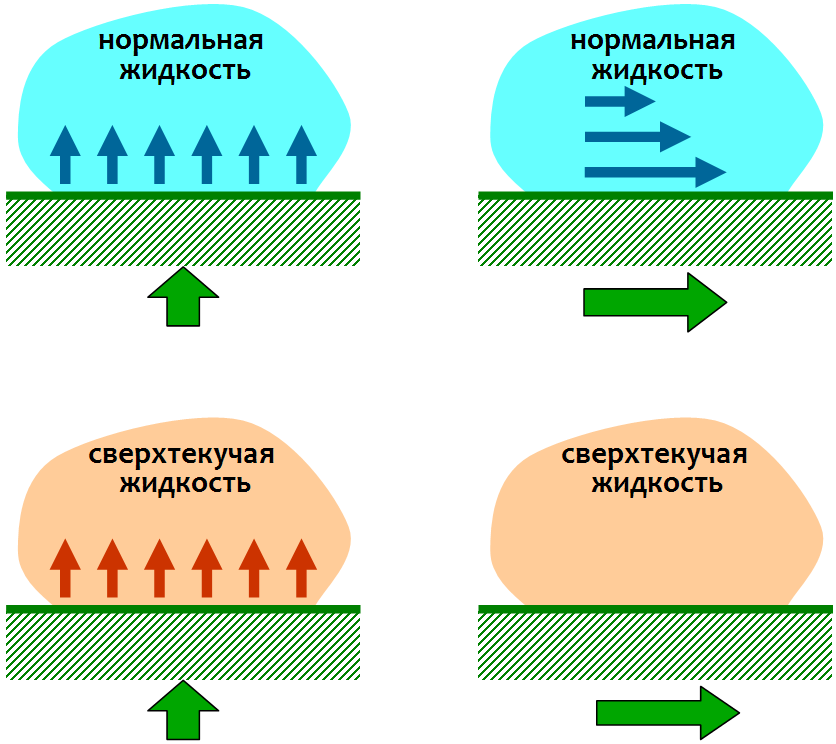
Man kann die Nicht-Trivialität der Antwort auf diese Frage erkennen, indem man das Verhalten normaler und superfluider Flüssigkeiten im Zusammenspiel mit Körpern betrachtet. Wie in der Figur gezeigt, kann eine normale Flüssigkeit in Bewegung gebracht werden, indem sie sowohl mit der Oberfläche eines festen Körpers gedrückt als auch aufgrund viskoser Reibungskräfte mit sich selbst gezogen wird. In einer superfluiden Flüssigkeit funktioniert letztere nicht: Es gibt keine Reibung darin und sie kann nur gedrückt werden, was, wie wir sehen werden, einige Schwimmmethoden unmöglich macht.



Um die allgemeinen Prinzipien physikalischer Phänomene zu analysieren, ist es üblich, einfache Modelle von "kugelförmigen Pferden im Vakuum" zu betrachten. Der zur Diskussion stehende Artikel ist keine Ausnahme: Er betrachtete Zwei- und Dreikörpermodelle als „Schwimmer“, bei denen es sich um zwei und drei Ellipsoide handelt, die durch „Gelenke“ verbunden sind. Schwimmer können ihre Ellipsoide bewegen, Gelenke biegen und lösen. Wenn es dem Schwimmer gelingt, sich von der umgebenden Flüssigkeit abzudrücken, schafft er Traktion und beginnt sich zu bewegen.



Ein Zweikörperschwimmer sieht aus wie eine Muschel und kann versuchen zu schwimmen, indem er den Winkel zwischen seinen Ellipsoiden regelmäßig ändert wie ein Schmetterling, der mit den Flügeln schlägt. Berechnungen zeigen jedoch, dass er nicht schwimmen kann: Mit einer Welle bewegt sich der Schwimmer hin und her, bleibt aber im Durchschnitt an Ort und Stelle ( hier können Sie ein Video seiner einfachen Bewegungen sehen).


Oben: Dichteprofil der superfluiden Flüssigkeit zu verschiedenen Zeitpunkten. Die blauen Bereiche, aus denen die Flüssigkeit herausgedrückt wird, sind Ellipsoide eines Zweikörperschwimmers.
Unten: Schwimmerkoordinate als Funktion der Zeit.


Zwischen diesen Ergebnissen und Purcells Jakobsmuschelsatz können Parallelen gezogen werden . Dieser wichtige Satz der Schwimmtheorie besagt, dass eine Muschel, die ihre Schale langsam in einer viskosen Flüssigkeit öffnet und schließt, nirgendwo schwimmt, solange ihre Bewegungen zeitlich reversibel sind. Letzteres bedeutet, dass das periodische Öffnen und Schließen der Shell-Klappen ihr Aussehen nicht ändert, wenn die Zeit in die entgegengesetzte Richtung beginnt (Sie können sich ein Video vorstellen, das wie bei der normalen Wiedergabe rückwärts gerichtet aussieht). In unserem Fall hat die Flüssigkeit keine Viskosität und es funktioniert nicht der Satz von Purcell, sondern das Analogon für eine superfluide Flüssigkeit.


Zeichnung aus einem Bericht von Edward Purcell (Nobelpreisträger für Physik 1952).

Die Situation ändert sich, wenn ein Zweikörperschwimmer seine Ellipsoide häufiger schwingt. Wenn ihre Geschwindigkeit die Schallgeschwindigkeit in einer Flüssigkeit überschreitet, werden Schallwellen und Wirbel ^(***) emittiert. Diese Erregungen bringen einen gewissen Impuls mit sich, der den Schwimmer aufgrund des Rückstoßes in Bewegung versetzt. Die Abbildung zeigt, dass in diesem Fall die Koordinate schwankt, aber insgesamt mit der Zeit abnimmt, was bedeutet, dass sich der Schwimmer von rechts nach links bewegt. Nach zehn Schwankungen (rechts von der gestrichelten Linie in der Grafik) stoppt die Klappe und der Schwimmer bewegt sich durch Trägheit weiter ( Video ).



Sie können eine andere Art der Bewegung des Schwimmers ausprobieren, wenn sich seine Flügel schließen und nicht nur in die richtige Richtung, sondern abwechselnd in zwei Richtungen auseinander bewegen. Solche symmetrischen Bewegungen ähneln dem Flügelschlag eines Schmetterlings. Berechnungen zeigen, dass in diesem Fall viele quantisierte Wirbel angeregt werden (sie sind in der Figur als kleine Kreise sichtbar), aber im Allgemeinen ist das Schwimmen nicht sehr effektiv. Der Grund dafür ist, dass ungefähr die gleiche Anzahl von Wirbeln angeregt wird, die sich sowohl nach rechts als auch nach links bewegen, und die von ihnen weggetragenen Impulse sich weitgehend gegenseitig aufheben ( Video ).



Betrachten Sie jetzt einen Drei-Körper-Schwimmer. Er hat einen wichtigen Vorteil gegenüber dem Zweikörper: Er kann sich winden und Serpentinenbewegungen ausführen, die nicht in sich selbst übergehen, wenn sich die Zeit umkehrt. Dies bedeutet, dass Purcells Theorem nicht auf ihn zutrifft und er auch mit langsamen Bewegungen schwimmen muss. Die in der Abbildung gezeigten Berechnungen bestätigen diese Vermutung: Beim Zappeln bewegt sich der Schwimmer sicher horizontal, während er sich leicht vertikal verschiebt ( Video ).


Oben: Dichteprofil der superfluiden Flüssigkeit zu verschiedenen Zeitpunkten. Die blauen Bereiche, in denen die Flüssigkeit herausgedrückt wird, sind die Ellipsoide des Dreikörperschwimmers.
Unten: horizontale (X) und vertikale (Y) Koordinaten des Schwimmers als Funktion der Zeit.

Welche Anwendung kann auf die erzielten Ergebnisse gefunden werden? Es scheint, dass die Aufgabe des Schwimmens in einem Superfluid in der Praxis nicht besonders relevant ist, aber es gibt einen Bereich, in dem es nützlich sein kann. In jüngster Zeit wurden aktiv Experimente zur Bose-Kondensation und Superfluidität ultrakalter Atomgase entwickelt, mit denen große Pläne zur Erstellung von Quantensimulatoren, Quantencomputern und zur experimentellen Modellierung exotischer Materiezustände bestehen. In solchen Systemen ist es möglich, Gerinnsel eines Superfluidgases einer Art zu erzeugen, die in ein Superfluidgas eines anderen Typs eingetaucht sind. Wenn wir den Haufen nach Bedarf verformen können (und dies kann mit Hilfe von Laserstrahlen geschehen), ist es möglich, diesen Haufen ausgehend vom umgebenden Gas schwimmen zu lassen. Die Abbildung zeigt die Berechnungen, die diese Möglichkeit demonstrieren: Wenn die Änderungen in der Form des Bündels nicht zeitlich reversibel sind, gelingt es ihm tatsächlich, sich zu bewegen ( Video ).



Wir sehen also, dass es notwendig ist, mit Bedacht in einer superfluiden Flüssigkeit zu schwimmen: Der Satz von Purcell garantiert, dass wir nicht schwimmen können, wenn unsere Bewegungen unserer Arme und Beine mit uns selbst übereinstimmen, wenn wir in die entgegengesetzte Richtung spielen. Um sich zu bewegen, müssen wir uns entweder schneller als der Ton bewegen (was problematisch ist) oder uns wie eine Schlange winden, wodurch die Umkehrbarkeit der Bewegungen in der Zeit gestört wird. Diese Schlussfolgerungen sind Mikroorganismen bekannt, die in einer viskosen Flüssigkeit schwimmen: Um den Satz von Purcell zu umgehen, müssen sie spiralförmig rotierende Flagellen verwenden, die Analoga des hier betrachteten Dreikörperschwimmers sind.

Nach dem Artikel :
Hiroki Saito, können wir in Superfluiden schwimmen ?: Numerische Demonstration des Selbstantriebs in einer Bose - Einstein-Kondensat, Journal der Physical Society of Japan 84, 114001 (2015).

^(*) Tatsächlich ist dies nicht ganz richtig: Jede echte superfluide Flüssigkeit kann als Kombination der „normalen“ und der superfluiden Komponente ( Zwei-Fluid-Modell ) dargestellt werden, und die normale Komponente verlangsamt den sich bewegenden Körper immer noch. Dies verhindert jedoch nicht, dass sich die Superfluidkomponente vollständig ohne Reibung bewegt.

^(**) In der Praxis kann sich der Kreisfluss von superfluidem Helium abschwächen, jedoch nicht aufgrund der Viskosität, sondern aufgrund des quantenmechanischen Prozesses - des Schlupfes quantisierter Wirbel. In den Experimenten wurde 18 Stunden lang keine merkliche Dämpfung beobachtet.

^(***) Wirbel, die in einem Superfluid entstehen, sind nicht nur Wirbel wie kleine Tornados, sondern quantisierte topologische Anregungen . Im Gegensatz zu gewöhnlichen Wirbeln können sie aufgrund der allmählichen Dämpfung des Flusses nicht einfach verschwinden.