Quantenverschränkung ohne Verwirrung - was ist das?

Einführung

Es sind viele populäre Artikel erschienen, die über Quantenverschränkung sprechen. Experimente mit Quantenverschränkung sind ziemlich spektakulär, aber nicht mit Preisen ausgezeichnet. Warum sind so interessante Experimente für den Laien für Wissenschaftler nicht von Interesse? Beliebte Artikel sprechen über die erstaunlichen Eigenschaften von Paaren verschränkter Partikel - die Exposition gegenüber einem führt zu einer sofortigen Änderung des Zustands des zweiten. Und was sich hinter dem Begriff „Quantenteleportation“ verbirgt, über den sie bereits zu sagen begonnen haben, dass er mit überluminaler Geschwindigkeit geschieht. Betrachten wir dies alles unter dem Gesichtspunkt der normalen Quantenmechanik.

Was kommt aus der Quantenmechanik?

Quantenteilchen können nach dem klassischen Lehrbuch von Landau und Lifshitz in zwei Arten von Zuständen vorliegen - rein und gemischt. Wenn ein Teilchen nicht mit anderen Quantenteilchen interagiert, wird es durch eine Wellenfunktion beschrieben, die nur von seinen Koordinaten oder Impulsen abhängt - dieser Zustand wird als rein bezeichnet. In diesem Fall folgt die Wellenfunktion der Schrödinger-Gleichung. Eine andere Option ist möglich - das Teilchen interagiert mit anderen Quantenteilchen. In diesem Fall bezieht sich die Wellenfunktion bereits auf das gesamte System wechselwirkender Teilchen und hängt von all ihren dynamischen Variablen ab. Wenn wir nur an einem Teilchen interessiert sind, kann sein Zustand, wie Landau vor 90 Jahren gezeigt hat, durch einen Matrix- oder Dichteoperator beschrieben werden. Die Dichtematrix folgt einer Gleichung ähnlich der Schrödinger-Gleichung



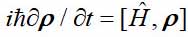
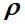
wo Ist die Dichtematrix, ist H der Hamilton-Operator und die Klammern bezeichnen den Kommutator.

Landau brachte ihn raus. Alle physikalischen Größen, die sich auf ein bestimmtes Teilchen beziehen, können durch eine Dichtematrix ausgedrückt werden. Dieser Zustand wird als gemischt bezeichnet. Wenn wir ein System wechselwirkender Partikel haben, befindet sich jedes der Partikel in einem gemischten Zustand. Wenn die Partikel über große Entfernungen verstreut sind und die Wechselwirkung verschwindet, bleibt ihr Zustand weiterhin gemischt. Befindet sich jedes von mehreren Partikeln in einem reinen Zustand, ist die Wellenfunktion eines solchen Systems das Produkt der Wellenfunktionen jedes Partikels (wenn die Partikel unterschiedlich sind. Für identische Partikel, Bosonen oder Fermionen ist es notwendig, eine symmetrische oder antisymmetrische Kombination zu bilden, siehe [1], aber später ist die Identität von Teilchen, Fermionen und Bosonen bereits eine relativistische Quantentheorie.

Ein verschränkter Zustand eines Partikelpaares ist ein Zustand, in dem eine konstante Korrelation zwischen physikalischen Größen besteht, die sich auf verschiedene Partikel beziehen. Ein einfaches und gebräuchliches Beispiel ist eine bestimmte physikalische Gesamtgröße, beispielsweise der Gesamtspin oder der Drehimpuls eines Paares. Ein Partikelpaar befindet sich in einem reinen Zustand, aber jedes der Partikel befindet sich in einem gemischten Zustand. Es scheint, dass eine Änderung des Zustands eines Partikels sofort den Zustand eines anderen Partikels beeinflusst. Auch wenn sie weit verstreut sind und nicht interagieren, wird dies in populären Artikeln zum Ausdruck gebracht. Dieses Phänomen wurde bereits als Quantenteleportation bezeichnet. Einige Analphabeten behaupten sogar, dass die Änderung sofort erfolgt, dh sich schneller als mit Lichtgeschwindigkeit ausbreitet.

Betrachten Sie dies aus quantenmechanischer Sicht: Erstens verstößt jede Aktion oder Messung, die den Spin oder den Drehimpuls nur eines Teilchens ändert, sofort gegen das Gesetz der Erhaltung der Gesamtcharakteristik. Der entsprechende Bediener kann nicht mit vollem Spin oder vollem Drehimpuls pendeln. Somit wird die anfängliche Verschränkung des Zustands eines Teilchenpaares verletzt. Der Spin oder das Moment des zweiten Teilchens kann nicht mehr eindeutig mit dem des ersten Teilchens assoziiert werden. Sie können dieses Problem von der anderen Seite betrachten. Nachdem die Wechselwirkung zwischen den Partikeln verschwunden ist, wird die Entwicklung der Dichtematrix jedes Partikels durch eine eigene Gleichung beschrieben, in der die dynamischen Variablen der anderen Partikel nicht enthalten sind. Daher ändert die Exposition gegenüber einem Partikel die Dichtematrix nicht gegenüber einem anderen.

Es gibt sogar den Satz von Eberhard [2], der besagt, dass die gegenseitige Beeinflussung zweier Teilchen nicht durch Messungen erfasst werden kann. Es gebe ein Quantensystem, das durch eine Dichtematrix beschrieben wird. Und lassen Sie dieses System aus zwei Subsystemen A und B bestehen. Der Satz von Eberhard besagt, dass keine Messung von Observablen, die sich nur auf Subsystem A beziehen, das Ergebnis der Messung von Observablen, die sich nur auf Subsystem B beziehen, nicht beeinflusst. Der Beweis des Theorems verwendet jedoch die Wellenreduktionshypothese eine Funktion, die weder theoretisch noch experimentell bewiesen wurde. Alle diese Überlegungen werden jedoch im Rahmen der nichtrelativistischen Quantenmechanik angestellt und beziehen sich auf verschiedene nicht identische Teilchen.

Diese Überlegungen funktionieren in der relativistischen Theorie bei einem Paar identischer Teilchen nicht. Ich möchte Sie noch einmal daran erinnern, dass die Identität oder Ununterscheidbarkeit von Partikeln aus der relativistischen Quantenmechanik stammt, bei der die Anzahl der Partikel nicht erhalten bleibt. Für langsame Teilchen können wir jedoch einen einfacheren Apparat der nichtrelativistischen Quantenmechanik verwenden, der einfach die Ununterscheidbarkeit von Teilchen berücksichtigt. Dann sollte die Wellenfunktion des Paares bezüglich der Permutation der Teilchen symmetrisch (für Bosonen) oder antisymmetrisch (für Fermionen) sein. Eine solche Anforderung ergibt sich in der relativistischen Theorie unabhängig von den Teilchengeschwindigkeiten. Diese Anforderung führt zu weitreichenden Korrelationen eines Paares identischer Partikel. Grundsätzlich kann sich ein Proton mit einem Elektron auch in einem verschränkten Zustand befinden. Wenn sie sich jedoch um mehrere zehn Angström zerstreuen, zerstört die Wechselwirkung mit elektromagnetischen Feldern und anderen Partikeln diesen Zustand. Die Austauschwechselwirkung (wie dieses Phänomen genannt wird) wirkt in makroskopischen Abständen, wie Experimente zeigen. Ein Teilchenpaar, das sogar meterweise verteilt ist, bleibt nicht zu unterscheiden. Wenn Sie eine Messung durchführen, wissen Sie nicht genau, zu welchem ​​Partikel der Messwert gehört. Sie messen gleichzeitig mit einem Partikelpaar. Daher wurden alle spektakulären Experimente mit genau den gleichen Teilchen durchgeführt - Elektronen und Photonen. Genau genommen ist dies nicht ganz der verwirrende Zustand, der im Rahmen der nichtrelativistischen Quantenmechanik betrachtet wird, sondern etwas Ähnliches.

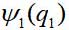
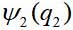
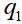
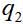
Betrachten Sie den einfachsten Fall - ein Paar identischer nicht wechselwirkender Partikel. Wenn die Geschwindigkeiten klein sind, können wir eine nichtrelativistische Quantenmechanik verwenden, wobei die Symmetrie der Wellenfunktion in Bezug auf die Permutation von Teilchen berücksichtigt wird. Lassen Sie die Wellenfunktion des ersten Teilchens , das zweite Teilchen - wo und - dynamische Variablen des ersten und zweiten Teilchens, im einfachsten Fall - nur die Koordinaten. Dann die Wellenfunktion des Paares



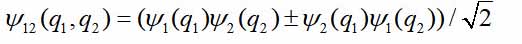
Die Zeichen + und - beziehen sich auf Bosonen und Fermionen. Angenommen, die Partikel sind weit voneinander entfernt. Dann lokalisiert in abgelegenen Gebieten 1 bzw. 2, dh außerhalb dieser Gebiete sind sie klein. Versuchen wir, den Durchschnittswert einer Variablen des ersten Partikels zu berechnen, beispielsweise die Koordinate. Der Einfachheit halber können wir uns vorstellen, dass nur Koordinaten in den Wellenfunktionen enthalten sind. Es stellt sich heraus, dass der Durchschnittswert der Koordinaten von Partikel 1 zwischen den Regionen 1 und 2 liegt und mit dem Durchschnittswert für Partikel 2 übereinstimmt. Dies ist tatsächlich natürlich - die Partikel sind nicht zu unterscheiden, wir können nicht wissen, welches Partikel Koordinaten hat. Im Allgemeinen sind alle Durchschnittswerte für Partikel 1 und 2 gleich. Dies bedeutet, dass wir durch Bewegen des Lokalisierungsbereichs von Partikel 1 (zum Beispiel wird das Partikel innerhalb des Defekts des Kristallgitters lokalisiert und wir bewegen den gesamten Kristall) auf Partikel 2 einwirken, obwohl die Partikel nicht im üblichen Sinne interagieren - beispielsweise durch ein elektromagnetisches Feld. Dies ist ein einfaches Beispiel für eine relativistische Verschränkung.

Aufgrund dieser Korrelationen zwischen den beiden Partikeln findet keine sofortige Informationsübertragung statt. Der Apparat der relativistischen Quantentheorie wurde ursprünglich so gebaut, dass sich Ereignisse in Raum-Zeit auf gegenüberliegenden Seiten des Lichtkegels nicht gegenseitig beeinflussen können. Einfach ausgedrückt, kein Signal, kein Einfluss oder keine Störung kann sich schneller ausbreiten als Licht. Beide Teilchen sind tatsächlich ein Zustand eines Feldes, zum Beispiel ein Elektronen-Positron. Indem wir an einem Punkt (auf Teilchen 1) auf das Feld einwirken, erzeugen wir eine Störung, die sich wie Wasserwellen ausbreitet. In der nicht-relativistischen Quantenmechanik wird die Lichtgeschwindigkeit als unendlich groß angesehen, was die Illusion einer augenblicklichen Veränderung erzeugt.

Die Situation, in der Partikel, die über große Entfernungen voneinander beabstandet sind, paarweise gekoppelt bleiben, erscheint aufgrund klassischer Vorstellungen von Partikeln paradox. Wir müssen uns daran erinnern, dass es in Wirklichkeit keine Teilchen gibt, sondern Felder. Was wir als Teilchen darstellen, ist einfach der Zustand dieser Felder. Die klassische Idee von Partikeln ist in der Mikrowelt völlig ungeeignet. Sofort stellen sich Fragen zu Größe, Form, Material und Struktur von Elementarteilchen. Tatsächlich entstehen mit einem Teilchen Situationen, die für das klassische Denken paradox sind. Beispielsweise fliegt im Stern-Gerlach-Experiment ein Wasserstoffatom durch ein inhomogenes Magnetfeld, das senkrecht zur Geschwindigkeit gerichtet ist. Der Spin des Kerns kann aufgrund der geringen Größe des Kernmagnetons vernachlässigt werden, wobei der Spin des Elektrons zunächst entlang der Geschwindigkeit gerichtet werden soll.



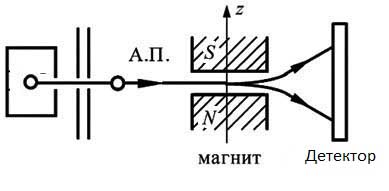
Die Entwicklung der Atomwellenfunktion ist leicht zu berechnen. Das anfängliche lokalisierte Wellenpaket wird in zwei identische Wellenpakete aufgeteilt, die symmetrisch in einem Winkel zur ursprünglichen Richtung fliegen. Das heißt, ein Atom, ein schweres Teilchen, das normalerweise als klassisch mit einer klassischen Flugbahn angesehen wird und in zwei Wellenpakete aufgeteilt ist, die sich zu vollständig makroskopischen Entfernungen streuen können. Gleichzeitig stelle ich fest - aus der Berechnung folgt, dass selbst ein ideales Stern-Gerlach-Experiment den Teilchenspin nicht messen kann.

Wenn der Detektor ein Wasserstoffatom beispielsweise chemisch bindet, werden die „Hälften“ - zwei Streuwellenpakete - zu einem zusammengesetzt. Wie eine solche Lokalisierung des verschmierten Partikels auftritt, ist eine separat existierende Theorie, in der ich nicht verstehe. Interessenten finden hier umfangreiche Literatur zu diesem Thema.

Fazit

Es stellt sich die Frage: Wozu dienen zahlreiche Experimente zum Nachweis von Korrelationen zwischen Partikeln in großen Entfernungen? Neben der Bestätigung der Quantenmechanik, an der kein normaler Physiker seit langem gezweifelt hat, ist dies eine spektakuläre Demonstration, die die Öffentlichkeit und Amateurbeamte beeindruckt, die Mittel für die Wissenschaft bereitstellen (zum Beispiel sponsert die Gazprombank die Entwicklung von Quantenkommunikationsleitungen). Für die Physik geben diese teuren Demonstrationen nichts, obwohl sie die Entwicklung experimenteller Techniken ermöglichen.

Literatur
1. Landau, L. D., Lifshits, E. M. Quantenmechanik (nichtrelativistische Theorie). - 3. Auflage, überarbeitet und ergänzt. - M.: Nauka, 1974.- 752 p. - ("Theoretische Physik", Band III).
2. Eberhard, PH, "Bell'scher Satz und die verschiedenen Konzepte der Nichtlokalität", Nuovo Cimento 46B, 392-419 (1978)