„Es gibt zwei identische Kugeln bei derselben Temperatur. Einer von ihnen liegt auf einer horizontalen Fläche, der andere ist an einem Faden aufgehängt. Beide Bälle melden die gleiche Wärmemenge. Werden die Bälle danach gleich sein oder nicht? (Jede Art von Wärmeverlust kann vernachlässigt werden.) "

Ein solches Problem tritt manchmal bei Olympiaden der Physik und der sozialen Medien auf . Die allgemein akzeptierte Antwort ist intuitiv: Aufgrund des Energieverbrauchs für die Wärmeausdehnung in Gegenwart der Schwerkraft ist eine auf einer horizontalen Oberfläche liegende Kugel kühler als an einem Faden zu hängen. Ein kürzlich veröffentlichter Artikel hat gezeigt, dass diese Antwort falsch ist. In der Tat wird das Ergebnis das Gegenteil sein: Der liegende Ball wird wärmer als der hängende. Wir werden verstehen, warum die traditionelle Methode zur Lösung dieses Problems zur falschen Antwort führt und warum uns die Intuition in diesem Fall stürzt.

Traditionelle Lösung und ihr Problem

Die traditionelle Lösung basiert auf der folgenden Argumentation. Beide Kugeln dehnen sich während des Erhitzens aus, wodurch der Schwerpunkt der auf einer horizontalen Fläche liegenden Kugel leicht ansteigt und der Schwerpunkt der hängenden Kugel abfällt. Infolgedessen erwärmt sich die liegende Kugel schwächer, da ein Teil der auf sie übertragenen Wärme beim Aufsteigen verbraucht wird und sich die hängende Kugel aufgrund der zusätzlichen Schwerkraft beim Absenken stärker erwärmt.


In der herkömmlichen Lösung verwendete Argumentation: Aufgrund der Wärmeausdehnung steigt die auf dem Tisch liegende Kugel an und die am Faden hängende Kugel wird abgesenkt.

Die Antwort kann durch eine einfache Formel für die liegende Temperaturdifferenz ausgedrückt werden ( $$ ) und hängen ( $$ ) Bälle:

$$

wo $$ , $$ und $$ - Masse, Radius und Wärmekapazität der Kugeln, $$ - die auf sie übertragene Wärmemenge, $$ - Erdbeschleunigung, $$ Ist der lineare Wärmeausdehnungskoeffizient des Materials der Kugeln, den wir für ausreichend klein halten. Wie gesehen $$ - Der liegende Ball wird kälter.

Es scheint, dass bei dieser Entscheidung alles logisch ist. Die „erste Schwalbe“, die zeigt, dass hier etwas nicht stimmt, ist ein mentaler Versuch, auf der Grundlage des Balls eine Wärmekraftmaschine zu schaffen.

Die Maschine kann wie folgt arbeiten: Erstens liegt der Ball auf dem Tisch, wo wir ihn erhitzen, wodurch sein Schwerpunkt steigt. Dann befestigen wir die Kugel am oben hängenden Faden und entfernen vorsichtig den Tisch, damit sich die Höhe der Kugel nicht ändert. Schließlich kühlen wir den Ball auf seine Anfangstemperatur ab, wodurch der Ball komprimiert wird und sein Schwerpunkt steigt. Fazit: Der Teil der Wärme, den wir beim Erhitzen auf den Ball übertragen haben, wurde in mechanische Arbeit umgewandelt, um ihn anzuheben, und dieser Zyklus kann endlos wiederholt werden.


Der Betriebszyklus einer kugelbasierten Wärmekraftmaschine: Nach dem Erhitzen und Abkühlen stieg die Kugel an, was bedeutet, dass wir einen Teil der Wärme in mechanische Arbeit umgewandelt haben.

Das Problem hierbei ist, dass durch Erhöhen des Radius der Kugel der Wirkungsgrad (Wirkungsgrad) einer solchen Maschine beliebig nahe an 100% gebracht werden kann. Dies widerspricht dem zweiten Hauptsatz der Thermodynamik , wonach der Wirkungsgrad einer Wärmekraftmaschine den Wirkungsgrad des Carnot-Zyklus bei gleichen Temperaturen von Heizung und Kühlschrank nicht überschreiten darf.

Was ist los?

Warum ist die traditionelle Lösung des Problems falsch? Hierbei ist zu berücksichtigen, dass der von Anfang an auf dem Tisch liegende Ball vor dem Erhitzen durch die Schwerkraft leicht abgeflacht und der hängende Ball leicht gedehnt wird. Dies wirkt sich negativ auf den Wirkungsgrad der oben beschriebenen Wärmekraftmaschine aus: Während der Federung wird die Kugel leicht abgesenkt, wodurch der Wirkungsgrad abnimmt und den Wirkungsgrad des Carnot-Zyklus nicht mehr überschreitet.


Die Wirkung der Schwerkraft auf die Kugeln: Die auf dem Tisch liegende Kugel wird abgeflacht und die am Faden hängende wird gedehnt.

Wie wird sich dies bei Betrachtung des ursprünglichen Problems manifestieren? Es stellt sich heraus, dass das Komprimieren oder Dehnen eines Materials seine Wärmekapazität ändert: Im Fall eines komprimierten Materials erfordert das Erhitzen auf dieselbe Temperatur weniger Wärme als im Fall eines gedehnten. Deshalb:

• Wenn der auf dem Tisch liegende Ball erhitzt wird, steigt ein Teil der Wärme aufgrund der Wärmeausdehnung an. Gleichzeitig wird das Erhitzen des Kugelmaterials selbst einfacher und erfordert weniger Wärme.
• Wenn eine an einem Faden hängende Kugel erhitzt wird, wird die Schwerkraft beim Absenken zu der auf sie übertragenen Wärme addiert. Gleichzeitig ist das Erhitzen des Kugelmaterials selbst zeitaufwändiger und erfordert mehr Wärme.

Bei der herkömmlichen Lösung werden nur Faktoren berücksichtigt, die durch weiße Pfeile angezeigt werden. Das Ignorieren der durch schwarze Pfeile angezeigten Faktoren führt zu einer falschen Antwort.

Wie wir sehen können, gibt es in beiden Fällen Faktoren, die sowohl für eine Antwortoption (ein liegender Ball kann sich als kühler als ein hängender herausstellen) als auch in die entgegengesetzte Richtung (ein liegender Ball kann sich als wärmer als ein hängender herausstellen) wirken. Welches überwältigt?

Es scheint, dass der Effekt der Änderung der Wärmekapazität eines Materials während des Zusammendrückens oder Zugens, selbst wenn er vorhanden ist, sehr gering sein sollte und vernachlässigt werden kann, wie dies bei der herkömmlichen Lösung des Problems der Fall ist. Dies ist jedoch nicht so. Dieser Effekt liegt in der Größenordnung der Wärmeausdehnung selbst, da beide Effekte auf der Anharmonizität interatomarer Kräfte beruhen. Die Berücksichtigung eines dieser Effekte in der herkömmlichen Lösung in Kombination mit dem Ignorieren des anderen ist inkonsistent und führt zu einer fehlerhaften Antwort.

Der Artikel zeigt, dass bei der richtigen Lösung des Problems die Temperaturdifferenz der Kugeln nach der Übertragung der gleichen Wärmemenge auf sie gleich ist:

$$

wo $$ - die absolute Temperatur der Kugeln, $$ - die Änderungsrate des Wärmeausdehnungskoeffizienten des Materials der Kugeln bei Änderung seiner Temperatur.

Im Vergleich zum Ergebnis der herkömmlichen Lösung beträgt der Temperaturunterschied:

• Das entgegengesetzte Vorzeichen, da für die meisten Materialien der Wert $$ ist positiv, daher ist auch die gesamte rechte Seite der Gleichheit positiv, und $$ .
• Im absoluten Wert viel kleiner, da hier anstelle eines kleinen Wertes noch kleinere Werte erscheinen $$ und $$ .

Somit heben sich die beiden oben diskutierten Effekte fast vollständig auf, aber der zweite (Änderung der Wärmekapazität während des Zusammendrückens oder Zugens) ist etwas stärker als der erste (Wärmeausdehnung).

Anharmonizität interatomarer Kräfte

Die Autoren des Artikels führen eine ziemlich strenge Betrachtung des Problems durch, liefern jedoch leider keine klare Erklärung dafür, wie die fast vollständige Kompensation der beiden Effekte erfolgt, so dass ich mich selbst mit diesem Problem befassen musste.

Die Abbildung zeigt eine typische Abhängigkeit der potentiellen Energie der atomaren Wechselwirkung vom Abstand zwischen ihnen. Die auf die Atome wirkende Kraft ist auf eine Abnahme der potentiellen Energie gerichtet, daher stoßen sich Atome in kleinen Entfernungen stark ab und werden in großen Entfernungen schwach angezogen. In einiger Entfernung $$ potentielle Energie erreicht ein Minimum. Der Wunsch der Atome nach dieser energetisch vorteilhaftesten Entfernung ist der Grund für ihre Bindung an Moleküle, Flüssigkeiten und Feststoffe.


Nun wollen wir sehen, woher die Wärmeausdehnung der Materialien kommt. Bei chaotischer thermischer Bewegung ist der Abstand zwischen den Atomen nicht mehr genau gleich $$ und schwankt in der Nähe dieses Wertes. Die Bindung zwischen Atomen hat die Eigenschaft des Anharmonismus: Sie verhält sich wie eine asymmetrische Feder, die leichter zu dehnen als zu komprimieren ist. Infolgedessen wird die Bindung während der thermischen Bewegung die meiste Zeit gedehnt und nicht komprimiert, so dass der durchschnittliche Abstand $$ zwischen Atomen wird mehr als $$ . Mit zunehmender Temperatur verstärkt sich dieser Effekt, die Abstände zwischen Atomen nehmen zu und das Material dehnt sich aus.


Der Grund für die Wärmeausdehnung von Materialien: Während der thermischen Bewegung nimmt der durchschnittliche Abstand zwischen Atomen aufgrund der Anharmonizität interatomarer Wechselwirkungskräfte zu.

Was passiert, wenn das Material zusammengedrückt oder gedehnt wird, wie bei abgeflachten oder gedehnten Kugeln? Wenn ein Material komprimiert wird, verringert eine äußere Kraft den durchschnittlichen Abstand zwischen Atomen, und wenn er gedehnt wird, nimmt er zu.


Unter Kompression nimmt der Gleichgewichtsabstand zwischen den Atomen ab, während er unter Spannung zunimmt.

Jetzt sind wir bereit zu verstehen, wie sich die Kompression und Spannung eines Materials auf seine Wärmekapazität auswirkt. Stellen Sie sich vor, wir hätten das Material zusammengedrückt, so dass der Abstand zwischen den Atomen während der thermischen Bewegung jetzt in der Nähe der nach links verschobenen Gleichgewichtsposition schwingt. In diesem Fall ist der Anharmonismus nicht verschwunden, daher nimmt der durchschnittliche Abstand zwischen Atomen nach wie vor beim Erhitzen zu. Gleichzeitig werden wir uns wieder dem Minimum an potentieller Energie zuwenden, was bedeutet, dass die Energie des Materials weiter abnimmt! Dies erklärt die Abnahme der Wärmekapazität des Materials während der Kompression: Die Wärmeausdehnung führt zu einer geringfügigen zusätzlichen Abnahme der Energie interatomarer Wechselwirkungen, daher wird weniger Energie benötigt, um das Material zu erwärmen.



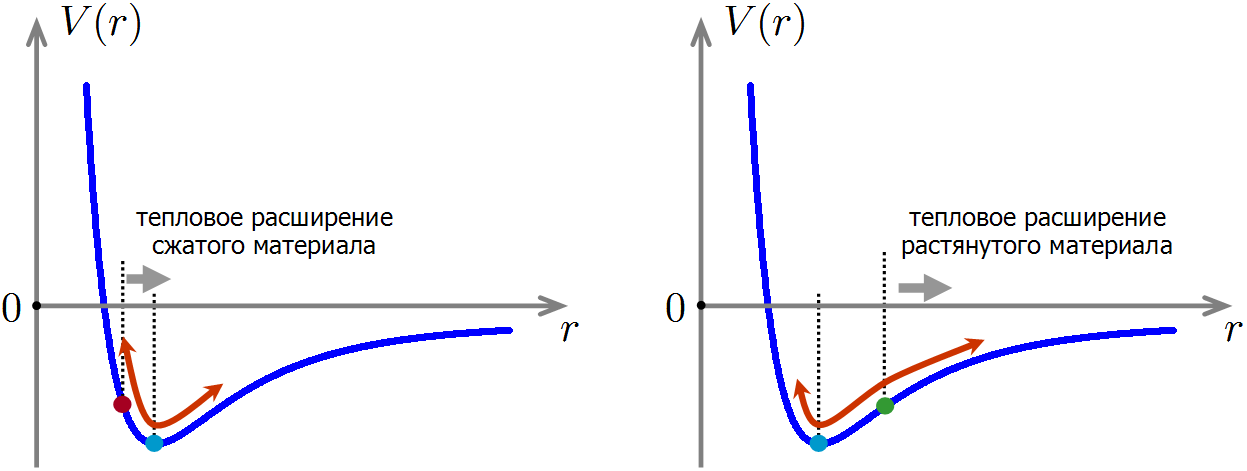
Wenn das Material gedehnt wird, ist die Situation umgekehrt: Mit der Wärmeausdehnung wächst die Wechselwirkungsenergie der Atome schneller als bei ungedehntem Material. Um das gestreckte Material auf die gleiche Temperatur zu erwärmen, ist daher etwas mehr Energie erforderlich als ohne Strecken, was bedeutet, dass die Wärmekapazität des gestreckten Materials höher ist.

Am Beispiel des Olympiadenproblems, das seit vielen Jahrzehnten fälschlicherweise gelöst wurde (und vielleicht auch weiterhin gelöst wird), sehen wir, dass die reale Physik manchmal unserer Intuition widerspricht. Daher ist es bei der Lösung von Problemen so wichtig, den mathematischen Apparat sorgfältig zu verwenden, ohne auf oberflächliches Denken beschränkt zu sein.

Nach dem Artikel :

Giacomo De Palma, Mattia C. Sormani, Gegenintuitive Wirkung der Schwerkraft auf die Wärmekapazität einer festen Kugel: Überprüfung eines bekannten Problems, American Journal of Physics 83, 723 (2015).
Öffentlicher Preprint des Artikels: arxiv.org/pdf/1502.01337