Vorwort zum ersten Teil
Das Modellieren von Dampfturbinen ist eine tägliche Aufgabe für Hunderte von Menschen in unserem Land. Anstelle des Wortmodells ist es üblich, ein Kostenmerkmal zu nennen . Die Verbrauchseigenschaften von Dampfturbinen werden zur Lösung von Problemen wie der Berechnung des spezifischen Verbrauchs von äquivalentem Brennstoff für Strom und Wärme verwendet, die von Wärmekraftwerken erzeugt werden. Optimierung des KWK; Planung und Wartung von Wärmekraftwerksmodi.
Ich habe eine neue Strömungscharakteristik einer Dampfturbine entwickelt - eine linearisierte Strömungscharakteristik einer Dampfturbine. Die entwickelte Strömungscharakteristik ist bequem und effektiv bei der Lösung dieser Probleme. Im Moment wird es jedoch nur in zwei wissenschaftlichen Arbeiten beschrieben:
- Optimierung des Betriebs von Wärmekraftwerken unter den Bedingungen des Großhandelsmarktes für elektrische Energie und Kapazität Russlands ;
- Berechnungsmethoden zur Bestimmung des spezifischen Verbrauchs an äquivalentem Brennstoff von Wärmekraftwerken für die zugeführte elektrische und thermische Energie im Modus der kombinierten Erzeugung .
Und jetzt möchte ich in meinem Blog:
1. Die Quelldaten
Die Anfangsdaten zum Aufbau einer linearisierten Strömungscharakteristik können sein
- tatsächliche Leistungswerte Q 0 , N, Q p , Q t, gemessen während des Betriebs der Dampfturbine,
- Nomogramme q t brutto aus der normativen und technischen Dokumentation.
Natürlich sind die tatsächlichen Momentanwerte von Q
0 , N, Q
p , Q
t ideale Quelldaten. Das Sammeln solcher Daten ist zeitaufwändig.
In Fällen, in denen die tatsächlichen Werte von Q 0 , N, Q p , Q t nicht verfügbar sind, können Sie Nomogramme q t brutto verarbeiten. Sie wurden wiederum auf der Grundlage von Messungen erhalten. Lesen Sie mehr über Turbinentests in VM Gornstein und andere Methoden zur Optimierung der Modi von Energiesystemen .
2. Der Algorithmus zum Erstellen einer linearisierten Strömungseigenschaft
Der Konstruktionsalgorithmus besteht aus drei Schritten.
- Übersetzung von Nomogrammen oder Messergebnissen in eine tabellarische Ansicht.
- Linearisierung der Strömungscharakteristik einer Dampfturbine.
- Bestimmung der Grenzen des Regelbereichs der Dampfturbine.
Wenn Sie mit Nomogrammen q t brutto arbeiten, ist der erste Schritt schnell. Diese Arbeit nennt man Digitalisierung . Das Digitalisieren von 9 Nomogrammen für das aktuelle Beispiel dauerte ungefähr 40 Minuten.
Der zweite und dritte Schritt erfordern die Verwendung mathematischer Pakete. Ich liebe und benutze MATLAB seit vielen Jahren. Mein Beispiel für die Konstruktion einer linearisierten Strömungscharakteristik ist darin enthalten. Ein Beispiel kann von der Verknüpfung heruntergeladen, ausgeführt und unabhängig die Methode zum Erstellen einer linearisierten Strömungscharakteristik ermittelt werden.
Die Strömungscharakteristik für die betreffende Turbine wurde für die folgenden festen Werte der Modusparameter erstellt:
- einstufiger Betrieb
- Mitteldruck Dampfdruck = 13 kgf / cm²,
- Niederdruckdampfdruck = 1 kgf / cm2.
Inhalt des Archivs Chuchueva-PT-80-lineare-Kennlinie.rar .
1) Nomogramme des spezifischen Verbrauchs qt brutto für die Stromerzeugung (markierte rote Punkte werden digitalisiert - auf die Tabelle übertragen):
- PT80_qt_Qm_eq_0_digit.png,
- PT80_qt_Qm_eq_100_digit.png,
- PT80_qt_Qm_eq_120_digit.png,
- PT80_qt_Qm_eq_140_digit.png,
- PT80_qt_Qm_eq_150_digit.png,
- PT80_qt_Qm_eq_20_digit.png,
- PT80_qt_Qm_eq_40_digit.png,
- PT80_qt_Qm_eq_60_digit.png,
- PT80_qt_Qm_eq_80_digit.png.
2) Das Ergebnis der Digitalisierung (jede CSV-Datei entspricht einer PNG-Datei):
- PT-80_Qm_eq_0.csv,
- PT-80_Qm_eq_100.csv,
- PT-80_Qm_eq_120.csv,
- PT-80_Qm_eq_140.csv,
- PT-80_Qm_eq_150.csv,
- PT-80_Qm_eq_20.csv,
- PT-80_Qm_eq_40.csv,
- PT-80_Qm_eq_60.csv,
- PT-80_Qm_eq_80.csv.
3) MATLAB-Skript mit Berechnungen und Grafiken:
- PT_80_linear_characteristic_curve.m
4) Das Ergebnis der Digitalisierung der Nomogramme und das Ergebnis der Erstellung einer linearisierten Strömungscharakteristik in Tabellenform:
- PT_80_linear_characteristic_curve.xlsx.
Schritt 1. Übersetzung von Nomogrammen oder Messergebnissen in eine tabellarische Ansicht
1. Quelldatenverarbeitung
Die Anfangsdaten für unser Beispiel sind Nomogramme q t brutto.
Um viele Nomogramme zu digitalisieren, benötigen Sie ein spezielles Werkzeug. Ich habe wiederholt eine Webanwendung für diese Zwecke verwendet. Die Anwendung ist einfach, bequem, bietet jedoch keine ausreichende Flexibilität, um den Prozess zu automatisieren. Ein Teil der Arbeit muss manuell erledigt werden.
In diesem Schritt ist es wichtig, die Extrempunkte der Nomogramme zu digitalisieren, die die Grenzen des Einstellbereichs der Dampfturbine definieren .
Die Aufgabe bestand darin, die Punkte der Entladungskennlinie in jeder PNG-Datei mit der Anwendung zu markieren, die resultierende CSV herunterzuladen und alle Daten in einer Tabelle zu sammeln. Das Ergebnis der Digitalisierung finden Sie in der Datei PT-80-lineare-Kennlinie.xlsx, Blatt „PT-80“, Tabelle „Eingabedaten“.
2. Bringen Sie Maßeinheiten zu Leistungseinheiten
Als nächstes berechnen wir auf dem Blatt "PT-80" die Werte von Q 0 gemäß der Formel
$$ Anzeige $$ \ Beginn {Gleichung} Q_0 = \ frac {q_T \ cdot N} {1000} + Q_P + Q_T \ qquad (1) \ Ende {Gleichung} $$ Anzeige $$
und wir bringen alle Anfangswerte auf MW. Die Berechnungen werden mit MS Excel durchgeführt.
Die resultierende Tabelle „Eingabedaten (Einheitsleistung)“ ist das Ergebnis des ersten Schritts des Algorithmus.
Schritt 2. Linearisierung der Dampfturbinenströmungscharakteristik
1. Testen von MATLAB
In diesem Schritt müssen Sie die MATLAB-Version mindestens 7.3 installieren und öffnen (dies ist eine alte Version, aktuelle Version 8.0). Öffnen Sie in MATLAB die Datei PT_80_linear_characteristic_curve.m, führen Sie sie aus und stellen Sie sicher, dass sie funktioniert. Alles funktioniert ordnungsgemäß, wenn nach den Ergebnissen der Ausführung des Skripts in der Befehlszeile die folgende Meldung angezeigt wird:
PT_80_linear_characteristic_curve.xlsx 1 : a(N) = 2.317, a(Q) = 0.621, a(Q) = 0.255, a0 = 33.874 = 0.006, (0.57
Wenn Sie Fehler haben, finden Sie selbst heraus, wie Sie diese beheben können.
2. Berechnungen
Alle Berechnungen sind in der Datei PT_80_linear_characteristic_curve.m implementiert. Betrachten wir es in Teilen.
1) Wir geben den Namen der Quelldatei, das Blatt und den Zellbereich an, der die im vorherigen Schritt erhaltene Tabelle „Quelldaten (Kapazitätseinheit)“ enthält.
XLSFileName = 'PT_80_linear_characteristic_curve.xlsx'; XLSSheetName = 'PT-80'; XLSRange = 'F3:I334';
2) Wir lesen die Quelldaten in MATLAB.
sourceData = xlsread(XLSFileName, XLSSheetName, XLSRange); N = sourceData(:,1); Qm = sourceData(:,2); Ql = sourceData(:,3); Q0 = sourceData(:,4); fprintf(' %s %1.0f \n', XLSFileName, toc);
Wir verwenden die Variable Qm für die durchschnittliche Strömungsgeschwindigkeit des Dampfes Qp, der Index m von der Mitte ist durchschnittlich; In ähnlicher Weise verwenden wir die Variable Ql für den Niederdruckdampfstrom Qn, der Index l von niedrig ist niedrig.
3) Definieren Sie die Koeffizienten α i .
Erinnern Sie sich an die allgemeine Formel für die Fließeigenschaften
$$ Anzeige $$ \ Anfang {Gleichung} Q_0 = f (N, Q_, Q_) \ qquad (2) \ Ende {Gleichung} $$ Anzeige $$
und geben Sie unabhängige (x_digit) und abhängige (y_digit) Variablen an.
x_digit = [N Qm Ql ones(size(N,1),1)];
Wenn Sie nicht verstehen, warum die x_digit-Matrix einen einzelnen Vektor (letzte Spalte) enthält, lesen Sie die linearen Regressionsmaterialien. Zum Thema Regressionsanalyse empfehle ich das Buch Draper N., Smith H. Angewandte Regressionsanalyse . New York: Wiley, In press, 1981. 693 p. (verfügbar in russischer Sprache).
Gleichung der linearisierten Strömungscharakteristik einer Dampfturbine
$$ Anzeige $$ \ begin {Gleichung} Q_0 = \ alpha_N \ cdot N + \ alpha_T \ cdot Q_P + \ alpha_T \ cdot Q_T + \ alpha_0 \ qquad (3) \ end {Gleichung} $$ Anzeige $$
ist ein multiples lineares Regressionsmodell. Die Koeffizienten α i werden unter Verwendung des "großen Nutzens der Zivilisation" - der Methode der kleinsten Quadrate - bestimmt. Unabhängig davon stelle ich fest, dass die Methode der kleinsten Quadrate 1795 von Gauß entwickelt wurde.
In MATLAB erfolgt dies in einer Zeile.
A = regress(y_digit, x_digit); fprintf(': a(N) = %4.3f, a(Q) = %4.3f, a(Q) = %4.3f, a0 = %4.3f\n',... A);
Variable A enthält die gewünschten Koeffizienten (siehe Meldung in der MATLAB-Befehlszeile).
Somit hat die erhaltene linearisierte Strömungscharakteristik der PT-80-Dampfturbine die Form
$$ Anzeige $$ \ begin {Gleichung} Q_0 = 2.317 \ cdot N + 0.621 \ cdot Q_ + 0.255 \ cdot Q_ + 33.874 \ qquad (4) \ end {Gleichung} $$ Anzeige $$
4) Wir schätzen den Linearisierungsfehler der erhaltenen Strömungscharakteristik.
y_model = x_digit * A; err = abs(y_model - y_digit) ./ y_digit; fprintf(' = %1.3f, (%4.2f%%)\n\n', mean(err), mean(err)*100);
Der Linearisierungsfehler beträgt 0,57% (siehe Meldung in der MATLAB-Befehlszeile).
Um die Bequemlichkeit der Verwendung der linearisierten Strömungscharakteristik einer Dampfturbine zu beurteilen, lösen wir das Problem der Berechnung der Hochdruckdampfströmungsrate Q 0 bei bekannten Lastwerten N, Q p , Q t .
Dann sei N = 82,3 MW, Q p = 55,5 MW, Q t = 62,4 MW
$$ Anzeige $$ \ begin {Gleichung} Q_0 = 2,317 \ cdot 82,3 + 0,621 \ cdot 55,5 + 0,255 \ cdot 62,4 + 33,874 = 274,9 \ qquad (5) \ end {Gleichung} $$ $$ anzeigen
Ich möchte Sie daran erinnern, dass der durchschnittliche Berechnungsfehler 0,57% beträgt.
Kehren wir zur Frage zurück, warum die linearisierte Strömungscharakteristik einer Dampfturbine grundsätzlich bequemer ist als Nomogramme des spezifischen Verbrauchs q t brutto für die Stromerzeugung. Lösen Sie zwei Probleme, um den grundlegenden Unterschied in der Praxis zu verstehen.
- Berechnen Sie Q 0 mit der angegebenen Genauigkeit anhand der Nomogramme und Ihrer Augen.
- Automatisieren Sie die Berechnung von Q 0 mithilfe von Nomogrammen.
Offensichtlich ist bei der ersten Aufgabe die Bestimmung von q Bruttowerten mit dem Auge mit groben Fehlern behaftet.
Die zweite Aufgabe ist umständlich zu automatisieren. Da die q q -Werte grob nichtlinear sind , ist für eine solche Automatisierung die Anzahl der digitalisierten Punkte zehnmal größer als im aktuellen Beispiel. Die Digitalisierung allein reicht nicht aus, es ist auch erforderlich, einen Algorithmus zum Interpolieren (Finden von Werten zwischen Punkten) nichtlinearer Bruttowerte zu implementieren.
Schritt 3. Festlegen der Grenzen des Einstellbereichs der Dampfturbine
1. Berechnungen
Um den Einstellbereich zu berechnen, verwenden wir ein anderes „Gut der Zivilisation“ - die konvexe Rumpfmethode, die konvexe Hülle.
In MATLAB wird dies wie folgt durchgeführt.
indexCH = convhull(N, Qm, Ql, 'simplify', true); index = unique(indexCH); regRange = [N(index) Qm(index) Ql(index)]; regRangeQ0 = [regRange ones(size(regRange,1),1)] * A; fprintf(' = %d\n\n', size(index,1));
Die Methode convhull () bestimmt die Grenzpunkte des Einstellbereichs, die durch die Werte der Variablen N, Qm, Ql gegeben sind. Die Variable indexCH enthält die Eckpunkte von Dreiecken, die mithilfe der Delaunay-Triangulation erstellt wurden. Die Variable regRange enthält die Grenzpunkte des Anpassungsbereichs. variabel regRangeQ0 - Hochdruckdampfdurchflussraten für die Grenzpunkte des Regelbereichs.
Das Berechnungsergebnis finden Sie in der Datei PT_80_linear_characteristic_curve.xlsx, Blatt „PT-80-Ergebnis“, Tabelle „Anpassungsbereichsgrenzen“.
Linearisierte Strömungscharakteristik aufgebaut. Es ist eine Formel (4) und 37 Punkte, die die Grenzen (Schale) des Einstellbereichs in der entsprechenden Tabelle definieren.
2. Überprüfung
Bei der Automatisierung der Berechnungsprozesse Q 0 muss geprüft werden, ob ein Punkt mit den Werten von N, Q p , Q t innerhalb oder außerhalb des Einstellbereichs liegt (der Modus ist technisch nicht realisierbar). In MATLAB kann dies wie folgt erfolgen.
Wir setzen die Werte von N, Q p , Q t , die wir überprüfen möchten.
n = 75; qm = 120; ql = 50;
Wir prüfen.
in1 = inpolygon(n, qm, regRange(:,1),regRange(:,2)); in2 = inpolygon(qm, ql, regRange(:,2),regRange(:,3)); in = in1 && in2; if in fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f \n', n, qm, ql); else fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f ( )\n', n, qm, ql); end
Die Überprüfung erfolgt in zwei Schritten:
- die Variable in1 gibt an, ob die Werte von N, Qp in die Projektion der Schale auf die Achse N, Qp gefallen sind;
- In ähnlicher Weise zeigt die Variable in2, ob die Werte von Qp, Qt innerhalb der Projektion der Schale auf die Achse von Qp, Qt liegen .
Wenn beide Variablen gleich 1 (wahr) sind, befindet sich der gewünschte Punkt innerhalb der Hülle, wodurch der Einstellbereich der Dampfturbine festgelegt wird.
Darstellung der erhaltenen linearisierten Strömungscharakteristik einer Dampfturbine
Die „großzügigsten Vorteile der Zivilisation“, die wir in Bezug auf die Darstellung der Berechnungsergebnisse erhalten haben.
Wir müssen zuerst sagen, dass der Raum, in dem wir die Graphen konstruieren, d. H. Der Raum mit den Achsen x - N, y - Q t , z - Q 0 , w - Q p , als Regimeraum bezeichnet wird (siehe Optimierung des Betriebs von Wärmekraftwerken unter den Bedingungen) Großhandelsmarkt für Strom und Kapazität von Russland
) Jeder Punkt dieses Raumes definiert eine bestimmte Betriebsart einer Dampfturbine. Modus kann sein
- technisch machbar, wenn sich der Punkt innerhalb der Schale befindet, der den Einstellbereich definiert,
- technisch nicht machbar, wenn der Punkt außerhalb dieser Schale liegt.
Wenn wir über den Kondensationsbetriebsmodus einer Dampfturbine sprechen (Q p = 0, Q t = 0), dann ist die linearisierte Strömungscharakteristik ein gerades Liniensegment . Wenn wir von einer T-Turbine sprechen, dann ist die linearisierte Strömungscharakteristik ein flaches Polygon im dreidimensionalen Regime-Raum mit den Achsen x-N, y-Qt, z-Q0, was leicht zu visualisieren ist. Für eine PT-Turbine ist die Visualisierung am schwierigsten, da die linearisierte Strömungscharakteristik einer solchen Turbine ein flaches Polygon im vierdimensionalen Raum ist (Erläuterungen und Beispiele finden Sie unter Optimierung des Betriebs eines Wärmekraftwerks auf dem russischen Strom- und Stromgroßhandelsmarkt, Abschnitt Linearisierung einer Turbinenströmungscharakteristik ).
1. Darstellung der erhaltenen linearisierten Strömungseigenschaften einer Dampfturbine
Lassen Sie uns die Werte der Tabelle "Eingabedaten (Leistungseinheit)" im Regime-Bereich erstellen.
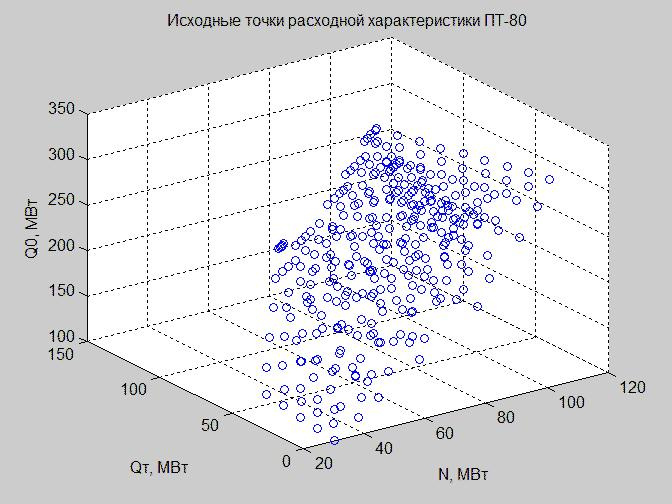
Abb. 3. Die Startpunkte der Strömungseigenschaften im Regime-Raum mit den Achsen x - N, y - Q t , z - Q 0
Da wir im vierdimensionalen Raum keine Abhängigkeit aufbauen können, haben wir noch kein solches Zivilisationsgut erreicht. Wir arbeiten mit den Werten von Q n wie folgt: Ausschließen (Abb. 3), Fixieren (Abb. 4) (siehe Code zum Erstellen von Graphen in MATLAB).
Wir legen den Wert von Q p = 40 MW fest und konstruieren die Startpunkte und die linearisierte Strömungscharakteristik.
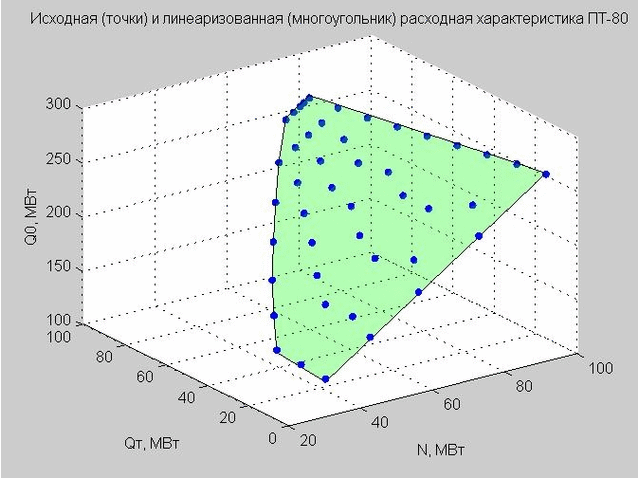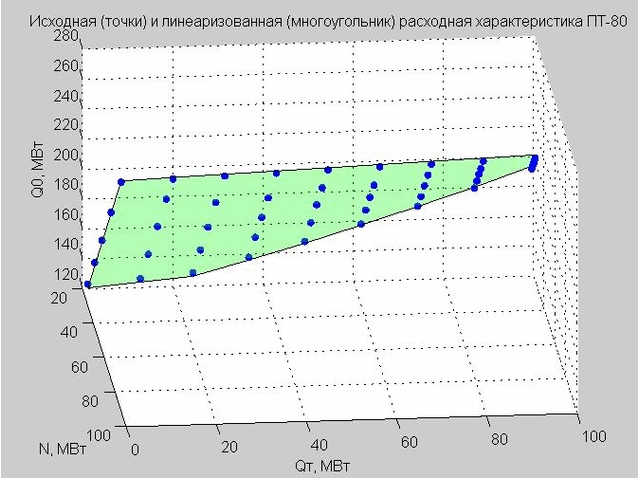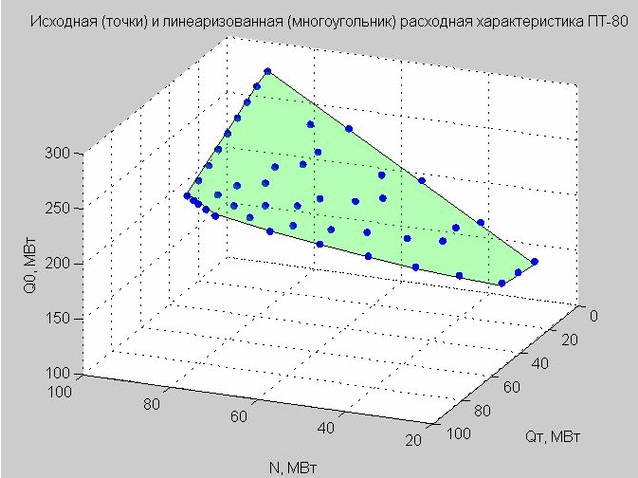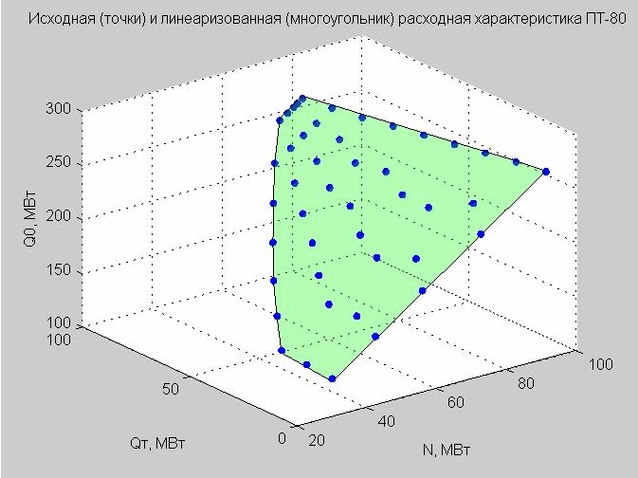
Abb. 4. Ausgangspunkte der Entladungscharakteristik (blaue Punkte), linearisierte Entladungscharakteristik (grünes flaches Polygon)
Kehren wir zu der Formel der linearisierten Durchflusskennlinie (4) zurück, die wir erhalten haben. Wenn wir Q p = 40 MW MW festlegen, hat die Formel die Form
$$ Anzeige $$ \ begin {Gleichung} Q_0 = 2.317 \ cdot N + 0.255 \ cdot Q_T + 58.714 \ qquad (6) \ end {Gleichung} $$ Anzeige $$
Dieses Modell definiert ein flaches Polygon im dreidimensionalen Raum mit den Achsen x - N, y - Q t , z - Q 0 in Analogie zu einer T-Turbine (wir sehen es in Abb. 4).
Vor vielen Jahren, als q Brutto-Nomogramme entwickelt wurden, wurde in der Phase der Analyse der Anfangsdaten ein grundlegender Fehler gemacht. Anstatt die Methode der kleinsten Quadrate anzuwenden und aus einem unbekannten Grund eine linearisierte Strömungscharakteristik einer Dampfturbine zu konstruieren, führten sie eine primitive Berechnung durch:
$$ Anzeige $$ \ Anfang {Gleichung} Q_0 (N) = Q_ = Q_0 - Q_ - Q_ \ qquad (7) \ Ende {Gleichung} $$ Anzeige $$
Subtrahiert von der Durchflussrate des Hochdruckdampfes Q 0 die Durchflussrate der Dämpfe Q t , Q p und schreibt die resultierende Differenz Q 0 (N) = Q e der Stromerzeugung zu. Der erhaltene Wert Q 0 (N) = Q e wurde durch N geteilt und in kcal / kW · h umgerechnet, nachdem ein spezifischer Verbrauch q t brutto erhalten worden war. Diese Berechnung entspricht nicht den Gesetzen der Thermodynamik.
Liebe Leser, vielleicht kennen Sie den unbekannten Grund? Teile es!
2. Darstellung des Einstellbereichs der Dampfturbine
Lassen Sie uns die Hülle des Einstellbereichs im Regime-Raum sehen. Die Ausgangspunkte für seine Konstruktion sind in Abb. 1 dargestellt. 5. Dies sind die gleichen Punkte, die wir in Abb. 5 sehen. In 3 ist jedoch der Parameter Q 0 jetzt ausgeschlossen.

Abb. 5. Die Startpunkte der Strömungseigenschaften im Regime-Raum mit den Achsen x - N, y - Q p , z - Q t
Viele Punkte in Abb. 5 ist konvex. Mit der Funktion converxhull () haben wir die Punkte definiert, die die äußere Hülle dieser Menge definieren.
Die Delaunay-Triangulation (eine Reihe verbundener Dreiecke) ermöglicht es uns, die Schale des Einstellbereichs zu konstruieren. Die Eckpunkte der Dreiecke sind die Grenzwerte des Einstellbereichs der betrachteten Dampfturbine PT-80.
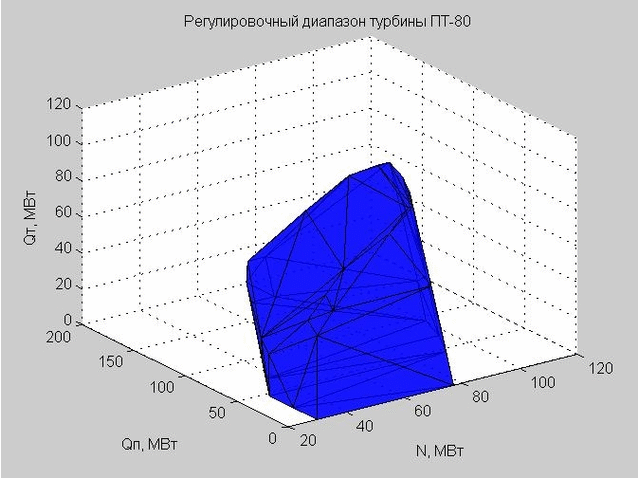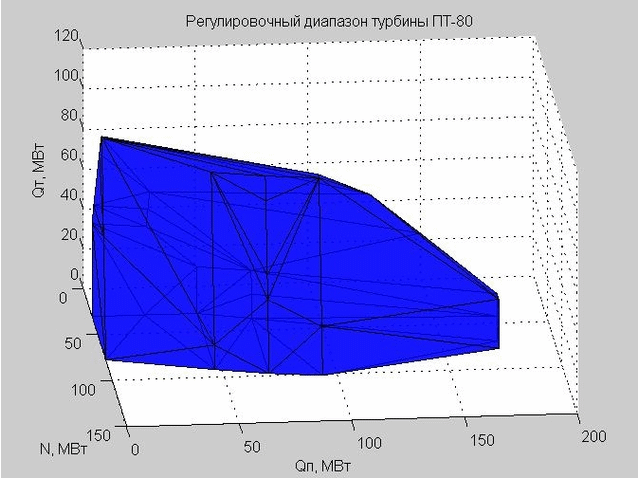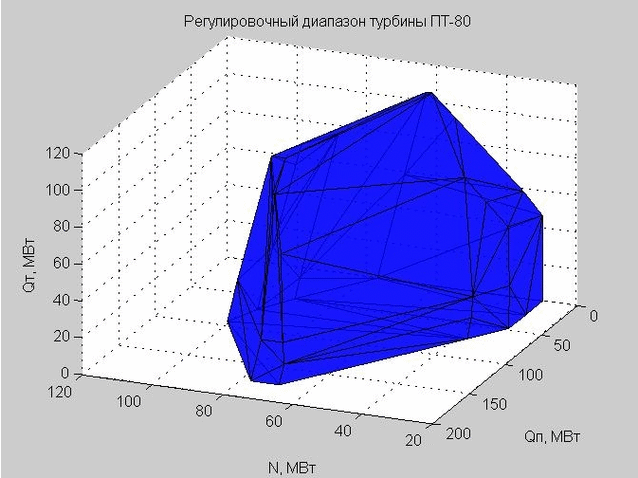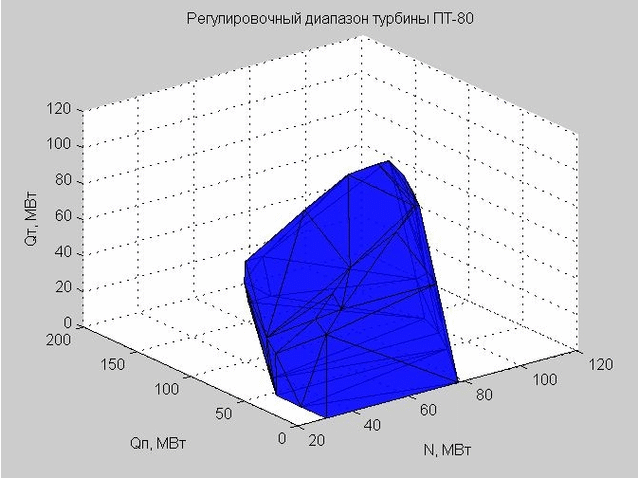
Abb. 6. Die Schale des Einstellbereichs, dargestellt durch viele Dreiecke
Als wir einen bestimmten Punkt überprüft haben, um in den Einstellbereich zu gelangen, haben wir überprüft, ob dieser Punkt innerhalb oder außerhalb der resultierenden Schale liegt.
Alle oben dargestellten Diagramme werden mit MATLAB-Tools erstellt (siehe PT_80_linear_characteristic_curve.m).
Vielversprechende Aufgaben im Zusammenhang mit der Analyse des Betriebs einer Dampfturbine anhand einer linearisierten Strömungscharakteristik
Wenn Sie ein Diplom oder eine Dissertation machen, kann ich Ihnen verschiedene Aufgaben anbieten, deren wissenschaftliche Neuheit Sie der ganzen Welt leicht beweisen können. Darüber hinaus leisten Sie hervorragende und nützliche Arbeit.
Aufgabe 1
Zeigen Sie, wie sich das flache Polygon ändert, wenn sich der Niederdruckdampfdruck Q t ändert.
Aufgabe 2
Zeigen Sie, wie sich das flache Polygon ändert, wenn sich der Druck im Kondensator ändert.
Aufgabe 3
Überprüfen Sie, ob die Koeffizienten der linearisierten Strömungscharakteristik als Funktionen zusätzlicher Parameter des Regimes dargestellt werden können, nämlich:
$$ Anzeige $$ \ begin {Gleichung} \ alpha_N = f (p_ {0}, ...); \\ \ alpha_P = f (p_ {P}, ...); \\ \ alpha_T = f (p_ {T}, ...); \\ \ alpha_0 = f (p_ {2}, ...). \ end {Gleichung} $$ Anzeige $$
Hier sind p 0 - Hochdruckdampfdruck, p p - Mitteldruckdampfdruck, p t - Niederdruckdampfdruck, p 2 - Abgasdampfdruck im Kondensator, alle Einheiten sind kgf / cm2.
Begründen Sie das Ergebnis.
Referenzen
Chuchueva I.A., Inkina N.E. Optimierung des KWK unter den Bedingungen des Großhandelsmarktes für Strom und Kapazität Russlands // Wissenschaft und Bildung: Wissenschaftliche Ausgabe der MSTU. N.E. Bauman. 2015. Nr. 8. S. 195-238.
Chuchueva I.A. Berechnungsmethoden zur Bestimmung des spezifischen Verbrauchs von äquivalentem Brennstoff von Wärmekraftwerken für die zugeführte elektrische und thermische Energie im Modus der kombinierten Erzeugung // Wissenschaft und Bildung: Wissenschaftliche Veröffentlichung der MSTU. N.E. Bauman. 2016. Nr. 2. S. 135-165.
Linearisierte Strömungscharakteristik einer Dampfturbine.