Masse, Energie, Impuls und das Naturschutzgesetz

Viele obskure Eigenschaften der Welt hängen mit der Natur von Masse und Energie (sowie dem Impuls) zusammen. Wir alle haben diese Worte gehört und viele von uns haben eine vage Vorstellung von ihrer Bedeutung. Natürlich gibt es viele Bedeutungen der Wörter "Masse" und "Energie" in Englisch und anderen Sprachen. Leider stimmt keiner von ihnen mit denen überein, die Physiker im Sinn haben. Versuchen Sie, diese Bedeutungen von Wörtern beiseite zu legen und mit exakten physikalischen Konzepten zu arbeiten - sonst werden Sie völlig verwirrt sein.

Es sollte beachtet werden, dass man sich nicht an ein anderes beliebtes Paar erinnern sollte, "Substanz und Energie" mit dem Ausdruck "Masse und Energie". Viele Leute erwähnen den letzten Satz, als ob Materie und Energie zwei Seiten derselben Medaille sind. Aber das ist nicht so. Materie und Energie fallen in verschiedene Kategorien wie Äpfel und Orang-Utans. Eine Substanz, egal wie sie definiert wird, ist eine Klasse von Objekten, die im Universum existieren, und Masse und Energie sind keine Objekte, sondern die Eigenschaften, die diese Objekte besitzen. Masse und Energie sind tief miteinander verflochten und verdienen eine allgemeine Erklärung.

Um Masse und Energie zu verstehen, müssen Sie ihnen Schwung verleihen und die Unterschiede und Beziehungen dieser Größen diskutieren.

Energie

Das Wort "Energie" hat viele Bedeutungen. Wenn wir krank werden, sagen wir, dass wir keine Energie mehr haben, was Kraft und Motivation betrifft. Wenn wir sagen, dass jemand voller Energie ist, meinen wir seine hohe Aktivität. Wir beschweren uns über steigende Energiepreise in Bezug auf Kraftstoff. Wir sprechen von spiritueller Energie als etwas Unermesslichem, aber Wichtigem, vielleicht einer Form von Charisma. Und all diese Konzepte überschneiden sich, daher wählen wir ein Wort, um sie zu beschreiben. Aber in der Physik ist Energie eine ganz andere Sache. Aus physikalischer Sicht wird eine dieser Definitionen fälschlicherweise mit der physikalischen verwechselt. In der Physik muss man sich an einen physikalischen Begriff halten, um nicht die falschen Antworten zu erhalten und nicht völlig verwirrt zu werden.

Leider ist das Konzept der „Energie“ in der Physik sehr schwer zu beschreiben, wie es Wörterbücher tun - mit einem kurzen aussagekräftigen Satz. Aber denken Sie nicht schlecht - das Ganze ist die Unvollkommenheit der natürlichen Sprache und nicht, dass das Konzept der Energie in der Physik vage ist. In jedem gegebenen physikalischen System ist völlig klar, was seine Energie ist, sowohl im Sinne seiner experimentellen Messung als auch im Sinne von Berechnungen (wenn es Gleichungen gibt, die das System beschreiben).

Einer der Gründe, warum Energie so schwer zu beschreiben ist, ist, dass sie viele Formen annehmen kann und nicht alle leicht zu verstehen sind. Hier sind drei gängige Sorten:

1. Energie kann in der Masse eines Objekts eingeschlossen sein. Hier nenne ich diese Option "Massenenergie" (dank der bekannten Gleichung E = mc ² bindet sich ^die Energie an die Masse. Sie wird auch "Ruheenergie" genannt, da dies die Energie eines ruhenden Objekts ist, dh ohne Bewegung).

2. Zweitens ist Energie mit der Bewegung eines Objekts verbunden. Hier nenne ich es "Bewegungsenergie", und der Fachbegriff dafür ist kinetische Energie. Diese Option ist intuitiv leicht zu erfassen, da sich schnell bewegende Objekte mehr Energie haben als sich langsam bewegende. Außerdem hat ein schweres Objekt mehr Bewegungsenergie als ein leichtes Objekt, das sich mit derselben Geschwindigkeit bewegt.

3. Energie kann in der Beziehung von Objekten gespeichert werden (und wird normalerweise als "Potential" bezeichnet). Es wird in einer gedehnten Quelle gespeichert, im Wasser hinter dem Damm, in der Gravitationswechselwirkung von Erde und Sonne, in der Wechselwirkung von Atomen im Molekül. Es gibt viele Möglichkeiten, Energie zu speichern. Es klingt vage, aber die Sprache ist schuld. In jedem dieser Fälle gibt es genaue Formeln, die die im System gespeicherte Energie beschreiben und genau definierte Methoden zur Messung.

Die dritte Art von Energie hängt mit dem zusammen, was ich Interaktionsenergie nennen werde, und dies ist das verwirrendste Konzept von allen. Im Gegensatz zur Energie der Masse und der Bewegungsenergie, die immer größer oder gleich Null sind, kann die Energie der Wechselwirkungen positiv und negativ sein. Bisher werde ich dieses Thema verlassen, aber wir werden darauf zurückkommen.

Energie ist eine besondere Größe, die für die Physik von großer Bedeutung ist. Der Grund für diese Bedeutung ist, dass es "erhalten" bleibt. Was bedeutet das?

Wenn Sie die Beobachtung mit einem Objekt oder einer Reihe von Objekten beginnen - wir nennen sie ein „System von Objekten“ -, die zu Beginn eine bestimmte Energiemenge besitzen (vergessen Sie nicht, alle Energien zu berechnen - Massen, Bewegungen, gespeicherte Energie aller Art usw.) und dann Teile des Systems interagieren nur miteinander und mit nichts anderem. Am Ende der Beobachtung ist die Gesamtenergiemenge dieser Objekte dieselbe wie zu Beginn. Die Gesamtenergie des Systems wird eingespart - die Gesamtmenge ändert sich nicht. Es kann seine Form ändern, aber wenn Sie alle Sorten im Auge behalten, ist es am Ende genauso viel wie am Anfang.

Diese Regel funktioniert auch dann, wenn einige Objekte verschwinden und anderen weichen, z. B. wenn ein Partikel im System in zwei andere zerfällt, die in das System übergehen .

Warum wird Energie gespart? Aufgrund des mathematischen Prinzips korreliert die Tatsache, dass sich die Naturgesetze im Laufe der Zeit nicht ändern, mit der Existenz einer konservierten Größe, die wir per Definition "Energie" nennen.

Die berühmteste und allgemeinste Definition dieses Prinzips verdanken wir Emmy Noether , einem der größten mathematischen Physiker des vorigen Jahrhunderts, einem Zeitgenossen von Einstein. Einige Mitglieder der physischen und mathematischen Gemeinschaft behandelten sie mit tiefem Respekt , aber zu dieser Zeit litt sie in ihrer Heimat Deutschland unter Diskriminierung aufgrund des Geschlechts und der Nationalität (dort blockierten sie Versuche, ihr den Titel einer Professorin in Göttingen zuzuweisen, und von dort musste sie fliehen die Nazis kamen an die Macht). Nach ihrer Auswanderung in die USA starb sie nach nur zweijähriger Lehrtätigkeit am Brin-Mar College (das bis heute nur Frauen für die Ausbildung akzeptiert) an Krebs.

Das berühmte Noether-Theorem (eigentlich sind dies zwei eng verwandte Theoreme) sagt uns, dass, wenn die Naturgesetze symmetrisch sind - in unserem Fall bedeutet dies, dass die Naturgesetze zu jedem Zeitpunkt gleich sind - dies die Erhaltung einer bestimmten Menge impliziert - in unserem Fall Energie .

Darüber hinaus sagt uns der Satz genau, wie groß die Größe ist - welche unterschiedlichen Energieformen für ein bestimmtes System von Objekten erforderlich sind, um Gesamtenergie zu erhalten. Deshalb wissen Physiker immer genau, was Energie ist und warum es einfacher ist, Gleichungen zu erhalten, als sie in Worten zu definieren.

Impuls

Die Situation mit dem Impuls ist ungefähr die gleiche wie mit der Energie. Die Naturgesetze sind überall gleich. Grob gesagt geben die Experimente die gleichen Antworten, egal ob Sie sie nördlich oder südlich von hier, westlich oder östlich, auf einem Gebäude oder in einem tiefen Schacht verbringen. Wähle eine beliebige Richtung im Raum. Dann bleibt laut Noether der Impuls entlang dieser Richtung erhalten. Da es im Raum drei Dimensionen gibt, ist es möglich, sich in drei verschiedene unabhängige Richtungen zu bewegen, und es gibt drei unabhängige Erhaltungsgesetze. Sie können drei beliebige Richtungen wählen, sofern diese unterschiedlich sind. Beispielsweise können Sie Impulse in Nord-Süd-, West-Ost- und Auf-Ab-Richtung als die drei Erhaltungsgesetze auswählen. Oder Sie können drei weitere auswählen - in Richtung zur und von der Sonne, entlang der Erdumlaufbahn in beide Richtungen und auf und ab in Bezug auf die Ebene des Sonnensystems. Ihre Wahl spielt keine Rolle, da der Impuls in jeder Richtung gespeichert wird.

Die einfachste Form des Impulses entsteht durch die einfache Bewegung von Objekten, und dies kann man sich intuitiv vorstellen: Wenn sich ein Objekt in eine bestimmte Richtung bewegt, hat es einen Impuls in diese Richtung, und je schneller es sich bewegt, desto größer ist dieser Impuls. Und ein schwereres Objekt hat einen größeren Impuls als ein leichtes, wenn es sich mit der gleichen Geschwindigkeit bewegt.

Eine der interessanten Konsequenzen dieser Erhaltung: Wenn Sie ein bewegungsloses Objektsystem haben (dh das System als Ganzes bewegt sich nicht, wenn Sie alle Bewegungen seiner konstituierenden Objekte mitteln), bleibt es bewegungslos, es sei denn, es wird von außen bewegt Auswirkungen. Der Grund ist, dass in einem festen System der Gesamtimpuls Null ist, und da der Impuls beibehalten wird, bleibt er für immer Null, es sei denn, etwas greift von außerhalb des Systems ein.

Masse und ihre Beziehung zu Energie und Impuls

Wenden wir uns nun der Masse zu

Leider ist viel Verwirrung mit Masse verbunden - nach der Veröffentlichung von Einsteins Arbeit zur Relativitätstheorie für einige Zeit gab es zwei Konzepte von Masse. Und nur einer von ihnen (derjenige, bei dem Einstein selbst aufgehört hat und der manchmal als "invariante Masse" oder "Ruhemasse" bezeichnet wird, um ihn von dem bereits archaischen Begriff "relativistische Masse" zu unterscheiden) wird in der Teilchenphysik noch verwendet. In einem separaten Artikel werde ich dies näher erläutern.


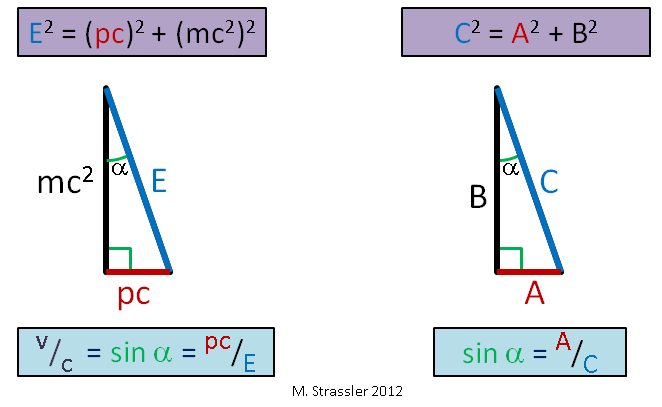Abb. 1

Mit Masse m, die ich in Artikeln verwende, ist die Masse gemeint, die Energie und Impuls direkt bindet. Für ein Objekt, das sich ohne den Einfluss äußerer Kräfte bewegt (ohne signifikante Wechselwirkung mit anderen Objekten), schlug Einstein vor (und dies wurde durch Experimente bestätigt), dass seine Energie E, sein Impuls p und seine Masse m die einfache pythagoreische Gleichheit erfüllen:

$$ $$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2 \ qquad (Gleichung Nr. 1)$$

Erinnern Sie sich an die alten Pythagoras, die behaupteten, dass für ein rechtwinkliges Dreieck mit den Seiten A und B und der Hypotenuse C die Gleichheit gilt $$$C ^ 2 = A ^ 2 + B ^ 2$ ? Dies ist eine Verbindung des gleichen Typs - siehe Abb. 1. Bei uns ist c eine konstante Geschwindigkeit, die, wie wir sehen werden, als universelle Geschwindigkeitsbegrenzung dient. Wir werden auch sehen, warum es die "Lichtgeschwindigkeit" genannt wird.

Nach Einsteins Gleichungen ist die Geschwindigkeit eines Objekts geteilt durch die Geschwindigkeitsbegrenzung c nur das Verhältnis von pc zu E:

$$ $$v / c = (p c) / E \ qquad (Gleichung # 2)$$

Das heißt, das Verhältnis des horizontalen Beins zur Hypotenuse. Sie ist auch gleich dem Sinus des Winkels α in Fig. 1. 1. Also hier, Bürger. Und da die Beine eines rechtwinkligen Dreiecks immer kürzer als die Hypotenuse sind (der Sinus eines beliebigen Winkels ist immer kleiner oder gleich 1), darf die Geschwindigkeit eines Objekts s, die universelle Geschwindigkeitsbegrenzung, nicht überschreiten. Mit zunehmender Geschwindigkeit eines Objekts mit fester Masse werden p und E sehr groß (Abb. 2), aber E ist immer größer als pc, also ist v immer kleiner als c!


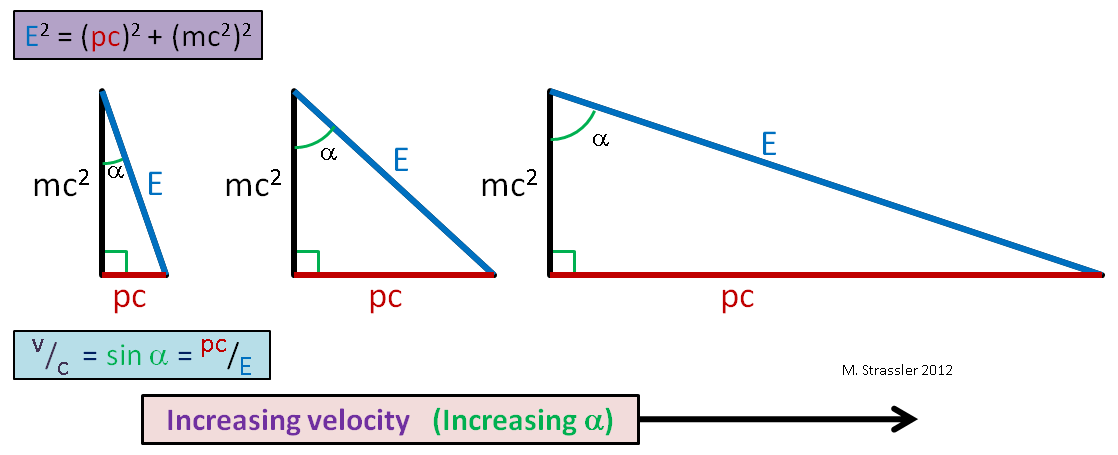Abb. 2

Beachten Sie nun, dass, wenn sich das Objekt nicht bewegt, sein Impuls p gleich Null ist und sich das Verhältnis in Gleichung 1 auf Folgendes verringert:

$$ $$E ^ 2 = (mc ^ 2) ^ 2, \ quad oder \ quad E = mc ^ 2$$

Einsteins berühmte Formel, das Verhältnis von Masse zu einer festen Energiemenge (was ich Massenenergie nenne), ist einfach eine Aussage, die der Tatsache entspricht, dass ein Dreieck in eine vertikale Linie ausartet, wie in Abb. 3 auf der linken Seite wird seine Hypotenuse gleich lang wie das vertikale Bein. Gleichzeitig bedeutet dies nicht, dass Energie immer gleich Masse mal Quadrat s ist. Dies funktioniert nur für ein ruhendes Objekt ohne Impuls.


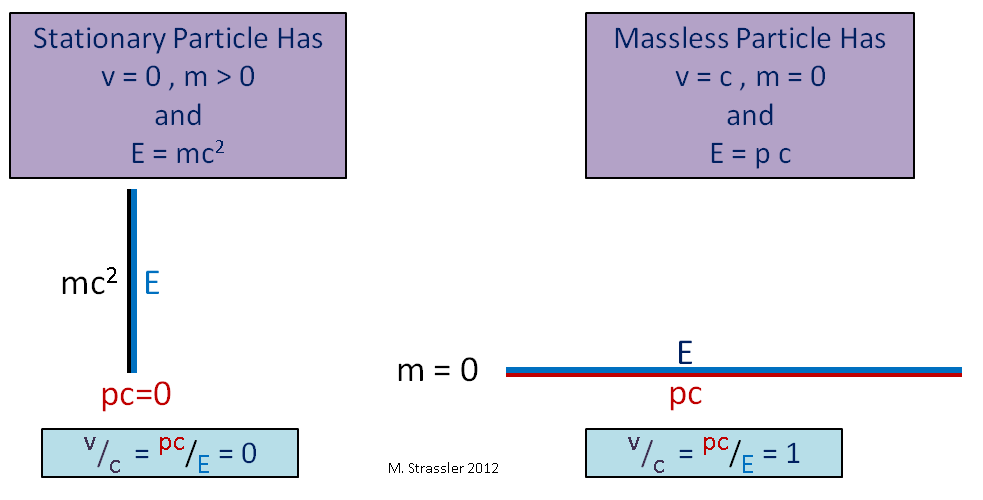Abb. 3

Eine weitere interessante Beobachtung: Für ein masseloses Teilchen ist der vertikale Schenkel des Dreiecks Null, und die Hypotenuse und der horizontale Schenkel sind dieselben wie in Abb. 3. In diesem Fall ist E pc, was bedeutet, dass v / c = 1 oder v = c ist. Es ist ersichtlich, dass sich ein masseloses Teilchen (zum Beispiel ein Photon, ein Lichtteilchen) unvermeidlich mit einer Geschwindigkeit von c bewegt. Daher ist die Lichtgeschwindigkeit dieselbe wie die universelle Geschwindigkeitsbegrenzung s.

Wenn wir dagegen ein Teilchen mit Masse nehmen, wie in Abb. 4, es spielt keine Rolle, wie groß Sie den Impuls und die Energie machen, E wird immer etwas mehr als p * c sein, also wird die Geschwindigkeit immer kleiner als s sein. Masselose Partikel müssen sich mit maximaler Geschwindigkeit fortbewegen. Die Geschwindigkeit massereicher Partikel sollte geringer sein.


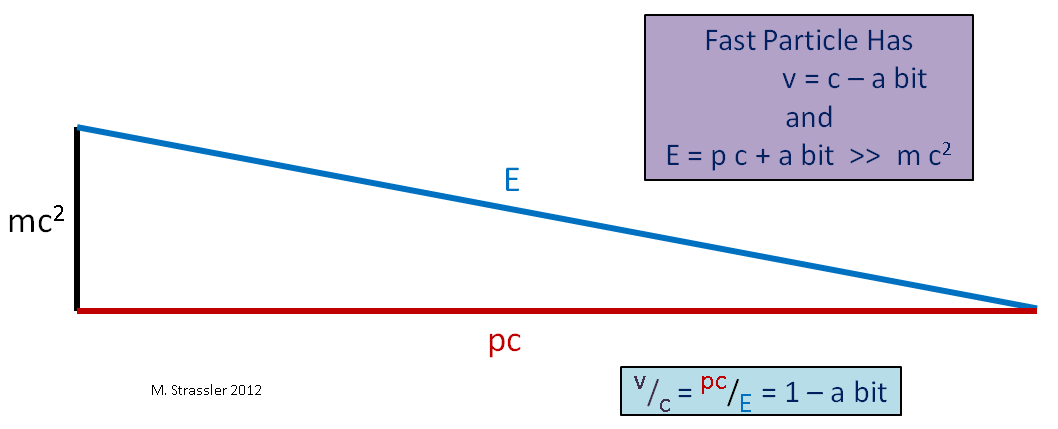Abb. 4. Hier bedeutet ">>" "viel mehr"

Stellen Sie sich einen anderen Grenzfall vor, ein sich langsam bewegendes (im Vergleich zur Lichtgeschwindigkeit) massives Objekt wie ein Auto. Da seine Geschwindigkeit v viel kleiner als c ist, ist sein Impuls p mal c viel kleiner als E, und wie aus Fig. 1 ersichtlich ist. 5, E wird etwas mehr als mc ^{2 sein} . Daher ist die Bewegungsenergie eines langsamen Objekts E - mc ² viel geringer als die Energie seiner Masse mc ² , und für ein schnelles Objekt kann die Bewegungsenergie beliebig groß gemacht werden, wie wir in Abb. 4.

Ein subtiler Punkt: Impuls ist nicht nur eine Zahl, sondern auch ein Vektor. Er hat Größe und Richtung. Es ist auf die Bewegung des Teilchens gerichtet. Wenn ich p schreibe, gebe ich nur den Wert an. In vielen Fällen ist es notwendig, die Richtung des Impulses zu verfolgen, obwohl dies in Gleichung Nr. 1, die den Impuls auf Energie und Masse bezieht, nicht erforderlich ist.


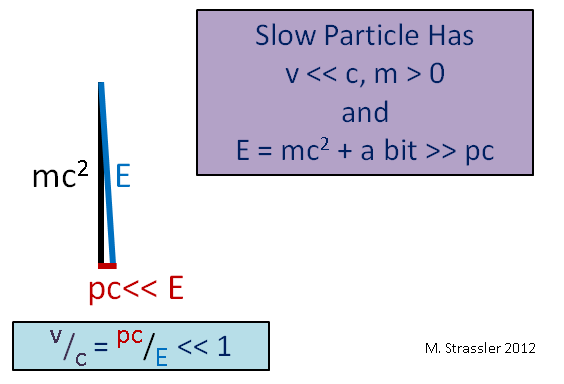Abb. 5

Ein weiterer subtiler Punkt: Ich habe Dreiecke und einfache Trigonometrie verwendet, da dies jedem aus der Schule bekannt ist. Experten müssen vorsichtiger sein - Sie können Einsteins Gleichungen mit hyperbolischen Funktionen richtig verstehen, die normalerweise von Amateuren nicht gefunden werden, aber äußerst wichtig sind, um die Struktur der Theorie zu verstehen und Dinge wie Geschwindigkeitsaddition, Distanzkompression usw. verständlicher zu machen. Menschen, die nicht vorgeben, Experten zu sein, können dies ignorieren.

Aber ist die Geschwindigkeit relativ? ..

Wenn Sie den Text sorgfältig lesen, kann Sie bereits etwas überraschen. Sie wissen, dass die Geschwindigkeit eines Partikels - oder etwas, das sich langsamer als Licht bewegt - vom Standpunkt abhängt.

Wenn Sie zu Hause sitzen und ein Buch lesen, werden Sie sagen, dass die Geschwindigkeit des Buches Null ist (und es wirklich relativ zu Ihnen ruht), daher hat es keinen Impuls und keine Bewegungsenergie, nur Energie der Masse. Aber wenn ich auf dem Mond stehen würde, würde ich dich daran erinnern, dass sich die Erde dreht, also fesselt dich diese Rotation und bewegt dich relativ zu mir mit einer Geschwindigkeit von Hunderten von Stundenkilometern. Sie und Ihr Buch hätten also aus meiner Sicht den Impuls.

Wer hat recht?

Die Relativitätsvariante nach Galileo - das erste Relativitätsprinzip - besagt, dass wir beide Recht haben. Einsteins Relativitätsvariante stimmt mit Galileos Standpunkt überein, dass beide richtig sind, nimmt jedoch wichtige Anpassungen daran vor, wie Galileos Anhänger die Energie, den Impuls und die Masse des Buches anzeigen würden, indem sie diese Größen in die pythagoreische Beziehung von Gleichung Nr. 1 einordnen.

Aber wenn alles in Ordnung ist, welches E und welches p muss ich im Verhältnis von Energie / Impuls / Masse einsetzen, $$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2$ ? Ersetzen Sie E und p, gemessen durch Lesen des Buches, d. H. E = mc ² und p = 0? Oder ersetzen Sie E und p, die das Buch aus meiner Sicht hat, wenn Sie sich mit der Erde bewegen?

Die Antwort auf diese Frage enthält die gesamte Essenz von Einsteins Gleichung Nr. 1. Jeder Beobachter misst unterschiedliche Werte von E und p für das Buch, je nachdem, wie schnell sich das Buch relativ dazu bewegt. Aber für alle Beobachter die Gleichung $$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2$ wird wahr sein!

Die Magie! Tatsächlich ist Genie eine Idee, die 1905 aufkam, wie der von Newton und seinen Anhängern vorgeschlagene Satz von Gleichungen durch einen neuen erstaunlichen Satz von Gleichungen ersetzt werden kann, der immer noch mit allen vorherigen Experimenten übereinstimmt, sich jedoch als genauere Darstellung der Realität herausstellte. Es ist schwer vorstellbar, wie sehr es notwendig war, die Denkweise zu ändern, um darüber nachzudenken, bis Sie herausgefunden haben, wie viel bei der Bildung der neuen Theorie alles schief gehen könnte und wie viele andere Gleichungen, die Widersprüche zur Mathematik oder zu früheren Experimenten enthalten, Sie können Es wäre zu bieten (und die Leute boten sie an). Zum Beispiel kommt die Arbeit von unerfahrenen Physikern ständig zu mir und versucht, Einsteins Gleichungen zu „reparieren“, aber ich habe noch nie gesehen, dass einer von ihnen seine Gleichungen auf interne Konsistenz überprüft. Dies ist eine sehr schwierige Aufgabe und der Grund für das Scheitern der meisten Theorien.

Aber wie können dann Energie und Dynamik erhalten werden?

Warten Sie eine Minute, sagen Sie, wenn Ihr Kopf bereit ist, alles um Sie herum mit Ihrem Gehirn zu explodieren und zu bespritzen (ich erinnere mich an diese Empfindung selbst), aber Energie und Schwung müssen erhalten bleiben! Wie können verschiedene Beobachter nicht mit dem übereinstimmen, was sie sind?

Es gibt noch mehr Magie, die übrigens vor Einstein war. Glauben Sie mir, das Universum ist ein sehr, sehr kluger Buchhalter, und obwohl sich verschiedene Beobachter nicht auf die in einem Objekt oder Objektsystem verfügbare Energie einigen, sind sich alle einig, dass sich diese Energie nicht mit der Zeit ändert. Gleiches gilt für die Dynamik.

Aber die Masse unterscheidet sich sehr von Energie und Impuls. Erstens bleibt die Masse nicht erhalten. In der Natur gibt es viele Prozesse, die die Gesamtmasse eines Systems verändern: Beispielsweise kann ein massives Higgs-Teilchen in zwei masselose Photonen zerfallen. Mit Masse ist keine Symmetrie verbunden, und deshalb hat Noether kein Erhaltungsgesetz für uns. Zweitens stimmen im Gegensatz zu Energie und Impuls, deren Werte vom Beobachter abhängen (insbesondere von seiner Geschwindigkeit in Bezug auf die gemessenen Objekte), alle Beobachter mit der Masse m des Objekts überein. Und das ist überhaupt nicht offensichtlich und geschieht, weil die Einstein-Gleichungen furchtbar schlau funktionieren.

Was haben wir also?

Im Moment haben wir einige auf den ersten Blick widersprüchliche Kenntnisse. Wir wissen das:

• Die Energie und der Impuls eines isolierten physikalischen Systems bleiben aus Sicht eines Beobachters erhalten (die Gesamtenergie und der Gesamtimpuls eines isolierten Systems ändern sich nicht mit der Zeit).
• Verschiedene Beobachter, die sich relativ zueinander bewegen, bewerten die Werte der Energie und des Impulses des Systems unterschiedlich!
• Die Summe der Massen der Objekte, aus denen das System besteht, wird nicht gespeichert, sondern kann sich ändern.
• Alle Beobachter stimmen jedoch der Masse des Objekts zu.

Zu dieser Liste müssen zwei weitere Fakten und zwei Schlussfolgerungen hinzugefügt werden:

Die Masse des physischen Systems von Objekten ist nicht gleich der Summe der Massen der Objekte, aus denen dieses System besteht.

Stattdessen wird die Masse des physikalischen Systems, über die sich alle Beobachter einig sind, durch seine Energie und seinen Impuls bestimmt und erfüllt seine Version von Gleichung Nr. 1:

$$ $$(E_{system})^2 = (p_{system} c)^2 + (m_{system} c^2)^2 \qquad ( №1')$$

Es stellt sich heraus, dass ein zusätzliches Erhaltungsgesetz nicht erforderlich ist und dass, obwohl die Summe der Massen der Objekte, aus denen das System besteht, nicht erhalten bleibt, die Masse des Systems erhalten bleibt, da sie durch Gleichung Nr. 1 'mit der Energie und dem Impuls des gespeicherten Systems verbunden ist.

Die Masse des Objektsystems ist der einzige Punkt auf unserer Liste, der gleichzeitig erhalten bleibt und nicht von Beobachtern diskutiert wird.

Sie müssen sich nur daran erinnern, dass die Masse des Objektsystems nicht die Summe der Massen der Objekte ist, aus denen das System besteht, sondern was durch Gleichung Nr. 1 'gegeben ist.

Dann versuchen Sie es zu erklären, sehen Sie einfach, wie es funktioniert. Ein anschauliches Beispiel sagt mehr als tausend Worte. Nehmen wir als Beispiel für ein System das Modischste, nämlich das Higgs-Teilchen (mit einer Masse von 126 GeV / s ²⁾ ) und sehen, wie die verschiedenen oben gemachten Aussagen funktionieren, wenn sie in zwei Photonen zerfallen.

Ein Higgs-Teilchen, zwei Photonen und drei Beobachter

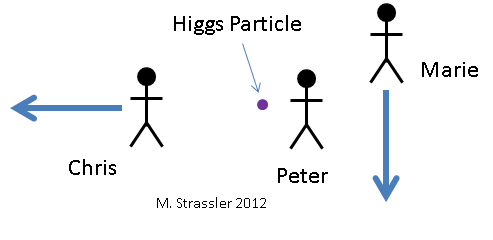Abb. 6. Drei Beobachter betrachten das Higgs-Teilchen. In Bezug auf sie bewegt sich Petja (Peter) nicht, Mascha (Marie) bewegt sich nach unten und Kostya (Chris) bewegt sich nach links.

Schauen wir uns an, wie das Higgs-Teilchen aus der Sicht von drei verschiedenen Beobachtern in zwei Photonen zerfällt. Sie sind in Abb. 1 dargestellt. 6 zusammen mit dem Higgs-Teilchen, das sie betrachten. Natürlich können sie sie nicht durch die Augen sehen, denn sie existiert zu wenig Zeit und sie ist zu klein. Sie müssen eine Art wissenschaftliche Ausrüstung verwenden. Für Petit bewegt sich das Higgs-Teilchen nicht. Mascha bewegt sich relativ zu Petit nach unten. Kostya bewegt sich relativ zu Petit nach links. Für Mascha bewegt sich das Higgs-Teilchen nach oben und für Knochen nach rechts. Drei Beobachter sehen, wie ein Teilchen gemäß Abb. 7. Petja sieht, dass Higgs in zwei Photonen derselben Energie zerfällt, von denen sich eines nach oben und das andere nach unten bewegt. Mascha sieht, dass Higgs in zwei Photonen unterschiedlicher Energie zerfällt und dass eine sich nach oben bewegende Energie mehr Energie hat als eine sich nach unten bewegende.Kostya sieht, wie Higgs in zwei Photonen zerfällt, die nach oben und unten gehen. Berechnen wir, welche Energien und Impulse von Beobachtern den Higgs und zwei Photonen zugewiesen werden und wie jeder von ihnen zu dem Schluss kommt, dass Energie und Impuls während des Zerfalls erhalten bleiben.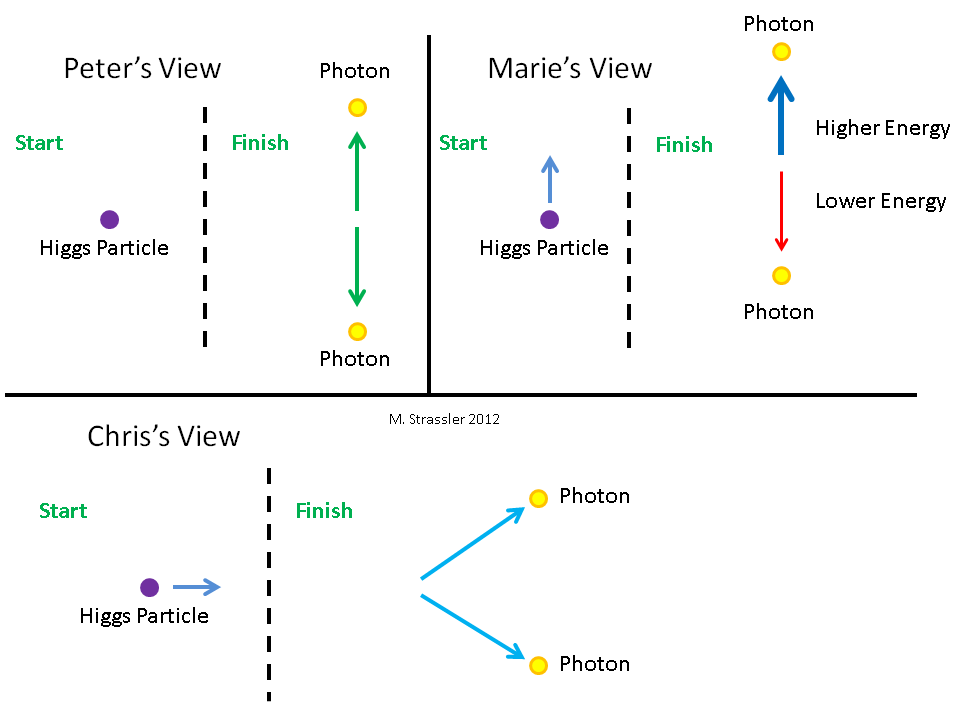

Higgs-Teilchenzerfall

Zunächst analysieren wir das Higgs-Teilchen aus der Sicht von Petit. Petja schaut (mit Messinstrumenten) auf das Higgs-Teilchen und was sieht er? (Ich werde einen Strich über alles machen, was Petja sieht, und dann vergleichen wir dies mit den Beobachtungen von Mascha und Kostya). Higgs bewegt sich nicht, also sein Schwung$$$\overline{p_0}$ist gleich Null, und gemäß Gleichung Nr. 1 he mit seiner Masse m = 126 GeV / c ^{2 wird die} Energie sein$$$\overline{E_0} = m c^2 = 126$

Entsprechend der Erhaltung von Energie und Impuls wird ein System, das aus einem Higgs-Teilchen besteht, nach dem Zerfall die gesamte Energie und den Impuls erhalten. Und das wird so sein, bis keine äußere Kraft mehr auf Higgs einwirkt. Sie können sich fragen, ob wir uns um die Schwerkraft sorgen müssen, da die Schwerkraft ein äußerer Einfluss ist, der den Impuls verändern kann. Meine Antwort ist, dass in der kurzen Zeit, in der Higgs zerfällt, die Wirkung der Schwerkraft so gering sein wird, dass Sie kichern würden, wenn ich Ihnen sagen würde, wie klein sie wirklich ist. Vergiss es.

Wenn Higgs zerfällt, sollten die Energien der Teilchen, aus denen seine Rückstände bestehen, 126 GeV betragen, und der Impuls der Teilchen (vorausgesetzt, der Impuls ist nicht nur eine Größe, sondern auch eine Richtung - ein Vektor) beträgt Null.

Die beiden masselosen Photonen, in die die Higgs zerfallen, können in jede Richtung streuen. Um das Beispiel zu vereinfachen, stellen Sie sich vor, sie streuen vertikal - eines nach oben und das andere, das von ihm abprallt, nach unten. (Wenig später werden wir diskutieren, warum sie in entgegengesetzte Richtungen fliegen sollten).

Welchen Impuls haben Photonen? Das ist einfach. Erstens muss der Gesamtimpuls des Systems - die Summe der Impulse zweier Photonen - Null sein, da Higgs vor dem Zerfall keinen Impuls hatte (aus Sicht von Petit). Jetzt hat jedes der Photonen einen Impuls einer bestimmten Größe und Richtung. Insgesamt können sie nur auf eine Weise Null geben - wenn sie gleich groß und in die entgegengesetzte Richtung sind. Wenn einer nach oben geht, sollte der andere nach unten gehen und ihre Größe sollte gleich sein.


Abb. 8: Was Petja sieht

. Zweitens ist die Gesamtenergie des Systems die Summe der Energien zweier Photonen. Dies liegt daran, dass zwischen ihnen keine Wechselwirkungsenergie besteht (mit Ausnahme einer extrem geringen Anziehungskraft, die Sie vergessen können). Da sie keine Massen haben, liegt ihre ganze Energie natürlich in der Energie der Bewegung. Zusätzlich legt Gleichung Nr. 1 für ein masseloses Teilchen nahe, dass E = pc ist, wobei p der Impuls ist. Aus diesem Grund müssen zwei Photonen mit denselben Impulsen dieselbe Energie haben. Und da sich diese beiden Energien zur Energie des Higgs-Teilchens addieren sollten, sollte die Energie jedes Photons der Hälfte der Energie des Higgs-Teilchens entsprechen.

$$ $$\overline E_1 = \overline E_2 = 1/2 (126 ) = 63$$

Und da für ein masseloses Teilchen p = E / c ist, dann

$$ $$\overline p_1 = 63 /c \uparrow \\ \overline p_2 = 63 /c \downarrow$$

Und es ist in Abb. 1 dargestellt. 8.

Energie und Impuls bleiben erhalten, Masse jedoch nicht, da Photonen keine Masse haben, Higgs jedoch. Was ist mit der Masse des Systems? Was ist die Masse eines Systems aus zwei Photonen? Nicht Null. Offensichtlich was sie ist. Ähnlich wie bei Higgs selbst (aus dem das gesamte System ursprünglich zusammengesetzt war) hat ein System aus zwei Photonen dieselbe Energie und denselben Impuls wie Higgs:

$$ $$E_{system} = \overline E_1 + \overline E_2 = 63 + 63 = 126 \\ p_{system} = \overline p_1 \uparrow + \overline p_2 \downarrow = 63 /c \uparrow + 63 /c \downarrow = 0$$

Und da für Petit $$$p_{system} = 0$ ,

$$ $$m_{system} = E_{system} / c^2 = 126 /c^2$$

Das ist die Higgs-Masse. Die Masse des Systems änderte sich während des Zerfalls erwartungsgemäß nicht.

Der Beobachter, für den Higgs aufsteigt

Mascha bewegt sich in Bezug auf Peta nach unten, also bewegen sich Petja und Higgs aus ihrer Sicht nach oben. Angenommen, Higgs bewegt sich mit einer Geschwindigkeit von v = 0,8 s, d. H. 4/5 der Lichtgeschwindigkeit relativ dazu. Im Gegensatz zu Petja hat Higgs aus Sicht von Mascha einen Impuls ungleich Null, und die Impulse der Photonen sind unterschiedlich groß, aber immer noch multidirektional - wodurch die Summe ihrer Impulse ungleich Null ist.


Abb. 9: Wie sieht Mascha den Zerfall des Higgs-Teilchens

? Wie berechnet man aus Maschas Sicht, welchen Impuls und welche Energie die Higgs und die beiden Photonen haben, in die sie zerfallen? Dazu benötigen wir einen weiteren Satz einfacher Einstein-Gleichungen. Angenommen, aus der Sicht eines bestimmten Beobachters hat das Objekt den Impuls p und die Energie E. Dann wird aus der Sicht eines anderen Beobachters, der sich mit der Geschwindigkeit v in Richtung des Objekts (oder dagegen) bewegt, der Impuls und die Energie des Objekts wie folgt ausgedrückt:

$$ $$p = γ (\overline p+ v \overline E/c^2) \qquad ( №3) \\ E = γ (\overline E + v \overline p) \qquad ( №4)$$

Wobei γ eine andere pythagoreische Gleichung erfüllt:

$$ $$1 = v^2/c^2 + 1/γ^2 \qquad ( №5)$$

nach Einstein. Dies ermöglicht es uns, Transformationen zwischen dem, was Petja sieht, und dem, was Mascha sieht (oder jedem anderen Beobachter, der sich mit Geschwindigkeit v bewegt) durchzuführen. Was wir finden, ist in Abb. 9.

Um Maschas Beobachtungen mit denen von Petya zu vergleichen, benötigen wir v und γ. Ich behaupte, wenn v = 4/5 c, dann ist γ = 5/3.

Überprüfen Sie mit Gleichung Nr. 5: 1 = (4/5) 2 + (3/5) 2 = 16/25 + 9/25 = 25/25

Petja sagt das bei Higgs$$$p_0=0, E_0=126$ .Was ist mit Mascha? Sie sagt das:

$$ $$p_0 = γ v \overline E_0 = (5/3) (4/5) \overline E_0 = 168 /c \uparrow \\ E_0 = γ \overline E_0 = (5/3) \overline E_0 = 210$$

Petja behauptet, dass zwei Photonen $$$\overline E_1 = \overline E_2 = 63$und für jeden von ihnen E = p c. Jetzt können wir anhand der Gleichungen Nr. 4 und Nr. 4 berechnen, was Mascha sieht.

$$ $$E_1= γ (1+v) \overline E_1 = 189 , p_1 = E_1/c \uparrow$$

$$ $$E_2= γ (1-v) \overline E_2= 21 , p_2 =E_2/c \downarrow$$

Es funktioniert! Energie wird auch aus Marys Sicht gespart, z

$$ $$E_0 = 210 \\ E_1 + E_2 = (189 + 21) = 210$$

Impuls wird auch gespeichert:

$$ $$p_0 = 168 /c \uparrow \\ p_1 + p_2 = 189 /c \uparrow + 21 /c \downarrow = (189 – 21) /c \uparrow = 168 /c \uparrow$$

Die Masse des Systems stimmt mit der Higgs-Masse vor und nach dem Zerfall überein, da vor und nach dem Zerfall

$$ $$E_system = 210 \\ p_system = 168 /c \uparrow$$

Was nach Gleichung Nr. 1 'die Masse des Systems zurückbringt $$$126 /c^2$ wie bei Petit, weil

$$ $$210^2 = 168^2 + 126^2$$

Der Beobachter, aus dessen Sicht sich Higgs nach rechts bewegt

Was haben wir mit Bones? Kostya bewegt sich beispielsweise relativ zu Petja mit einer Geschwindigkeit von v = 4/5 s nach links, so dass sich Higgs (und Petja) in Bezug auf Kostya mit einer Geschwindigkeit von v = 4/5 s nach rechts bewegen. Die gleichen Berechnungen, die wir für Mascha durchgeführt haben, zeigen, dass die Higgs-Energie $$$E_0 = 210 GeV und p_0 = 168 GeV$ aber im Gegensatz zu Mascha, für die sich Higgs nach oben bewegt, ist für Kostya der Higgs-Impuls nach rechts gerichtet. Dies ist in Abb. 2 dargestellt. 10.


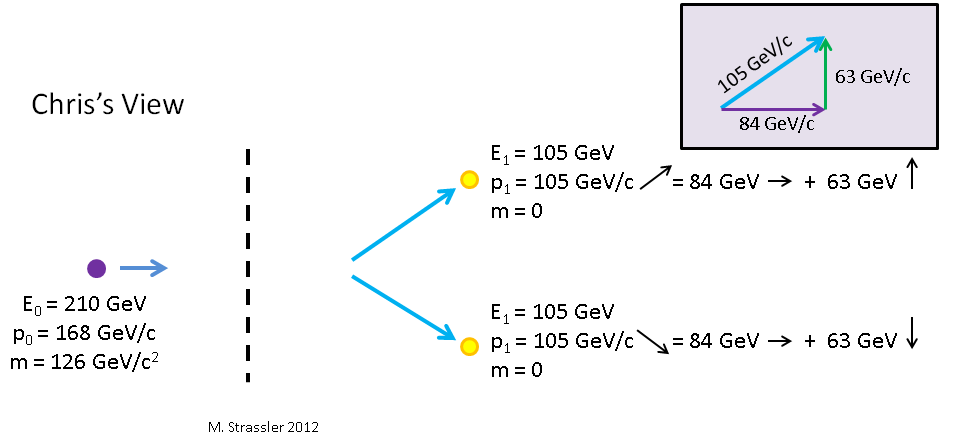
Abb. 10

Higgs zerfällt in zwei Photonen. Wenn sich aus Sicht von Petya die Photonen auf und ab bewegen, dann bewegt sich für Kostya, der beobachtet, wie sich Higgs und Petya nach rechts bewegen, eines der Photonen nach rechts und das andere nach rechts. Welchen Impuls und welche Energie werden sie dann haben?

Durch die Gleichungen Nr. 4 und Nr. 5 wissen wir dies nicht, da sie für Fälle vorgesehen sind, in denen sich das Teilchen und der Beobachter in die gleiche Richtung bewegen. Für unseren Fall lauten die Gleichungen wie folgt:

$$ $$\ updownarrow p = \ updownarrow \ overline p \\ \ leftrightarrow p = γ ([\ leftrightarrow \ overline p] + v \ overline E / c ^ 2) \\ E = γ (\ overline E + v [\ leftrightarrow \ Überstrich p])$$

Diese Gleichungen werden einfacher sein, als sie scheinen, da aus Sicht von Petit p keine Komponente hat, die sich von links nach rechts bewegt, und der gesamte Puls nach oben oder unten geht. Also beobachtet Kostya die folgenden Werte für Higgs:

$$ $$\ updownarrow p_0 = \ updownarrow \ overline p_0 = 0 \\ \ leftrightarrow p_0 = γ v \ overline {E_0} / c ^ 2 = (5/3) (4/5) 126 GeV / c = 168 GeV / c \ rechter Pfeil \\ E = γ \ overline {E_0} = (5/3) 126 GeV = 210 GeV$$

Und das Photon steigt

$$ $$\ updownarrow p_0 = \ updownarrow \ overline p_1 = 63 GeV / c \ uparrow \\ \ leftrightarrow p_0 = γ v \ overline {E_1} = (5/3) (4/5) 63 GeV / c = 84 GeV / c \ rightarrow \\ E = γ \ overline {E_0} = (5/3) 63 GeV = 105 GeV$$

Für das zweite Photon sind die Formeln gleich, nur seine vertikale Komponente ist nach unten gerichtet. Es ist zu beachten, dass für beide Photonen E = pc gemäß dem Satz von Pythagoras für die Größe p für jeden der Impulse gemäß dem Einschub in Fig. 1 gilt. 10

$$ $$p_1 ^ 2 = (\ uparrow p_1) ^ 2 + (\ rightarrow p_1) ^ 2 \\ oder \\ (105 GeV / c) ^ 2 = (63 GeV / c) ^ 2 + (84 GeV / c) ^ 2$$

Und wieder beobachtet Kostya andere Werte von Energie und Impuls im Vergleich zu Petja und Mascha. Aber für Kostya bleiben Energie und Dynamik erhalten. Kostya beobachtet auch, dass die Masse eines Systems mit zwei Photonen mit der Higgs-Masse übereinstimmt. Warum? Der gesamte vertikale Teil des Impulses des Systems ist Null, er wird gegenseitig zerstört. Der horizontale Teil des Systemimpulses beträgt 168 GeV / s. Die Gesamtenergie des Systems beträgt 210 GeV. Dies ist das gleiche, was Mascha beobachtet hat, außer dass ihr Schwung des Systems gestiegen ist und nicht nach rechts. Die Richtung des Impulses beeinflusst jedoch nicht die Gleichung Nr. 1 '. Nur seine Größe spielt dort eine Rolle. So sieht Kostya wie Mascha, dass die Masse des Systems zweier Protonen ist $$$126 GeV / c ^ 2$ gleich der Masse des primären Higgs-Teilchens.

Zusammenfassung

Wir sehen also, was drei verschiedene Beobachter beobachten. Ihre Beobachtungen:

• variieren, was Higgs Energie und Impuls sind,
• variieren in Bezug auf Energie und Impuls beider Photonen,
• sich auf die Erhaltung von Energie und Impuls während des Zerfalls einigen,
• Sie sind sich daher einig, dass die Masse des Systems erhalten bleibt.
• stimmen zu, dass die Masse des Systems 126 GeV / c ² beträgt,
• und außerdem, dass die Summe der Massen der Objekte des Systems nicht erhalten bleibt, sondern von 126 GeV / c ² auf Null abnimmt.

Und das ist kein Zufall. Einstein aus früheren Experimenten wusste, dass Energie und Impuls erhalten bleiben, und suchte und fand Gleichungen, die dieses Merkmal der Welt bewahren. Dabei stellte er auch fest, dass die Masse des Systems die Gleichung Nr. 1 'erfüllen muss.

Bonus: wie es bei der Suche nach einem Higgs-Partikel verwendet wird

Wissenschaftler:

• Protonenkollisionen beobachten, bei denen zwei Photonen geboren werden;
• Berechnen Sie die Masse eines Systems aus zwei Photonen (im Fachjargon wird dies als invariante Masse eines Photonenpaars bezeichnet).

Wenn ein Higgs-Teilchen als Ergebnis eines Experiments in zwei Photonen zerfällt, hat das System aus zwei Photonen, in das es zerfällt, unabhängig von der Richtung und Geschwindigkeit, in der sich das Teilchen in Bezug auf das Labor bewegt, immer eine Masse, die der Masse entspricht Higgs-Teilchen, die sie produziert haben! Im Gegensatz zu zufälligen Prozessen, die zu einem System aus zwei Photonen zufälliger Masse führen, erzeugen Higgs-Teilchen daher immer ein System aus zwei Photonen gleicher Masse. Wenn daher Higgs-Teilchen in den Ergebnissen eines Experiments auftreten und manchmal in zwei Photonen zerfallen, sehen wir einen Peak von Higgs-Zerfällen, der durch andere zufällige Prozesse über einen glatten Hintergrund steigt. Und so geschah es im Experiment auf dem LHC!