Die Herausforderung für Fünfjährige, die "viral" geworden ist

Die ganze Wahrheit über das neueste Virus-Puzzle aus Singapur und ein weiteres historisches Rätsel mit Zahlen



Zu Ehren des Jubiläums dieser Kolumne hat mir das Internet freundlicherweise ein singapurisches mathematisches Problem zur Verfügung gestellt, das viral geworden ist . Mitte Mai war das Internet begeistert von der Aufgabe, die Erstklässler in Singapur angeblich lösen, nämlich Kinder im Alter von 5 bis 7 Jahren, und die sich als so schwierig herausstellte, dass niemand sie lösen kann.


Studieren Sie die Zahlenfolge sorgfältig und füllen Sie die Lücken aus

In unserer Geschichte geht es jedoch tatsächlich darum, wie Ausdrücke wie „ein mathematisches Problem, das das Internet aufgewühlt hat“ zu langweiligen und vorhersehbaren Versuchen wurden, Besucher auf die Seite zu locken. Da selbst ein kurzer Blick auf diese Ausgabe, die erstmals im technischen Forum von Singapur erschien, uns sagen lässt, dass dieses Foto eine offensichtliche Fälschung ist. Das Foto sieht bearbeitet aus, aber es gibt keine Erklärung für die Aufgabe.

Anscheinend wurde das Rätsel von einer Website übernommen (und geändert), die sich mathematischen Rätseln widmet und von Gordon Burgin, einem amerikanischen pensionierten Lehrer, geleitet wird. Und in der Version von der Site im unteren linken Viertel ist die Nummer 20. Auf dem Foto in Singapur ist 0 verschmiert. Kein Wunder, dass es keine offensichtliche Lösung gibt!

"Ich bin erstaunt über diese Fälschung und weiß nicht, was sie erreichen wollten", sagt Burgin. "Wenn ihr Ziel eine hitzige Diskussion und anschließende Verzweiflung war, dann haben sie ihr Ziel erreicht!"

Als nächstes kommt das richtige Puzzle.

1. In jedem der vier Sektoren des äußeren Kreises gibt es eine zweistellige Zahl, die der Summe der drei Zahlen in den Ecken dieses Sektors entspricht. Die Zahlen in einzelnen Kreisen können von 1 bis 9 variieren, und jede der Zahlen kann nur einmal verwendet werden. Eine der Nummern wird Ihnen gegeben, um zu beginnen. Finde die restlichen vier.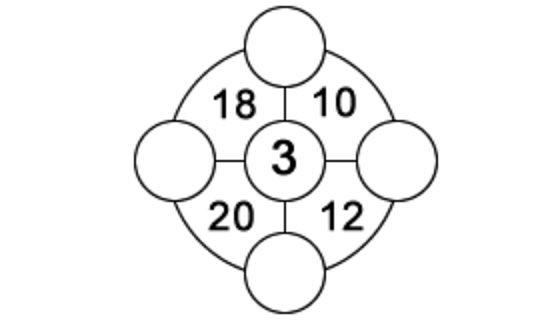



2. Da das Singapur-Rätsel falsch war, versuchen Sie, eine Variante des Problems vorzuschlagen, die für das obige Bild geeignet wäre (mit einem Nullpunkt).

Dieses Rätsel erinnerte mich an ein Rätsel aus einem der interessantesten Bücher zur Geschichte der Rätsel: " Wakoku chiekurabe ", das älteste japanische Rätselbuch , das 1727 veröffentlicht wurde. Das ist ein wunderbares Rätsel - und zumindest wurde sie gerade im Osten geboren!

3. Notieren Sie die Zahlen von 1 bis 9 in schwarzen Kreisen, sodass die Summe der Zahlen auf jedem der beiden blauen Kreise (einschließlich des Mittelkreises) sowie entlang der horizontalen und vertikalen Linien gleich ist.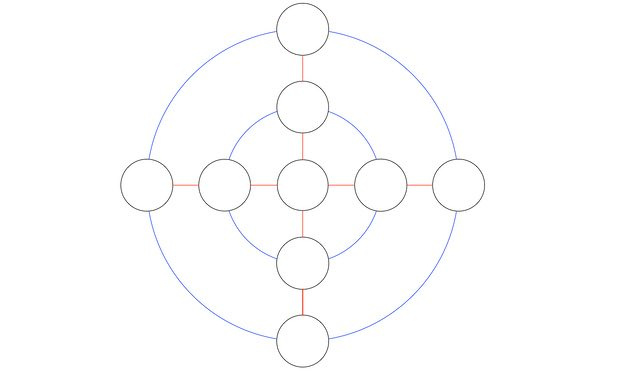



Dies sind vier Beträge, von denen jeder aus fünf Begriffen besteht, und alle Beträge sind gleich. Hier ist ein Bild aus dem Buch selbst, das eine ähnliche Aufgabe darstellt.

Lösungen

1. Im Uhrzeigersinn von oben beginnend: 6, 1, 8, 9

Wenn wir die Positionen für die Zahlen Nord, Ost, West und Süd benennen, sind die Kandidaten für West und Süd 8 und 9, da S + 3 + 3 = 20 oder S + 3 = 17. Aber wir wissen, dass S + B. + 3 = 12 oder 10 + B = 9. Aber 10 kann nicht 9 sein, denn dann ist B = 0, und dies ist verboten. Daher ist = = 8, 3 = 9, C = 6 und B = 1.

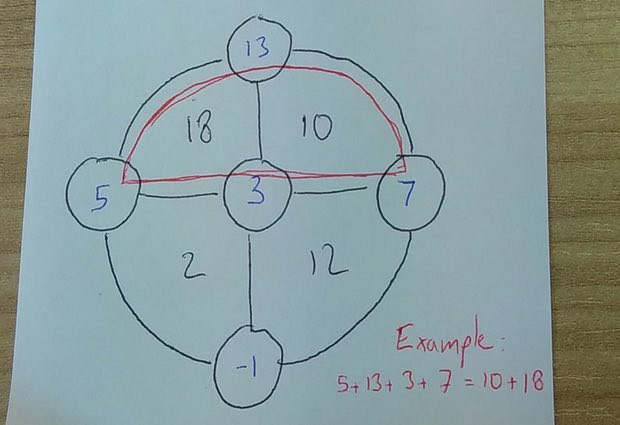
2. Was mir am besten gefallen hat, war die Aufgabe eines Lesers namens Tom Flannery, die sich als sehr einfach herausstellte.

Füllen Sie die Kreise mit ganzen Zahlen, sodass die Summe der Sektoren in jedem der Halbkreise der Summe der Zahlen in den Kreisen entspricht.

3. Und die letzte Aufgabe aus der japanischen Rätselsammlung von 1727.

Es kann viele Lösungen geben. Hier ist meine Lösung:



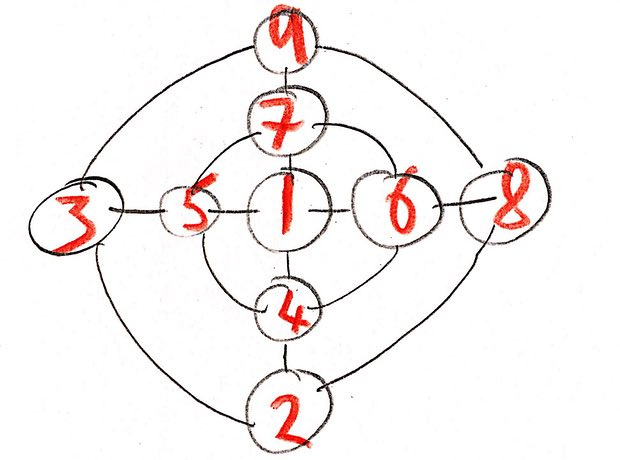
Der Weg zur Lösung hilft uns zu erraten - in der Mitte kann es nur eine ungerade Zahl geben. Nachdem Sie eine solche Zahl ausgewählt haben, müssen Sie die verbleibenden Ziffern in Paare teilen, die sich zu derselben Zahl addieren, und sie in entgegengesetzten Kreisen anordnen. Ich habe 1 für das Zentrum gewählt, es gibt Paare 2 und 9, 3 und 8, 4 und 7, 5 und 6 - alle ergeben insgesamt 11.