Wie man ein unmögliches Polyeder macht: unwirkliche reale Mathematik

Die Mathematik gibt uns ein genaues Bild von fast genauen Antworten.

Mit dickem Papier und transparentem Klebeband sammelt Craig Kaplan ein wunderschönes, abgerundetes Objekt, das der Kreation von Buckminster Fuller oder einer trendigen neuen Art von Fußball ähnelt. Es besteht aus vier regulären Dodecagons (12 Gons mit den gleichen Winkeln und Seiten) und 12 Decagons (10-seitige Polyeder) mit 28 kleinen Öffnungen in Form von gleichseitigen Dreiecken. Es gibt nur ein Problem - diese Zahl kann nicht existieren. Ein solcher Satz von Polygonen fällt nicht mit den Eckpunkten zusammen, und die Figur schließt nicht.

Das Kaplan-Modell funktioniert nur, weil Sie beim Zusammenbau aus Papier wenig Handlungsspielraum haben. Die Seiten können sich fast unmerklich verbiegen. „Die Fehlerquote, die sich aus der Arbeit in der realen Welt mit Papier ergibt, bedeutet, dass Dinge, die nicht möglich sein sollten, tatsächlich erhalten werden“, sagt Kaplan, IT-Spezialist an der University of Waterloo in Kanada.



Dies ist ein neues Beispiel aus einer Klasse unerwarteter mathematischer Objekte, auf die der amerikanische Mathematiker Norman Johnson in den 1960er Jahren gestoßen ist. Johnson arbeitete an der Fertigstellung eines Projekts, das Plato vor mehr als 2000 Jahren begonnen hatte - er erstellte einen Katalog idealer geometrischer Formen. Aus der unendlichen Vielfalt dreidimensionaler Figuren können nur fünf aus denselben regulären Polygonen erzeugt werden: Tetraeder, Oktaeder, Hexaeder, Ikosaeder, Dodekaeder. Wenn Sie verschiedene reguläre Polygone mischen, können Sie 13 weitere Figuren zusammenstellen, in denen alle Polygone auf Eckpunkte treffen - archimedische Körper - sowie Prismen (zwei identische Polygone, die durch Quadrate verbunden sind) und „Antiprismen“ (zwei identische Polygone, die durch gleichseitige Dreiecke verbunden sind).

Im Jahr 1966 entdeckte Johnson während seiner Arbeit an der Universität von Michigan 92 weitere Körper, die nur aus regulären Polygonen bestehen, die heute [in den USA] als Johnson-Körper bezeichnet werden . Und dies erschöpfte alle Möglichkeiten, die der russische Mathematiker Viktor Abramovich Zalgaller , der damals an der Leningrader Staatsuniversität arbeitete, einige Jahre später bewies. Es ist unmöglich, aus regulären Polygonen eine andere geschlossene Form herzustellen.

Aber während einer Bestandsaufnahme der Polyeder bemerkte Johnson etwas Seltsames. Er fand seine Formen und komponierte ihre Modelle aus Pappe und Gummibändern. Da es nur wenige mögliche Polyeder gibt, erwartete er, dass neue Formen ziemlich schnell erscheinen würden. Wenn Sie anfangen, Gesichter zusammen zu machen, muss die Figur unbedingt übereinstimmen. Dies ist jedoch nicht geschehen. „Beim Zusammenbau eines Stapels von Polygonen war nicht immer klar, ob ich eine gültige Form zusammengesetzt hatte“, erinnert sich Johnson.

Es mag den Anschein haben, als hätte sich das Modell zusammengesetzt, aber „wenn Sie die Berechnungen durchführen, stellt sich heraus, dass dies nicht ganz stimmt“, sagt er. Bei sorgfältiger Prüfung stellte sich heraus, dass das, was als Quadrat erschien, nicht ganz quadratisch war oder die Seiten nicht ganz flach waren. Es wäre möglich, die Gesichter leicht zu kürzen, und sie würden perfekt passen, aber dann wären sie keine regulären Polygone mehr.

In der Absicht, alle idealen Zahlen zu berechnen, legte Johnson keinen Wert auf solche "engen Treffer". "Ich legte sie beiseite und konzentrierte mich auf das Akzeptable", sagt er. Aber diese fast idealen Figuren erregten nicht nur die Aufmerksamkeit von Kaplan und anderen Mathematikliebhabern, sie wurden auch Teil eines größeren Teils der fast idealen Mathematik.

Es gibt keine genaue Definition eines „fast genauen“ Treffers. Strenge Regeln funktionieren in einer toleranten Welt nicht. Jetzt orientiert sich Kaplan bei der Suche nach nahezu korrekten Zahlen an einer ungefähren Methode: "Ein realer mathematischer Fehler, der einer Figur innewohnt, ist vergleichbar mit einem praktischen Fehler, der sich aus der Arbeit mit realen Materialien und unvollkommenen Händen ergibt." Mit anderen Worten, wenn Sie es geschafft haben, ein unmögliches Polyeder zusammenzusetzen - wenn es so nahe ist, dass Sie es als echtes ausgeben können - dann ist dies eine fast exakte Zahl. In anderen Bereichen der Mathematik sind fast genaue Ergebnisse so real, dass sie Sie täuschen oder überraschen können - eine Art mathematischer Witz.

Einige dieser mathematischen Kuriositäten können nicht mehr als einfacher Spaß genannt werden, während andere tiefe Bedeutungen in Mathematik und Physik haben können.

Die alten Probleme, einen Kreis zu quadrieren und einen Würfel zu verdoppeln, fallen in die Kategorie der fast richtigen Lösungen. Sie scheinen verlockend offen dafür zu sein, die richtige Lösung zu finden, aber am Ende erweisen sie sich als unmöglich - wie eine geometrische Figur, die geschlossen aussieht, es aber nicht ist. Einige Entwürfe von Leonardo da Vinci und Albrecht Dürer bogen leicht um die Ecken und gaben fast normale Pentagone als echte aus.



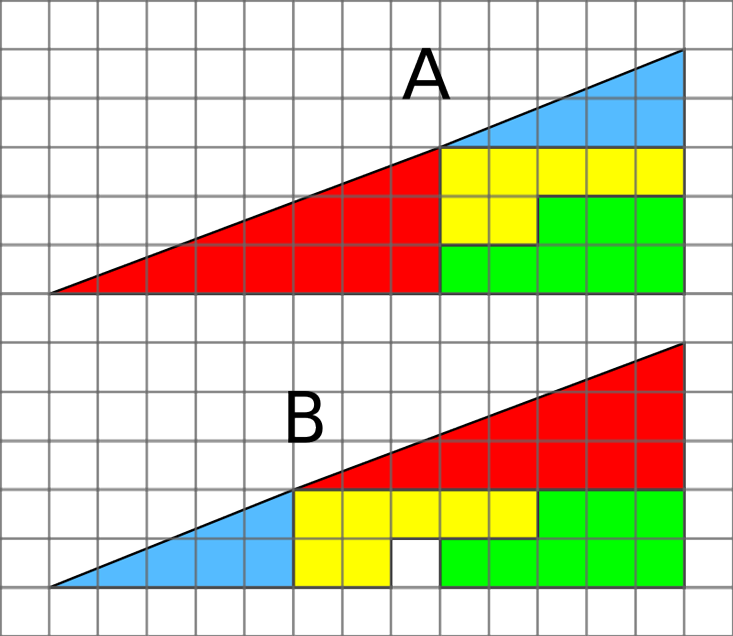
Und es gibt ein Rätsel mit einem fehlenden Quadrat. In der Figur ist ein rechtwinkliges Dreieck in vier Teile geschnitten. Wenn Sie sie neu anordnen, wird eine Lücke darin angezeigt. Woher kam er? Dies ist auch fast die richtige Entscheidung. Keines der Dreiecke ist tatsächlich ein Dreieck. Ihre Hypotenusen sind verdreht, und es ist fast unmöglich zu bemerken, weshalb die Illusion so überzeugend ist.

Digital Matching ist eine der nützlichsten Entscheidungen im Alltag. 2 ^{7/12 ist} fast gleich 3/2. Aus einem ähnlichen Grund hat das Klavier 12 Tasten in einer Oktave und ist das Herzstück des gleichmäßig temperierten Systems westlicher Musik. Dies ist ein Kompromiss zwischen den beiden wichtigsten Musikintervallen: einer Oktave (Frequenz 2: 1) und einer fünften (Frequenz 3: 2). Numerisch ist es nicht möglich, eine Oktave so zu teilen, dass alle Quinten perfekt sind. Sie können dem jedoch nahe genug kommen, indem Sie die Oktave in 12 Halbtöne unterteilen, von denen sieben eine Frequenz von 1,498 ergeben. Für die meisten Menschen ist das genug.

Manchmal treten in der Mathematik fast exakte Treffer auf, als würde sie sich selbst täuschen. In der Simpsons-Episode "Treehouse of Horror VI" bemerkten mathematisch interessierte Zuschauer etwas Ungewöhnliches: Gleichung 1782 ¹² + 1841 ¹² = 1922 ¹² . Auf den ersten Blick scheint es, als hätten die Autoren den Großen Satz von Fermat widerlegt und postuliert, dass die Gleichung x ⁿ + y ⁿ = z ⁿ keine ganzzahligen Lösungen für n> 2 enthält. Wenn Sie diese Zahlen in einen Taschenrechner eingeben, erscheint das Ergebnis korrekt. Wenn Sie jedoch Berechnungen mit einer Genauigkeit durchführen, die für die meisten Taschenrechner nicht verfügbar ist, stellt sich heraus, dass die Wurzel des 12. Grades von der linken Seite der Gleichung 1921,999999955867 und nicht 1922 ist und Fermat ruhig sein kann. Überraschend kleiner Schlupf - weniger als 10 Millionen Teile.

Aber solche fast genauen Treffer sind nicht nur Witze. "Diejenigen, die mich mehr faszinieren als andere, sind Fälle, die auf das Vorhandensein von etwas Wichtigerem hinweisen", sagt John Baez, Mathematiker an der University of California in Riverside. Dies ist der Fall bei einer Größe, die manchmal als Konstante von Ramanujan bezeichnet wird . Diese e ^{π √163-Zahl} , die ungefähr 262 537 412 640 768 743.9999999999999925 entspricht, ist überraschend nah am Ganzen. Wir können nicht erwarten, dass diese drei irrationalen Zahlen - e, π und √163 - sich irgendwie verbinden und uns eine rationale Zahl geben, ganz zu schweigen vom Ganzen. Aber es gibt einen Grund, warum sie so gut zusammenpassen. "Es ist nicht nur ein Zufall, von dem wir keine Ahnung haben", sagt Baez. "Dies ist der Schlüssel zu den Tiefen der Mathematik." Die genaue Erklärung ist ziemlich kompliziert, basiert jedoch auf der Tatsache, dass 163 die größte der Hegner-Zahlen ist . Die mit diesen Zahlen verbundenen Aussteller sind sehr nahe an ganzen Zahlen.

Oder nehmen Sie eine mathematische Verbindung, die als „monströse Mondscheinhypothese“ (monströser Mondschein) bekannt ist. Die Geschichte ist folgende: 1978 machte der Mathematiker John Mackay die triviale, ebenso interessante Beobachtung: 196 884 = 196 883 + 1. Die erste Zahl war ein Koeffizient eines wichtigen Polynoms, j-invariant , und die zweite entstand im Zusammenhang mit einem riesigen mathematischen Objekt aus der Gruppentheorie genannt " Monster ". Viele Menschen zuckten mit den Schultern und gingen weiter, aber diese Beobachtung interessierte viele Mathematiker, die beschlossen, sie näher zu untersuchen. Sie fanden eine Verbindung zwischen zwei scheinbar nicht miteinander verbundenen Themen: der Zahlentheorie und der Symmetrie von Monstergruppen. Diese Verbindung kann noch umfassendere, noch nicht offene Konsequenzen für andere Themen haben. Der Physiker Edward Whitten glaubt, dass die Monstergruppe mit der Quantengravitation und der Raum-Zeit-Struktur in Verbindung gebracht werden kann.

Mathematisch fast korrekte Treffer zeigen sowohl Verspieltheit als auch die Kraft der menschlichen Herangehensweise an die Mathematik. Johnson, Kaplan und andere machten durch Versuch und Irrtum Entdeckungen - sie studierten das Feld als Biologe, der auf der Suche nach neuen Arten durch den Dschungel watete. In der Mathematik ist es jedoch einfacher, eine systematische Suche durchzuführen. Zum Beispiel haben Jim McNeill, der sich für Mathematik als Hobby interessiert und auf seiner Website eine Sammlung fast korrekter Treffer sammelt, und Robert Webb, ein Programmierer, Software zum Erstellen und Studieren von Polyedern erstellt.

Fast genaue Treffer leben auf der unscharfen Grenze zwischen idealistischer, harter Mathematik und unseren herablassenden und praktischen Gefühlen. Sie drehen die Logik der Approximation um. Normalerweise wird die reale Welt als unvollkommener Schatten der Welt von Platon betrachtet. Die Perfektion der zugrunde liegenden Mathematik geht bei ihrer Implementierung verloren. Bei fast genauen Treffern ist die reale Welt der perfekte Schatten der unvollkommenen Welt. Annäherung ist "die falsche Annäherung an die richtige Antwort", sagt Kaplan, und "ein fast genauer Treffer ist eine genaue Darstellung einer fast genauen Antwort."

Auf diese Weise verändern fast genaue Antworten die Verbindung zwischen Mathematikern und mathematischen Physikern mit der Natur. "Ich bin dankbar für die Unvollkommenheiten der realen Welt, weil sie es mir ermöglichen, ein Quasi-Ideal zu erreichen, indem ich mit Objekten arbeite, die im Wesentlichen unvollkommen sind", sagt Kaplan. "Sie ermöglichen es mir, die Grenzen der Mathematik dank der Schönheit einer gebrochenen Realität zu überwinden."