Wir verstehen die Teilchenphysik: 1) eine Kugel auf einer Feder, die Newtonsche Version

1. Ball auf einer Feder, Newtonsche Version
2. Eine Quantenkugel auf einer Feder
3. Wellen, klassischer Look
4. Wellen, die klassische Bewegungsgleichung
5. Quantenwellen
6. Felder
7. Teilchen sind Quanten
8. Wie Partikel mit Feldern interagieren

Es ist nicht so schwierig, die Grundlagen der Teilchenphysik allgemein zu verstehen - und dies ist unser derzeitiges Verständnis der meisten elementaren Phänomene des Universums. Es wird für Sie einfacher sein, wenn Sie eine Physik- und Mathematikschule besucht oder das erste Studienjahr abgeschlossen haben. Wenn Sie sich jedoch mit Algebra, Trigonometrie und (möglicherweise, aber nicht unbedingt) den Grundlagen der Differenzierung und Integration befassen, können Sie verstehen, wie Felder funktionieren und wie Partikel erscheinen. Sie müssen mein Wort nur einmal nehmen, wenn es um einen Aspekt der Quantenmechanik geht. In diesem Fall werde ich keine mathematischen Formeln angeben, sondern Ihnen einfach die vorgefertigten Antworten zeigen. Aber nachdem Sie diesen Aspekt akzeptiert haben, wird alles andere klar sein.


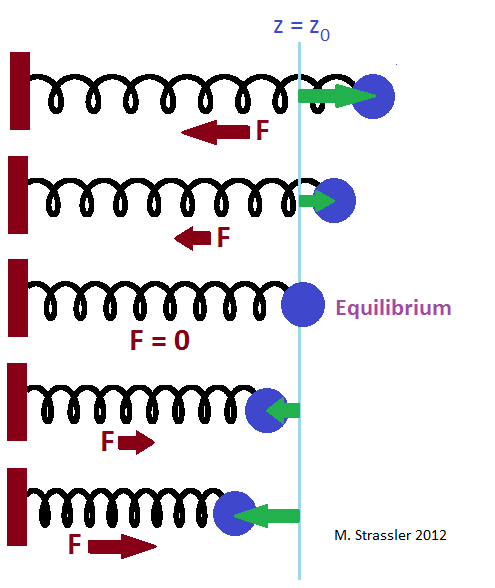Abb. 1

Um die Teilchenphysik zu verstehen, muss man sich aus der Schulphysik an eine einzige Sache erinnern - wie eine Feder funktioniert. Tatsächlich ist alles, was springt, vibriert, klingelt, klappert und hin und her schwankt, ein Beispiel für eine Feder.

Stellen Sie sich vor, wir hätten am Ende einer Feder einen Ball platziert. Die Bewegungen der Feder und die sie beschreibenden Gleichungen sind einfach. Zunächst erinnern wir uns an die Grundlagen des Federverhaltens, dann untersuchen wir das Verhalten der Kugelschwingung. Und schließlich werden wir für die neugierigsten Köpfe die Gleichungen betrachten, die zu dieser Art von Bewegung führen.

Harmonischer Oszillator (auch bekannt als Kugel auf einer Feder)

Die Kugel auf der Feder hat eine Ausgleichsposition; Wenn Sie den Ball dort hineinlegen und loslassen, drückt die Feder ihn nicht in eine Richtung und der Ball bleibt bewegungslos. Dies ist die blaue Linie in Abb. 1. Wenn Sie den Ball aus der Gleichgewichtsposition ziehen (grüne Pfeile), zieht die Feder den Ball mit Kraft F zurück (rote Pfeile). Je weiter Sie den Ball ziehen, desto stärker zieht ihn die Feder zurück (zumindest bis Sie die Feder brechen oder mit Druck brechen).

Oszillierende Bewegung (Springen)

Wir nennen die Bewegungsrichtung der Kugel "Richtung z" und definieren die z-Achse so, dass z = z ₀ der Gleichgewichtsposition der Kugel auf der Feder entspricht. Angenommen, wir ziehen den Ball aus dieser Position und halten ihn so, dass er sich nicht bewegt, in die Position z = z ₀ + A; dann geben wir es zu einem bestimmten Zeitpunkt t = 0 frei. Der Ball wird hier und da springen - siehe Abb. 2. Die Größe der Sprünge - die Amplitude der Schwingungen - ist gleich A. Sie kann beliebig groß oder klein sein; Nur Sie wählen, wie viel der Ball aus der Gleichgewichtsposition gezogen werden soll. Sie steuern jedoch nicht, wie oft Sprünge hin und her - die Frequenz der Schwingungen ν - auftreten. Es stellt sich heraus, dass es unabhängig vom Wert von A dasselbe ist. Es wird nur durch die Eigenschaften der Kugel und der Feder bestimmt und nicht durch das, was Sie tun.

Für wissenschaftliche Zwecke ist es äußerst wichtig, Beobachtungen durch eine mathematische Formel zu beschreiben. Die Position des Balls z ist eine Funktion der Zeit t, die von uns als z (t) geschrieben wird und folgende Form annimmt:

$$

$$z (t) = z_0 + A cos [2 \ pi \ nu t]$$

Wobei cos wie üblich der Cosinus ist, π die Zahl pi aus der Geometrie des Kreises ist, z ₀ die Gleichgewichtsposition der Kugel ist und A und ν (nu) die Amplitude und Frequenz der Schwingungen sind. Die Kosinusfunktion ist oszillierend, daher beschreibt diese Formel oszillatorische Bewegungen mit der Amplitude A und der Frequenz ν. Beispiele für die Schwingungsbewegung einer Kugel auf einer Feder mit unterschiedlichen Werten der Anfangsabweichung und der Gesamtamplitude A sind in Abb. 1 dargestellt. Dies zeigt auch, dass für eine gegebene Kugel auf einer Feder die Frequenz ν nicht von der Amplitude A abhängt.

Kleingedrucktes: Amplitude und Frequenz sind größer als Null. Wenn A negativ ist, ist die Amplitude –A. Tatsächlich ist die Amplitude tatsächlich | A |, dh der Größenmodul.


Abb. 2

Was ist an der Amplitude und Frequenz von Kugel und Feder (in der klassischen Vorquantenphysik) sehr wichtig zu beachten:
• Amplitude A kann beliebig gewählt werden;
• Die Frequenz ν wird durch die Kugel und die Feder bestimmt. Um eine andere Frequenz zu wählen, müssen Sie die Feder oder die Kugel ersetzen.

Die Periode jeder Schwingung (wie lange es dauert, bis der Ball genau einmal vorwärts und rückwärts geht) wird als T bezeichnet, und diese Periode ist einfach der Kehrwert der Frequenz: T = 1 / ν. Wenn der Zeitraum 5 Sekunden beträgt, beträgt die Frequenz alle fünf Sekunden oder 1/5 Sekunde (was häufig als 1/5 Hertz oder Hz bezeichnet wird).

Ein weiteres Kleingedrucktes: In jedem realen System einer Feder und eines Balls, dem Sie im Alltag begegnen, führt Reibung dazu, dass A allmählich abnimmt und schließlich Null erreicht, wenn die Bewegung stoppt. Formeln, die die Reibung während der Bewegung berücksichtigen, sind nicht viel komplizierter, aber wir werden sie nicht brauchen. Daher gehe ich immer davon aus, dass die Reibung gering ist, A sehr langsam abnimmt und wir einfach vereinfachte Formeln verwenden können, die die Reibung ignorieren. Aber es ist wichtig zu wissen: Reibung reduziert A, wirkt sich aber nicht auf ν und T aus, es sei denn, es ist extrem stark! Die Schwingungsfrequenz bleibt auch bei abnehmender Amplitude gleich. Daher ändert sich die Note, die die Gitarrensaite nach dem Ziehen erzeugt, nicht, selbst wenn der resultierende Klang allmählich verblasst.

Noch etwas: Es gibt eine schöne Formel für Energie, die in einer oszillierenden Feder gespeichert ist. Es ist proportional zum Quadrat der Amplitude und zum Quadrat der Frequenz:

$$

$$E = 2 \ pi ^ 2 \ nu ^ 2 A ^ 2 M$$

Zum Teil ist dies die Bewegungsenergie des Balls (kinetisch) und zum Teil die im Frühjahr gespeicherte Wechselwirkungsenergie (Potential). Wenn der Ball hin und her schwankt, ändern sich die Anteile dieser Energien an der Gesamtenergie ständig. Die Gesamtenergie E bleibt jedoch konstant.

Kleingedrucktes: Es gibt immer noch die Energie der Masse des Balls, Mc ² , aber wir verfolgen sie nicht, weil sie immer da ist, die Feder sich mitbewegt oder nicht.

Die gleiche Schwingungsformel gilt für fast alles, was zittert oder springt, nur wenn diese Sprünge nicht zu groß sind. Eine Kugel rollt am Boden der Schüssel entlang; ein Auto, das auf schlechte Stoßdämpfer springt; vibrierende Saite einer Geige oder Gitarre; Xylophonstange nach dem Schlagen; usw.

Die Gleichung der Schwingungsbewegung (mathematische Sprünge)

Erinnern wir uns nun an die Grundformeln, die uns erklären, warum die Kugel auf der Feder schwingt.

Wie eingangs erwähnt (Abb. 1), hat die Kugel auf der Feder eine Gleichgewichtsposition, die wir z = z ₀ nannten. Angenommen, zu einem bestimmten Zeitpunkt (entweder haben wir den Ball gezogen oder er hat gezögert) befindet er sich in einer anderen Position, z. Wenn z> z ₀ ist, dh wenn die Verschiebung von der Gleichgewichtsposition z - z ₀ größer als Null ist, erzeugt die Feder eine Kraft, die in die negative Richtung z gerichtet ist, um die Kugel zurück zum Gleichgewichtspunkt zu ziehen. Wenn umgekehrt z <z ₀ ist, dh die Verschiebung vom Gleichgewicht z - z ₀ negativ ist, erzeugt die Feder eine Kraft, die in die positive Richtung z gerichtet ist, um die Kugel wieder zum Gleichgewichtspunkt zurückzuziehen. Und je weiter der Ball von der Gleichgewichtsposition entfernt ist, desto stärker zieht die Feder. Die durch die Feder erzeugte Kraft F hängt mit der Verschiebung der Kugel aus dem Gleichgewicht durch die Gleichung zusammen

$$

$$F = - K (z - z_0)$$

Wobei K ein positiver Wert ist, der von einer bestimmten Feder abhängt und als Konstante der Feder bezeichnet wird.

Beachten Sie, warum diese Formel wahr ist:

• Befindet sich der Ball in der Gleichgewichtsposition, ist F = 0. Die Feder erzeugt keine Kraft, und wenn sich der Ball nicht in der Gleichgewichtsposition bewegt hat, bleibt er dort.
• Wenn die Abweichung größer als Null ist, ist die Kraft negativ.
• Wenn die Abweichung negativ ist, ist die Kraft positiv.
• Je größer die Abweichung ist, desto größer ist die Stärke.

Dann wenden wir uns Newtons zweitem Bewegungsgesetz zu, das besagt, dass sich unter dem Einfluss der Kraft F ein Ball der Masse M mit der Beschleunigung a bewegt, wobei F = M a. Ersetzen Sie dies in der Formel und erhalten

$$

$$M a = - K (z - z_0)$$

oder

$$

$$a = - K / M (z - z_0)$$

Dies ist für uns eine fast notwendige Gleichung, aus der wir die Schwingungsgleichung ableiten können. Wir müssen uns nur an die Beziehung zwischen a und z erinnern. Dazu ist es wichtig, die Beziehung zwischen a und Geschwindigkeit v sowie zwischen v und z in Erinnerung zu rufen. Dieses Verhältnis ist eine von zwei Änderungen im Laufe der Zeit:
• Geschwindigkeit ist eine zeitliche Änderung der Position, v = dz / dt
• Beschleunigung ist eine Änderung der Geschwindigkeit im Laufe der Zeit, a = dv / dt

Hinzufügen und erhalten

$$

$$a = d (dz / dt) / dt = d ^ 2z / dt ^ 2$$

Beschleunigung ist die zeitliche Änderung einer Positionsänderung im Laufe der Zeit.

Wir können unsere Bewegungsgleichung umschreiben

$$

$$d ^ 2z / dt ^ 2 = - K / M (z - z_0) \ quad (*)$$

Wobei z eine kurze Notation für z (t) ist. Und jetzt können wir überprüfen, ob die Schwingungsbewegung z (t) = z ₀ + A cos [2 π ν t] eine Lösung für diese Bewegungsgleichung ist. Wir müssen zuerst die Geschwindigkeit eines Teilchens als Änderung seiner Position in der Zeit berechnen:

$$

$$d / dt (z_0 + A cos [2 \ pi \ nu t]) = - (2 \ pi \ nu) A sin [2 \ pi \ nu t]$$

(dz ₀ / dt = 0, da sich die Gleichgewichtsposition z ₀ nicht mit der Zeit ändert und d / dt (cos wt) = -w sin wt); und dann berechnen wir die Beschleunigung des Teilchens als Änderung seiner Geschwindigkeit über die Zeit:

$$

$$d / dt [- (2 \ pi \ nu t)] = - (2 \ pi \ nu) ^ 2 A cos [2 \ pi \ nu t]$$

(da d / dt (sin wt) = w cos wt). Ergebend

$$

$$d ^ 2z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 A cos [2 \ pi \ nu t] = - (2 \ pi \ nu) ^ 2 (z - z_0)$$

Wo ich im letzten Schritt die Formel z (t) = z ₀ + A cos [2 π ν t] für die Schwingungsbewegung verwendet habe. Die endgültige Gleichung ist dieselbe wie unsere Bewegungsgleichung [ $$$d ^ 2z / dt ^ 2 = - K / M (z - z_0)$], vorausgesetzt, dass (2 π ν) ² = K / M ist, wenn die Schwingungsfrequenz ist

$$

$$ν = \ frac {\ sqrt {K / M}} {2 \ pi}$$

Tatsächlich haben wir festgestellt, dass unsere Bewegungsgleichung impliziert, dass die Feder mit der angegebenen Frequenz schwingt, dass diese Frequenz nicht von A abhängt - sie hängt nur von den Eigenschaften der Feder (K) und der Kugel (M) ab - und das unabhängig davon von der Größe A für die Gleichung gibt es eine Lösung. Daher können wir ein beliebiges A wählen, je nachdem, wie weit wir den Ball aus der Gleichgewichtsposition ziehen, bevor wir ihn loslassen.

Resonanz

Resonanz ist eines der wichtigsten Naturphänomene, sowohl im normalen Leben, wo sie in vielen Aspekten der Technologie und in der Musik eine Rolle spielt, als auch in den grundlegenden Prozessen der physikalischen Welt, insbesondere in der Teilchenphysik.

Denken Sie zunächst daran, wie die Schaukel funktioniert. Ein Schwung, wie ein Ball auf einer Feder oder ein Pendel, ist ein Oszillator - er schwankt mit einer bestimmten Frequenz hin und her, die nicht von der Schwungamplitude abhängt. Im Falle eines Schwungs bleibt diese Aussage wahr, bis die Amplitude sehr groß ist. Sie wissen wahrscheinlich aus Erfahrung, dass Sie, um ein Kind höher zu schwingen, den Schwung einmal pro Zyklus nach vorne schieben müssen, damit die Schwungamplitude ständig zunimmt. Wenn Sie den Schwung mehrmals pro Zyklus oder alle zweieinhalb Zyklen nach vorne schieben, erhöhen Sie manchmal die Amplitude des Schwungs und verringern ihn manchmal. Offensichtlich ist es etwas Besonderes, die Frequenz, mit der Sie den Schwung drücken, an der Eigenfrequenz des Schwungs selbst auszurichten.

Wenn das Kind selbst weiß, wie man den Schwung schwingt, weiß es, dass es seine Beine gleichzeitig mit der Eigenfrequenz des Schwungs schwingen muss, um die Schwungamplitude zu erhöhen. Schwingen Sie anders und die Amplitude wächst nicht.



Sie können verfolgen, wie dies mit dem Ball auf der Feder geschieht. Schau dir das Bild an. Auf der linken Seite schwingt eine Kugel um eine Gleichgewichtsposition hin und her. Er zögert ohne äußere Erschütterungen. Sie schwingt mit der Eigenfrequenz der Feder ν. Die Frequenz ist √ K / M, wobei K die Federkraft ist, M die Masse der Kugel ist.

Rechts in Abb. Sie können sehen, was mit einer anderen schwarzen Kugel passiert, deren Masse der ersten entspricht, auf derselben Feder, die mit der Kraft F gedrückt wird (ihre Größe und Richtung werden durch den roten Pfeil angezeigt), die mit einer von ν verschiedenen Frequenz ν _F schwingt. Ein schwarzer Ball verhält sich wie eine Schaukel, die zu selten drückt. Sie bewegen sich in einem komplexen Muster und klettern nicht hoch. In Abb. Es ist zu sehen, dass der Ball nicht sehr gleichmäßig schwingt und die Amplitude der Schwingungen gering ist. Sie können sehen, wie er versucht, mit einer Eigenfrequenz zu schwingen, obwohl seine allgemeine Bewegung mit einer Frequenz ν _F wiederholt wird.

Dann zeigt die Figur den Fall, in dem die Kraft mit einer Frequenz ν _F schwingt, die viel höher als die Frequenz ν ist. Wieder können Sie sehen, wie er "versucht", mit einer Eigenfrequenz zu schwingen, aber es gelingt ihm nicht, dies mit einer großen Amplitude zu tun, da eine schnell oszillierende Kraft sie entweder in oder gegen eine Bewegung drücken und die Amplitude erhöhen oder verringern kann .

Und am Ende wird der Fall gezeigt, wenn die Kraft mit der Eigenfrequenz der Feder schwingt, ν _F = ν. Der Ball reagiert sehr unterschiedlich: Die Amplitude der Schwingungen wächst ständig, und der schwarze Ball schwingt genauso leicht und gleichmäßig wie der weiße Ball links, jedoch mit zunehmender Amplitude. Dies ist eine Resonanz.

Infolgedessen: Wenn sich ν _F von ν unterscheidet - wenn die Kraft nicht zulässt, dass der Ball in die Resonanz eintritt -, bewegt er sich widerstrebend und seine Bewegung unterscheidet sich stark von der natürlichen, von einer einfachen Schwingung mit der Frequenz ν. Im Gegenteil, wenn die Frequenz der Kraft der natürlichen entspricht - wenn die Kraft den Ball in Resonanz bringt - dann drückt die Kraft den Ball viel effizienter und die resultierende Bewegung ist beeindruckender. Wir wissen das intuitiv; Wenn das Kind (oder die Eltern) den Schwung mit einer Eigenfrequenz drückt, schwingt es den Schwung immer höher.

Zu den wichtigen Aspekten der Resonanz in der Teilchenphysik gehört die Tatsache, dass Teilchen unter bestimmten Umständen aufgrund eines sehr ähnlichen Mechanismus erzeugt werden können: Nach einer Kollision zweier Teilchen wird eine Kraft mit genau der Frequenz erhalten, die zur Erzeugung eines dritten Teilchens erforderlich ist.

Nächstes Mal: ​​Quantenball auf einer Feder

Dies ist das Verhalten eines Balls auf einer Feder in der klassischen Vorquantenphysik. Die Quantenmechanik verändert viele Konzepte , aber das Wichtigste ist: Wir können immer noch A wählen, aber A kann keine Größe haben. Es können nur bestimmte Werte angenommen werden, die proportional zur Quadratwurzel von ganzen Zahlen sind.