Wir verstehen Teilchenphysik: 3) Wellen, klassische Form

1. Ball auf einer Feder, Newtonsche Version
2. Eine Quantenkugel auf einer Feder
3. Wellen, klassischer Look
4. Wellen, die klassische Bewegungsgleichung
5. Quantenwellen
6. Felder
7. Teilchen sind Quanten
8. Wie Partikel mit Feldern interagieren

Nachdem wir uns mit den Gleichungen für Schwingungen befasst haben - die fast alles beschreiben, was springt, vibriert, hin und her rollt, wie eine Kugel auf einer Feder -, können wir uns dem ebenso verbreiteten Naturphänomen Wellen zuwenden. Wellen sind überall: Schall und Licht, Erdbeben, Wellen auf der Oberfläche des Teiches usw.


Abb. 1

Aber vorher warne ich Sie, dass der Begriff „Welle“ irreführend sein kann, da er in der Physik nicht dasselbe bedeutet wie in Englisch. In der Physik bedeutet dies nicht, was wir normalerweise eine Welle am Rande des Ozeans nennen würden - einen Kamm und eine Mulde. In der Physik sind Wellen eine Folge von Wellen, mehrere Grate und Täler, die sich zusammen in die gleiche Richtung bewegen. In einer Welle der einfachsten Form haben alle Grate die gleiche Höhe und sind um einen Abstand voneinander beabstandet. Wir werden einen solchen Fall betrachten.

Wellen sind ein herausragendes Phänomen, wenn Sie darüber nachdenken. Stellen Sie sich vor, Sie und Ihr Freund hätten ein langes Seil genommen und es im Raum festgezogen (Abb. 2). Stellen Sie sich dann vor, Ihr Freund plauderte mehrmals mit einem Ende des Seils (grün) auf und ab. Am Ende des Seils erscheint eine Welle, die durch den Raum bis zum Ende des Seils geht (rot).


Abb. 2

Das ist erstaunlich. Ich meine - es ist wirklich erstaunlich, stark und kritisch für alles in unserem Universum, auch für Sie persönlich. Schau was passiert ist. Keines der physischen Objekte bewegte sich von links nach rechts - bevor Ihr Freund begann, das Ende des Seils zu bewegen, wurde es über den Raum gespannt, und am Ende, nachdem Ihr Ende des Seils aufgehört hat zu vibrieren und die Welle verschwindet, bleibt das Seil durch das Ganze gespannt Zimmer, wie es war. Und doch! Energie und Informationen bewegten sich im Raum. Die Welle auf dem Weg trägt die Energie, die Ihr Freund für die Vibrationen des Seils verbraucht - und in ihrer Form Informationen darüber, wie oft und wie schnell er daran gezogen hat - zu Ihnen, wo Ihre Hand zittert. Und in diesem Fall wird sie Ihnen genauso oft und in dieser Reihenfolge die Hand schütteln. Wow! Kein einziges physisches Objekt bewegte sich durch den Raum, und Energie und Informationen bewegten sich.

Oder warten. Aber sollten wir die Welle nicht als physisches Objekt betrachten? So physisch wie das Seil selbst?

Wenn wir uns an diese tiefste Frage erinnern, wenden wir uns einer kleinen Anzahl mathematischer Formeln zu, die zur Beschreibung des Erscheinungsbilds und des Verhaltens der Welle erforderlich sind, und verwenden dann etwas mehr Mathematik, um die Gleichungen aufzuschreiben, deren Lösungen die Wellen sind. Dies ähnelt dem, was wir für einen klassischen Frühlingsball gemacht haben.

Formel für eine unendliche Welle zu einem bestimmten Zeitpunkt

Diese Artikelserie unmittelbar nach dem Ball auf der Feder geht zu den Wellen, weil die Welle eine Art Doppeloszillator ist. Es schwankt sowohl zeitlich als auch räumlich. Wir werden die Zeit mit dem Buchstaben "t" und den Raum mit "x" bezeichnen.

Achten Sie auf Abb. 3. Es zeigt eine Welle, die sich über eine große Entfernung in beide Richtungen erstreckt und auf die viele Grate und Vertiefungen passen. Dies unterscheidet sich von der Welle in Abb. 2, die nur wenige Grate und Vertiefungen hat. Dieser Unterschied ist jedoch irrelevant - in Abb. 2 Ich musste veranschaulichen, wofür die genaue Wellenform keine Rolle spielte. Jetzt konzentrieren wir uns auf die mathematische Formel für die Wellen, und es ist viel einfacher, wenn die Welle eine große Anzahl von Graten und Vertiefungen derselben Größe aufweist. Dieser Fall wird sich auch als sehr nützlich erweisen, um zu verstehen, wie die Quantenmechanik das Verhalten von Wellen beeinflusst.



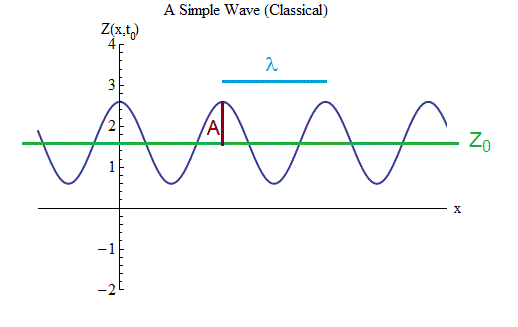
Abb. 3

Zuerst müssen wir die Notation bestimmen und eine Formel aufschreiben, die die Bewegung und Wellenform in Abb. 1 beschreibt. 3, wie wir es für den Ball im Frühjahr getan haben.

Die Grafik zeigt die Größe der Welle Z als Funktion des Raums in einem bestimmten Zeitraum t = t ₀ - wir zeichnen dies als Z (x, t ₀ ) auf. Wenn wir die Welle im Raum verfolgen, sehen wir, dass sie vorwärts und rückwärts schwingt und Z periodisch zunimmt und abnimmt. Zu jedem Zeitpunkt schwingt die Welle im Raum.

Beachten Sie, dass Z nicht mit der physischen Entfernung in Beziehung stehen muss. Es kann die Höhe des Seils sein, wie in Abb. 2, oder es kann etwas völlig anderes sein, zum Beispiel die Temperatur der Luft an einem bestimmten Punkt in Raum und Zeit oder die Ausrichtung eines magnetischen Atoms an einem bestimmten Ort eines Magneten. Aber x repräsentiert immer noch die physikalische Entfernung und t ist die Zeit.

Der Schuss dieser Welle, Z (x, t ₀ ), hat drei interessante Eigenschaften, von denen zwei auch für eine Kugel auf einer Feder gelten.

1. In der Mitte liegt ein Gleichgewichtswert Z ₀ zwischen dem größten Z-Wert auf dem Grat und dem kleinsten Z-Wert in der Vertiefung. Meistens untersuchen wir Wellen, für die Z ₀ = 0 ist, da der Wert Z ₀ oft keine Rolle spielt - aber nicht immer.
2. Die Welle hat eine Amplitude A, einen Wert, um den sich Z vom Gleichgewichtswert zur Oberseite jedes Kamms oder um denselben Wert zur Unterseite jeder Vertiefung ändert.
3. Die Welle hat eine Länge - den Abstand λ zwischen benachbarten Graten oder, was gleich ist, zwischen benachbarten Mulden oder, was gleich ist, den doppelten Abstand zwischen dem benachbarten Grat und dem Trog. Es beschreibt Schwingungen im Raum auf die gleiche Weise, wie eine Periode (gleich 1 / Frequenz) die zeitliche Schwingung einer Kugel auf einer Feder beschreibt.


Abb. 4

Was uns an die Form in Abb. 3? Es sieht aus wie ein Diagramm der Sinus- oder Cosinusfunktion - siehe Abb. 4, wobei cos (w) auf w aufgetragen ist. Cos (w) ist eine oszillierende Funktion, die eine offensichtliche Gleichgewichtsposition bei Null aufweist, deren Amplitude 1 ist und deren Wellenlänge 2π beträgt. Wie geht man von Abb. 4 zur Formel für die Welle in Abb. 3? Zuerst multiplizieren wir cos (w) mit A, so dass die Amplitude gleich A ist. Dann addieren wir Z ₀ zur gesamten Formel, um sie auf den gewünschten Gleichgewichtswert zu verschieben (wenn A = 0 ist, gibt es keine Schwingung und alles ruht am Punkt Z = Z. ₀ ). Und schließlich ersetzen Sie w durch 2πx / λ, da cos (w) Grate bei w = 0 und w = 2 π hat, daher haben Grate bei cos (2πx / λ) bei x = 0 und x = λ. Alles in allem gibt es uns

$$

$$Z (x, t_0) = Z_0 + A cos (2 \ pi x / \ lambda)$$

Dies ist fast dieselbe Formel, die die Bewegung einer Kugel auf einer Feder in der Zeit beschreibt:

$$

$$z (t) = z_0 + A cos (2 \ pi \ nu t) = z_0 + A cos (2 \ pi t / T)$$

Wobei ν die Schwingungsfrequenz ist und T = 1 / ν die Schwingungsperiode ist. Siehe die Analogie: Eine Periode bezieht sich auf die Zeit, während sich eine Wellenlänge auf den Raum bezieht.

Noch eine Anmerkung, bevor wir fortfahren. Ich könnte auch schreiben:

$$

$$Z (x, t_0) = Z_0 + A cos (- 2 \ pi x / \ lambda)$$

Da cos [w] = cos [-w]. Die Tatsache, dass wir das Minus in der Wellenformformel leicht ersetzen können, wird später wichtig sein.

Formel für eine endlose Welle an einem bestimmten Ort

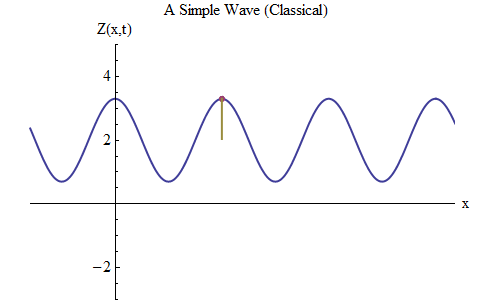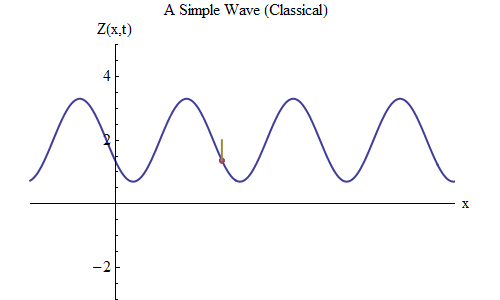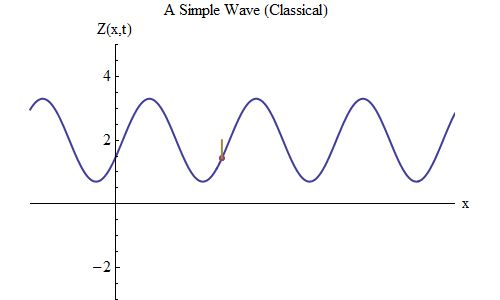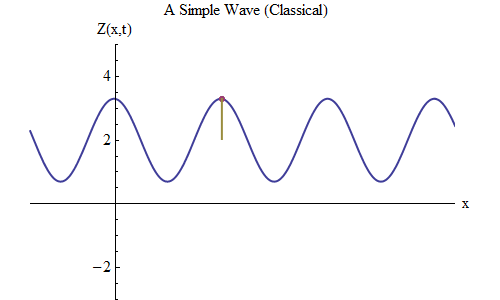Abb. 5

Stellen wir nun eine andere Frage: Lassen Sie uns sehen, wie sich die Welle mit der Zeit ändert, einen bestimmten Punkt auf dem Seil verfolgen und wie sie sich verhält und bewegt. Dies ist in Abb. 2 dargestellt. 5: dort habe ich einen bestimmten Punkt x _{0 bezeichnet} , der sich zum Zeitpunkt t ₀ auf dem Kamm befindet. Die Welle bewegt sich nach rechts und folgt der Größe der Welle Z am Punkt x ₀ , wobei sich die Zeit ändert: Z (x ₀ , t). Und Sie werden sofort sehen, dass sich die Wellenhöhe an einem bestimmten Punkt genau wie eine Kugel auf einer Feder verhält! Daher hat es genau die gleiche Formel wie eine Kugel auf einer Feder, als Funktion der Frequenz ν oder der Periode T = 1 / ν, wobei T die Zeit zwischen dem Moment ist, in dem sich die Welle bei x ₀ auf dem Scheitel befindet, und dem Moment, in dem Beim nächsten Mal nähert sie sich wieder dem Wappen.

$$

$$Z (x_0, t) = Z_0 + A cos (2 \ pi \ nu t) = Z_0 + A cos (2 \ pi t / T)$$

Schließe die unendliche Wellenformel ab

Nun brauchen wir eine Formel für Z (x, t), die die in Abb. 3 und 5 (oder eine ähnliche) an den Punkten x zu jedem Zeitpunkt t. Die richtige Antwort lautet:

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi [\ nu t - x / \ lambda]) = Z_0 + A cos (2 \ pi [t / T - x / \ lambda])$$

Es enthält beide Formeln für einen festen Zeitpunkt und für einen festen Raum.

Beachten Sie das Minuszeichen vor x. Ich erwähnte, dass Sie in der Formel für Z (x, t ₀ ) nach Belieben ein Minus ersetzen können. Mit einem Minus vor x und einem Plus vor t beschreibt die Formel eine Welle, die sich wie in Animationen nach rechts bewegt. Um dies zu überprüfen, beachten Sie, dass bei t / T - x / λ = 0 die Welle ein Scheitel ist, da cos [0] = 1 ist. Wenn t = 0 ist, ist am Punkt x = 0 der Grat. Wenn wir uns jedoch ein wenig vorwärts bewegen, beispielsweise um T / 10, befindet sich der Scheitel am Punkt x = λ / 10 rechts von der Stelle, an der er sich bei t = 0 befand - daher bewegt sich der Scheitel (und die gesamte Welle) nach rechts.

Was ändert sich, wenn Sie in der Formel für Z (x, t) ein Plus anstelle eines Minus setzen? Dann befindet sich der Scheitelpunkt bei t / T + x / λ = 0, und in diesem Fall befindet sich der Scheitelpunkt bei t = T / 10 bei x = -λ / 10 links von der Stelle, an der er sich bei t = 0 befand - was bedeutet Jetzt bewegt sich die Welle nach links (Abb. 6).


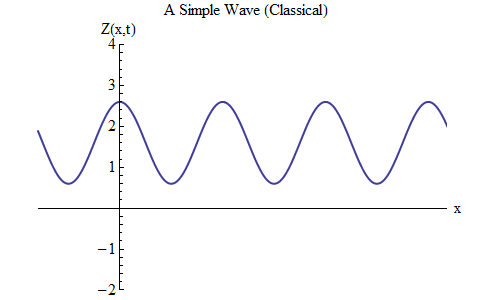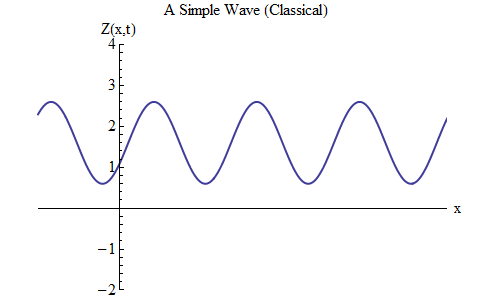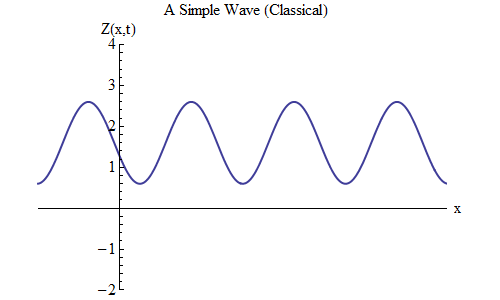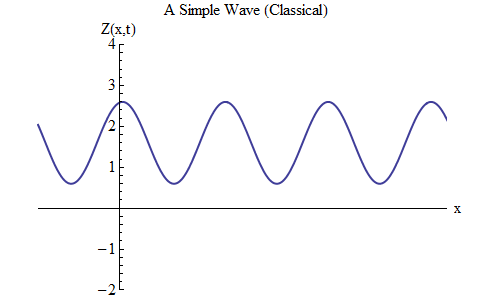Abb. 6

Die Wellen, die Funktionen von x und t sind, können sich in jede Richtung bewegen, daher müssen wir nur die richtige Formel für die gegebene Welle auswählen. Wenn wir mit Wellen arbeiten, die sich nicht nur entlang einer räumlichen Dimension x, sondern entlang aller drei Koordinaten x, y und z bewegen können, können sich diese Wellen im Allgemeinen in jede Richtung bewegen, und wir müssen die richtige Formel basierend auf der Richtung auswählen Wellenbewegung.

Kleingedrucktes: Wir können ein Minuszeichen vor t und nicht vor x setzen. Aber + t, + x ist dasselbe wie –t, -x, da dies gleichbedeutend ist mit der Multiplikation der gesamten Formel innerhalb des Kosinus mit -1 und cos [w] = cos [-w]. Daher geben + t, + x und -t, -x eine Welle, die sich nach links bewegt, und + t, -x und -t, + x geben eine Welle an, die sich nach rechts bewegt.

Wellengleichung

Nun, wie im Fall einer Kugel auf einer Feder, als wir zuerst eine Formel für die Schwingungsbewegung der Kugel fanden und dann die Bewegungsgleichung betrachteten, für die diese Formel eine Lösung war, werden wir hier dasselbe tun. Wir haben eine Formel für die Form und Bewegung der Welle gefunden. Welche Bewegungsgleichung unter den Lösungen hat eine solche Formel? Wir lernen im nächsten Artikel.