Wir verstehen die Teilchenphysik: 7) Teilchen sind Quanten

1. Ball auf einer Feder, Newtonsche Version
2. Eine Quantenkugel auf einer Feder
3. Wellen, klassischer Look
4. Wellen, die klassische Bewegungsgleichung
5. Quantenwellen
6. Felder
7. Teilchen sind Quanten
8. Wie Partikel mit Feldern interagieren

Schließlich haben wir unser Ziel erreicht: zu verstehen, was diese Dinge, die wir "Teilchen" nennen, tatsächlich Elektronen, Photonen, Quarks, Gluonen und Neutrinos sind. All dies gilt natürlich für die moderne Wissenschaft. Es sei daran erinnert, dass es in der Wissenschaft keine Garantie dafür gibt, dass das derzeitige Verständnis nicht weiter vertieft wird.

Im vorherigen Artikel wurde beschrieben, was Felder sind - Objekte, die zu jedem Zeitpunkt im Raum und zu jedem Zeitpunkt eine Bedeutung haben (Funktionen von Raum und Zeit), die Bewegungsgleichung erfüllen und physikalisch bedeutsam sind, da sie Energie von einem Ort zum anderen übertragen können und beeinflussen die physikalischen Prozesse des Universums.

Wir haben gelernt, dass die meisten uns bekannten Felder eine Eigenschaft eines Mediums beschreiben, beispielsweise die Höhe eines Seils oder den Druck in einem Gas. Wir haben aber auch gelernt, dass es in der Einstein-Relativitätstheorie eine spezielle Klasse von Feldern gibt, relativistische Felder, die kein Medium benötigen. Oder zumindest wenn sie eine Umgebung haben, ist dies sehr ungewöhnlich. Nichts in den Feldgleichungen erfordert das Vorhandensein eines Mediums und gibt nicht an, welche Eigenschaft dieses Mediums durch relativistische Felder beschrieben wird.

Daher werden wir relativistische Felder vorerst als elementare physikalische Objekte des Universums betrachten und nicht als bestimmte Eigenschaften eines unbekannten Mediums. Ob ein solcher Standpunkt von den Physikern weiter unterstützt wird, wird die Zeit zeigen.

Wir haben zwei Klassen relativistischer Felder betrachtet und werden sie nun genauer untersuchen. Sie erfüllen entweder die Bewegungsgleichung der Klasse 0, wobei c _w = c ist (wobei c die universelle Geschwindigkeitsbegrenzung ist, die oft als "Lichtgeschwindigkeit" bezeichnet wird).

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

Oder Bewegungsgleichungen der Klasse 1, wobei cw = c

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - (2 \ pi \ mu) ^ 2 (Z - Z_0)$$

Im vorherigen Artikel wurde gezeigt, dass μ die minimale Wellenfrequenz in solchen Feldern ist. In diesem Artikel werden wir es mit ν _{min bezeichnen} .

Warum wird die universelle Geschwindigkeitsbegrenzung oft als Lichtgeschwindigkeit bezeichnet? Wellen mit einer Gleichung der Klasse 0 bewegen sich mit der Geschwindigkeit c _w . Licht (ein allgemeiner Begriff, der elektromagnetische Wellen jeder Frequenz bezeichnet), die sich durch den leeren Raum bewegen, erfüllt die relativistische Gleichung der Klasse 0, daher bewegen sich die Lichtwellen (und die Wellen aller relativistischen Felder, die die relativistische Gleichung der Klasse 0 erfüllen) mit der Geschwindigkeit c.

Darüber hinaus haben wir im selben Artikel gesehen, dass, wenn ein Feld der Klasse 1 eine Welle mit der Amplitude A, der Frequenz ν, der Wellenlänge λ und dem Gleichgewichtszustand Z _{0 hat} , die Bewegungsgleichung erfordert, dass die Frequenz und die Wellenlänge mit μ = in Beziehung stehen ν _min erscheint in den Gleichungen durch die Formel

$$

$$\ nu ^ 2 = (c / \ lambda) ^ 2 + \ mu ^ 2 = (c / \ lambda) ^ 2 + \ nu_ {min} ^ 2$$

Dies ist eine pythagoreische Formel - sie kann, falls gewünscht, in Form eines Dreiecks dargestellt werden, wie in Abb. 1. Die minimale Frequenz einer Welle beträgt ν _min , und die Zuordnung ν = ν _min (und daher als λ → ∞) entspricht der Kompression des Dreiecks zu einer vertikalen Linie (Abb. 1 unten). Sie können auch eine ähnliche Beziehung der Klasse 0 erhalten, indem Sie μ = ν _min Null machen. Dann können Sie die Quadratwurzel extrahieren und erhalten

$$

$$\ nu = c / \ lambda$$

Dies ist ein Dreieck, das auf eine horizontale Linie komprimiert ist (Abb. 1, rechts). In diesem Fall ist die Mindestfrequenz Null. Das Feld kann beliebig langsam schwanken.


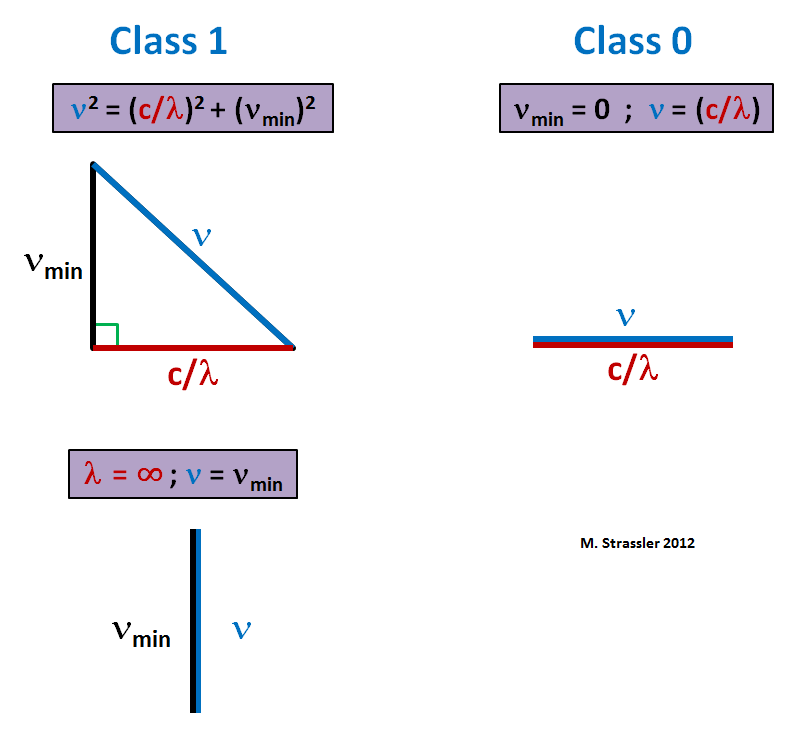Abb. 1

Es gibt keine Einschränkungen für A. Aber das liegt daran, dass wir die Quantenmechanik ignorieren. Es ist an der Zeit, relativistische Quantenfelder zu untersuchen.

Relativistische Quantenfelder

Die reale Welt ist quantenmechanisch, daher kann die Amplitude A keine sein. Es werden diskrete Werte verwendet, die proportional zur Quadratwurzel von n sind, einer nicht negativen ganzen Zahl, die die Anzahl der Schwingungsquanten in der Welle angibt. Die in der Welle gespeicherte Energie ist

$$

$$E = (n + 1/2) h \ nu$$

Wobei h die Planck-Konstante ist und notwendigerweise dort erscheint, wo die Quantenmechanik wichtig ist. Mit anderen Worten, die mit jedem Schwingungsquantum verbundene Energie hängt nur von der Frequenz der Schwingungen der Welle ab und ist gleich

$$

$$E = h \ nu$$

Dieses Verhältnis wurde erstmals 1905 von Einstein in seiner Erklärung des photoelektrischen Effekts speziell für Lichtwellen vorgeschlagen.

Aber erinnern wir uns an unser pythagoreisches Verhältnis von Frequenz und Wellenlänge. Wenn wir es mit h ² multiplizieren, erhalten wir das für ein Quantenfeld der Klasse 1

$$

$$E ^ 2 = (h \ nu) ^ 2 = (h c / \ lambda) ^ 2 + (h \ nu_ {min}) ^ 2 \ quad (*)$$

Es kommt mir bekannt vor. Wir wissen bereits, dass jedes Objekt in der Einstein-Relativitätstheorie die Gleichung erfüllen muss, die seine Energie, seinen Impuls und seine Masse beschreibt:

$$

$$E ^ 2 = (pc) ^ 2 + (mc ^ 2) ^ 2$$

Eine andere pythagoreische Beziehung. Die minimale Energie des Objekts ist mc ² , was der Aussage über die minimale Frequenz ähnelt, die eine Welle der Klasse 1, ν _min , besitzen kann. Wir könnten versucht sein, dies wahrscheinlich für ein Quantum eines relativistischen Feldes anzunehmen

$$

$$p c = h c / \ lambda \ quad (**)$$

$$

$$m c ^ 2 = h \ nu_ {min} \ quad (***)$$

Die erste Gleichung erschien erstmals 1924 in der Arbeit von Louis De Broglie - fast 20 Jahre nach Einstein. Warum hat es so lange gedauert? Ich weiß nicht.


Abb. 2

Ist das sinnvoll? Wie bereits erwähnt, umfassen relativistische Felder der Klasse 0 auch elektrische Felder, und ihre Wellen sind elektromagnetische Wellen, dh Licht. Die Version der Formel (*), die wir für Quanten der Klasse 0 erhalten, ist dieselbe wie für Felder der Klasse 1, für die μ = ν _min gleich Null ist - das heißt m = 0. Wir extrahieren die Quadratwurzel und erhalten

$$

$$E = p c$$

Oder die Einstein-Gleichung für masselose Teilchen. Und die Quanten elektromagnetischer Wellen (einschließlich aller Arten von Licht: sichtbare, ultraviolette, infrarote, Radiowellen, Gammastrahlung usw., die sich nur in der Frequenz und damit in der Energie der Quanten unterscheiden) werden wirklich masselose Teilchen sein - sobald wir die angegebenen anwenden über ein paar Gleichungen (**) und (***). Das sind Photonen.

Aus der Gleichung (***) können wir schließlich die Masse des Teilchens berechnen. Jedes Teilchen mit einer Masse ist ein Quantum eines Feldes der Klasse 1. Die minimale Frequenz solcher Wellen beträgt ν _min . Die minimale Energie eines Quantums einer solchen Welle ist gleich dem h-fachen der Frequenz. Und die Masse des Teilchens ist einfach die minimale Energie geteilt durch c ² .

$$

$$m = h \ nu_ {min} / c ^ 2$$

Wenn wir verstehen wollen, woher die Teilchenmasse kommt, müssen wir verstehen, was ν _{min bestimmt} und warum es im Allgemeinen eine Mindestfrequenz gibt. Für Teilchen wie Elektronen und Quarks ist dies völlig unklar, aber es ist bekannt, dass das Higgs-Feld dabei eine wichtige Rolle spielt.

Wir schließen daraus: Teilchen der Natur sind Quanten relativistischer Quantenfelder. Masselose Teilchen sind Quanten von Feldwellen, die eine Gleichung der Klasse 0 erfüllen. Diejenigen, die Masse besitzen, entsprechen den Feldern einer Gleichung der Klasse 1. Es gibt viele Arten von Details, aber diese Tatsache ist eine der grundlegenden Eigenschaften unserer Welt.

Verhalten sich diese Quanten wirklich wie Teilchen?

Wir stellen uns Partikel als Staubpartikel oder Sandkörner vor. In diesem Sinne sind Quanten keine Teilchen - dies sind Wellen, die für eine bestimmte Frequenz eine minimale Energie und Amplitude haben. Aber sie verhalten sich so sehr wie Partikel, dass uns vergeben werden kann, wenn wir das Wort "Partikel" in ihrer Beschreibung verwenden. Mal sehen warum.

Wenn Sie eine Welle im Wasser aufnehmen und sie durch flach unter der Oberfläche liegende Steine ​​laufen lassen, kreuzt ein Teil der Welle die Steinlinie und ein Teil wird reflektiert, wie in Abb. 3. Welcher Teil der Welle die Linie überquert, hängt von der Form der Steine, ihrer Nähe zur Oberfläche usw. ab. Die Quintessenz ist jedoch, dass ein Teil der Welle durch die Steine ​​übertragen wird und ein Teil reflektiert wird. Ein Teil der Wellenenergie geht in die gleiche Richtung, ein Teil in die entgegengesetzte Richtung.


Abb. 3

Wenn Sie jedoch ein Photon in Richtung des reflektierenden Glases senden, wird dieses Photon entweder durch dieses hindurchtreten oder reflektiert (Abb. 4). Genauer gesagt, wenn Sie das Verhalten eines Photons messen, werden Sie herausfinden, ob es reflektiert oder übertragen wird. Wenn Sie nicht messen, ist es unmöglich zu sagen, was passiert ist. Willkommen im Sumpf der Quantenmechanik. Ein Photon ist ein Quanten. Seine Energie kann nicht in den Teil unterteilt werden, der durch das Glas ging, und den Teil, der reflektiert wurde - denn dann gibt es auf jeder Seite weniger als ein Quantum, was verboten ist. (Kleingedrucktes: Glas ändert die Photonenfrequenz nicht, sodass die Energie nicht auf zwei oder mehr Quanten niedrigerer Frequenzen aufgeteilt werden kann.) Das Photon verhält sich in diesem Fall also wie ein Teilchen, obwohl es eine Welle ist. Es wird entweder vom Glas reflektiert oder nicht. Ob es reflektiert wird oder nicht, die Quantenmechanik sagt dies nicht voraus. Es gibt nur die Wahrscheinlichkeit der Reflexion. Aber sie sagt voraus, dass das Photon, egal was passiert, als Einheit wandern und seine Identität bewahren wird.


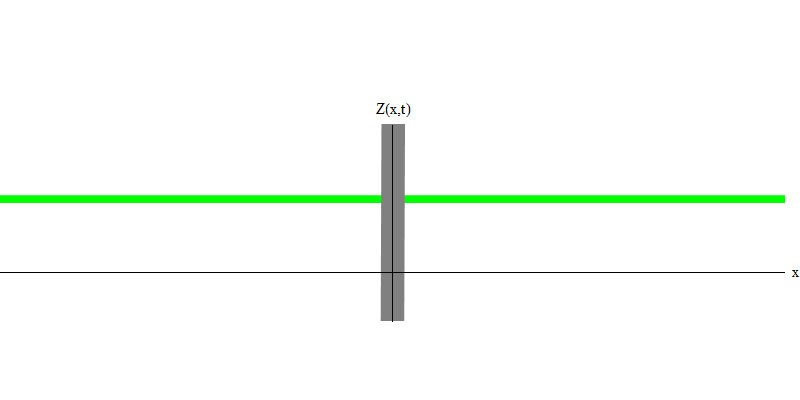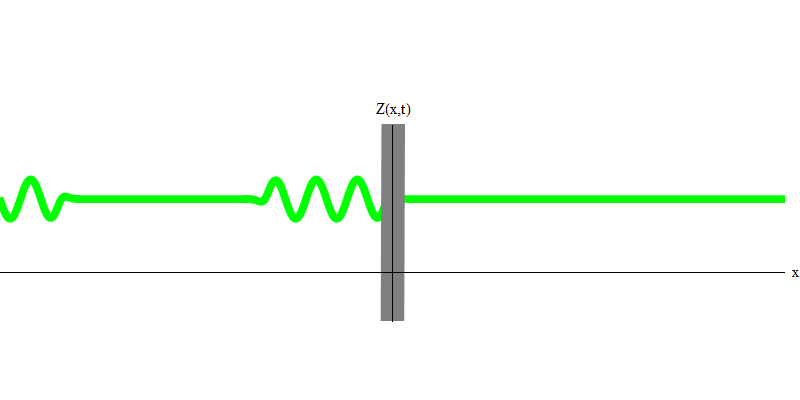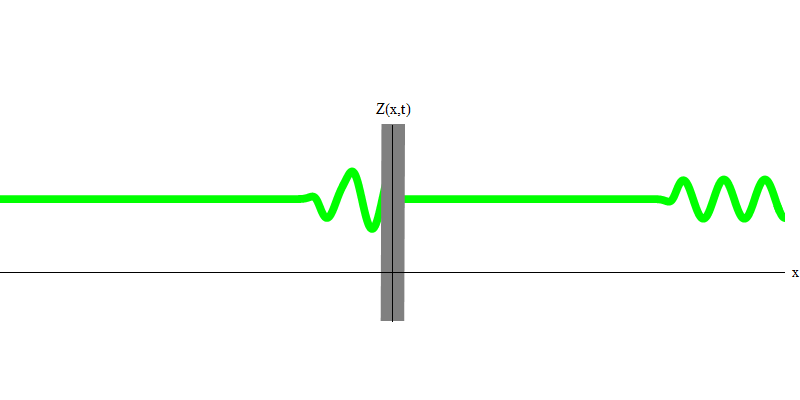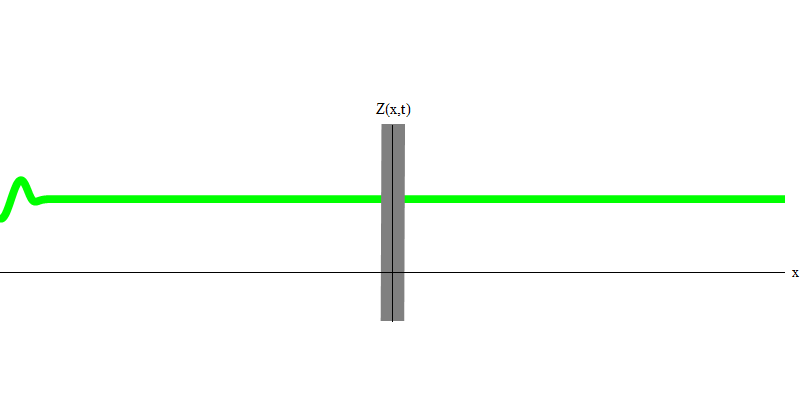Abb. 4

Und was wird mit den beiden Photonen passieren? Es kommt darauf an. Wenn beispielsweise Photonen zu unterschiedlichen Zeiten von unterschiedlichen Orten emittiert werden, sieht der Beobachter zwei im Raum getrennte Quanten, die sich wahrscheinlich in unterschiedliche Richtungen bewegen (Abb. 5). Sie können unterschiedliche Frequenzen haben.


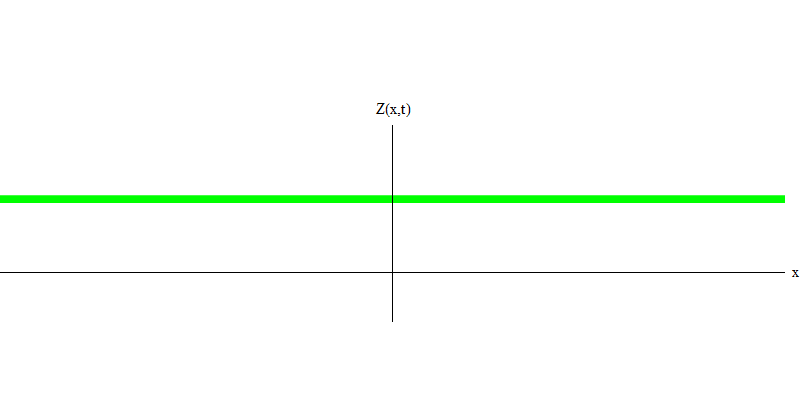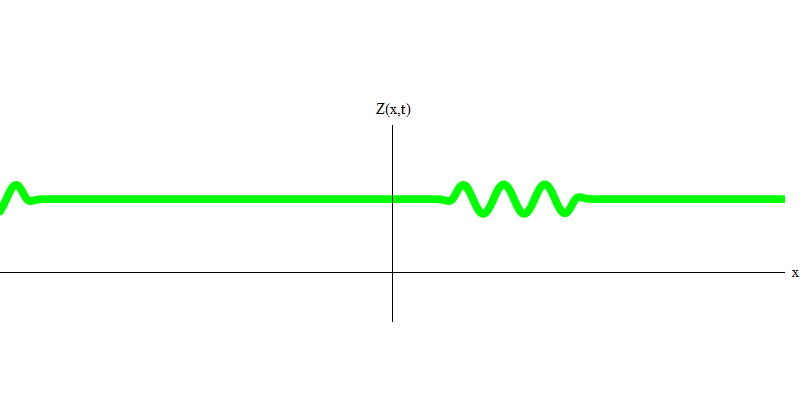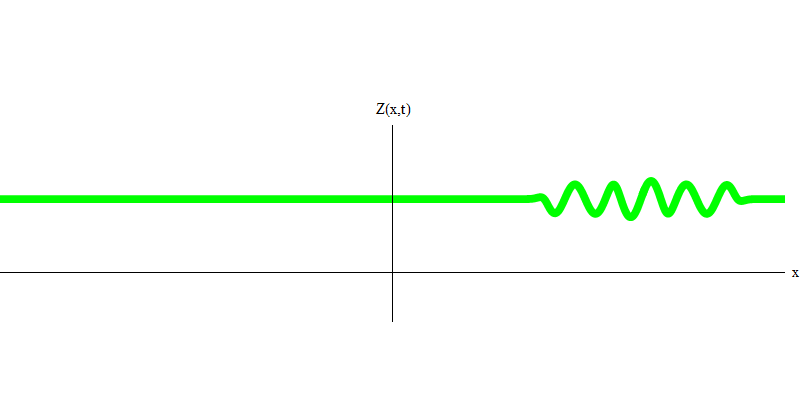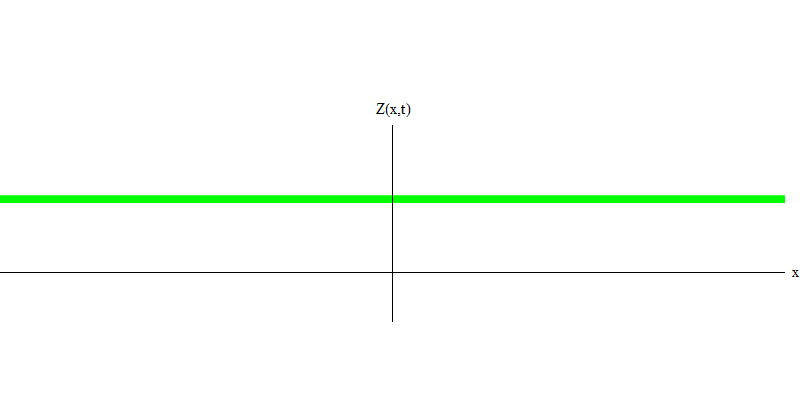Abb. 5: unabhängige Quanten

In dem speziellen Fall verhalten sich zwei Photonen, wenn sie zusammen und perfekt synchron emittiert werden (wie bei Lasern), wie in Fig. 1 gezeigt. 6. Wenn wir eine Kombination von zwei Photonen an das Glas senden, können nicht zwei, sondern drei Dinge passieren. Entweder passieren beide Photonen das Glas oder beide werden reflektiert oder eines wird passieren und das andere wird reflektiert. 0, 1 oder 2 Photonen werden vom Glas reflektiert - es gibt keine anderen Optionen. In diesem Sinne verhalten sich Lichtquanten wieder wie Teilchen, wie kleine Kugeln. Wenn Sie zwei Kugeln in ein Gitter mit Löchern werfen, werden 0, 1 oder 2 Kugeln vom Gitter reflektiert, und 0, 1 oder 2 Kugeln gehen durch die Löcher . Es gibt keine Möglichkeit, dass 1.538 Tore aus dem Netz reflektiert werden.


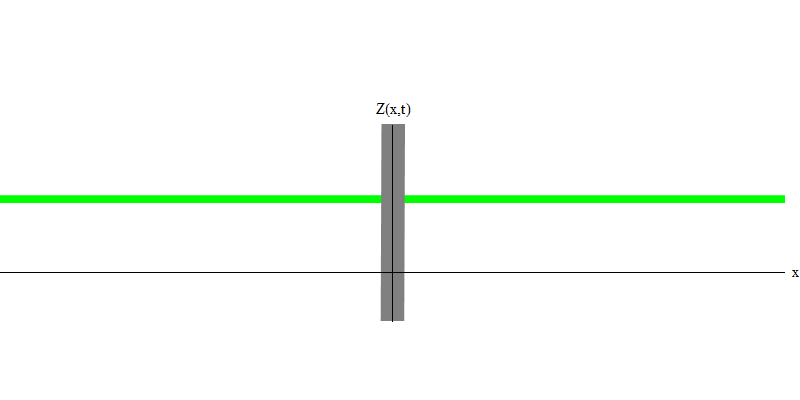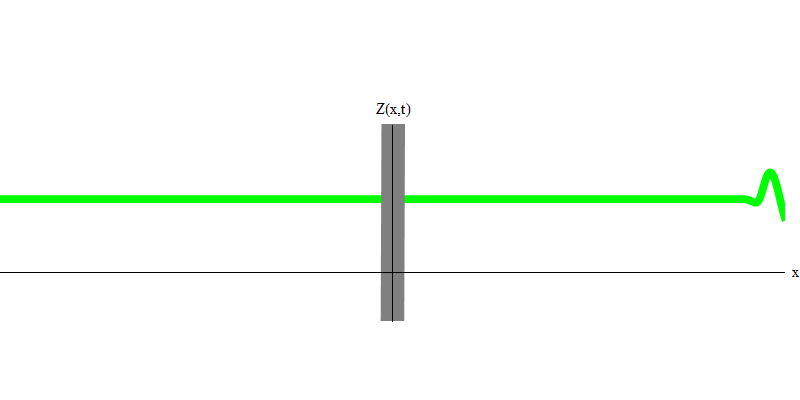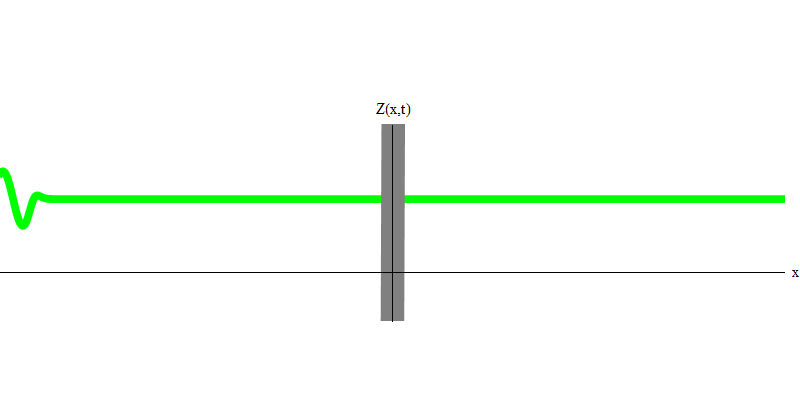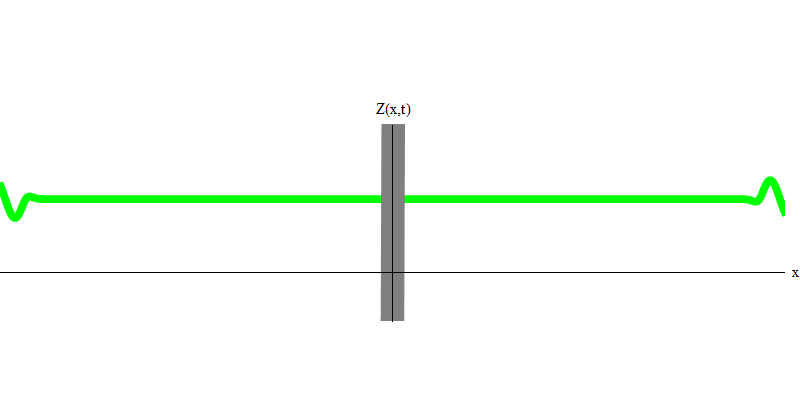Abb. 6

Dies sind jedoch Photonen, die sich ohne Masse mit Lichtgeschwindigkeit und E = p c bewegen müssen. Was ist mit Teilchen mit Masse wie Elektronen? Elektronen sind Quanten des elektrischen Feldes und können wie Photonen als Ganzes emittiert, absorbiert, reflektiert oder übertragen werden. Sie haben eine gewisse Energie und Dynamik, $$$E ^ 2 = (pc) ^ 2 + (m_e c ^ 2) ^ 2$wobei _me die Masse des Elektrons ist. Der Unterschied zwischen Elektronen und Photonen besteht darin, dass sie sich langsamer als Licht bewegen und daher ruhen können. Die Skizze eines solchen Ereignisses (in der Quantenmechanik kann aufgrund des Unsicherheitsprinzips nichts wirklich statisch sein) eines stationären Elektrons ist in Abb. 1 dargestellt. 7. Dies ist eine Welle mit minimaler Frequenz, die durch Zuweisen einer Wellenlänge mit einem sehr großen, nahezu unendlichen Wert erhalten wird. Daher ist die räumliche Wellenform in Fig. zeigt keine Windungen - es schwankt nur in der Zeit.


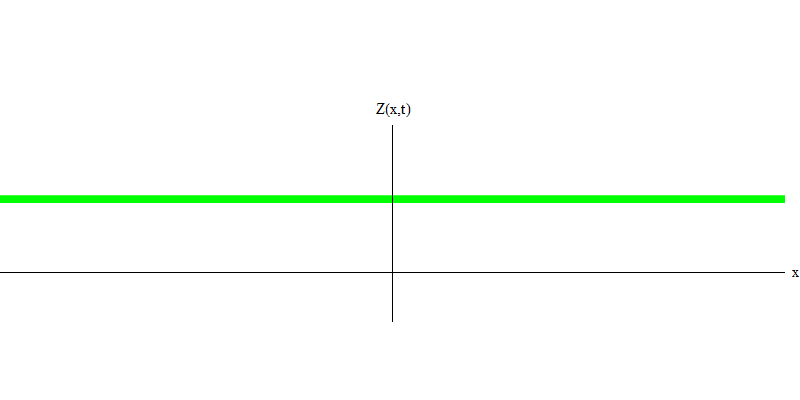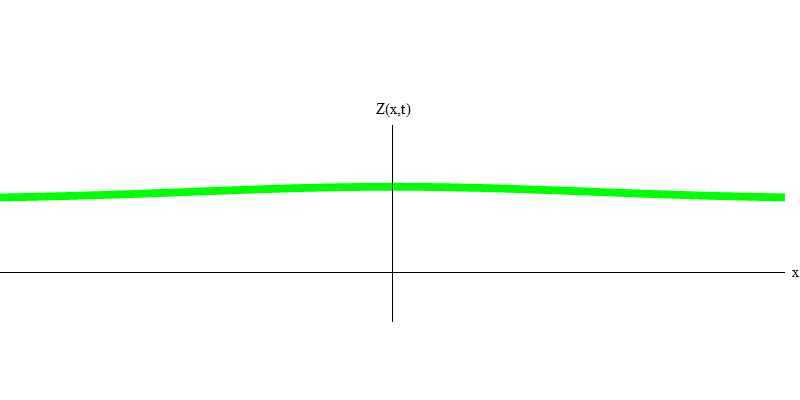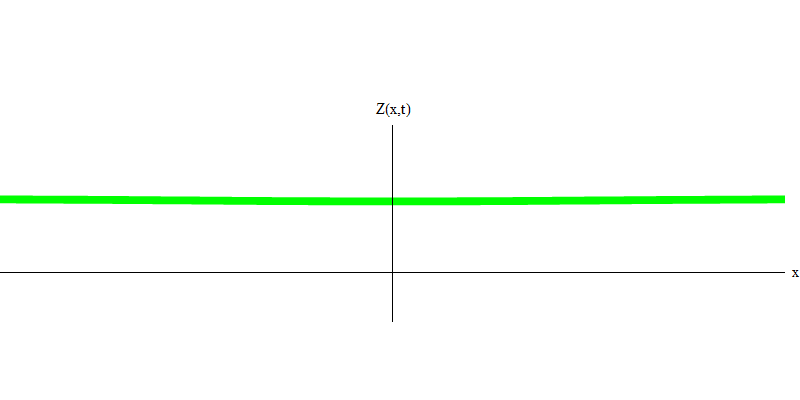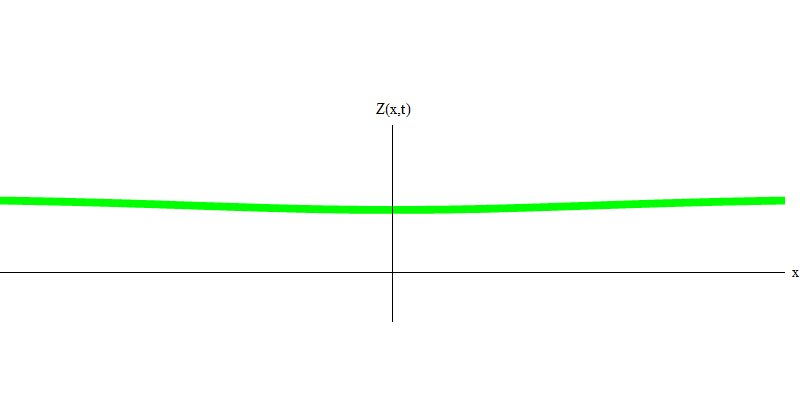Abb. 7

Ja, Quanten verhalten sich also sehr ähnlich wie Teilchen, und daher ist es keine katastrophale Täuschung, Elektronen, Quarks, Neutrinos, Photonen, Gluonen, W-Teilchen und Higgs-Teilchen als "Teilchen" zu bezeichnen. Aber das Wort "Quantum" ist dafür besser geeignet - denn das sind genau Quanten.

Wie unterscheiden sich Fermionen und Bosonen voneinander?

• Alle Elementarteilchen sind in Fermionen und Bosonen unterteilt.
• Fermionen (einschließlich Elektronen, Quarks und Neutrinos) erfüllen das Pauli-Ausschlussprinzip - zwei Fermionen desselben Typs können nicht dasselbe tun.
• Bosonen (einschließlich Photonen, W- und Z-Teilchen, Gluonen, Gravitonen und Higgs-Teilchen) sind unterschiedlich: Zwei oder mehr Bosonen desselben Typs können dasselbe tun.

Deshalb können Laser aus Photonen hergestellt werden - da sie Bosonen sind, können sie sich im selben Zustand befinden und einen starken Strahl eines Lichts erzeugen. Ein Laser kann jedoch nicht aus Elektronen bestehen, die Fermionen sind.

Wie manifestiert sich dieser Unterschied in der Sprache der Mathematik? Es stellt sich heraus, dass die Formeln, die ich mitbringe, für Bosonen geeignet sind und für Fermionen geändert werden müssen - leicht, aber mit großen Konsequenzen. Für Bosonen haben wir:

$$

$$E = (n + 1/2) h \ nu, \ quad wobei \; n = 0, 1, 2, 3, 4, ...$$

Dies bedeutet, dass die Energie jedes Quanten gleich h ν ist. Dies impliziert, dass Bosonenquanten dasselbe tun können; Wenn n größer als 1 ist, besteht die Welle im Bosonischen Feld aus mehreren Quanten, die zusammen schwingen und sich bewegen. Aber für Fermionen:

$$

$$E = (n - 1/2) h \ nu, \ quad wobei \; n = 0 \; oder \; 1$$

Die Energie eines Quanten ist immer noch gleich h ν, so dass die gesamte Diskussion der Teilchen und ihrer Energien, Impulse und Massen gültig bleibt. Die Anzahl der Quanten in einer Elektronenwelle kann jedoch nur 0 oder 1 betragen. Zehn Elektronen können im Gegensatz zu zehn Photonen nicht in einer Welle mit größerer Amplitude organisiert werden. Daher gibt es keine Fermionswellen, die aus einer großen Anzahl von Fermionen bestehen, die schwingen und sich zusammen bewegen.