Das Buch "Ein kleines Buch über Big String Theory"

Die Stringtheorie wird oft als "Theorie von allem" bezeichnet, weil sie alle grundlegenden Wechselwirkungskräfte im Universum beschreibt, einschließlich der Schwerkraft, der Quantenmechanik und der Relativitätstheorie. Dieses revolutionäre Konzept führt ein neues Verständnis von Raum und Zeit ein und versucht, den Zusammenhang zwischen Phänomenen wie Schwarzen Löchern und Quark-Gluon-Plasma, zusätzlichen Dimensionen und Quantenfluktuationen zu erklären.

Trotz der Komplexität dieses Themas bietet Stephen Gabser, Professor an der Princeton University, eine umfassende, erschwingliche und unterhaltsame Einführung in diesen heute am meisten diskutierten Bereich der Physik. Mit einem Minimum an Mathematik erklärt der Autor anhand interessanter Analogien die Essenz von Supersymmetrie, Dualität und Krümmung der Raum-Zeit, so dass es jedem Leser mit einem Vorrat an Kenntnissen der High School klar wird.

Obwohl die Bestimmungen der Stringtheorie nicht endgültig bewiesen wurden, erlauben uns diese Geheimnisse, die uns bereits offenbart wurden, die harmonische Harmonie des Universums zu bewundern und die praktische Anwendung zukünftiger Entdeckungen in der Hochenergiephysik zu diskutieren.

Schwerkraft versus Quantenmechanik

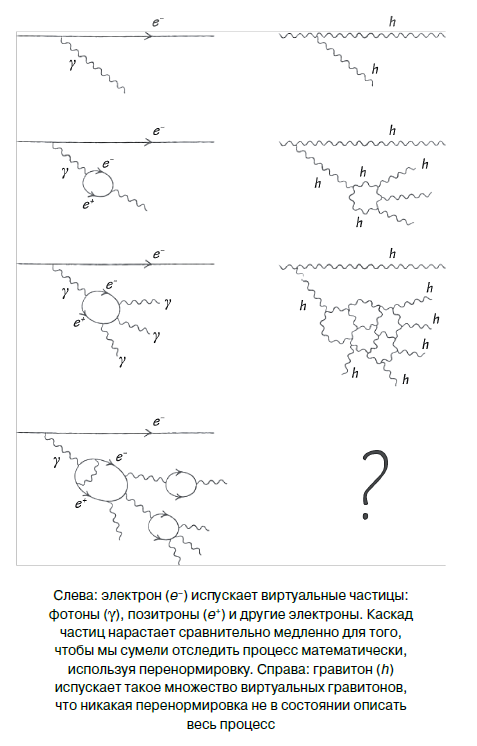
Quantenmechanik und Allgemeine Relativitätstheorie - die beiden triumphalen physikalischen Theorien, die zu Beginn des 20. Jahrhunderts aufkamen - erwiesen sich als inkonsistent. Die Schwierigkeit tritt auf, wenn die als Renormierung bezeichnete Methode angewendet wird. Ich werde über die Renormierung am Beispiel von Photonen und Gravitonen sprechen, über die wir bereits in den vorhergehenden Kapiteln gesprochen haben. Das Wesentliche der Inkonsistenz ist, dass Photonen uns zu einer renormierbaren Theorie führen (was „gute Theorie“ bedeutet), während Gravitonen zu einer nicht normalisierbaren Theorie führen, und dies bedeutet tatsächlich, dass wir keine allgemeine Theorie haben, die Photonen und Gravitonen beschreibt.

Photonen interagieren mit elektrischen Ladungen, sind aber selbst elektrisch neutral. Beispielsweise emittiert ein Elektron mit einer elektrischen Ladung in einem Wasserstoffatom, das von einem Energieniveau zum anderen springt, ein Photon. Genau das meine ich, wenn ich sage, dass Photonen mit Ladungen interagieren. Die Aussage, dass das Photon selbst keine elektrische Ladung hat, ist gleichbedeutend mit der Aussage, dass Licht keine Elektrizität leitet. Wenn dies nicht so wäre, würden Sie jedes Mal einen elektrischen Schlag bekommen, wenn Sie sich an einen Gegenstand klammern, der lange genug im Sonnenlicht gelegen hatte. Photonen interagieren nicht miteinander; Sie interagieren nur mit elektrischen Ladungen.

Gravitonen reagieren nicht auf Ladungen, sondern auf Masse, Energie und Impuls. Und da sie Energie übertragen, interagieren sie auch miteinander. Es mag den Anschein haben, dass dies kein besonderes Problem darstellt, aber gerade deshalb stoßen wir auf Schwierigkeiten. Die Quantenmechanik lehrt uns, dass sich Gravitonen sowohl als Wellen als auch als Teilchen verhalten. Teilchen sind hypothetisch Punktobjekte. Und der Punkt Graviton wird Sie anziehen, je stärker, desto näher kommen Sie ihm. Sein Gravitationsfeld kann als Emission anderer Gravitonen beschrieben werden. Wir werden den Versuch Graviton mütterlich und die von ihm emittierten Gravitonen als Tochter bezeichnen. Das Gravitationsfeld in der Nähe des Muttergravitons ist sehr stark. Die Gravitonen seiner Tochter haben also enorme Energien und Impulse. Dies folgt direkt aus dem Unsicherheitsprinzip: Tochtergravitonen werden in einem sehr kleinen Abstand Δx vom Elterngraviton beobachtet, und daher ist gemäß der Unsicherheitsrelation Δp × Δx ≥ h / 4π ihre Impulsunsicherheit Δp sehr groß. Das Problem ist, dass Gravitonen auch empfindlich auf Impuls reagieren. Die Tochtergravitonen selbst emittieren Gravitonen. Der gesamte Prozess verzweigt sich und divergiert unglaublich schnell: Sie können nicht alle Konsequenzen der Wechselwirkung aller Gravitonen berücksichtigen.

In der Tat passiert etwas Ähnliches in der Nähe des Elektrons. Wenn Sie versuchen, das elektrische Feld sehr nahe am Elektron zu messen, provozieren Sie es, um ein Photon mit einem sehr großen Impuls zu emittieren. Dies scheint harmlos zu sein, da Photonen bekanntlich keine anderen Photonen emittieren. Das Problem ist, dass ein Photon ein Elektron-Positron-Paar hervorbringen kann, das dann noch mehr Photonen emittiert, die neue Elektronen und Positronen erzeugen ... Ein komplettes Durcheinander! Das Erstaunlichste ist, dass man im Fall von Elektronen und Photonen dennoch die ganze Vielzahl von Teilchen, die voneinander kaskadieren, vollständig beschreiben kann. Manchmal sprechen sie über Kleidung oder „Pelzmäntel“ von Nachkommen, in die ein Elektron eingewickelt ist. Physiker verwenden den Begriff „virtuelle Teilchen“, um elektronische Nachkommen zu beschreiben. Die Renormierung ist eine mathematische Methode, mit der Sie all dieses Durcheinander verfolgen können.


Die Idee der Renormierung ist, dass angenommen wird, dass ein "nacktes" Elektron eine unendliche Ladung und unendliche Masse hat, aber sobald wir ein Elektron "kleiden", erhalten seine Ladung und Masse endliche Werte.

Das Problem mit Gravitonen ist, dass wir die sie umgebende Wolke virtueller Gravitonen nicht renormieren können. Die allgemeine Relativitätstheorie - die Gravitationstheorie - ist nicht renormierbar. Dies scheint ein verwirrendes technisches Problem zu sein: Es besteht eine geringe Wahrscheinlichkeit, dass wir das Problem einfach von der falschen Seite betrachten. Es besteht auch eine noch schwächere Chance, dass eine Theorie namens Maximal Supergravity Theory renormierbar wird. Ich und die meisten Stringtheoretiker sind jedoch davon überzeugt, dass es grundlegende Schwierigkeiten gibt, Quantenmechanik und Schwerkraft zu kombinieren.

Nehmen wir nun die Stringtheorie. Die zugrunde liegende Grundannahme ist, dass die Partikel keine Punktpartikel sind. Stattdessen werden Partikel als Schwingungsmoden einer Saite dargestellt. Nach der allgemein anerkannten Idee der Stringtheorie sind Strings Objekte, die unendlich dünn sind, aber eine endliche Länge (in der Größenordnung von 10 bis 34 Metern) haben und in der Art von Gravitonen miteinander interagieren. Stop stop! - Sie protestieren. "Aber führen in diesem Fall die allgemeinen Probleme mit der Wolke virtueller Partikel - in diesem Fall virtuelle Strings - nicht zu der gleichen Unmöglichkeit, den gesamten Interaktionsprozess zu verfolgen, wie im Fall von Gravitonen?" Nein. Die Tatsache, dass Zeichenfolgen keine Punktobjekte sind, beseitigt das beschriebene Problem im Keim. Die Schwierigkeitsquelle bei Gravitonen ist die Annahme, dass sie gemäß dem Begriff „Punktteilchen“ unendlich klein sind. Das Ersetzen von Gravitonen durch vibrierende Saiten glättet die „scharfen Winkel“ ihrer Wechselwirkung miteinander. "An den Fingern" kann dies wie folgt erklärt werden: Wenn das Graviton ein anderes virtuelles Graviton hervorruft, können Sie den Ort und die Zeit, an dem dies geschah, genau angeben. Aber wenn sich die Schnur verzweigt, sieht es aus wie ein Zweig einer Wasserleitung.


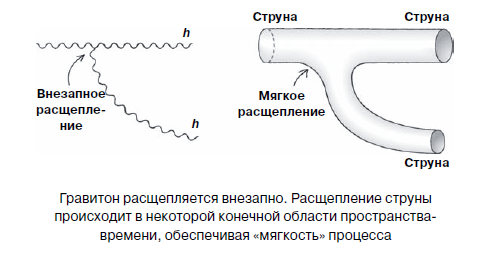
Am Verzweigungspunkt gibt es keinen Punkt, an dem ein Bruch auftritt. Die Y-förmige Figur, die diesen Vorgang darstellt, sieht aus wie ein glattes, durchgehendes Rohrsegment, nur von ungewöhnlicher Form. All dies führt dazu, dass die Teilung der Saite ein "sanfterer" Prozess ist als die Teilung des Partikels. Physiker sagen, dass Strings von Natur aus „sanft“ interagieren, während Teilchen von Natur aus „hart“ interagieren. Es ist diese Weichheit, die hinsichtlich der Anwendbarkeit der quantenmechanischen Beschreibung das beste Verhalten der Stringtheorie als die allgemeine Relativitätstheorie liefert.

Saiten in Raumzeit

Erinnern Sie sich kurz daran, worüber wir über die Vibrationen der Klaviersaite gesprochen haben. Wenn Sie die Schnur zwischen zwei Stiften festziehen und mit einem Hammer darauf schlagen, vibriert sie mit einer bestimmten Frequenz. Die Frequenz ist die Anzahl der Schwingungen pro Sekunde. Zusätzlich zur Hauptfrequenz vibriert die Klaviersaite auch auf Obertönen, dh Vibrationen höherer Frequenzen, die dem Klaviersound eine charakteristische Farbe verleihen. Ich habe diese Analogie bei der Beschreibung des Verhaltens eines Elektrons in einem Wasserstoffatom zitiert: Es hat auch einen fundamentalen Schwingungsmodus, der dem Grundzustand mit minimaler Energie entspricht, und zusätzliche Moden, die höheren Energieniveaus entsprechen.

Die beschriebene Analogie befriedigt Sie möglicherweise nicht vollständig: "Nun, was hat das Elektron im Wasserstoffatom mit der stehenden Welle auf der Klaviersaite zu tun?" - Du fragst. Die meisten sind näher an der Analogie mit dem unendlich kleinen Planeten, der im Orbit um die winzige Sonne kreist - dem Atomkern, nicht wahr? Ist eine solche Analogie gut? Ja und nein. Die Quantenmechanik behauptet, dass die Idee eines Elektrons als Teilchen und die Idee eines Elektrons als Welle so tief miteinander verflochten sind, dass die quantenmechanische Bewegung eines Elektronenteilchens um ein Proton wirklich als stehende Welle beschrieben werden kann.

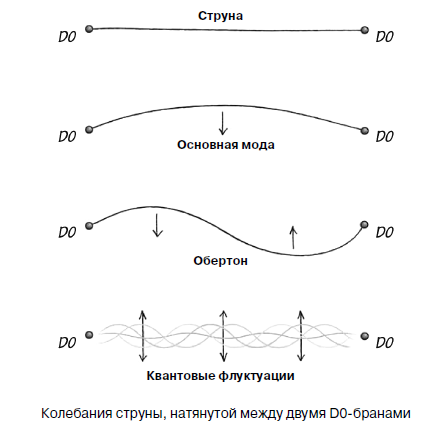
Der Vergleich einer Klaviersaite mit den Saiten, die in der Stringtheorie vorkommen, ist eigentlich eine sehr korrekte Methode. Um Verwechslungen mit verschiedenen Arten von Zeichenfolgen zu vermeiden, werde ich diese Zeichenfolgen, die in der Stringtheorie behandelt werden, als "relativistische Zeichenfolgen" bezeichnen. Dieser Begriff hat eine sehr tiefe didaktische Bedeutung, da die Stringtheorie die Relativitätstheorie umfasst, sowohl spezielle als auch allgemeine. Jetzt möchte ich über eine Konstruktion der Stringtheorie sprechen, die einer Klaviersaite so ähnlich ist, wie eine Saite sogar einer Saite ähneln kann. Relativistische Zeichenfolgen können an Objekten enden, die als D-Branes bezeichnet werden. Wenn wir die mit der Wechselwirkung von Saiten verbundenen Effekte weglassen, können D-Brane als unendlich schwer angesehen werden. Details zu D-Branes werden im nächsten Kapitel besprochen, und jetzt werde ich sozusagen nur einen kleinen Exkurs als „Krücke“ machen. Die einfachste D-Brane heißt D0-Brane (ausgesprochen „De-Zero-Brane“). Dies ist ein Punktteilchen. Ich kann bereits die Empörung einiger Leser über die Rückkehr zu Punktpartikeln hören: "Hat der Autor nicht kürzlich festgestellt, dass die Stringtheorie darauf abzielt, Punktpartikel loszuwerden?" Nun ja, das war bis Mitte der neunziger Jahre, und dann kehrten die Punktteilchen wieder zur Stringtheorie zurück und nicht allein, sondern führten zu einem ganzen Zoo unbekannter Tiere. Aber ich bin mir selbst voraus. Ich möchte nur das saitentheoretische Analogon der Klavierstifte geben, die die Saite in einem angespannten Zustand halten - und die D0-Branes sind in dieser Rolle so geeignet, dass ich nicht widerstehen kann, darüber zu erzählen. Kurz gesagt, wir ziehen die relativistische Saite zwischen zwei D0-Branes, wie eine Klaviersaite zwischen zwei Stiften. Die D0-Brane selbst sind an nichts gebunden, bleiben aber bewegungslos, weil sie eine unendliche Masse haben. Komisch, nicht wahr? Also gut. Über D0-Branes - im nächsten Kapitel und jetzt - nur über eine gespannte Saite.

Das niedrigste Energieniveau einer gedehnten Saite entspricht der Abwesenheit von Vibrationen. Naja ... fast nicht vorhanden, weil immer kleine Quantenschwingungen vorhanden sind und diese Tatsache wichtig ist. Es ist am zutreffendsten, sich das niedrigere Energieniveau als eine kleine Schwingungsenergie im Rahmen dessen vorzustellen, was die Quantenmechanik erlaubt. Die angeregten Pegel einer relativistischen Saite entsprechen ihren Schwingungen entweder bei der Grundfrequenz oder bei Obertönen der Grundfrequenz, und sie kann ebenso wie eine Klaviersaite bei mehreren Frequenzen gleichzeitig schwingen. Aber genau wie ein Elektron in einem Wasserstoffatom kann eine relativistische Kette nicht mit einer beliebigen Frequenz schwingen. Ein Elektron kann Energieniveaus aus einer diskreten Menge auswählen. Relativistische Zeichenfolgen sind genau gleich. Unterschiedliche Schwingungsniveaus haben unterschiedliche Energien, und da Masse und Energie durch die Beziehung E = mc2 in Beziehung stehen, entsprechen unterschiedliche Massen unterschiedlichen Schwingungszuständen.

Es wäre großartig, wenn ich sagen könnte, dass die Schwingungsfrequenz einer Saite durch eine einfache Beziehung vom Typ E = hν mit ihrer Energie zusammenhängt, wie dies bei Photonen der Fall war. Das ist leider nicht so einfach. Die Gesamtmasse der Saite besteht aus mehreren Komponenten. Die erste davon ist die Restmasse der Saite, die der Saitenspannungsenergie zwischen zwei D0-Branen entspricht. Die zweite ist die Masse, die der Schwingungsenergie entspricht, die wiederum aus den Schwingungsenergien aller Obertöne besteht. Denken Sie daran, dass Energie und Masse durch die Beziehung E = mc2 zusammenhängen. Und schließlich ist die dritte Komponente die Masse, die der Energie nicht wiederherstellbarer Quantenfluktuationen entspricht, die als Nullpunktoszillationen bezeichnet werden. Der Begriff „Nullschwingungen“ erinnert uns an die grundsätzliche Unvermeidlichkeit von Quantenfluktuationen. Also: Der Beitrag der Nullpunktsenergie zur Masse der Saite ... ist negativ! Ich stimme zu, das ist seltsam. Sehr seltsam. Um zu zeigen, wie seltsam das ist, werde ich ein Beispiel geben. Wenn wir uns auf einen einzelnen Schwingungsmodus einer Saite beschränken, werden wir sehen, dass die Energie der Nullpunktschwingungen dieses Modus positiv ist. Jeder der höheren Obertöne liefert einzeln einen noch größeren positiven Beitrag zur Saitenenergie. Wenn wir jedoch die Beiträge aller Obertöne angemessen summieren, erhalten wir eine negative Zahl. Wenn Sie denken, dass dies nicht schlimm genug ist, dann sind dies noch schlimmere Nachrichten: Ich habe einen Teil der Wahrheit verborgen, indem ich sagte, dass der Beitrag der Energie von Nullpunktschwingungen negativ ist. Alle diese Effekte - Ruhemasse, Schwingungsenergie und Nullpunktschwingungsenergie - treten in den Ausdruck der Gesamtmasse durch die Quadrate ihrer Werte ein. Und wenn in dieser Summe die Energie der Nullpunktschwingungen vorherrscht, ist das Quadrat der Gesamtmasse negativ, was bedeutet, dass die Masse selbst imaginär ist, wie die Wurzel von minus eins.


Bevor Sie einen solchen Unsinn empört ablehnen, möchte ich hinzufügen, dass in der Stringtheorie eine ganze Reihe von Forschungsarbeiten der Beseitigung des beschriebenen Problems gewidmet ist. Kurz gesagt, das Problem ist, dass das Quadrat der Masse der relativistischen Kette in ihrem niedrigsten Energiezustand negativ ist. Saiten in diesem Zustand werden Tachyonen genannt. Ja, ja, das sind die gleichen Tachyonen, mit denen in jeder Serie die Helden von Star Trek konfrontiert sind. Das sind definitiv schlechte Nachrichten. In dem von mir beschriebenen Modell wäre es möglich, das negative Massenquadrat zu entfernen, indem die D0-Brane, an denen die Enden der Saite befestigt sind, weit genug weggezogen werden, so dass die Spannungsenergie der Saite größer als die Nullpunkt-Vibrationsenergie wird. Wenn sich jedoch keine D0-Branes in der Nähe befinden, bleibt die Saite selbst erhalten. Ohne die Fähigkeit, sich an etwas zu binden, kann es sich selbst einschließen. Jetzt ist sie nicht zwischen etwas und etwas gespannt und kann schwanken, aber vielleicht auch nicht. Das einzige, was sie nicht aufhören kann, ist auf Quantenebene zu schwanken. Und nach wie vor verwandeln Quantenoszillationen eine solche Saite in einen Tachyon, was für die Theorie sehr, sehr schlecht ist. Nach modernen Konzepten sind Tachyonen instabil, sie ähneln einem Bleistift, der auf der Spitze balanciert. Sie können versuchen, einen solchen Stift auszugleichen, aber jeder leichte Atemzug wird ihn umkippen. Die Stringtheorie mit Tachyonen ähnelt einer Theorie, die Millionen von Stiften beschreibt, die auf dem Rand stehen und den Raum füllen.

Ich habe jedoch zu viel übertrieben. Es gibt eine Sparlösung für Tachyonen. Angenommen, der Grundzustand einer Tachyonschnur entspricht der imaginären Masse und ihrem Quadrat: m2 <0. Die Schwingungsenergie leistet auch einen gewissen Beitrag zum Quadrat der Masse. Wenn Sie das richtige Deck verwenden und die Karten auf die erforderliche Weise übergeben, können Sie sicherstellen, dass die Gesamtmasse der Zeichenfolge genau Null ist. Dies ist ermutigend, da es bekanntlich in der realen Welt masselose Teilchen wie Photonen oder Gravitonen gibt. Wenn die Strings wirklich die reale Welt beschreiben, müssen sie daher masselos sein, oder genauer gesagt, zumindest einige der Quantenzustände der Strings müssen masselos sein.

Bitte beachten Sie, dass Sie das richtige Kartenspiel nehmen müssen. Mit dieser Metapher wollte ich sagen, dass wir eine 26-dimensionale Raumzeit brauchen. Sie haben vielleicht schon vermutet, dass alles zu dieser Schande führen wird, also werde ich mich nicht entschuldigen. Es gibt mehrere Argumente für 26 Dimensionen, aber die meisten sind rein mathematisch, und ich befürchte, dass sie der Mehrheit der Leser nicht überzeugend erscheinen werden. Das Argument, das ich geben werde, ist physischer. Wir möchten masselose Quantenzustände von Strings erhalten. Wir wissen, dass Quantennullschwingungen m2 in die negative Richtung „drücken“. Wir wissen auch, dass Schwingungsmoden m2 in die entgegengesetzte Richtung „drücken“. Der minimal mögliche Wert der Schwingungsenergie hängt nicht von der Raumdimension ab, während die Größe der Quantennullschwingungen abhängt. Schauen wir es uns von dieser Seite an: Wenn etwas zögert - eine Klaviersaite oder etwas anderes -, tut es dies in eine bestimmte Richtung. Die Klaviersaite schwingt in die Richtung, in die der Hammer sie getroffen hat. Beispielsweise schwingt eine Klaviersaite auf und ab, jedoch nicht rechts oder links. Das Wackeln wählt eine Richtung und ignoriert den Rest. Im Gegensatz dazu treten quantenmechanische Nullpunktschwingungen in alle möglichen Richtungen auf, und das Hinzufügen jeder neuen Dimension fügt Quantenschwankungen einer anderen Richtung hinzu, in der Schwingungen auftreten können. Mehr mögliche Schwingungsrichtungen oder, wie sie genannt werden, Freiheitsgrade bedeuten eine größere Anzahl von Schwankungen, was zu einem größeren negativen Beitrag zu m2 führt. Es bleibt nur zu berechnen, wie die Beiträge zur Gesamtmasse der Schwingungsmoden und der Nullschwingungen zu wählen sind. Es stellt sich heraus, dass ein Schwingungsmodus mit einem minimalen Energiewert durch eine 26-dimensionale Quantennullschwingung kompensiert wird. Schauen Sie sich das optimistisch an, denn die Anzahl der notwendigen Messungen könnte nicht ganzzahlig sein! Was würden wir zum Beispiel mit 26,5 Dimensionen tun?

Machen Sie sich keine Sorgen, wenn Sie mit verschiedenen Arten von Schwankungen nicht ganz vertraut sind. Sie sind sehr ähnlich. Der einzige Unterschied zwischen Schwingungsmoden und Quantennullschwingungen besteht darin, dass Schwingungsmoden vorhanden sein können oder nicht, während Nullschwingungen immer vorhanden sind. Null Vibrationen sind jene minimalen Bewegungen, deren Vorhandensein nach dem Unsicherheitsprinzip erforderlich ist. Zusätzlich zum Hauptmodus sind in den Schwingungen der Saite Obertöne vorhanden, die der Saite neue quantenmechanische Eigenschaften verleihen. , , . . , . , , -. , . — - .


, : , . , , . . 26- . . , , , . .

, 26 10. , . - . --, , . . -- , « », . , , - ˆ, ˆ. , . - . — . - , .

, . . -, . , , , , . , , , , , , - , , , , . , . , - , , . . . , . — .

»Weitere Informationen zum Buch finden Sie auf der Website des Herausgebers
» Inhalt
» Auszug

20% —