Wir verstehen die Teilchenphysik: 8) wie Teilchen mit Feldern interagieren

Teilchenphysik verstehen:
1. Ball auf einer Feder, Newtonsche Version
2. Eine Quantenkugel auf einer Feder
3. Wellen, klassischer Look
4. Wellen, die klassische Bewegungsgleichung
5. Quantenwellen
6. Felder
7. Teilchen sind Quanten
8. Wie Partikel mit Feldern interagieren

Wie funktioniert das Higgs-Feld:
1. Die Hauptidee

In einem früheren Artikel der Reihe habe ich erklärt, dass Teilchen der Natur Quanten relativistischer Felder sind, die die Bewegungsgleichungen der Klassen 0 und 1 erfüllen. Aber was ich bisher nicht gesagt habe, so ist diese Aussage glücklicherweise nur teilweise wahr. Die realen Gleichungen sind immer etwas komplizierter, so dass die Verbindung von Partikeln und Feldern erhalten bleibt, aber viel vielfältigere Phänomene und Prozesse möglich werden, einschließlich des Auftretens von Partikeln nach der Kollision anderer Partikel, des Zerfalls von Partikeln in andere Partikel und der Streuung von Partikeln voneinander. sowie die Bildung von so interessanten Objekten wie Protonen und Neutronen, Atomkernen und Atomen. Ich werde das alles nicht im Detail erklären können, aber in diesem Artikel werde ich Ihnen eine Einführung geben, wie das alles funktioniert.

Der Hauptunterschied zwischen den Gleichungen, die ich "Klasse 0" und "Klasse 1" nannte, und den Gleichungen, die für die reale Physik von Bedeutung sind, besteht darin, dass es in realen Gleichungen zusätzliche Terme gibt, die von zwei oder mehr Feldern abhängen und nicht nur von einem . Das heißt, anstelle einer Gleichung der Klasse 0 für ein relativistisches Feld Z (x, t), das aussieht

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

Für reale Felder sehen die Gleichungen eher so aus:

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = y'Z (x, t) ^ 3 + yA (x, t) B (x, t)$$

Wenn y und y 'Zahlen sind (normalerweise kleiner als 1), ist Z eine kurze Notation von Z (x, t) und A (x, t) und B (x, t) sind ein Paar anderer Felder. In solchen Gleichungen kann man das Auftreten von Begriffen wie A (x, t) Z (x, t) oder A (x, t) ² Z (x, t) oder Z (x, t) ² oder sogar A erwarten (x, t) d ² Z / dt ² usw. Welche Mitglieder erscheinen können und welche nicht, hängt von den Details der am Prozess beteiligten Felder ab. Die Regeln sind streng, aber ziemlich verwirrend, deshalb werden wir vorerst nicht darauf eingehen. Im Allgemeinen haben wir aus Experimenten festgestellt (und aus theoretischer Sicht verstanden), dass in der Natur:

• Jeder prinzipiell gültige Begriff (Erhaltung der elektrischen Ladung oder Entsprechung der Einsteinschen Relativitätstheorie) erscheint in den Gleichungen,
• Mitglieder mit vielen Feldern sind jedoch normalerweise sehr klein und unbedeutend im Vergleich zu Mitgliedern mit einem, zwei und manchmal drei Feldern (Mitglieder mit Ableitungen von Zeit oder Raum sind normalerweise auch klein).

Daher kann man sich in den interessantesten physikalischen Prozessen auf alle gültigen Begriffe mit einem, zwei oder drei Feldern konzentrieren.

Ein bisschen Terminologie. Die Terme in den Gleichungen mit Feldern werden im ersten Grad als linear bezeichnet. Alle Terme in unseren Gleichungen der Klasse 0 oder 1 waren linear. Elemente mit zwei oder drei Feldern werden als quadratisch oder kubisch bezeichnet. Im Allgemeinen werden sie als nichtlinear bezeichnet. Alle interessanten Phänomene unserer Welt erscheinen aufgrund nichtlinearer Terme in den Bewegungsgleichungen - nämlich der Wechselwirkung von Feldern untereinander und mit sich selbst. Lassen Sie uns einen von ihnen studieren.

Das Entstehen einer neuen Welle aus der Resonanz der beiden anderen

Um eine Vorstellung davon zu bekommen, wie interessant alles werden kann, nehmen wir drei Felder: A (x, t), B (x, t), C (x, t) und eine vereinfachte Situation. Angenommen, die Felder A und B erfüllen ungefähr Gleichungen der Klasse 0 (und enthalten masselose Quanten), und Feld C erfüllt Gleichungen der Klasse 1 (enthält Wellen mit einer Mindestfrequenz ν _min und dementsprechend Quanten mit der Masse m = h ν _min / c ² , wobei h - Planck-Konstante). Wir werden ihren Gleichungen auch nichtlineare Terme hinzufügen. Insbesondere so (der Kürze halber schreiben wir "A" anstelle von "A (x, t)" usw. c ist die Lichtgeschwindigkeit, y ist eine Zahl, die normalerweise kleiner als 1 ist):

$$

$$d ^ 2A / dt ^ 2 - c ^ 2 d ^ 2A / dx ^ 2 = y BC \\ d ^ 2B / dt ^ 2 - c ^ 2 d ^ 2B / dx ^ 2 = y AC \\ d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y AB$$

Kleingedrucktes: Ich habe allen drei Gleichungen nichtlineare Terme hinzugefügt, da das Vorhandensein solcher Terme in einer der Gleichungen und das Fehlen dieser Terme in der anderen zu Widersprüchen führen wird. Beispielsweise wird keine Energie gespart. Für den Prozess, den ich beschreibe, müssen wir nur nichtlineare Terme in den Bewegungsgleichungen von Feld C berücksichtigen.

Lassen Sie uns sehen, was mit einem solchen Satz von Gleichungen passiert, wenn die Welle von Feld A auf die Welle von Feld B trifft. Im Prinzip können wir dies durch Anwendung der Methode der genauen Untersuchung erraten. Wenn sich im Feld A eine Welle befindet, ist A (x, t) in der Nähe ungleich Null. Wenn sich die Wellen der Felder A und B überlappen, wird das Ergebnis der Multiplikation von A (x, t) und B (x, t) ungleich Null. Nun wenden wir uns der Gleichung für C zu: Änderungen im Feld C in Zeit und Raum (zwei Terme auf der linken Seite) sind mit dem Produkt A und B (einer der Terme auf der rechten Seite) verbunden.

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B$$

Selbst wenn das Feld C Null ist, wenn A (x, t) B (x, t) ungleich Null wird, wird C (x, t) im selben Abschnitt bald ungleich Null. Kurz gesagt, infolge des Zusammentreffens der Wellen A und B tritt eine gewisse kleine Störung des Feldes C auf.

Kleingedrucktes: Sie könnten interessiert sein - nachdem C ungleich Null wird, ob der Term A (x, t) C (x, t) in der Bewegungsgleichung für das Feld enthalten ist. Dies führt zu einer zusätzlichen Störung des Feldes B. Die Antwort lautet Ja, aber dieser Effekt wird es tun noch kleiner. Bis wir ihn ignorieren und später herausfinden, warum es sich gelohnt hat, dies zu tun.

In Abb. Abbildung 1 zeigt eine Welle mit einer Frequenz ν in Feld A (grün), die mit einer Frequenzwelle ν in Feld B (blau) auftritt. Ich habe Frequenzen der Einfachheit und Symmetrie halber ausgeglichen. Später werden wir sehen, warum andere Fälle darauf zurückzuführen sind. Die Geschwindigkeit ν kann geschätzt werden, indem die grüne Welle und die vertikale Linie beobachtet werden, die sich an einem Punkt im Raum befinden und mit der Welle schwingen.

Das orangefarbene Produkt unten zeigt das Produkt A (x, t) B (x, t); Es ist zu sehen, dass es ungleich Null wird, wenn zwei Wellen überlagert werden. Es ist auch zu sehen, dass es zeitlich variiert. Sie können sehen (im Vergleich zu einem oszillierenden vertikalen Balken), dass A (x, t) B (x, t) doppelt so schnell schwingt. Denken Sie an diese wichtige Tatsache. Wenn im allgemeinen Fall eine Frequenzwelle ν ₁ auf eine Frequenzwelle ν ₂ trifft, schwingt ihr Produkt mit einer Frequenz ν ₁ + ν ₂ . Und noch etwas: Sie können feststellen, dass sich die AB-Vibrationen nicht nach rechts oder links bewegen, sondern an Ort und Stelle bleiben. Später werden wir sehen, warum dies wichtig ist.


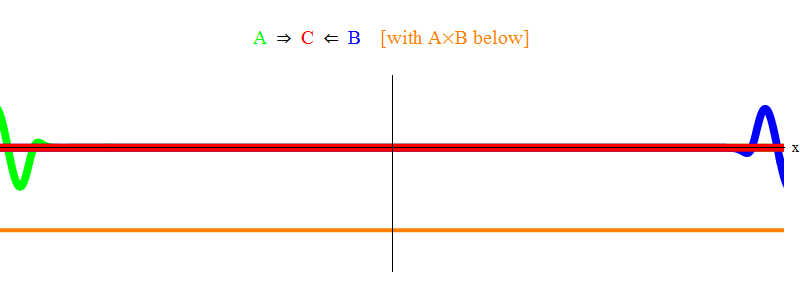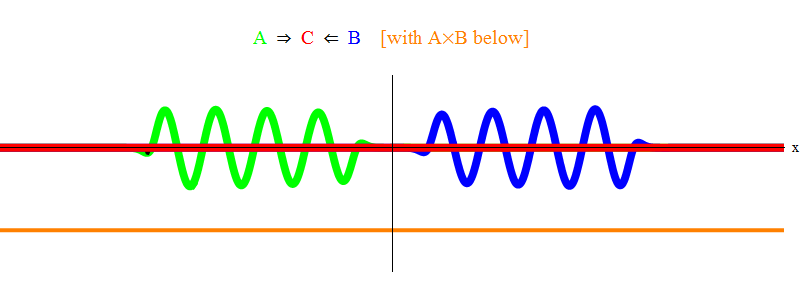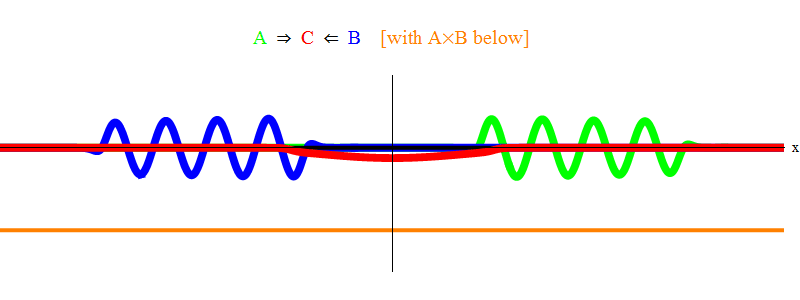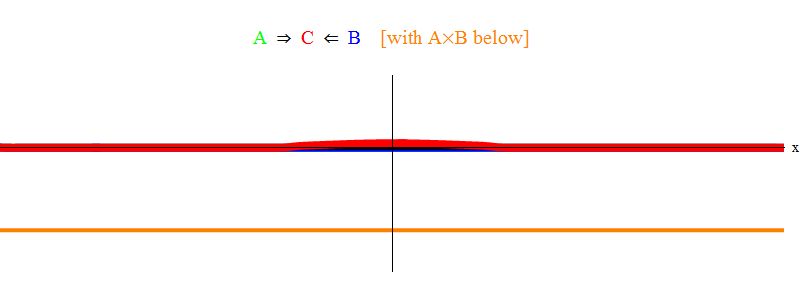Abb. 1

Wie wirkt sich ein Wert ungleich Null von AB auf C aus? Die Antwort hängt stark von der Frequenz ν ab. Zuerst werde ich Ihnen eine Antwort geben und dann eine ungefähre Erklärung des Grundes. Dies ist in der Tat Resonanz . Resonanz ist ein integrales Phänomen aller Schwingungen (Schwingungen), einschließlich Wellen. Ich habe bereits beschrieben, wie der Ball auf der Feder mit einer Eigenfrequenz schwingt und wie die den Ball drückende Schwingungskraft zu Resonanz führen kann, wenn die Schwingungsfrequenz der Kraft mit der Eigenfrequenz des Balls auf der Feder übereinstimmt.

Wenn Sie die Resonanz verstanden haben, werden Sie sehen, dass sich das Feld C, das mit einer minimalen Frequenz und einer horizontalen Geschwindigkeit von Null schwingt, wie eine Kugel auf einer Feder verhält, und AB sich wie eine oszillierende Kraft verhält, die versucht, die Kugel zum Schwingen zu bringen. Daher tritt das Resonanzphänomen auf, wenn die Schwingungsfrequenz AB - 2ν - die minimale Frequenz des Feldes C - ν _{min ist} . Genauer gesagt:

• Wenn 2 ν nicht gleich ν _{min ist} - wenn die Kraft nicht in Resonanz ist -, beginnt C in dem Bereich, in dem AB nicht gleich Null ist, unregelmäßig mit einer kleinen Amplitude zu schwanken.
• Wenn 2 ν = ν _min - wenn die Kraft in Resonanz ist -, schwingt C gleichmäßig mit einer großen Amplitude in dem Bereich, in dem AB ungleich Null ist, und schwankt weiter, selbst wenn AB wieder Null wird.

Abb. 1 zeigt nur die Resonanzsituation 2 ν = ν _min . Es ist zu sehen, dass Welle A beim Durchgang durch Welle B eine stationäre Welle C hinterlässt, die mit einer Frequenz ν _min oszilliert. Kleingedrucktes: in Abb. Es wird eine Skizze gezeigt, keine exakte Lösung der Gleichungen. Die genaue Lösung enthält viele kleine komplexe Funktionen, die die grundlegende physikalische Bedeutung überschatten. Daher habe ich sie aus Gründen der Übersichtlichkeit gelöscht. Später werden wir eine Situation ohne Resonanz betrachten, die viel komplizierter, aber auch für die Physik wichtiger ist.

Die Entstehung eines neuen Teilchens aus der Vernichtung der beiden anderen

Ich habe Ihnen gerade gezeigt, dass die nichtlinearen Terme AB in Gleichung C dazu führen können, dass die Überlagerung der Wellen A und B Schwingungen des Feldes C erzeugt, wenn die Summe der Frequenzen der Felder A und B gleich der Mindestfrequenz des Feldes C ist. Aber was wäre, wenn diese Wellen dies hätten? sehr kleine Amplitude? Was kann passieren, wenn ein Quantum von Feld A auf ein Quantum von Feld B trifft?

• Wenn die Frequenzen AB mit dem Feld C in Resonanz treten, kann ein Quantum des Feldes C auftreten, dh ein reales Teilchen C, und die Quanten A und B verschwinden - „vernichten“.
• Außerdem können sich die Quanten A und B einfach gegenseitig passieren, ohne Teilchen C zu erzeugen.
• Die Gesetze der Quantenmechanik legen nahe, dass die Wahrscheinlichkeit, ein Teilchen C zu erzeugen, proportional zum Quadrat von y ist, das in der Bewegungsgleichung C mit AB multipliziert wird.
• Wenn Frequenzen nicht in die Resonanz eintreten, erscheint das reale Teilchen C nicht. Im Feld C kann jedoch eine vorübergehende Störung auftreten, ein Beispiel für das, was oft als "virtuelles Teilchen" C bezeichnet wird. In diesem Fall können die Quanten A und B verschwinden. Was ist das Ergebnis einer solchen Störung? Ich habe diesen Prozess teilweise am Ende des Artikels im Abschnitt „Schwänze“ beschrieben.

Dies ist der allgemeine Stand der Dinge. Lassen Sie uns in die Details eintauchen.

Was bedeutet für Teilchen, dh Quanten der Felder A, B und C, in Resonanz zu sein oder nicht in Resonanz zu sein? Es sei daran erinnert, dass die Energie eines Quanten aufgrund der Gleichung E = h ν mit seiner Frequenz zusammenhängt. Also übersetzen wir unsere Diskussion über Wellen in eine Diskussion über Teilchen.

Angenommen, unsere Wellen in den Feldern A und B bestehen jeweils aus einem Quanten. Diese Quanten sind masselos, da A und B die Gleichungen der Klasse 0 erfüllen. Genauer gesagt sind die linearen Terme in ihren Bewegungsgleichungen dieselben wie die der Klasse 0. Da die Quanten A und B dieselbe Frequenz haben, haben sie dieselbe Energie, E = h ν. Da der Impuls eines masselosen Quanten p = E / c ist, haben die Quanten A und B Impulse, deren Größe gleich h ν / c ist, deren Richtung jedoch entgegengesetzt ist, da sich einer von ihnen nach links und der andere nach rechts bewegt. Deshalb:

• Die Gesamtenergie zweier Quanten zusammen beträgt 2hν.
• Der Gesamtimpuls der beiden Quanten zusammen ist Null.

Da Energie und Impuls erhalten bleiben, bleibt die Gesamtenergie nach der Kollision zweier Quanten gleich 2hν und das Gesamtmoment bleibt Null.

Im Fall von Wellen haben wir gesehen, dass, da die Gleichung für C einen Term der Form AB enthält, eine Resonanz vorliegt, wenn die Frequenz AB (die als oszillierende Kraft arbeitet) mit der minimalen Frequenz C (die wie eine Kugel auf einer Feder arbeitet) zusammenfällt. Wir übersetzen diese Aussage in Quanten.

Die Frequenz AB beträgt 2 ν, daher ist die Energie der Produkte A und B, wenn die Wellen A und B aus einem Quant bestehen, gleich der Summe der Energien A und B.

$$

$$E_ {AB} = 2 h \ nu = E_A + E_B$$

Die minimale Frequenz C ist gleich ν _min , was bedeutet, dass für ein stationäres Quantum des Feldes C der Impuls 0 und die Energie ist

$$

$$E_C = h \ nu_ {min} = mc ^ 2$$

Wobei m die Masse von Quantum C ist.

Für die Resonanz sind 2 ν = ν _min erforderlich, dh:

$$

$$E_A + E_B = 2 h \ nu = h \ nu_ {min} = mc ^ 2 = E_C$$

Kurz gesagt, Resonanz tritt auf, wenn die Summen gleicher Energien der Teilchen A und B (in unserem Fall sind die Impulse gleich groß und entgegengesetzt gerichtet) gerade ausreichen, um ein stationäres Teilchen C zu erzeugen! Dabei werden die Partikel A und B vernichtet - ihre Energie fließt vollständig in die Erzeugung von Partikel C. Dies ist (schematisch) in Abb. 1 dargestellt. 2, die Sie mit Abb. Vergleichen müssen. 1.


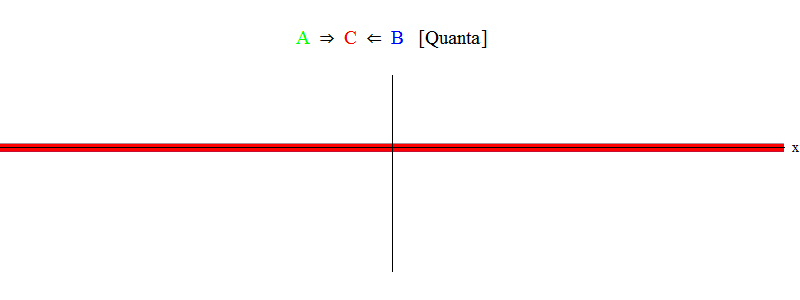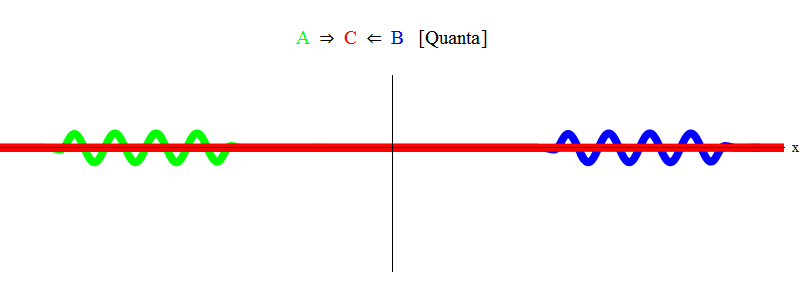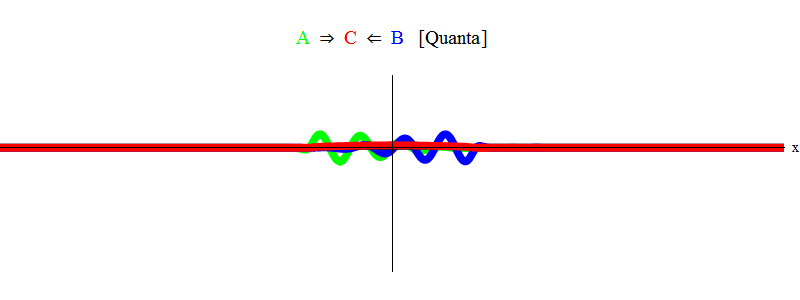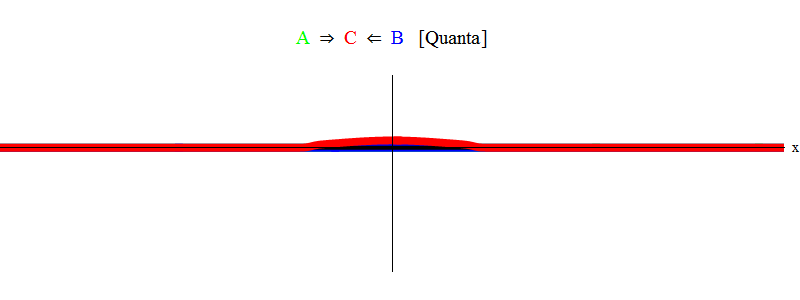Abb. 2

Argumentation

Ich habe Ihnen gerade den Prozess A + B → C gezeigt. In meiner Erklärung habe ich drei verschiedene Arten von Partikeln verwendet, um Verwirrung zu vermeiden. Dieselbe Idee erlaubt es jedoch, Prozesse der Form A + A → C (zum Beispiel Gluon + Gluon → das Higgs-Teilchen, und im Grunde wird das Higgs-Teilchen im Large Hadron Collider erhalten) und Prozesse der Form A + A * → C zu durchlaufen, wobei A * - Antiteilchen für A (zum Beispiel Quark + Antiquark → Z-Teilchen, und so werden Z-Teilchen normalerweise auf dem LHC erhalten). Es ist nur notwendig, kleinere Details zu ändern, aber das Wesentliche bleibt gleich.

Ein weiterer Prozess, der dieselbe Idee darstellt und nur zeitlich umgekehrt ist - der Zerfall von Partikeln. Der Zerfall eines Higgs-Teilchens in zwei Photonen oder Z-Teilchen in einen Quark und einen Antiquark erfolgt im Wesentlichen als Animation in Abb. 2, in die entgegengesetzte Richtung gehen.

Schwänze

1. Wenn der Term AB das Feld C ohne Resonanz stört - wenn 2 ν ≠ ν _min - was passiert dann? Sie können sich daran erinnern, dass Sie eine ungleichmäßige Vibration mit einer kleinen Amplitude erhalten, wenn Sie den Schwung mit dem Kind mit der falschen Frequenz drücken oder eine Kraft auf den Ball auf die Feder ausüben, die mit einer Frequenz schwingt, die nicht mit der Eigenfrequenz der Vibrationen übereinstimmt. Im aktuellen Kontext passiert dasselbe mit Feld C. Feld C wird sich irgendwie verhalten, aber dies wird nicht zum Auftreten eines sich gut verhaltenden Quanten C führen. Es wird nur ein wenig besorgt. Diese schlechte Empörung ist ein Beispiel für die sogenannte "Virtuelle Teilchen C" - aber dies ist trotz seines Namens kein Teilchen (Quantum einer Welle des Feldes C). Seine Masse unterscheidet sich von der Masse des Teilchens C; es kann größer oder kleiner sein. Im Gegensatz zu Partikel C existiert es lange Zeit nicht für sich. Und es erfüllt nicht die Amplitudenbedingungen, die echte Quanten erfüllen müssen. Im Gegensatz zu Teilchen C, das seit einiger Zeit existiert, mit Abb. In 2 existiert eine nichtresonante Störung nur dann, wenn A B schneidet.

Dies bedeutet jedoch nicht, dass es nichts beeinflusst. Beispielsweise können die Partikel A und B voneinander abprallen.

$$

$$A_ \ rechter Pfeil + B_ \ linker Pfeil → C_ {Empörung} → A_ \ linker Pfeil + B_ \ rechter Pfeil$$

Im dreidimensionalen Raum kann ein Rückprall oder eine Streuung im Allgemeinen dazu führen, dass sich A in eine beliebige Richtung und B in die entgegengesetzte Richtung bewegt. Beispiele für solche Prozesse umfassen Elektronen- und Positronenstreuung aufgrund eines virtuellen Photons oder Quark- und Antiquarkstreuung aufgrund eines virtuellen Gluons.

In Gegenwart anderer Felder interagieren D und E mit C und nehmen an der Bewegungsgleichung C teil

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B + y ’D E$$

Viel interessantere Prozesse können auftreten:

A + B → C _Störung → D + E.

Das ist richtig: Partikel A und B können sich dank des virtuellen Partikels C vernichten und zum Auftreten neuer Partikel D und E führen. Dies ist der zweite Weg, um neue Partikel zu erzeugen! Zum Beispiel kann ein Elektron mit einem Positron kollidieren, durch ein virtuelles Photon vernichten (denken Sie daran, dass dies „durch eine Störung des Photonenfeldes bei einer Frequenz bedeutet, die nicht mit der Resonanz übereinstimmt“) und sich in ein Myon und Antimuon oder Quark und Antiquark verwandeln. Der untere Quark und der obere Antiquark können kollidieren, durch ein virtuelles W-Teilchen vernichten und sich in ein Elektron und ein Antineutrino verwandeln. Oder zwei Gluonen können kollidieren, durch ein virtuelles Gluon vernichten und sich in einen oberen Quark und einen oberen Antiquark verwandeln (dies ist der häufigste Weg, um obere Quarks auf einem LHC zu erhalten).

2. Was ist, wenn zwei Wellen in den Feldern A und B unterschiedliche Frequenzen haben, ν _A und ν _B ? Bei geeigneten Frequenzen können Partikel C immer noch auftreten, aber die Resonanzbedingungen sind unterschiedlich und das erzeugte Partikel C ist nicht stationär. Lass es uns herausfinden.

Wenn sie unterschiedliche Frequenzen haben, haben zwei kollidierende masselose Quanten

• Verschiedene Energien $$$E_A = h \ nu_A$ und $$$E_B = h \ nu_B$
• Verschiedene Impulse $$$p_A = + h \ nu_A / c$ und $$$p_B = - h \ nu_B / c$ (hier bedeutet plus rechts, minus links).

Der Gesamtimpuls p _A + p _{B ist} jetzt ungleich Null. Aber die Dynamik bleibt bestehen. Wenn Teilchen C als Ergebnis der Vernichtung der Teilchen A und B auftreten kann, hat es daher einen Impuls p _C = p _A + p _B , so dass es sich nach links oder rechts bewegt und nicht stillsteht. Wenn ν _A > ν _{B ist} , bewegt es sich nach rechts, andernfalls nach links.

Wie viel Energie wird benötigt, um ein sich bewegendes Teilchen C zu erzeugen? Dafür wird mehr Energie benötigt als für ein stationäres - wie jedes massive Teilchen müssen seine Energie und sein Impuls befriedigen

$$

$$E_C ^ 2 = (p_Cc) ^ 2 + (mc ^ 2) ^ 2$$

Dies bedeutet, dass E _C = mc ^{2 ist,} wenn p _C = 0 ist, oder mehr, wenn der Impuls ungleich Null ist. Das Gesetz der Energie- und Impulserhaltung besagt:

$$

$$E_C = E_A + E_B$$

$$

$$p_C = p_A + p_B = E_A / c - E_B / c$$

Woher habe ich die letzte Gleichung? Für ein masseloses Teilchen, p = E / c, und für unsere kollidierenden Teilchen A und B sind ihre Impulse entgegengesetzt, so dass sie sich im Vorzeichen unterscheiden. Ersetzen Sie dies in der vorherigen Gleichung und erhalten Sie:

$$

$$(E_A + E_B) ^ 2 = (E_A - E_B) ^ 2 + (mc ^ 2) ^ 2$$

Die Terme E _A ² und E _B ² werden gegenseitig vernichtet, und wenn wir die Terme E _A E _B nach links verschieben, erhalten wir:

$$

$$4 E_A E_B = (mc ^ 2) ^ 2$$

Durch Teilen durch h ² und Verwenden der Beziehung m = hν _min / c ² erhalten wir die Resonanzbedingung:

$$

$$(2 \ nu A) (2 \ nu B) = \ nu_ {min} ^ 2$$

Was sich korrekt reduziert, wenn ν _A = ν _B auf die Gleichung für ein bewegungsloses Teilchen C, 2 ν = ν _min . Wenn diese Bedingung nicht erfüllt ist, kann Partikel C nicht erzeugt werden. Wenn zufrieden, dann ist es möglich.

3. Ich habe festgestellt, dass die Bewegungsgleichung für Feld C den Term AB enthält, so dass die Gleichung für B den Term AC enthält. Erinnern Sie sich an diese Gleichungen:

$$

$$d ^ 2B / dt ^ 2 - c ^ 2 d ^ 2B / dx ^ 2 = y A C$$

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B$$

Wenn also die Überlagerung der Wellen A und B zum Auftreten einer Welle im Feld C führt, wird sie ungleich Null, wie in Abb. 1, müssen wir uns Sorgen machen, dass sich diese neue Welle C mit der vorhandenen Welle A überlappt und zu einer Änderung des Feldes B führt? Ich antwortete: "Ja, aber wir können das vernachlässigen." Wir können aus einer Kombination von zwei Gründen vernachlässigen.

Erstens aufgrund der Zahl "y", die vor den Multiplikationen von AB und BC erscheint. Die Auswirkung auf das Feld C des Elements AB ist proportional zu y mal A multipliziert mit B. Die Auswirkung auf das Feld B des Elements AC ist auch proportional zu y mal A multipliziert mit C, aber dies ist wiederum gleich y ² mal A multipliziert mit mit A multipliziert mit B. Während also y kleiner als 1 ist, ist y ² kleiner als y, so dass die Auswirkung des AC-Elements auf B im Vergleich zur Auswirkung des AB-Elements auf C gering ist - zumindest für kleine Wellen A und B. In der Praxis sind dies diese Die Wellen sind normalerweise klein: Teilchen A ist ein Quantum der Welle in Feld A, daher hat Welle A kleine Amplituden d.

Daraus folgt ein zweiter, seltsamer, aber überzeugenderer Grund: Wir haben gesehen, dass, wenn ein Quantum A auf ein Quantum B trifft und sich in ein Quantum C verwandelt, die Wellen A und B verschwinden (vernichten). Nach der Erzeugung von C gibt es keine Welle A mehr, daher ist der Wechselstrom Null, dh es gibt keine Auswirkung auf das Feld B.

Und der letzte Haken: Obwohl ich dies ohne zusätzliche Berechnungen nicht beweisen kann, auch wenn A- und B-Wellen aus einem Quant bestehen, wie in Abb. 2, dann der Prozess in Fig. 2 wäre viel komplizierter, wenn y viel größer als 1 wäre. Die Einfachheit der Geschichte, die ich erzählte, erfordert also kleine Werte von y. In der Natur ist die Mehrheit der nichtlinearen Terme in der Teilchenphysik normalerweise klein, daher gilt das, was ich gesagt habe, für die praktischsten Situationen. Die Ausnahmen sind sehr interessant - sie führen zur Erzeugung so komplexer Objekte wie Protonen und anderer Hadronen.