Das Buch „Absolutes Minimum. Wie die Quantentheorie unsere Welt erklärt. “

Die Physik ist die komplexeste komplexe Wissenschaft, sie ist ebenso komplex und faszinierend. Wenn wir die mathematische Komponente verwerfen, wird die Physik sofort jedem zugänglich, der neugierig und einfallsreich ist. Wir werden das Konzept der Gravitationstheorie leicht verstehen und auf komplexe mathematische Gleichungen verzichten. Daher an alle, die darüber nachdenken, was Blaubeeren blau und Erdbeeren rot macht; wer bezweifelt, dass sich Schall in Form von Wellen ausbreitet; Wer sich fragt, warum sich das Verhalten von Licht von jedem anderen Phänomen im Universum unterscheidet, muss verstehen, dass sich das Ganze in der Quantenphysik befindet.

Dieses Buch präsentiert (und entmystifiziert) für gewöhnliche Menschen die magische Welt der Quantenwissenschaft wie kein anderes Buch. Sie spricht über grundlegende wissenschaftliche Konzepte, von Lichtteilchen über Materiezustände bis hin zu den Ursachen der negativen Auswirkungen von Treibhausgasen, und enthüllt jedes Thema ohne die Verwendung spezifischer wissenschaftlicher Begriffe - Beispiele aus dem normalen Alltag. Natürlich kann ein Buch über Quantenphysik nicht ohne ein Minimum an Formeln und Gleichungen auskommen, aber dies ist ein notwendiges Minimum, das für die meisten Leser verständlich ist. Laut dem Autor sollte ein Buch, das die Wissenschaft populär macht, zugänglich sein, aber nicht auf der Ebene des Lesers, sondern um seinen Intellekt und sein allgemeines kulturelles Niveau zu erhöhen und zu entwickeln.

Quanten-Racquetball und Fruchtfarbe

Eine Schlüsseleigenschaft von an Atome und Moleküle gebundenen Elektronen ist, dass ihre Energiezustände diskret sind. Wir sagen, dass die Energie eines Elektrons quantisiert werden kann, dh ein an ein Atom oder Molekül gebundenes Elektron kann nur bestimmte Energiewerte haben. Die Energie ändert sich schrittweise und diese Schritte haben bestimmte diskrete Größen. Energiezustände sind wie Treppen. Sie können auf einer Stufe stehen oder zur nächsten, höheren Stufe aufsteigen. Es ist jedoch unmöglich, auf halbem Weg zwischen den beiden Stufen zu stehen. Diese diskreten oder quantisierten Energiewerte werden oft als Energieniveaus bezeichnet. Im Gegensatz zu normalen Treppen sind die Intervalle zwischen den Energieniveaus normalerweise nicht gleich.

Ein wichtiges Gebiet der modernen Quantenforschung ist die Berechnung der elektronischen Zustände von Molekülen. Dieser Bereich wird Quantenchemie genannt. Solche Berechnungen ermöglichen es, quantisierte Energieniveaus für Elektronen in Molekülen (Energieniveaus) zu erhalten sowie die Struktur von Molekülen zu berechnen. Die Berechnung der Struktur des Moleküls ergibt den Abstand zwischen den Atomen und den Positionen aller Atome im Molekül mit einer Genauigkeit, die nur durch das Unsicherheitsprinzip begrenzt ist. Quantenmechanische Berechnungen ermöglichen es somit, die Größe und Form von Molekülen zu bestimmen. Solche Berechnungen sind wichtig, um die Grundprinzipien der Bindung von Atomen an Moleküle zu verstehen und neue Moleküle aufzubauen. Mit der Entwicklung der Quantentheorie und der Entstehung immer leistungsfähigerer und komplexer Computer, die mühsame mathematische Probleme lösen können, können immer mehr große Moleküle mit den Methoden der Quantenchemie untersucht werden. Eine der wichtigsten Anwendungen der Quantentheorie ist die Entwicklung von Pharmazeutika. Moleküle können so konstruiert werden, dass sie die gewünschte Größe haben und in der Form an bestimmte Orte von Proteinen oder Enzymen „passen“.

Die Quantenchemie erfordert sehr mühsame Berechnungen. Selbst für das einfachste Wasserstoffatom sind quantenmechanische Berechnungen mathematisch sehr kompliziert. Ein Wasserstoffatom besteht aus einem Elektron, das an ein Proton gebunden ist. Ein Proton, das der Kern eines Wasserstoffatoms ist, ist ein positiv geladenes Teilchen und ein Elektron ist negativ geladen. Die Anziehung eines negativ geladenen Elektrons an ein positiv geladenes Proton hält sie zusammen und hält das Wasserstoffatom zusammen. Details zur Berechnung der Energieniveaus des Wasserstoffatoms werden hier nicht vorgestellt, aber in den folgenden Kapiteln werden wir einige Merkmale der Ergebnisse dieser Berechnungen betrachten. Sie geben die Energieniveaus des Wasserstoffatoms und seine Wellenfunktionen an. Es sind Wellenfunktionen, dh Wahrscheinlichkeitsamplitudenwellen für ein Wasserstoffatom, die den Ausgangspunkt für das Verständnis aller Atome und Moleküle bilden. Atome und Moleküle sind komplex, weil sie absolut kleine dreidimensionale Systeme sind, und es muss berücksichtigt werden, wie Protonen und Elektronen miteinander interagieren.

Ein Partikel in einer Box - ein klassischer Fall

Es gibt eine sehr einfache Aufgabe in Bezug auf unser Thema. Es ist als Partikelproblem in einer Box bekannt. Es erfordert keine komplizierte Mathematik, um es zu lösen, aber diese Lösung ermöglicht es uns, wichtige Eigenschaften gebundener Elektronen zu veranschaulichen, beispielsweise die Quantisierung von Energieniveaus und die wellenartige Natur von Elektronen in gebundenen Zuständen. Bevor wir die Natur des Elektrons in einer eindimensionalen Box mit Atomgrößen analysieren, diskutieren wir das klassische Problem eines idealen eindimensionalen Spielplatzes für Racquetball, um die Unterschiede zwischen dem klassischen (großen) und dem quantenmechanischen (absolut kleinen) System zu identifizieren.

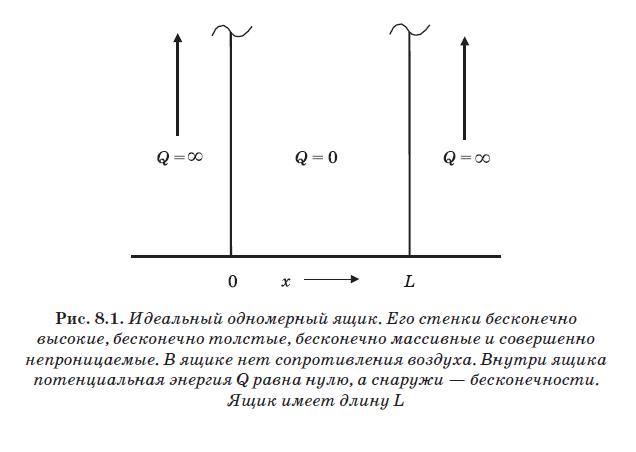
In Abb. 8.1 zeigt die perfekte "Box". Er ist eindimensional. Seine Wände gelten als unendlich hoch, unendlich massiv und völlig undurchdringlich. In der Box befindet sich keine Luft, die einer Bewegung widersteht. In der Figur ist das Innere der Box mit Q = 0 und das Äußere mit Q = ∞ bezeichnet. Es wurde früher gesagt, dass ein Teilchen als frei bezeichnet wird, auf das keine Kraft einwirkt. Kräfte entstehen, wenn ein Teilchen mit etwas interagiert. Beispielsweise kann ein negativ geladenes Teilchen wie ein Elektron mit einem positiv geladenen Proton interagieren. Die Wechselwirkung in Form einer Anziehung zwischen entgegengesetzt geladenen Teilchen erzeugt eine auf das Elektron wirkende Kraft. Bei der Steuerung von Elektronen in einer CRT (siehe Abb. 7.3) erzeugt ein elektrisches Feld eine Kraft, die auf die Elektronen wirkt und sie zwingt, ihre Richtung zu ändern.

Ein Maß für die Wechselwirkung eines Teilchens mit etwas, das es beeinflusst, wie beispielsweise einem elektrischen Feld, wird als Potential bezeichnet und hat die Dimension Energie. In Zukunft wird das Potential mit dem Buchstaben Q bezeichnet. In der Box ist Q = 0, wie im Fall eines freien Teilchens. Dies bedeutet, dass das Partikel mit nichts in der Box interagiert. Es gibt keine elektrischen Felder oder Luftwiderstände. Außerhalb des Kastens ist jedoch Q = ∞. Unendliches Potential bedeutet, dass ein Teilchen unendliche Energie haben müsste, um sich in Bereichen außerhalb des Kastens zu befinden. Der Ausdruck Q = ∞ ist nur eine Möglichkeit, die Aussage zu formalisieren, dass die Wände der Box ideal sind. Ein Teilchen kann keine Wände durchdringen oder darüber springen, egal wie groß seine Energie ist. Wenn Sie ein Partikel in eine solche Schachtel geben, kann es nicht abrutschen und bleibt immer darin. In diesem Sinne ist das Partikel in einer Box eingeschlossen. Es kann sich in einem Raumbereich der Länge L befinden, aber nirgendwo anders.

In Abb. Abbildung 8.2 zeigt einen Ball zum Spielen von Racquetball, der von den Wänden eines idealen eindimensionalen klassischen (großen) Racquetballplatzes abprallt. Wie bereits erwähnt, sind diese Wände ideal, aber es gibt keinen Luftwiderstand im Inneren. Darüber hinaus ist der Ball auch ideal, dh er hat absolute Elastizität. Wenn der Ball mit der Wand kollidiert, zieht er sich wie eine Feder zusammen und richtet sich wieder auf, wodurch er abprallt. Echte Bälle sind nicht perfekt elastisch. Wenn der Ball beim Aufprall zusammengedrückt wird, wird nicht die gesamte Energie, die beim Zusammendrücken aufgewendet wird, von der Wand abgestoßen. Ein Teil der Energie, die für das Komprimieren des Balls aufgewendet wird, wird zum Erhitzen verwendet. Hier betrachten wir den Ball jedoch als perfekt elastisch. Wenn Sie gegen eine Wand schlagen, wird die gesamte kinetische Energie des Balls, die ihn komprimiert, darauf verwendet, den Ball von der Wand wegzuschieben. Daher ist die Geschwindigkeit des Balls unmittelbar vor der Kollision mit der Wand gleich der Geschwindigkeit seines Rückpralls nach der Kollision.

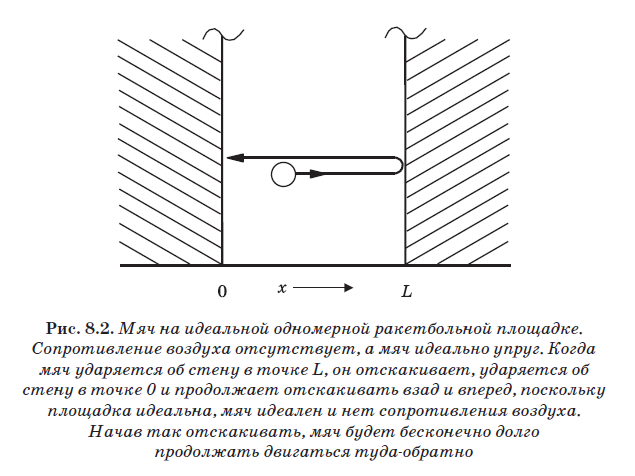
Auf diesem idealen Racquetballplatz springt der Ball ohne Energieverlust von den Wänden. Außerdem gibt es weder Luftwiderstand noch Schwerkraft. Daher bewegt sich der Ball immer hin und her und reflektiert sich von den Wänden. Es trifft an Punkt L auf die Wand, prallt ab, kollidiert an Punkt 0 mit der Wand, springt erneut und bewegt sich weiter hin und her. Da das Potential in der Box Null ist (siehe Abb. 8.1), wirken keine Kräfte auf die Kugel. Daher ist seine Energie rein kinetisch:

Dabei ist m die Masse des Balls und V seine Geschwindigkeit. Wenn der Ball schwachen äußeren Einflüssen ausgesetzt ist, wird seine Geschwindigkeit etwas niedriger und der Ek-Wert nimmt ebenfalls leicht ab. In diesem idealen Racquetball kann sich die Energie kontinuierlich ändern. Der Wert von Ek kann willkürlich erhöht oder verringert werden, abhängig nur von der Stärke des Aufpralls auf den Ball.

Ein weiteres wichtiges Merkmal des klassischen Racquetballs ist die Fähigkeit, den Ball so anzuhalten, dass er bewegungslos auf dem Boden liegt. In dieser Situation ist seine Geschwindigkeit Null: V = 0. Und da V = 0, dann Ek = 0. Bei V = 0 ist der Impuls ebenfalls Null, da p = mV, so dass wir den Impuls genau kennen. Liegt der Ball auf dem Boden (V = 0), ist seine Position bekannt. Wenn wir diese Position x bezeichnen (siehe Abb. 8.2), liegt der Wert von x im Bereich von 0 bis L. Der Wert von x kann keine anderen Werte annehmen, da sich der Ball auf dem Spielfeld (in der Box) befindet und nicht außerhalb von liegen kann für perfekte Wände. Der Ball kann in einer bestimmten Position x auf dem Boden des Spielfelds platziert werden, und dann ist seine Position sicher bekannt. Dies ist eine Eigenschaft eines makroskopischen Spielplatzes, auch ideal. Dies ist ein klassisches System, in dem man den Impuls p und die Position x genau und gleichzeitig kennen kann.

Der Racquetballplatz hat eine Länge von 12 m, einen Durchmesser von 5,6 cm und ein Gewicht von etwa 0,04 kg. Offensichtlich wird das Racquetballspiel von der klassischen Mechanik beschrieben. Mit Hilfe von Licht können Sie dem Abprallen des Balls hin und her folgen, ohne ihn zu beeinflussen.

Teilchen in einer Schachtel - Quantenkoffer

Was wird sich ändern, wenn wir uns nun der Betrachtung des Quanten-Racquetball zuwenden? Der Standort bleibt ideal, aber jetzt beträgt seine Länge nicht 12 m, sondern 1 nm (10–9 m). Zusätzlich hat das Teilchen eine Elektronenmasse von 9,1 10–31 kg und nicht 0,04 kg. Dies ist also das Problem eines Quantenteilchens in einer Box.

Wir können sofort sagen, dass die kleinste Energie eines Quantenteilchens in einer nanometergroßen Box nicht Null sein kann. Auf einem klassischen Racquetballfeld ist die Ballgeschwindigkeit V möglich, die gleich Null ist, was bedeutet, dass der Impuls p = mV auch Null sein kann. Zusätzlich hat die Position der Kugel x eine klar definierte Bedeutung. Zum Beispiel kann der Ball genau in der Mitte des Spielfelds still liegen (V = 0), was x = L / 2 entspricht. In diesem Fall ist für unseren klassischen Racquetball ∆p = 0 und ∆x = 0. Der Wert des Produkts ∆x∆p = 0 entspricht nicht dem Heisenbergschen Unsicherheitsprinzip, was normal ist, da es sich um das klassische System handelt. Ein absolut kleines Teilchen in einer nanometergroßen Box ist jedoch ein Quantenobjekt und muss dem Unsicherheitsprinzip folgen, das besagt, dass ∆x∆p ≥ h / 4 ist. Wenn V = 0 und x = L / 2, dann kennen wir sowohl x als auch p, was bedeutet, dass ∆x∆p = 0 ist, wie beim klassischen Racquetball. Für ein Quantensystem ist dies nicht möglich. Somit kann V nicht gleich Null sein. Ein Teilchen kann an einem bestimmten Punkt nicht bewegungslos bleiben. Und wenn der Wert von V ungleich Null ist, kann der Wert von Ek nicht gleich Null sein. Das Unsicherheitsprinzip besagt, dass die kleinste Energie unseres Quanten-Racquetballs nicht Null sein kann. Ein Quantenball bleibt niemals bewegungslos.

Quantenpartikel-Energiewerte in einer Box

Welche Energie kann ein Quantenteilchen in einer nanometergroßen Box haben? Diese Frage kann ohne komplizierte Berechnungen beantwortet werden, aber zuerst müssen wir wieder zu den Wellen zurückkehren. In Kapitel 6 haben wir über die Wellenfunktionen freier Teilchen gesprochen. Die Wellenfunktion eines freien Teilchens mit einem bestimmten Impuls p ist eine Welle, die sich über den Raum erstreckt. Ein Elektron mit einem perfekt definierten Impuls ist also eine delokalisierte Welle, die den gesamten Raum bedeckt. Die Wahrscheinlichkeit, ein freies Elektron zu detektieren, ist überall gleich. Ein solches Elektron hat eine genau definierte kinetische Energie Ek = 1 / 2mV2, da es einen genau definierten Impuls p = mV hat.

Das Elektron in der Nanometerbox ähnelt unserem freien Teilchen in Bezug auf den inneren Bereich der Box, in dem Q = 0. Es gibt kein Potential in der Box und daher wirken keine Kräfte auf das Teilchen. In dieser Hinsicht ist es einem freien Teilchen sehr ähnlich, auf das auch keine Kräfte wirken. Es gibt jedoch einen wichtigen Unterschied zwischen dem Partikel in der Box und dem freien Partikel - dies sind die Wände der Box. Das Elektron in der Box befindet sich nur in der Box. Die ideale Natur der Box erlaubt es nicht, dass sich ihre Wellenfunktion auf den gesamten Raum ausbreitet. Das Partikel befindet sich in der Box und kann niemals außerhalb sein. Die Wellenfunktion legt die Amplitude der Wahrscheinlichkeit fest, ein Teilchen in einem bestimmten Raumbereich zu erfassen. Dies ist eine Born-Interpretation der Wellenfunktion. Wenn unser Elektron nur innerhalb der Box und niemals außerhalb detektiert werden kann, sollte die Wahrscheinlichkeit seiner Detektion in der Box endlich und außerhalb von Null sein. Wenn die Wahrscheinlichkeit, ein Teilchen außerhalb der Box zu finden, Null ist, muss die Wellenfunktion an allen Punkten außerhalb der Box Null sein.

Wir sind also zu dem Schluss gekommen, dass die Wellenfunktion eines Partikels in einer Box der Wellenfunktion eines freien Partikels ähnlich ist, die Wellenfunktion jedoch außerhalb der Box Null sein muss. In seiner Interpretation der Natur der quantenmechanischen Wellenfunktion hat Born der Form, die die Wellenfunktion annehmen kann, einige physikalische Einschränkungen auferlegt. Eine davon ist, dass eine gute Wellenfunktion kontinuierlich sein muss. Diese Bedingung bedeutet, dass sich die Wellenfunktion von Ort zu Ort reibungslos ändern muss. Eine unendlich kleine Positionsänderung kann nicht zu einem unerwarteten Wahrscheinlichkeitssprung führen. Dies ist ein sehr einfacher Gedanke. Wenn die Wahrscheinlichkeit, ein Partikel in einem sehr kleinen Raumbereich zu erfassen, beispielsweise 1% beträgt, kann eine Verschiebung eines unvorstellbar kleinen Werts die Wahrscheinlichkeit, ein Partikel zu erfassen, nicht plötzlich auf 50% bringen. Dies geht aus den Bildern der Wellenpakete in Fig. 1 hervor. 6.7. Die Wahrscheinlichkeit variiert reibungslos von Ort zu Ort. Dies ermöglicht es uns, der Beschreibung der Wellenfunktionen eines Teilchens in einer Box etwas hinzuzufügen, zusätzlich zu der Tatsache, dass es sich um Wellen mit endlichen Amplituden innerhalb der Box und einer Amplitude von Null außerhalb handelt. Da die Wellenfunktion stetig sein muss, muss sie von innen direkt an der Kastenwand eine Amplitude von Null haben, damit sie mit der Amplitude von Null der Wellenfunktion außerhalb der Box übereinstimmt.

In Abb. Abbildung 8.3 zeigt die (verbotene) Diskontinuität der Wellenfunktion innerhalb der Box. Die Wellenfunktion wird angezeigt (griechischer Buchstabe "fi"). Die vertikale Achse repräsentiert die Amplitude der Wellenfunktion. Die gestrichelte Linie zeigt den Nullpegel an. Wellenfunktionen, bei denen es sich um Wellen mit Wahrscheinlichkeitsamplitude handelt, können zwischen positiven und negativen Werten schwanken. Die in Abb. 8.3 hat in der Nähe der Wände andere Werte als 0. Die Wellenfunktion muss jedoch außerhalb des Rahmens Null sein, dh für Werte von x kleiner als 0 und größer als L muss sie Null sein. In der Abbildung springt die Wellenfunktion unerwartet von einem Wert ungleich Null in der Nähe der Wand innerhalb der Box zu einem Nullwert unmittelbar hinter der Wand außerhalb der Box. Somit ist die in Fig. 1 gezeigte Wellenfunktion 8.3 ist ungültig, da es nicht kontinuierlich ist. Diese Funktion kann kein Quantenteilchen in einer Box darstellen.

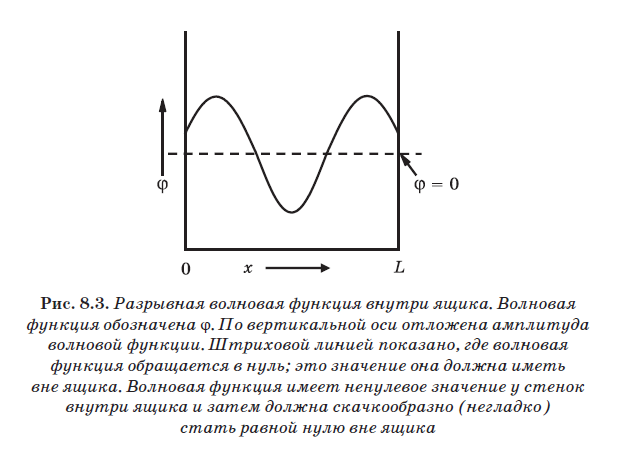
Die Wellenfunktion muss an den Wänden einen Nullwert haben

Damit die Wellenfunktionen, die das Teilchen in der Box darstellen, physikalisch akzeptabel sind, müssen ihre Werte an den Wänden Null sein, und dann treten keine Lücken an den Wänden auf. Es ist nicht schwer, diese Bedingung zu erfüllen. Die Wellenfunktion schwankt zwischen positiven und negativen Werten. Jedes Mal, wenn von positiven zu negativen Werten oder von negativen zu positiven Werten übergegangen wird, geht es durch Null. Tatsächlich sind die Nullpunkte um die halbe Wellenlänge voneinander getrennt. Um gute Wellenfunktionen eines Partikels in einer Box zu erhalten, müssen wir daher Wellen auswählen, deren Länge es ermöglicht, sie in der Box zu stapeln, sodass die Nullpunkte genau an den Wänden liegen.

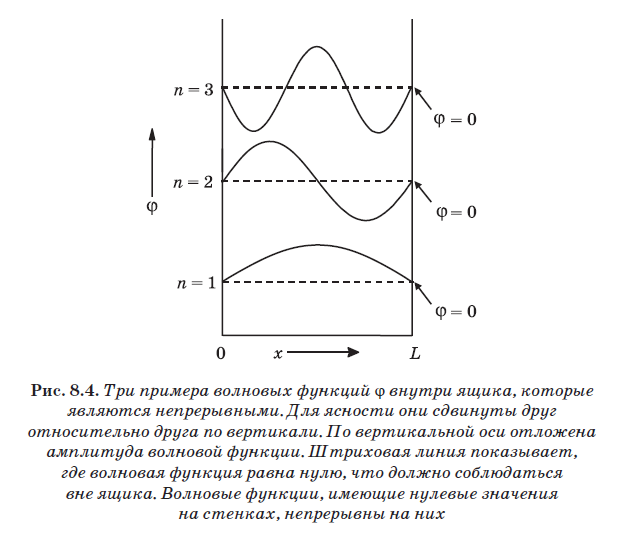
In Abb. 8.4 zeigt drei Beispiele für Wellen, die für die Rolle von Wellenfunktionen für ein Teilchen in einer Box geeignet sind. Die untere von ihnen wird mit n = 1 bezeichnet und besteht aus einer Halbwelle. Sie beginnt links bei der Amplitude 0, passiert das Maximum und fällt dann an der Wand am Punkt L wieder auf Null ab. Die nächste Welle, die sich über n = 2 befindet und aus dieser besteht, besteht aus einer vollständigen Schwingung. Es beginnt auch an der linken Wand bei der Amplitude 0, passiert einen positiven Peak, kehrt zu Null zurück, dann folgt ein negativer Peak und kehrt an Punkt L an der Wand zu Null zurück. Die durch n = 3 angegebene Welle enthält eineinhalb Perioden. Jede Welle, die eine ganzzahlige Anzahl von Halbwellen enthält, dh 1, 2, 3, 4, 5 usw., die halbe Wellenlänge und so angeordnet ist, dass sie links bei Null beginnt und rechts bei Null endet, ist geeignet.

Der Wert n ist die Anzahl der Halbwellen einer bestimmten Wellenfunktion. Für n = 1 beträgt die Wellenlänge 2L, da die Kastenlänge L ist und n = 1 der halben Wellenlänge entspricht. Für n = 2 ist die Wellenlänge L, da genau eine Wellenlänge zwischen den Wänden liegt. Für n = 3 werden drei Halbwellen zwischen die Wände gelegt, d. H. 1,5 = L. In diesem Fall = L / 1,5, d. H. = 2L / 3. Beachten Sie, dass hier eine allgemeine Regel zu finden ist: = 2L / n, wobei n eine ganze Zahl ist. Für n = 1 erhalten wir = 2L, für n = 2 - = 2L / 2, für n = 3 - = 2L / 3 usw.

»Weitere Informationen zum Buch finden Sie auf der Website des Herausgebers
» Inhalt
» Auszug

Für Leser dieses Blogs 20% Rabatt auf den Gutschein - Fire