Wie funktioniert das Higgs-Feld: 2) Warum ist das Higgs-Feld im Durchschnitt nicht Null?

Wie funktioniert das Higgs-Feld:

1. Hauptidee
2. Warum wird das Higgs-Feld ungleich Null gemittelt?
3. Wie erscheint das Higgs-Teilchen?
4. Warum ist das Higgs-Feld notwendig?

Wie kommt es, dass das Higgs-Feld in der Natur keinen Durchschnittswert von Null hat, während andere (scheinbar elementare) Naturfelder, die wir kennen, Null haben? [Sehr kleines Druckbild: Andere Felder, mit Ausnahme des Gravitationsfelds der untersten Ebene, werden als metrisch bezeichnet. Auf diese Weise können Sie die Existenz von Raum und Zeit bestimmen.]

Erstens können Fermionfelder in der Natur keinen großen konstanten Wert ungleich Null haben. Dies ist auf den Unterschied zwischen Fermionen und Bosonen zurückzuführen. Bosonen können im Durchschnitt ungleich Null sein, Fermionen jedoch nicht. Sie können also die Elektronen (und ihre Cousins ​​Myonen und Tau), Neutrinos und Quarks vergessen. Kleingedrucktes: Fermionen können sich miteinander oder mit Antifermionen paaren und zusammengesetzte Bosonen bilden, die im Durchschnitt ungleich Null sein können. Dies gilt für die oberen und unteren Quarks und ihre Antiquarks sowie für Elektronen in einem Supraleiter. Aber das ist eine lange Geschichte, und sie betrifft unsere nicht direkt.

Was ist mit den Feldern Photonen, Gluonen, W und Z? Das sind alles Bosonen. Im Prinzip könnten diese Felder über das Universum einen konstanten Durchschnittswert ungleich Null haben. Aber Experimente, nicht Theorie, sagen, dass dies nicht der Fall ist. Ein ausreichend großer Wert des elektrischen Feldes ungleich Null würde zum Auftreten verschiedener Effekte führen, die wir nicht beobachten. Das wichtigste davon wäre eine Verletzung der Rotationsinvarianz in großem Maßstab. Ein elektrisches Feld ist ein Vektor (Spin-1), der in eine bestimmte Richtung anzeigt. Wenn es also ungleich Null ist, sollte sich die Richtung, in der dieser Wert anzeigt, von allen anderen unterscheiden. (Abb. 1 unten links).


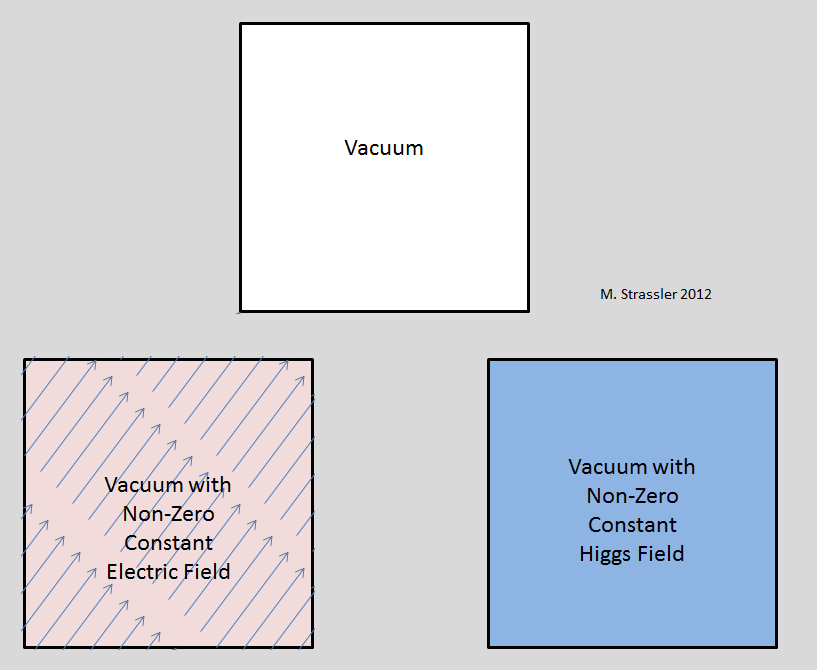Abb. 1

Das Higgs-Feld ist skalar (Spin-0) und zeigt nirgendwo etwas an. Unter anderen Skalarfeldern (weder elementar noch relativistisch) können wir Beispiele für das Luftdichtefeld, das Druckfeld innerhalb der Erde und die Meerestemperatur nennen. Zu jedem Zeitpunkt und zu jedem Zeitpunkt ist Dichte, Druck oder Temperatur nur eine Zahl, und das elektrische Feld ist eine Zahl und eine Richtung. Wenn also das Higgs-Feld einen Wert ungleich Null hat, entsteht keine Vorzugsrichtung - Abb. 1, unten rechts. Was seltsamer ist (da es relativistisch ist), erzeugt das Higgs-Feld keinen bevorzugten Referenzrahmen. Für die Luftdichte gibt es ein bevorzugtes Referenzsystem, da Sie entweder relativ zur Luft ruhen oder sich durch diese bewegen. Für das Higgs-Feld ist dies jedoch nicht der Fall. Alle Beobachter ruhen sich relativ zu ihm aus. Daher widerspricht der Erfolg von Einsteins SRT, die alle Arten von Phänomenen beschreibt, nicht dem Vorhandensein eines relativistischen Skalarfeldes mit einem Wert ungleich Null wie dem Higgs-Feld. Kurz gesagt, in Gegenwart eines Higgs-Feldes ungleich Null verhält sich das Vakuum genau so, wie es sich bei H = 0 verhalten würde; Sein Vorhandensein kann nur durch die Wirkung auf die Masse der Partikel nachgewiesen werden (oder durch etwas Dramatischeres, beispielsweise die Verwendung von LHC zur Erzeugung von Higgs-Partikeln).

Der einfachste Weg für das Higgs-Feld wäre, im gesamten Universum einen Wert ungleich Null beizubehalten, wenn ein Gleichgewichtswert H ₀ ungleich Null an seiner Bewegungsgleichung der Klasse 1 beteiligt wäre:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - (2 \ pi \ nu_ {min}) ^ 2 (H - H_0)$$

(Es sollte Klasse 1 sein, nicht Klasse 0, aus Gründen, die uns nach Erörterung des Higgs-Partikels klar werden). In der Tat ist die Situation etwas komplizierter. Die richtige Gleichung würde folgendermaßen aussehen:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = a ^ 2 H - b ^ 2 H ^ 3$$

Wobei a und b Konstanten sind (ihre Quadrate sind positiv! Beachten Sie das Pluszeichen vor a ² H und vergleichen Sie es mit dem Minus in der vorherigen Gleichung), über das wir später erfahren werden. Dies kann wie folgt umgeschrieben werden:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - [a / b] ^ 2)$$

Wenn H (x, t) eine räumliche und zeitliche Konstante ist, dann ist dH / dt = dH / dx = 0

$$

$$0 = - b2 H (H2 - [a / b] ^ 2)$$

(wenn H (x, t) eine Konstante in x und t ist) und er Lösungen hat (im Moment werden wir alles stark vereinfachen):

1. H = 0
2. H = + a / b
3. H = - a / b

Mit anderen Worten, die Gleichgewichtspositionen sind drei, nicht eins. Kleingedrucktes: Ich vereinfache es hier stark, aber unbeschadet der Bedeutung.

Dies ist nicht sofort klar, aber die Lösung H = 0 ist instabil. Die Situation ist ähnlich der Bewegungsgleichung einer Kugel in einer Schüssel der in Fig. 1 gezeigten Form. 2 - ähnlich dem Boden einer Weinflasche. Er hat auch drei Gleichgewichtspositionen, eine bei 0 und zwei bei ± x ₀ . Aber offensichtlich ist die Position bei 0 instabil - jeder Stoß führt dazu, dass der rote Ball weit von x = 0 rollt, eine grundlegende Änderung der Situation. Umgekehrt ist das Gleichgewicht bei x = x ₀ stabil, da bei jedem Druck die grüne Kugel mit einer kleinen Amplitude um den Punkt x = x ₀ schwingt - dies ist keine so drastische Änderung. Gleiches gilt für eine hellgrüne Kugel bei x = -x ₀ . Obwohl H = 0 die Lösung für die Gleichung für das Higgs-Feld sein wird, erwies sich die Geschichte unseres Universums als kompliziert genug, um zu gewährleisten, dass das Higgs-Feld richtig getreten werden sollte, sodass es nicht in dieser Position bleiben konnte. Stattdessen befand sich das Higgs-Feld in einer Lösung mit einem Wert ungleich Null und in einer stabilen Situation.



Dank einer Kombination aus Experimenten und Theorie wussten wir jahrzehntelang, dass der Wert des Higgs-Feldes (das traditionell als "v" bezeichnet wird) 246 GeV beträgt. Dies gibt uns eine Vorstellung von diesen Konstanten a und b:

a = vb = (246 GeV) b

Somit können wir a bis b bestimmen und die Higgs-Bewegungsgleichung umschreiben:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - v ^ 2)$$

Dies gibt uns jedoch keine Vorstellung von b selbst. Im nächsten Artikel werden wir mehr über ihn erfahren.

Obwohl ich alles so vorbereitet habe, dass H gleich v oder –v sein kann, spielt es keine Rolle, ob das Higgs-Feld positiv oder negativ ist (tatsächlich gibt es noch mehr Möglichkeiten, siehe unten); Die Welt wird mit der gleichen Physik genauso ausfallen, da nichts vom Zeichen von H abhängt. Es wird nicht sofort offensichtlich, aber es ist; Ein Hinweis - wo immer Sie H in den von mir beschriebenen Gleichungen oder in der Beschreibung der Funktionsweise des Higgs-Feldes finden, erscheint H ² überall und nicht nur H - und H ² hängt nicht von H = v oder H = -v ab . [Kleingedrucktes: Tatsächlich ist H ein komplexes Feld mit Real- und Imaginärteil, sodass H gleich dem v-fachen einer komplexen Zahl z sein kann, für die | z | = 1; und tatsächlich ist H * H = | H | ² , aber es kommt nicht auf z an. Und selbst das ist noch nicht alles! Aber genug für heute.]

Wenn Sie einen Weg finden (zum Beispiel durch Kollision von Protonen am Large Hadron Collider), um Störungen in das Higgs-Feld zu drücken oder einzuführen, schwingt es hin und her - das heißt, Wellen erscheinen in der Form darin

$$

$$H = v + A cos [2 \ pi (\ nu t - x / \ lambda)]$$

Wobei A die Wellenamplitude ist, sind ν und λ die Frequenz und Wellenlänge, und die Beziehung zwischen ν und λ hängt von der genauen Form der Bewegungsgleichung ab, insbesondere von b und v. Da das Higgs-Feld ein Quantenfeld ist, wird die Amplitude dieser Wellen quantisiert, und das Quantum dieser Wellen ist das, was wir das Higgs-Teilchen nennen. Das nächste Mal werden wir die Eigenschaften dieser Partikel betrachten.