Hallo, ich heiße Alexander und bin Physiker. Von außen mag dies wie ein Urteil klingen, ist es aber tatsächlich. Es stellte sich heraus, dass ich Grundlagenforschung in der Physik betreibe, nämlich beschleunigte geladene Teilchen: Protonen und all diese größeren sind positive Ionen, das heißt. In Studien verwende ich keine großen Beschleuniger wie LHCs, aber ich schieße mit einem Laser auf die Folie, und ein Protonenimpuls fliegt aus der Folie.



Nun ein paar Worte zu mir. Ich absolvierte die Fakultät für Photonik und Optoinformatik des ITMO in St. Petersburg, ging dann zu einer Magistratur an der Aalto-Universität (dies ist in Finnland) in Richtung Mikro- und Nanotechnologie und spuckte dann auf all diese kleinen Dinge, Mikroskope und insbesondere auf einen Reinraum. Und ich bin mit großen Lasern in die Grundlagenforschung gegangen. Jetzt arbeite ich in einer Graduiertenschule im Südwesten Schwedens in der Stadt Lund an der gleichnamigen Universität. Dies ist ungefähr die Entfernung einer Kanone von Kopenhagen.

Wie beschleunigt, so flog

Beschleuniger geladener Teilchen selbst sind keine neue Idee, aber die Methode, mit der ich sie beschleunige, ist relativ frisch, ungefähr so ​​alt wie ich. Dadurch können Sie die Größe des Beschleunigers und seine Kosten, einschließlich der Kosten für Arbeit und Wartung, erheblich reduzieren. Der Unterschied zwischen den beiden Typen kann im Bild unten geschätzt werden.

Links ist ein elektrostatischer Linearbeschleuniger (leicht zerlegt); Rechts ist mein kleiner, aber stolzer Folienlochmacher

Vergleichen wir diese beiden Muster des düsteren physischen Genies genauer. Schauen Sie sich das linke und das rechte Gaspedal an, dann wieder links und wieder rechts: Ja, meins ist auf einem Pferd (ein Witz - Kommentar des Autors). Tatsächlich hat meine nur einen Meter Durchmesser und die Protonen selbst werden von einem Stück Folie beschleunigt. Sein Halter befindet sich genau in der Mitte des Kreises und trägt einen schönen Kupferrock. Es ist viel einfacher und kompakter als die linke Probe, die die Größe eines Busses hat und zusätzlich mit erstickendem Gas gefüllt ist. Wenn man sich also in Hülle und Fülle behauptet hat (in der Physik kommt es häufig vor, dass je kleiner desto besser), kann man sich der Physik des Beschleunigungsprozesses zuwenden.

Da wir geladene Teilchen beschleunigen, ist es am logischsten, dies mit einem elektrischen Feld zu tun. Das Feld werden wir durch Spannung charakterisieren. Für diejenigen, die nach der Schule zum vorderen und hinteren Ende gegangen sind, möchte ich Sie daran erinnern: Die elektrische Feldstärke ist eine vektorphysikalische Größe, die das elektrische Feld an einem bestimmten Punkt charakterisiert und numerisch gleich dem Verhältnis der Kraft ist, die auf eine an einem bestimmten Punkt im Feld platzierte Festpunktladung wirkt. die Höhe dieser Ladung (Dirty Copy-Paste aus Wikipedia). Es hat eine Abmessung von V / m. Zurück zum Vergleich: Der Beschleuniger links beschleunigt die Protonen auf 4 MeV (Megaelektronvolt), dh 2,77 * 10 ⁷ m / s oder 9,2% der Lichtgeschwindigkeit. Da die Protonenladung 1 beträgt und die Länge des Beschleunigers zwei Meter beträgt, beträgt die Feldstärke 2 MV / m. Hier haben wir angenommen, dass das Feld an allen Orten in eine Richtung gerichtet ist und im Allgemeinen der Wahrheit sehr nahe kommt. Ein stilvoller Beschleuniger hat eine Feldstärke in der Größenordnung von mehreren Fernsehern / m, dh etwa eine Million Mal mehr. Dennoch ist es erwähnenswert, dass seine Länge nur wenige Mikrometer beträgt.

An diesem Punkt haben wir also herausgefunden, wessen Feld steiler ist. Es ist Zeit, sich den physikalischen und technischen Mechanismen zuzuwenden, die dieses Feld schafft. Bei einem herkömmlichen Beschleuniger gibt es zwei Bleche, von denen eines negativ geladen ist und das zweite in keiner Weise. Erinnern Sie sich an das Schulexperiment über das Reiben eines Ebonitsticks mit einem Stück Wolle. Hier ist das Prinzip genau das gleiche, aber die Ausführung ist viel komplizierter. Wenn Sie Protonen von der Folie beschleunigen, wird das Feld von Elektronen erzeugt, Elektronen fliegen aus dem heißen Plasma heraus, das Plasma wird von einem Laser erhalten und erwärmt, und all dies ist der Rest des Pfostens.

Soll ich ihn schlagen und er verwandelt sich in einen Fleck?

Wenn Sie hart genug schlagen, können Sie viele wunderbare physikalische Phänomene sehen. So haben die Harvard-Leute metallischen Wasserstoff bekommen und ihn dann verloren.

In meinem Fall schieße ich die Folie mit einem Laser. Ich werde es genauer beschreiben, nachdem ich die nicht triviale Physik der Prozesse zur Gewinnung von warmer dichter Materie erklärt habe. Dies ist in wissenschaftlichen Begriffen genau der Name des Plasmas, das für den Triumph der Beschleunigung meiner Protonen verantwortlich ist. Und jetzt das Wichtigste zuerst.

Der Laser erzeugt Impulse mit einer Wellenlänge von 800 nm und 35 fs für eine Dauer ( ^10-15 s), ^dh die tatsächliche Impulslänge im Vakuum beträgt ca. 10 µm. Ungefähr 2 J Energie werden in diesen Impuls gesteckt, und das ist viel. Wenn wir diesen Impuls nehmen und ihn auf eine Folie zu einem sauberen runden Fleck mit einem Durchmesser von 5 Mikrometern fokussieren, liegt die Intensität in der Größenordnung von 10 ²⁰ W / cm ² . Das ist sehr unanständig. Nochmals ein paar Vergleiche: Stahl kann leicht mit einer Intensität von 10 ⁸ W / cm ² (oder so) geschnitten werden.

Aufgrund der Konstruktionsmerkmale des Verstärkers hat der Laserpuls einen vorhergehenden Sockel mit einer Dauer von ungefähr 500 ps, ​​und dieser Sockel trägt wesentlich dazu bei, Protonen gut zu beschleunigen.

Ionisiert - bedeutet bewaffnet

Erinnern Sie sich daran, was mit Licht passiert, wenn es in eine Substanz eindringt. Energie muss erhalten bleiben, dh es gibt nur drei Varianten von Ereignissen: Reflexion, Transmission und Absorption. In einem harten Leben sind alle oben genannten Dinge gleichzeitig vorhanden. Schon sehr früh sind wir an Absorption interessiert.

Wir haben also einen Sockel, auf den wir uns auch perfekt konzentrieren, und der dort perfekt absorbiert wird. Um nicht auf die Komplexität der Festkörperphysik einzugehen, betrachten wir die Absorption eines eigenständigen Atoms. Aus der Quantenmechanik wissen wir, dass nur ein Photon absorbiert werden kann, dessen Energie genau der Energie des Übergangs eines Elektrons von einem Zustand in einen anderen entspricht. Wenn die Photonenenergie größer ist als die Ionisierungsenergie (dh ein Elektron aus dem Nest der Eltern zu einer freien Reise schicken), geht der Überschuss in die kinetische Energie des Elektrons, alles ist einfach. In unserem Fall haben Photonen mit einer Wellenlänge von 800 nm nicht genug Energie (dies ist die Energie eines Photons, nicht des gesamten Pulses!), Um das Ziel zu ionisieren, aber hier hilft uns die Physik. Erinnerst du dich, ich habe eine größere Strahlungsintensität erwähnt? Wenn wir uns im Anhang noch daran erinnern, dass Licht als Photonenfluss dargestellt werden kann und die Intensität direkt proportional dazu ist, stellt sich heraus, dass der Photonenfluss sehr groß ist. Und wenn der Fluss so groß ist, ist es wahrscheinlich, dass mehrere Photonen am selben Ort und zur selben Zeit ankommen, und wenn ihre Energie absorbiert wird, addieren sie sich und es kommt immer noch zu einer Ionisierung. Seltsamerweise wird dieses Phänomen als Multiphotonenionisation bezeichnet und wir verwenden es regelmäßig.

Im Moment haben wir, dass die Elektronen erfolgreich abgerissen wurden, was bedeutet, dass der Hauptimpuls am fertigen Plasma ankommt und es zu erwärmen beginnt.

Grundlagen der Plasmaphysik (hat sich keinen Witz ausgedacht, ah)

Vor dem Erhitzen lohnt es sich, ein wenig über Plasma als Materiezustand zu sprechen. Plasma, es ist wie ein Gas, nur Elektronen sind getrennt und Kerne sind getrennt. Wir werden unser Plasma als ein nahezu ideales Gas betrachten, das jedoch aus Elektronen besteht.

Unser Hauptmerkmal eines Plasmas ist seine Dichte (die Anzahl der Elektronen pro Volumeneinheit), dieser Wert wird mit $ n_e $ bezeichnet (nicht zu verwechseln mit dem Brechungsindex!) Und die Temperatur dieser Elektronen, d. H. Ihre Durchschnittsgeschwindigkeit. Dies wird durch die Boltzmann-Verteilung wie im Schulphysikkurs beschrieben:

$$$$ display $$ \ frac {m_e v ^ 2} {2} = \ frac {1} {2} k_B T_e, $$ display $$

wo leicht folgt

$$$$ display $$ \ langle v \ rangle = \ sqrt [] {k_B T_e / m_e}, $$ display $$

wo$$ $ inline $ k_B $ inline $ - Boltzmann-Konstante$$ $ inline $ T_e $ inline $ Ist die Elektronentemperatur und$$ $ inline $ m_e $ inline $ Ist die Masse des Elektrons. Ja, hier haben wir einen eindimensionalen Fall betrachtet, aber wir brauchen wirklich nicht mehr, um unsere Prozesse zu beschreiben.

Nun legen wir ein elektrisches Feld an das bereits beschriebene Plasma an. Ich möchte Sie daran erinnern, dass Plasma aus geladenen Teilchen besteht, was bedeutet, dass bei einer bestimmten Dichte in einem bestimmten Abstand von der Stelle, an der wir das Feld angelegt haben, die Elektronen die Quelle verdecken (abschirmen) (eine solche Menge kleiner Matrosovs - Anmerkung des Autors). Der dafür notwendige Abstand wird als Debye-Länge bezeichnet und ist durch die Gleichung gegeben

$$$$ display $$ \ lambda_D = \ sqrt [] {\ frac {\ epsilon_0 k_B T_e} {q ^ 2_e n_e}}. $$ Anzeige $$

Hier$$ $ inline $ q_e $ inline $ offensichtlich die Ladung eines Elektrons, und$$ $ inline $ \ epsilon_0 $ inline $ - Dielektrizitätskonstante des Vakuums, eine solche Grundkonstante. Wir analysieren diese Formel ein wenig, um die einfache Physik des Prozesses zu sehen. Wenn wir die Dichte der Elektronen erhöhen, verringern wir den durchschnittlichen Abstand zwischen ihnen. Infolgedessen sammeln wir für einen kleineren Abstand genügend Elektronen, um unser Feld vollständig abzuschirmen. Andererseits ist der durchschnittliche Abstand zwischen den Elektronen umso größer, je höher die Temperatur ist.

Aufgrund des Screening-Effekts und einer genau definierten Durchschnittstemperatur der Elektronen (abhängig von der Temperatur) reagiert das Plasma nicht sofort auf ein plötzlich eintreffendes Feld. Es ist logisch anzunehmen, dass die Reaktionszeit mit der Debye-Länge und der Elektronengeschwindigkeit zusammenhängt. Eine gute Analogie ist es, einen Stein auf einen See zu werfen. Im Vergleich zu einem ganzen See wirkt der Stein punktuell auf die Wasseroberfläche. Ein Teil des Wassers ändert sich sofort (hier floppte es), und dann beginnen sich die Wellen über die Wasseroberfläche auszubreiten. Im Falle von Plasma ist ein plötzlich auftretendes elektrisches Feld ein Stein. Die Größe der Wolke wird durch die Länge des Bildschirms bestimmt (das Feld wirkt nicht darüber hinaus), und die Ausbreitung der Wellen hängt davon ab, wie nahe die Elektronen beieinander liegen. Wir können eine solche Eigenschaft wie die Plasma-Reaktionszeit einführen:

$$$ inline $ t_D = \ lambda_D / v $ inline $ . Im Großen und Ganzen zeigt es uns die Zeit, in der Informationen über eine Änderung des angelegten Feldes jene Elektronen erreichen, die sie sozusagen nicht gesehen haben.

Da wir Physiker sind, mögen wir Zeit nicht wirklich. Es ist viel bequemer, mit Frequenzen zu arbeiten, daher führen wir das Konzept der Eigenfrequenz eines Plasmas ein. Dieser Wert zeigt uns, wie oft wir das Feld ändern können, damit die gesamte Elektronenakkumulation, die wir stolz Plasma nennen, Zeit hat, auf diese Änderungen zu reagieren. Was könnte einfacher sein? Teilen Sie die Einheit durch die Reaktionszeit, und hier ist es - die Frequenz:

$$$$ display $$ \ omega_p = \ frac {1} {t_D} = \ sqrt [] {\ frac {q ^ 2_e n_e} {\ epsilon_0 m_e}}. $$ Anzeige $$

Es ist leicht zu erkennen, dass die Eigenfrequenz der Plasmaoszillationen von der Elektronendichte abhängt. Je mehr Elektronen, desto höher die Frequenz. Sie können eine andere Analogie ziehen, diesmal jedoch mit einem Federpendel. Die hohe Elektronendichte zeigt, dass sie näher beieinander liegen, was bedeutet, dass sie stärker interagieren. Wir nehmen an, dass ihre Wechselwirkung in direktem Verhältnis mit der Federelastizität des Pendels zusammenhängt. Und je größer die Elastizität ist, desto höher ist die Schwingungsfrequenz.

Die Eigenfrequenz eines Plasmas bestimmt auch seinen Brechungsindex. Um ehrlich zu sein, schreiben wir die Wellengleichung der kollektiven Bewegung von Elektronen in einem Plasma und nehmen dann kleine Änderungen der Elektronendichte an (wir werden dies hier nicht tun, weil es langweilig ist), dann setzen wir den Brechungsindex wie folgt:

$$$$ display $$ \ eta = \ sqrt [] {1- \ frac {\ omega ^ 2_p} {\ omega ^ 2_0}}. $$ Anzeige $$

Hier$$ $ inline $ \ omega_0 $ inline $ Ist die Kreisfrequenz des angelegten elektrischen Feldes. Sie ist in rad / s und nicht in Hz!

Wir schauen uns diesen Ausdruck genau an. Als experimenteller Physiker trinke ich keine Seelen in reellen Zahlen, aber ich versuche, komplexe zu ignorieren, insbesondere den komplexen Brechungsindex. Nun, wie kann sich Licht am Ende in Materie i- mal langsamer ausbreiten als im Vakuum? Das ist eine Art Unsinn! Nicht wirklich, aber dazu ein anderes Mal mehr. Wenn$$ $ inline $ \ omega_0> \ omega_p $ inline $ Dann hat der Ausdruck eine echte Bedeutung und ein elektrisches Wechselfeld breitet sich in unserem Plasma aus. Jeder ist glücklich, und wir werden ein solches Plasma als unzureichend dicht bezeichnen. Wenn jedoch$$ $ inline $ \ omega_0 <\ omega_p $ inline $ dann wird der Brechungsindex nicht nur komplex, sondern völlig imaginär. In diesem Fall (und nicht nur, weil ich es wollte) breitet sich die Welle dort überhaupt nicht aus, sondern wird sofort ohne Verlust reflektiert. Dies ist zu dichtes Plasma. Ein sehr cooles Phänomen übrigens. Es wird ein Plasmaspiegel genannt.

Und als Nachtisch$$ $ inline $ \ omega_0 = \ omega_p $ inline $ . Dies ist ein Plasma mit kritischer Dichte. In diesem Fall beginnt es mit einem (von uns gelieferten) elektrischen Wechselfeld in Resonanz zu treten. Für einen solchen Sonderfall können Sie sogar das Konzept der kritischen Dichte einführen und folgendermaßen definieren:

$$$$ display $$ n_c = \ frac {\ epsilon_0 m_e \ omega ^ 2_0} {q ^ 2_e}. $$ Anzeige $$

Natürlich ist die kritische Dichte für jede Frequenz des Forcierungsfeldes unterschiedlich.

SCHOCK! Plasmaheizung! Dazu nur ...

In unserem Fall konzentrieren wir uns nur auf einen Heizmechanismus, der im Experiment vorherrscht.

Lassen Sie das Plasma, das wir vom Sockel gebildet haben, zunächst einen glatten Dichtegradienten haben. In diesem Fall erwärmen wir uns durch Resonanzabsorption. Eine Illustration davon im Bild unten.


Darstellung des Resonanzabsorptionsprozesses: a) Elektronendichteverteilung nahe der Vorderseite des Targets; b) Brechung eines Laserstrahls in einem Plasma mit einem Dichtegradienten; c) das elektrische Feld im Plasma

Der Laser scheint also in einem Winkel auf unser Plasma, also sei es 45 Grad, und gleichzeitig ist er in der Einfallsebene polarisiert. Die Polarisation ist in der Abbildung durch rote Pfeile gekennzeichnet. Unser Plasma hat einen Dichtegradienten, was bedeutet, dass sich sein Brechungsindex ständig ändert (hier wächst er). Irgendwann wird es vorkommen, dass eine bestimmte Plasmaschicht für unseren Laser „rotierend“ wird und reflektiert, dh sich für einige Zeit parallel zur kritischen Schicht ausbreitet. Es ist wichtig zu beachten, dass es sich dreht, bevor es die Schicht mit der kritischen Dichte erreicht, da wir es in einem Winkel zur Normalen gestartet haben. Die Plasmadichte, mit der sich der Laserstrahl dreht, ergibt sich aus dieser Gleichung:

$$$$ Anzeige $$ n_t = n_c \ cos ^ 2 \ alpha, $$ Anzeige $$

wo$$ $ inline $ n_c $ inline $ Ist die kritische Dichte und$$ $ inline $ \ alpha $ inline $ - Einfallswinkel des Lichts.

Jetzt beginnt der Spaß. Denken Sie daran, dass Licht nicht nur ein Photonenfluss ist, sondern auch eine elektromagnetische Welle, dh unser Impuls hat ein elektrisches Feld, das harmonisch mit einer großen Amplitude schwingt. Wenn sich Licht parallel zur kritischen Schicht ausbreitet, bildet sich eine stehende Welle, die sich im Laufe der Zeit nicht ändert (natürlich solange der Laserpuls vorhanden ist). Das Feld dieser Welle dringt tatsächlich weiter als die Plasmaschicht ein, in der sich das Licht gedreht hat, und erreicht die kritische Schicht. Ich möchte Sie daran erinnern, dass die Frequenz der Plasmaoszillationen in der kritischen Schicht der Frequenz der Laserstrahlung entspricht, was bedeutet, dass Resonanz auftritt. Wenn der Laser aufhört zu leuchten, wird die Energie, die er an die Elektronen in der kritischen Schicht überträgt, durch Stöße auf die anderen Elektronen verteilt, was bedeutet, dass das Plasma erwärmt wird.

Wo ist eigentlich die Beschleunigung?

Nachdem wir die Elektronen im Plasma gut erwärmt haben und der Laser nicht mehr leuchtet, können wir feststellen, wie Protonen beschleunigt werden. Schauen Sie sich dazu die Bilder unten an. Bis zu diesem Punkt habe ich nie gesagt, woher die Protonen kommen. Natürlich erscheinen sie nicht aus den Kernen des Folienmaterials. Da wir nicht sehr ordentlich sind und keine Handschuhe tragen (Hände schwitzen stark darin), befinden sich Wasser und Kohlenwasserstoffe auf der Oberfläche der Folie. Ionisierter Wasserstoff ist unsere unschätzbare Protonenquelle. Aktiviert: Wenn Sie die Verschmutzung entfernen, gibt es keine Protonen.

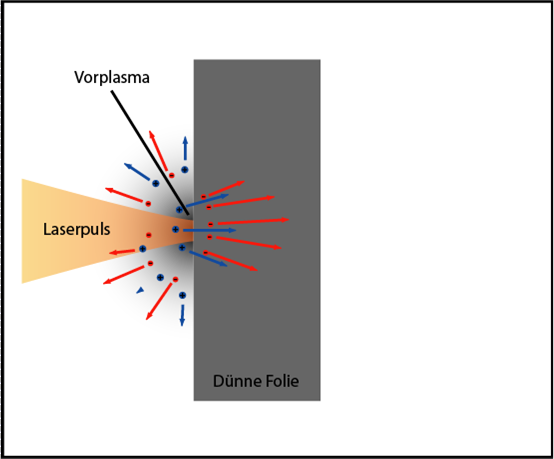	Die Bildung von Plasma durch einen Sockel, d. H. Ionisation der Vorderseite des Ziels. Als Ziel wird üblicherweise eine Folie mit einer Dicke von 0,4 bis 12 Mikrometern verwendet.
	Hier interagiert der Hauptteil des Pulses mit dem erzeugten Plasma und erwärmt es. Einige Elektronen haben sich so gut erwärmt, dass sie von der Rückseite des Ziels herausfliegen.
	Wenn ziemlich viele Elektronen herausfliegen, zieht die verbleibende positive Ladung in der Folie sie zurück. Im Plasma erwärmen sie sich wieder und fliegen heraus. Für eine Weile stellt sich ein dynamisches Gleichgewicht ein. Das elektrische Feld ist senkrecht zum Ziel gerichtet
	Dieses sehr elektrische Feld löst Protonen und andere Ionen (je nachdem, was überhaupt vorhanden war) von der Rückseite des Ziels und beschleunigt sie dann. Wenn sich die Ionen beschleunigt haben, fällt die Elektronenwolke bereits auseinander und alle Teilchen beginnen weiter zusammen zu fliegen. Und dann beginnen wir zu glauben, dass sie nicht mehr interagieren.

Teilen und erobern

Im Moment ist die Position folgende: Der Laser hat lange nicht mehr geleuchtet, es gibt ein Loch in der Folie, Protonen mit Elektronen fliegen freundlich vom Ziel normal zu seiner Rückseite. Wir brauchen überhaupt keine Elektronen, deshalb hilft uns ein Magnet. Wenn ein Strahl geladener Teilchen durch ein Magnetfeld fliegt, werden die Lorentzkräfte jedes Teilchens proportional zu seiner Geschwindigkeit und Ladung abgelenkt. Dementsprechend werden Protonen und Elektronen in verschiedene Richtungen abweichen, und wir werden einfach nicht in die Richtung von Elektronen schauen. Übrigens, je größer die Energie des Protons (dh seine Geschwindigkeit) ist, desto weniger wird es abweichen. Dies bedeutet, dass wir durch Platzieren eines für Protonen empfindlichen Bildschirms die Energien beschleunigter Protonen sehen können. Noch ein paar Vergleiche in Zahlen: ein Magnet, der permanent bei uns steht und ein Feld von ca. 0,75 T erzeugt; In MRT-Geräten beträgt das Magnetfeld 1,5 - 3 T.

Außerdem können wir das Profil eines Strahls fliegender Protonen sehen. Es ist übrigens rund. Und wenn wir auch die Protonenenergie in jedem Teil des Strahls messen können, können wir die Form der Elektronenwolke, die unsere Protonen beschleunigte, auf einzigartige Weise wiederherstellen.

Anstelle einer Schlussfolgerung

Es kann sich eine faire Frage stellen, warum dies alles notwendig ist. Meine Lieblingsantwort ist einfach so.Dies ist eine grundlegende Wissenschaft, und es ist sinnlos, zu versuchen, ihre momentanen Anwendungen zu finden. Vielleicht wird es in einigen Jahren seine Anwendung in der Behandlung von Krebs oder der Kernfusion finden, aber im Moment besteht die Hauptaufgabe darin, einfach so etwas Neues über die Welt um uns herum zu lernen, weil es interessant ist.

Für diejenigen, die besonders neugierig auf den Laser selbst und sein Gerät sind

Wie versprochen werde ich hier über den Laser sprechen, mit dessen Hilfe ich Wissenschaft mache. Ich habe bereits einige Eigenschaften unseres Lasers erwähnt, aber nicht über die Pulswiederholungsrate gesprochen. Es ist ungefähr 80 MHz. Diese Frequenz wird nur durch die Länge des Resonators und die Umkehrung der Zeit bestimmt, in der das Licht über den Resonator hin und her fliegen kann. Mit Blick auf die Zukunft werde ich sagen, dass es unpraktisch ist, Impulse mit einer solchen Frequenz zu verstärken, aus technischer Sicht unglaublich schwierig ist und Sie keinen Strom sparen können.

Ich werde nicht besonders auf die Lasertheorie eingehen. Die Grundlagen, woher Laserstrahlung kommt, sind in einem Wikipedia-Artikel über stimulierte Emission perfekt beschrieben. Wenn Sie versuchen, sehr kurz zu sein, werden drei Komponenten für die Laserstrahlung benötigt: das aktive Medium (Photonen fliegen ebenfalls heraus), das Pumpen (es hält das aktive Medium in einem Zustand, in dem mehr angeregte Atome emittieren können) und auch ein Resonator ( es stellt sicher, dass sich Photonen während mehrerer Durchgänge durch das aktive Medium gegenseitig kopieren). Wenn Sie alle Komponenten zusammenfügen und beten, beginnt der Laser zu leuchten, aber kontinuierlich. Wenn Sie es erneut versuchen, können Sie ihn Impulse erzeugen lassen, einschließlich solcher, die so kurz sind wie bei meiner Installation. Für die Neugierigsten,Das Verfahren zum Erzeugen von Femtosekundenimpulsen wird als passive Modenkopplung bezeichnet. Und jetzt ein kleines Merkmal von gut, sehr kurzen Impulsen. Es wird oft angenommen, dass der Laser bei derselben Wellenlänge leuchtet, und im kontinuierlichen Modus sowie bei langen Impulsen kann dies sogar als wahr bezeichnet werden. Aufgrund einer Reihe komplexer physikalischer Prozesse, auf die wir hier sicherlich nicht eingehen werden, hängen die zeitliche Form des Impulses und sein Spektrum durch die Fourier-Transformation zusammen. Das heißt, je kürzer der Puls ist, desto breiter ist sein Spektrum.Die zeitliche Form des Impulses und sein Spektrum werden durch die Fourier-Transformation in Beziehung gesetzt. Das heißt, je kürzer der Puls ist, desto breiter ist sein Spektrum.Die zeitliche Form des Impulses und sein Spektrum werden durch die Fourier-Transformation in Beziehung gesetzt. Das heißt, je kürzer der Puls ist, desto breiter ist sein Spektrum.

Angenommen, wir haben einen Master-Oszillator gestartet, aber die Energie seiner Impulse beträgt mehrere nJ. Denken Sie daran, am Anfang habe ich gesagt, dass die Energie in einem Impuls, der an einem Ziel ankommt, ungefähr 2 J beträgt? Das ist also eine Milliarde Mal mehr. Dies bedeutet, dass die Dynamik verstärkt werden muss, und wir werden ausführlicher darüber sprechen.

Kurze Impulse sind im Allgemeinen durch sehr große Spitzenleistungen gekennzeichnet (erinnern Sie sich, teilen Sie die Energie nach Zeit?), Und dies hat eine Reihe von Komplikationen. Wenn das Medium mit Strahlung hoher Intensität (Leistung pro Flächeneinheit) beleuchtet wird, brennt es, und wenn das aktive Medium verbrannt wird, wird nichts verstärkt. Deshalb wählen wir eine Wiederholungsrate von 10 Hz und verstärken nur diese. Da es viele Geräte gibt und alle mit einer solchen Frequenz arbeiten, haben wir eine spezielle Box, die diese 10 Hz auf das gesamte Bügeleisen verteilt. Für jedes Gerät können Sie die Verzögerung beim Empfang des Signals mit einer Genauigkeit von einigen Pikosekunden auswählen.

Es gibt zwei Möglichkeiten, mit hoher Intensität umzugehen. Wie Sie anhand der Definition leicht erraten können, müssen Sie entweder die Fläche vergrößern oder die Leistung verringern. Mit der ersten ist alles sehr klar, aber die zweite Methode war ein Durchbruch in der Lasertechnologie im 20. Jahrhundert. Wenn der Impuls anfangs sehr kurz ist, kann er gedehnt, verstärkt und dann wieder zusammengedrückt werden.

Um zu verstehen, wie das geht, wenden wir uns den Grundlagen der Optik zu. Für verschiedene Wellenlängen sind die Brechungsindizes im Medium unterschiedlich, was bedeutet (übrigens durch die Definition des Brechungsindex), dass mit zunehmendem Brechungsindex die Geschwindigkeit der Lichtausbreitung im Medium abnimmt. Und so haben wir am Mittwoch unseren Impuls gestartet, und sein roter Teil ging schneller durch das Material als der blaue, dh der Impuls wurde länger und seine Spitzenleistung sank. Hurra, jetzt brennt nichts mehr! Für tiefere Kenntnisse in diesem Bereich empfehle ich, über die Verstärkung von gechirpten Impulsen (auch bekannt als Chirped Pulse Amplification oder CPA) zu googeln und zu lesen.

Wir müssen nur noch den Impuls erhöhen, komprimieren, fokussieren und senden, um ein Loch in die Folie zu bohren!

Und jetzt ein paar Bilder mit Bildunterschriften.


. — , . , . — , . ,


. , , -.


, , . , , , . , . , , . , .


-. .


. , . ( 1000 ) . , .


, . — — . , : . . . ( ) , , , . - .


, 15 . , — . , -190 .


, . , 0,1\%. - , 160 . 960 , , . 10 . 80 , 8 .

Vielen Dank für Ihre Aufmerksamkeit!