👩🏿‍🏭 🕝 👨🏾‍🤝‍👨🏼 Wie funktioniert das Higgs-Feld: 3) Wie erscheint das Higgs-Teilchen? 🏂🏼 🧕 👒

Wie funktioniert das Higgs-Feld:

In einem früheren Artikel habe ich beschrieben, wie und warum das Higgs-Feld keinen Mittelwert von Null hat. Jetzt möchte ich beschreiben, was ein Higgs-Teilchen ist und wie seine Masse aus den Gleichungen entsteht.

Ich möchte Sie daran erinnern, dass ich, wenn das Gegenteil nicht erwähnt wird, immer die einfachste Form des Feldes und des Higgs-Teilchens beschreibe - das sogenannte Higgs Standardmodell. Komplexere Formen sind ebenfalls möglich; Beispielsweise können mehrere Higgs-Felder gleichzeitig anstelle eines existieren. Vielleicht werde ich einen komplexeren Fall in einem der folgenden Artikel beschreiben.

Bild

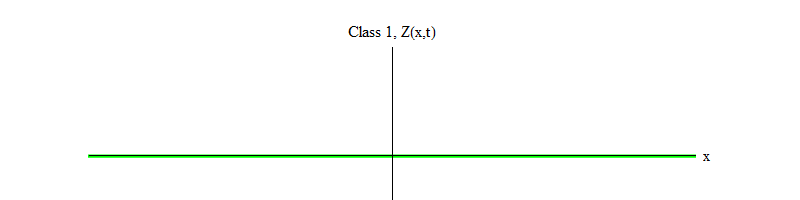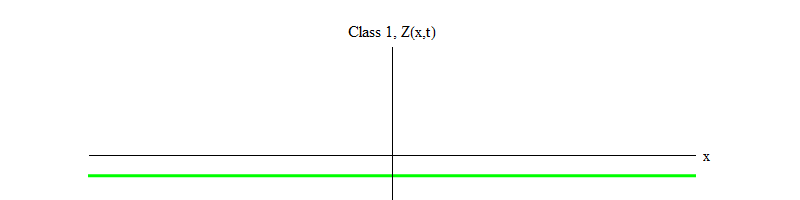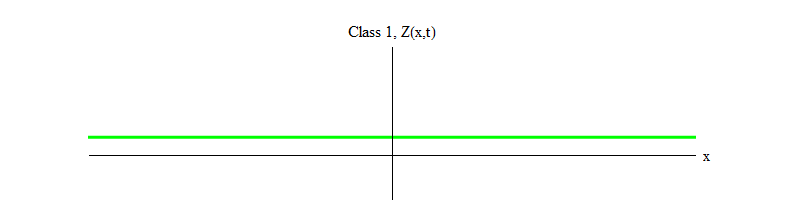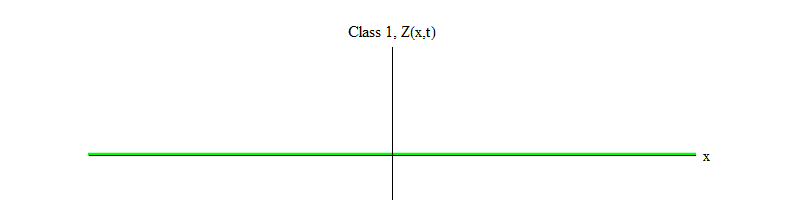Abb. 1: Ein Feld der Klasse 1 schwankt zeitlich um einen stabilen Wert Z (x, t) = 0

Im letzten Artikel habe ich diese Tatsache nicht betont, aber unter den Elementarfeldern, die wir in der Natur entdeckt haben, ist das Higgs-Feld einzigartig. Alle Felder außer Higgs erfüllen die Bewegungsgleichungen der Klasse 0 oder 1. Tatsächlich (obwohl dies wahrscheinlich nicht für alle Felder in der Natur der Fall ist) tun dies alle uns bekannten Felder, die die Gleichungen der Klasse 1 erfüllen, weil das Higgs-Feld ungleich Null ist . Wenn es Null wäre, würden sie alle Gleichungen der Klasse 0 erfüllen (wie ich im ersten Artikel erklärt habe). Stattdessen erfüllt das Higgs-Feld eine Gleichung, die als Gleichung der Klasse -1 bezeichnet werden kann.

Für das Feld Z (x, t) sehen die von mir definierten Klassen folgendermaßen aus:

d^{2} Z / d t^{2} - c^{2} d^{2} Z / d x^{2} = - B^{2} Z q u a d [K l a s s e 1 - m a s s i v T e i l c h e n] d^{2} Z / d t^{2} - c^{2} d^{2} Z / d x^{2} = 0 q u a d [K l a s s e 0 - m a s s e l o s T e i l c h e n] d^{2} Z / d t^{2} - c^{2} d^{2} Z / d x^{2} = + B^{2} Z q u a d [K l a s s e - 1 - i n s t a b i l]

$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - B ^ 2 Z \ quad [Klasse 1 - massiv \; Teilchen] \\ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0 \ quad [Klasse 0 - masselos \; Teilchen] \\ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = + B ^ 2 Z \ quad [Klasse -1 - instabil]$

Die Gleichungen implizieren, dass B ² > 0 ist.

Bild

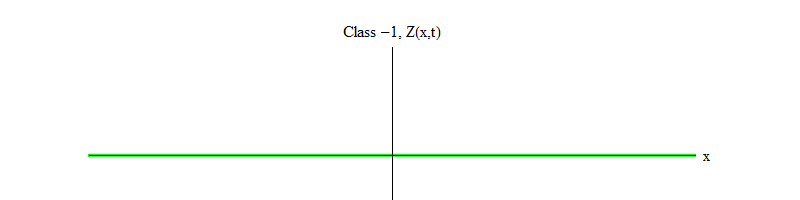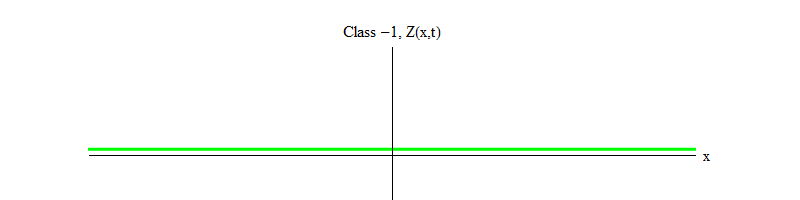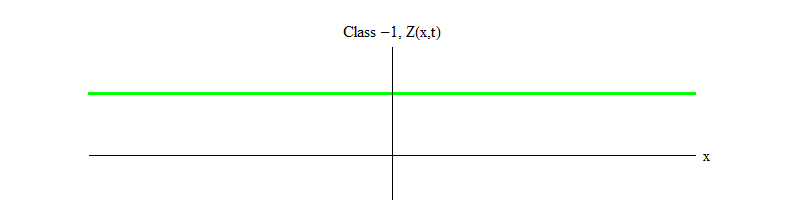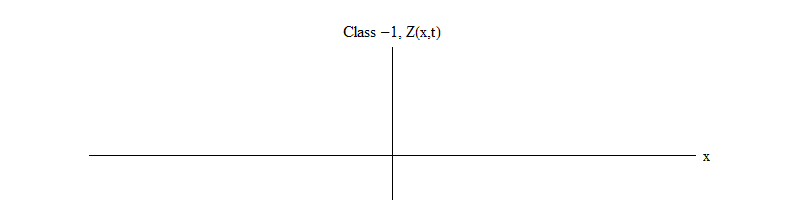Abb. 2: Ein Feld der Klasse -1 verlässt das instabile Gleichgewicht Z (x, t) = 0.

Das Minuszeichen zwischen Klasse 1 und Klasse -1 ist sehr wichtig. In beiden Fällen enthalten Lösungen der Gleichungen Z (x, t) = 0 als einen der Sonderfälle, aber für Klasse 1 ist Z (x, t) = 0 stabil, dh Z (x, t) kann um Null schwanken; Dies sind anständig verhaltene Wellen mit einem massiven Quantum. Und umgekehrt ist die Klasse -1 Z (x, t) = 0 instabil, dh Z (x, t) schwankt nicht, sondern wächst auf immer mehr Werte. Wenn Sie die Gleichung nicht ändern, fliegt die Größe des Feldes ins Unendliche. Genauer gesagt, wenn die Lösung der Gleichung der Klasse 1 die Schwingung Z ist, wie in Fig. In 1 ist die Lösung einer Gleichung der Klasse -1 ein exponentielles Wachstum von Z, wie in Fig. 1. 2.

Für das Higgs-Feld sowie für jedes in der Natur vorhandene Feld wird die Gleichung der Klasse -1 unter Verwendung von Begriffen geändert, die das exponentielle Wachstum begrenzen und verhindern, dass das Feld ins Unendliche geht. Wie wir im vorherigen Artikel gesehen haben, folgt das Higgs-Feld der Bewegungsgleichung

d^{2} H / d t^{2} - c^{2} d^{2} H / d x^{2} = - b^{2} H (H^{2} - v^{2}) = + (b v)^{2} H - b^{2} H^{3}

$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - v ^ 2) = + (bv) ^ 2 H - b ^ 2 H ^ 3$

Es gehört zur Klasse -1, wenn H fast Null ist, aber es hat ein wichtiges Mitglied von H ³ . Hier ist b eine positive Zahl und v ist die Gleichgewichtsposition für H. Diese Gleichung stellt sicher, dass das Feld H, wenn es am Punkt H = 0 beginnt und sich von der Position des instabilen Gleichgewichts zum positiven H bewegt, um die Position des stabilen Gleichgewichts in H = v schwingt (Abb. 3).

Bild

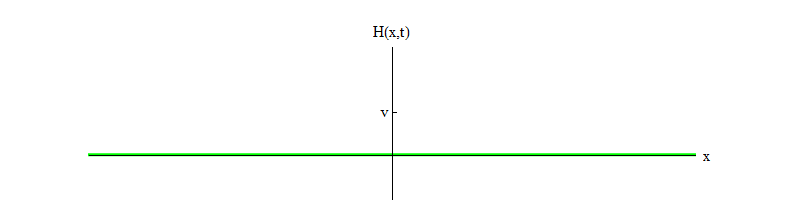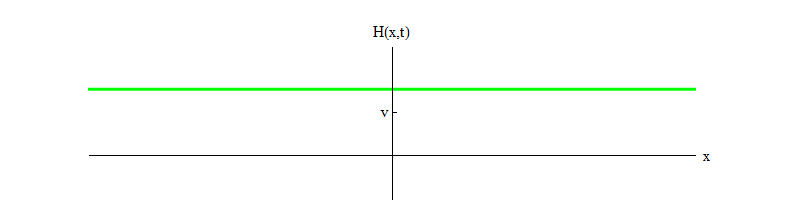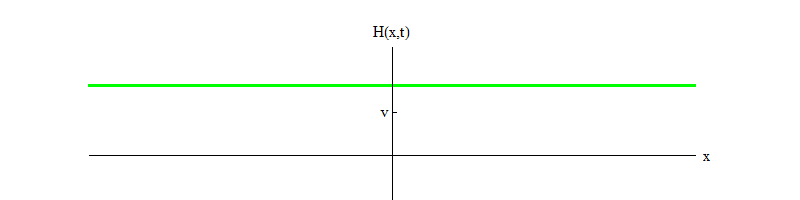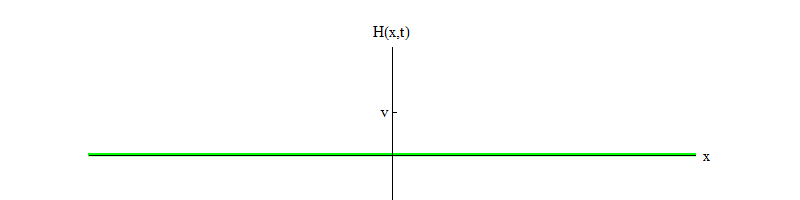Abb. 3

Mit der Zeit werden die Schwingungen aufgrund der Bedingungen der Bewegungsgleichung, die ich der Kürze halber weggelassen habe, verblassen. Sie ermöglichen die Übertragung eines Teils der Energie der Schwingungen des Feldes H auf Wellen anderer Felder (dies sind dieselben nichtlinearen Terme, mit denen Higgs-Teilchen zerfallen können ). Mit der Zeit (Abb. 4) beruhigt sich das Feld H in der Position H = v.

Bild

Abb. 4

Wenn ein physikalischer Prozess das Feld in einem kleinen Raumbereich von der Position H = v stößt, sendet das Feld Wellen der Form aus

H = v + A c o s [2 p i (n u t - x / l a m b d a)]

$H = v + A cos [2 \ pi (\ nu t - x / \ lambda)]$

Wobei A die Wellenamplitude ist, ν und λ ihre Frequenz und Wellenlänge sind und die Beziehung zwischen ν und λ von der genauen Form der Bewegungsgleichung abhängt, insbesondere von b und v. Und die Quanten dieser Wellen werden die Higgs-Teilchen sein. Frage pro Million: Wie groß ist die Masse des Higgs-Teilchens? Um dies zu berechnen, müssen wir, wie es immer für Teilchen erforderlich ist (die Wellenquanten in relativistischen Feldern darstellen), die Beziehung zwischen der Frequenz ν und der Wellenlänge λ der Wellen des entsprechenden Feldes bestimmen und dann das Ergebnis mit der Planck-Konstante h multiplizieren, um das Verhältnis zwischen der Energie zu erhalten und den Quantenimpuls dieser Wellen, der uns die Masse des Quanten (d. h. Teilchen) sagt.

Genau das machen wir mit dem im ersten Artikel erwähnten Feld S (x, t). Wir schreiben eine verschobene Version des Higgs-Feldes, drücken es als H (x, t) = v + h (x, t) aus und setzen dies in die Bewegungsgleichung des Feldes H ein. H (x, t) Ich werde fett schreiben, um es zu unterscheiden aus Plancks Konstante h. In dem im Übersichtsartikel angegebenen Beispiel für das Feld S ist eine einfache Bewegungsgleichung angegeben, sodass die Verschiebung die Masse des Partikels S nicht verändert hat. In diesem Fall ist dies jedoch nicht der Fall! Die Higgs-Feldbewegungsgleichung ist komplexer, daher unterscheidet sich die Gleichung für h stark von der ursprünglichen Gleichung für H:

d^{2} t e x t b f h / d t^{2} - c^{2} d^{2} t e x t b f h / d x^{2} = - b^{2} (v + t e x t b f h) (2 v t e x t b f h + t e x t b f h^{2})

$d ^ 2 \ textbf {h} / dt ^ 2 - c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 = - b ^ 2 (v + \ textbf {h}) (2 v \ textbf {h} + \ textbf {h} ^ 2)$

Wo ich die Tatsache verwendet habe, dass v eine Konstante ist und unabhängig von Raum und Zeit ist. Dann erinnern wir uns, dass das Higgs-Feldquant eine kleine Amplitude hat. Wenn wir also das einzige Higgs-Teilchen untersuchen (was genau das ist, was wir zur Bestimmung seiner Masse benötigen), können wir alle Terme verwerfen, die proportional zu h ² und h ^{3 sind} :

d^{2} t e x t b f h / d t^{2} - c^{2} d^{2} t e x t b f h / d x^{2} = - 2 b^{2} v^{2} t e x t b f h + . . .

$d ^ 2 \ textbf {h} / dt ^ 2 - c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 = - 2 b ^ 2 v ^ 2 \ textbf {h} + ...$

Wobei "+ ..." abgelegte Mitglieder zurückruft. Beachten Sie, dass diese Gleichung für h (x, t) zur Klasse 1 gehört, obwohl wir mit einer Gleichung der Klasse -1 für H (x, t) begonnen haben. Dies liegt daran, dass H (x, t) im Bereich von H = 0 instabil war und h (x, t) im Bereich von h = 0 stabil war, wobei H = v. Wir können also die Masse m _{h des} Higgs-Teilchens h unter Verwendung der folgenden Form einer Gleichung der Klasse 1 berechnen:

m_{h} = s q r t 2 (h / 2 p i) b v / c^{2}

$m_h = \ sqrt2 (h / 2 \ pi) b v / c ^ 2$

h auf der rechten Seite bezeichnet die Planck-Konstante. Wenn sich herausstellt, dass das Higgs-ähnliche Teilchen, das kürzlich auf dem LHC gefunden wurde, wirklich das Higgs-Teilchen des Standardmodells ist, können wir zum ersten Mal herausfinden, was b ist (denken Sie daran, dass v wir bereits vor langer Zeit kannten) und schließlich den Wert a = b herausfinden v.

v = 246 GeV;
m _h ≈ 125 GeV / c² (wenn das neue Teilchen Higgs ist)
b ≤ 0,35 (2 π / h) (wenn das neue Teilchen das Higgs des Standardmodells ist)
a = bv ≈ 87 GeV (2 π / h) (wenn das neue Teilchen das Higgs des Standardmodells ist)

wobei h wiederum die Plancksche Konstante ist. Und die letzten drei Größen waren uns bis zur jüngsten Entdeckung des Higgs-Teilchens nicht bekannt.

Wenn sich nun herausstellt, dass das Standardmodell nicht der Natur entspricht (wenn zusätzlich zu H (x, t) zusätzliche Felder zu den bekannten Feldern hinzugefügt werden müssen, um die Eigenschaften eines kürzlich entdeckten Partikels mit einer Masse von 125 GeV / c² zu erklären), nehmen wir an, dass dieses Partikel eines von mehreren ist Arten von Higgs-Partikeln - dann müssen wir uns noch einige Jahre mit dieser schwierigen Situation auf dem LHC auseinandersetzen. Sie können sich viele Möglichkeiten vorstellen, und es macht keinen Sinn, sie Ihnen allen zu erklären, aber ich habe hier einige davon grob beschrieben. und wenn die am LHC eingegangenen Daten uns eine bestimmte Richtung zeigen, werde ich Ihnen alles im Detail erklären.

Wie funktioniert das Higgs-Feld: 3) Wie erscheint das Higgs-Teilchen?

More articles: