Die klassische Mechanik ist intuitiv: Sie wird täglich und wiederholt von Menschen zum Überleben verwendet. Aber bis zum zwanzigsten Jahrhundert hatte noch niemand die Quantenmechanik benutzt. Sie beschreibt Dinge, die so klein sind, dass sie völlig aus der Wahrnehmung der menschlichen Sinne herausfallen. Der einzige Weg, diese Theorie zu verstehen und ihre Schönheit zu genießen, besteht darin, unsere Intuition mit abstrakter Mathematik zu blockieren.
Leonard Sasskind - ein berühmter amerikanischer Wissenschaftler - lädt Sie zu einer aufregenden Reise in das Land der Quantenmechanik ein. Unterwegs benötigen Sie Grundkenntnisse aus dem Schulphysikkurs sowie die Grundlagen der mathematischen Analyse und der linearen Algebra. Sie müssen auch etwas über die Themen wissen, die in Susskinds erstem Buch „Theoretisches Minimum“ angesprochen wurden - „Alles, was Sie über moderne Physik wissen müssen“. Aber es ist furchtlos, wenn dieses Wissen etwas vergessen wird. Viele Autoren werden auf dem Weg daran erinnern und erklären.
Die Quantenmechanik ist eine ungewöhnliche Theorie: Nach ihren Postulaten können wir beispielsweise alles über das System und nichts über seine Einzelteile wissen. Einstein und Niels Bohr diskutierten viel über diesen und andere Widersprüche. Wenn Sie keine Angst vor Schwierigkeiten haben, einen forschenden Geist haben, technisch kompetent, aufrichtig und tief an Physik interessiert sind, dann wird Sie dieser Kurs von Leonard Sasskind ansprechen. Das Buch konzentriert sich auf die logischen Prinzipien der Quantentheorie und zielt nicht darauf ab, das Paradoxon der Quantenlogik zu glätten, sondern es ans Tageslicht zu bringen und zu versuchen, mit den schwierigen Fragen umzugehen, die es aufwirft.
Wellenfunktionsübersicht
In dieser Vorlesung werden wir die Sprache der Wellenfunktionen verwenden. Lassen Sie uns daher vor dem Tauchen einen kurzen Überblick über das Material geben. In Vorlesung 5 haben wir die Wellenfunktionen abstrakter Objekte diskutiert, ohne zu erklären, wie sie sich auf Wellen oder Funktionen beziehen. Bevor ich diese Lücke fülle, erinnere ich Sie an das, was wir zuvor besprochen haben.
Zunächst wählen wir ein beobachtbares L mit Eigenwerten l und Eigenvektoren | l〉. Sei | Y〉 ein Zustandsvektor. Da die Eigenvektoren des Hermitianischen Operators eine vollständige orthonormale Basis bilden, kann der Vektor | Y〉 auf dieser Basis erweitert werden:
Wie Sie sich aus den Abschnitten 5.1.2 und 5.1.3 erinnern, werden die Größen Y (l) als Wellenfunktion des Systems bezeichnet. Beachten Sie jedoch: Die spezifische Form von Y (l) hängt von dem spezifischen beobachtbaren L ab, das wir ursprünglich ausgewählt haben. Wenn wir eine andere beobachtbare Größe wählen, wird sich die Wellenfunktion (zusammen mit den Basisvektoren und Eigenwerten) als unterschiedlich herausstellen, obwohl wir immer noch über denselben Zustand sprechen. Daher müssen wir reservieren, dass Y (l) die mit | Yñ verbundene Wellenfunktion ist. Um genau zu sein, müssen wir sagen, dass Y (l) die Wellenfunktion in der L-Basis ist. Wenn wir die Orthonormalitätseigenschaften dieser Basis von Vektoren 〈li | lj〉 = dij verwenden, kann die Wellenfunktion in dieser L-Basis auch unter Verwendung der internen Produkte (oder Projektionen) des Zustandsvektors | Y〉 durch die Eigenvektoren | l〉: Y (l) definiert werden ) = 〈L | Y〉
Es gibt zwei Möglichkeiten, über die Wellenfunktion nachzudenken. Zuallererst ist dies eine Menge von Komponenten des Zustandsvektors auf einer bestimmten Basis. Diese Komponenten können in Form eines Spaltenvektors geschrieben werden:
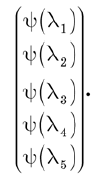
Eine andere Möglichkeit, über die Wellenfunktion nachzudenken, besteht darin, sie als Funktion von l zu betrachten. Wenn Sie einen gültigen Wert von l festlegen, gibt die Funktion Y (l) eine komplexe Zahl an. Wir können also sagen, dass Y (l) eine komplexwertige Funktion der diskreten Variablen l ist. Mit dieser Überlegung werden lineare Operatoren zu Operationen, die für Funktionen gelten und neue Funktionen geben.
Und noch eine letzte Erinnerung: Die Wahrscheinlichkeit, dass das Experiment das Ergebnis l liefert, ist gleich P (l) = Y * (l) Y (l).
Funktionen und Vektoren
Bisher hatten die von uns untersuchten Systeme endlichdimensionale Zustandsvektoren. Zum Beispiel wird ein einfacher Spin durch einen zweidimensionalen Zustandsraum beschrieben. Aus diesem Grund hatten die Observablen nur eine endliche Anzahl möglicher beobachtbarer Werte. Es gibt jedoch komplexere Observablen, die unendlich viele Werte haben können. Ein Beispiel ist ein Partikel. Teilchenkoordinaten sind beobachtbar, aber im Gegensatz zum Spin haben Koordinaten eine unendliche Anzahl möglicher Werte. Beispielsweise kann sich ein Partikel, das sich entlang der x-Achse bewegt, an einer beliebigen Materialmarkierung x befinden. Mit anderen Worten, x ist eine stetige unendliche Variable. Wenn die beobachteten Systeme kontinuierlich sind, wird die Wellenfunktion zu einer vollwertigen Funktion der kontinuierlichen Variablen. Um die Quantenmechanik auf Systeme dieser Art anzuwenden, müssen wir das Konzept der Vektoren erweitern, um Funktionen darin aufzunehmen.
Funktionen sind Funktionen und Vektoren sind Vektoren; Sie scheinen völlig unterschiedliche Einheiten zu sein. In welchem Sinne sind also Funktionsvektoren? Wenn Sie sich Vektoren als Pfeile im dreidimensionalen Raum vorstellen, dann sind sie natürlich überhaupt nicht mit Funktionen identisch. Wenn Sie jedoch Vektoren breiter betrachten als mathematische Objekte, die einige Postulate erfüllen, bilden die Funktionen tatsächlich einen Vektorraum. Ein solcher Vektorraum wird zu Ehren des Mathematikers David Hilbert oft als Hilbert-Raum bezeichnet.
Betrachten Sie die Menge der komplexen Funktionen Y (x) einer reellen Variablen x. Mit einer komplexen Funktion meine ich, dass jedem x eine komplexe Zahl Y (x) zugeordnet ist. Die unabhängige Variable x ist andererseits eine gewöhnliche reelle Variable. Es können beliebige reelle Werte von –∞ bis + ∞ angenommen werden.
Jetzt geben wir genau an, was wir damit meinen, dass „Funktionen Vektoren sind“. Dies ist keine oberflächliche Analogie oder Metapher. Unter einigen Einschränkungen (auf die wir später zurückkommen werden) erfüllen Funktionen wie Y (x) die mathematischen Axiome, die einen Vektorraum definieren. Wir haben diese Idee in Abschnitt 1.9.2 kurz erwähnt und verwenden sie nun in vollem Umfang. Wenn wir auf die Axiome eines komplexen Vektorraums zurückblicken (in Abschnitt 1.9.1), sehen wir, dass komplexe Funktionen sie alle erfüllen.
1. Die Summe von zwei beliebigen Funktionen ist eine Funktion.
2. Das Hinzufügen von Funktionen ist kommutativ.
3. Das Hinzufügen von Funktionen ist assoziativ.
4. Es gibt eine eindeutige Nullfunktion, so dass beim Hinzufügen zu einer Funktion dieselbe Funktion erhalten wird.
5. Für jede gegebene Funktion Y (x) gibt es eine eindeutige Funktion –Y (x), so dass Y (x) + (–Y (x)) = 0 ist.
6. Die Multiplikation einer Funktion mit einer komplexen Zahl ergibt eine Funktion und ist linear.
7. Die Verteilungseigenschaft wird beobachtet, was bedeutet, dass
z [Y (x) + j (x)] = zY (x) + zj (x),
[z + w] Y (x) = zY (x) + wY (x),
wobei z und w komplexe Zahlen sind.
All dies impliziert, dass wir die Funktion Y (x) mit dem Ket-Vektor | Y〉 im abstrakten Vektorraum identifizieren können. Es ist nicht überraschend, dass wir auch Bra-Vektoren definieren können. Der dem Kumpel sal | Y corresponding entsprechende BH-Vektor 〈Y | wird mit der komplexen Konjugatfunktion Y * (x) identifiziert.
Um diese Idee effektiv zu nutzen, müssen wir einige Objekte aus unseren mathematischen Werkzeugen verallgemeinern. In früheren Vorlesungen waren Bezeichnungen, die Wellenfunktionen identifizierten, Mitglieder einer endlichen diskreten Menge, beispielsweise die Eigenwerte einer bestimmten beobachtbaren Menge. Aber jetzt ist die unabhängige Variable stetig. Dies bedeutet unter anderem, dass wir es nicht mit normalen Beträgen zusammenfassen können. Ich denke du weißt was zu tun ist. Hier finden Sie funktionsorientierte Substitute für unsere drei Vektorkonzepte, von denen Sie zwei bereits kennen.
• Beträge werden durch Integrale ersetzt.
• Wahrscheinlichkeiten werden durch Wahrscheinlichkeitsdichten ersetzt.
• Das Kronecker-Delta-Symbol wird durch die Dirac-Delta-Funktion ersetzt.
Schauen wir uns diese Tools genauer an.
Beträge werden durch Integrale ersetzt . Wenn wir wirklich die Genauigkeit beibehalten wollten, würden wir zunächst die x-Achse durch einen diskreten Satz von Punkten ersetzen, die durch sehr kleine Intervalle ε getrennt sind, und dann zur Grenze ε → 0 übergehen. Es würde mehrere Seiten dauern, um jeden Schritt zu rechtfertigen. Aber wir können diesen Ärger mit ein paar intuitiven Definitionen vermeiden, wie zum Beispiel das Ersetzen von Summen durch Integrale. Schematisch kann dieser Ansatz wie folgt geschrieben werden:
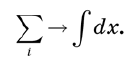
Wenn Sie beispielsweise die Fläche unter der Kurve berechnen müssen, wird die x-Achse in winzige Segmente unterteilt, und die Flächen einer großen Anzahl von Rechtecken werden wie bei einer elementaren mathematischen Analyse addiert. Wenn wir die Segmente auf die Größe Null zusammenziehen lassen, wird die Summe zu einem Integral.
Betrachten Sie die Klammer 〈Y | und ket | Y〉 und definieren ihr inneres Produkt. Der naheliegende Weg, dies zu tun, besteht darin, die Summation in Gleichung (1.2) durch Integration zu ersetzen. Wir definieren das innere Produkt wie folgt:
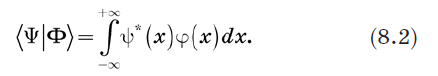Wahrscheinlichkeiten werden durch Wahrscheinlichkeitsdichten ersetzt . Als nächstes identifizieren wir P (x) = Y * (x) Y (x) mit der Wahrscheinlichkeitsdichte für die Variable x. Warum mit Wahrscheinlichkeitsdichte und nicht nur mit Wahrscheinlichkeit? Wenn x eine stetige Variable ist, ist die Wahrscheinlichkeit, dass ein genau gegebener Wert angenommen wird, normalerweise Null. Daher ist es richtiger, die Frage so zu stellen: Wie groß ist die Wahrscheinlichkeit, dass x zwischen zwei Werten x = a und x = b liegt? Die Wahrscheinlichkeitsdichte wird so bestimmt, dass diese Wahrscheinlichkeit durch das Integral gegeben ist
Da die Gesamtwahrscheinlichkeit 1 sein muss, können wir die Normalisierung des Vektors als definieren
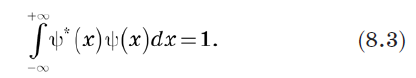Das Kronecker-Delta-Symbol wird durch die Dirac-Delta-Funktion ersetzt . Bisher war alles sehr vertraut. Die Dirac Delta Funktion ist etwas Neues. Die Delta-Funktion ist ein Analogon des Kronecker-Delta-Symbols dij, das per Definition 0 ist, wenn i ≠ j ist, und 1, wenn i = j. Es kann aber auch anders definiert werden. Betrachten Sie einen beliebigen Vektor Fi in einem endlichdimensionalen Raum. Es ist leicht zu erkennen, dass das Kronecker-Delta-Symbol die Bedingung erfüllt
Dies liegt daran, dass nur Terme mit j = i in dieser Summe ungleich Null sind. Während der Summierung filtert das Kronecker-Symbol alle Komponenten von F außer Fi heraus. Eine naheliegende Verallgemeinerung besteht darin, eine neue Funktion zu definieren, die bei Verwendung unter dem Integral dieselbe Filtereigenschaft aufweist. Mit anderen Worten, wir brauchen eine neue Entität d (x - x '), die die Eigenschaft hat, dass für jede Funktion F (x)
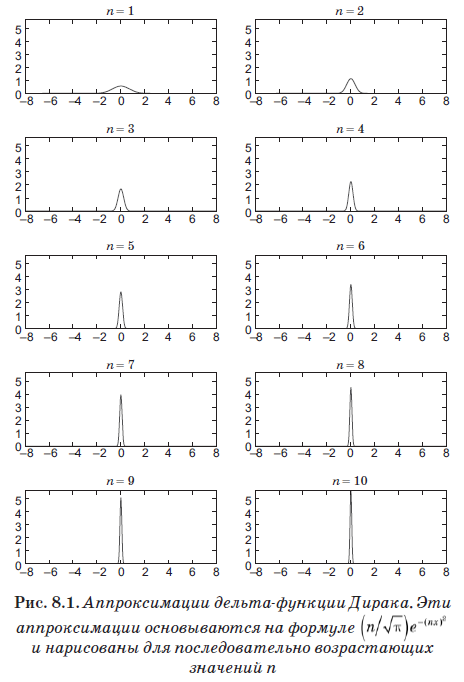
Gleichung (8.4) definiert eine neue Entität namens Dirac-Delta-Funktion, die sich als das wichtigste Werkzeug in der Quantenmechanik herausstellte. Aber trotz seines Namens ist dies nicht wirklich eine Funktion im üblichen Sinne. Es ist gleich Null, wobei x ≠ x 'ist, aber wenn x = x' ist, geht es ins Unendliche. Tatsächlich ist es gerade so unendlich, dass die Fläche unter d (x) gleich 1 ist. Grob gesagt ist diese Funktion im unendlich kleinen Intervall ε ungleich Null, aber in diesem Intervall hat sie den Wert 1 / ε. Somit ist die Fläche darunter gleich 1 und erfüllt, was noch wichtiger ist, Gleichung (8.4). Funktion
nähert sich der Delta-Funktion für sehr große Werte von n recht gut an. In Abb. 8.1 zeigt diese Optimierung mit steigenden Werten von n. Trotz der Tatsache, dass wir uns für n = 10 entschieden haben, dh einen sehr kleinen Wert, ist zu beachten, dass der Graph bereits zu einem sehr engen und scharfen Peak geworden ist.
»Weitere Informationen zum Buch finden Sie auf
der Website des Herausgebers»
Inhalt»
AuszugFür Leser dieses Blogs 20% Rabatt auf den Gutschein -
Sasskind