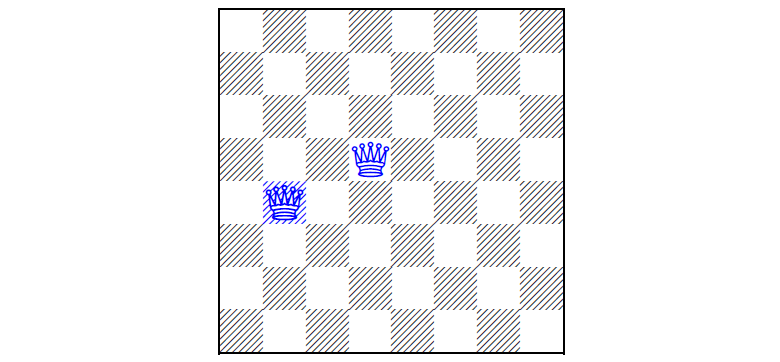
Die erste Version des Puzzles aus dem Jahr 1850, bei der zwei Königinnen auf dem Brett vorinstalliert sind und der Spieler die verbleibenden Königinnen anordnen muss (zwei Lösungen für das Problem finden Sie unter dem Schnitt).Die Aufgabe von N Königinnen besteht darin, N Königinnen auf einem N × N-Brett zu platzieren, so dass sich keine Königin im Kampf der anderen befindet und mehrere Königinnen auf dem Brett vorinstalliert sind. Das heißt, am Ende sollten sich keine zwei Königinnen auf derselben Linie oder Diagonale befinden. Das Problem wurde erstmals 1848 formuliert, und 1850 wurde eine Puzzle-Variante entwickelt, bei der eine bestimmte Anzahl von Königinnen im Voraus auf das Brett gelegt wurde und der Spieler den Rest nach Möglichkeit arrangieren sollte.
Forscher der St. Andrews University (Schottland) haben einen
wissenschaftlichen Artikel veröffentlicht, der belegt, dass das N-Queens-Problem nicht nur # P-vollständig, sondern auch NP-vollständig ist. Darüber hinaus ist das Clay Institute of Mathematics (USA) bereit, eine Million Dollar an jeden zu zahlen, der die Lösung dieses Problems als Beweisproblem P = NP optimieren kann.
Wie Sie wissen, ist #P in der Komplexitätstheorie eine Klasse von Problemen, deren Lösung die Anzahl der erfolgreichen ist, dh das Vervollständigen von Rechenpfaden für einige nicht deterministische Turing-Maschinen, die in Polynomzeit arbeiten. Die Rechenprobleme der Klasse #P (Zählprobleme) hängen mit den entsprechenden Entscheidungsproblemen der Klasse NP zusammen.
Wissenschaftler bemerken, dass diese Aufgabe die einfachste unter NP-vollständigen Aufgaben sein kann, um jedem, der die Regeln des Schachspiels kennt, das Wesentliche dieser Probleme zu erklären. Diese Aufgabe hat eine sehr interessante Geschichte. Zu einer Zeit erregte sie die Aufmerksamkeit von Gauß, der sogar einen kleinen Fehler in ihrer Entscheidung machte (im 8 × 8-Vorstand meldete er 76 Entscheidungen, erkannte dann aber vier davon als fehlerhaft, so dass nur noch 72 übrig waren, und später stellte Gauß alle 92 Entscheidungen fest für eine Tafel 8 × 8).
Eine Verallgemeinerung des Problems für das N × N-Board hat die Aufmerksamkeit vieler Mathematiker auf sich gezogen. Im Laufe des letzten halben Jahrhunderts wurden mehrere Dutzend wissenschaftliche Arbeiten veröffentlicht, die sich diesem Problem widmen. Mindestens sechs von ihnen werden in Google Scholar mehr als 400 Mal zitiert: Dies ist Golomb & Baumert, 1965; Bitner & Reingold, 1975; Mackworth & Freuder, 1985; Minton, Johnston, Philips & Laird, 1992; Selman, Levesque & Mitchell, 1992; Crawford, Ginsberg, Luks & Roy, 1996.
Die Komplexität des N-Queens-Problems wird oft falsch eingeschätzt. Selbst in reichlich zitierten Werken wird es oft als NP-hartes Problem (NP-hart) bezeichnet, aber es wird nur so sein, wenn P = NP. Tatsächlich ist die rechnerische Version des Problems,
dh die Bestimmung der Anzahl von Lösungen für N Königinnen, eine
Sequenz A000170 aus der Online-Enzyklopädie der ganzzahligen Sequenzen. Diese Sequenz ist nun maximal für n = 27 bekannt, wobei die Anzahl der Lösungen 2,34 × 10
17 überschreitet. Es ist keine effektivere Lösung für das Problem bekannt als eine einfache umfassende Suche. Für n = 27 im Jahr 2016 wurde daher eine groß angelegte parallele Suche auf FPGA verwendet.
Wenn der Computer beginnt, die möglichen Positionen von Königinnen auf einer 1000 × 1000-Zellenplatine aufzulisten, wird diese Aufgabe gleichzeitig für immer geladen. Laut Wissenschaftlern kann jemand, der einen wirklich schnellen und effektiven Weg findet, um das Problem zu lösen, vom Clay Institute of Mathematics viel mehr als eine Million Dollar davon profitieren. „Wenn Sie ein Programm schreiben, das das Problem sehr schnell lösen kann, können Sie es anpassen, um viele wichtige Aufgaben zu lösen, denen wir uns täglich stellen müssen“, sagt der Informatikprofessor Ian Gent, einer der Autoren der wissenschaftlichen Arbeit. "Dazu gehören triviale Probleme wie das Finden der größten Gruppe Ihrer Freunde auf Facebook, die sich nicht kennen, oder sehr wichtige Aufgaben, z. B. das Brechen von Codes, die die Sicherheit aller unserer Online-Transaktionen gewährleisten."
Dies sind jedoch rein theoretische Erfindungen. In der Praxis hat sich noch niemand schnell und effektiv der Lösung des Problems der N Königinnen genähert. Für den Beweis, dass es einen effektiveren Weg gibt, das Problem zu lösen, als eine einfache Aufzählung aller Optionen, geben sie eine Million Dollar.
Ein wissenschaftlicher Artikel wurde im August 2017 in der Zeitschrift
Journal of Artificial Intelligence Research (doi: 10.1613 / jair.5512,
pdf ) veröffentlicht.
PS Zwei Lösungen für das Problem mit KDPV:
