Das Buch „Theoretisches Minimum. Alles, was Sie über moderne Physik wissen müssen “

„Theoretisches Minimum“ ist ein Buch für diejenigen, die den Physikunterricht in Schule und Institut verpasst haben, es aber bereits bereuen. Möchten Sie die Grundlagen der Naturwissenschaften verstehen und lernen, wie moderne Physiker zu denken und zu argumentieren? In origineller und nicht standardmäßiger Form bieten die berühmten amerikanischen Wissenschaftler Leonard Sasskind und George Grabowski einen Einführungskurs in Mathematik und Physik für Neugierige an.

Im Gegensatz zu anderen populärwissenschaftlichen Büchern, die versuchen, die Gesetze der Physik auf zugängliche Weise zu erklären und dabei Gleichungen und Formeln geschickt zu vermeiden, lehren die Autoren den Leser die klassischen Grundlagen der Naturwissenschaften. Das Buch bietet eine eigene originelle Lehrmethode, ergänzt durch Videovorträge, die auf theoretischminimum.com veröffentlicht wurden .

Vorlesung 9. Phasenflüssigkeit und der Gibbs-Liouville-Satz

Lenny schaute gern auf den Fluss, besonders um die kleinen Flecken auf der Oberfläche zu beobachten. Er versuchte sich vorzustellen, wie sie sich zwischen Steinen bewegen oder in Strudel fallen würden. Aber der Flusslauf als Ganzes - die kombinierte Bewegung eines großen Wasservolumens mit Strömen, die sich trennen, zusammenlaufen und überholen - war für ihn unverständlich.

Phasenflüssigkeit

Für die klassische Mechanik ist es sehr natürlich, sich auf bestimmte Anfangsbedingungen zu konzentrieren und einer separaten Flugbahn im Phasenraum zu folgen. Es gibt aber auch eine breitere Sichtweise, die eine ganze Familie von Flugbahnen abdeckt. Anstatt die Spitze des Bleistifts an einer bestimmten Stelle im Phasenraum zu platzieren und den einzigen Weg von dort aus zu verfolgen, werden wir versuchen, etwas ehrgeizigeres zu tun. Stellen Sie sich vor, wir haben unendlich viele Stifte und verwenden sie so, dass wir den Phasenraum gleichmäßig mit Punkten füllen (durch Homogenität meine ich, dass die Dichte der Punkte im Raum q, p überall gleich ist). Betrachten Sie diese Punkte als Partikel, die eine imaginäre Flüssigkeit bilden, die den Phasenraum füllt.

Lassen Sie nun jeden Punkt gemäß den Hamiltonschen Bewegungsgleichungen bewegen:


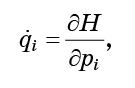
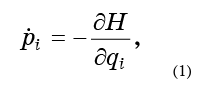
so dass unsere Flüssigkeit endlos durch den Phasenraum fließt.

Ein harmonischer Oszillator ist ein gutes erstes Beispiel. In Vorlesung 8 haben wir gesehen, dass sich jeder Punkt in einer Kreisbahn mit konstanter Winkelgeschwindigkeit bewegt. (Ich möchte Sie daran erinnern, dass es sich um eine Phase handelt, nicht um einen Koordinatenraum. In der Koordinate bewegt sich der Oszillator in einer Dimension hin und her.) Die gesamte Flüssigkeit als Ganzes macht eine feste Bewegung und dreht sich gleichmäßig um den Ursprung des Phasenraums.

Nun zurück zum allgemeinen Fall. Wenn die Anzahl der Koordinaten N ist, sind der Phasenraum und die Flüssigkeit darin 2N-dimensional. Die Flüssigkeit fließt, aber auf sehr spezifische Weise. Sein Fluss hat besondere Eigenschaften. Eine davon ist, dass wenn ein Punkt mit einer bestimmten Energie beginnt, dh für einen gegebenen Wert von H (q, p), dieser Energiewert gespeichert wird. Die Oberflächen konstanter Energie (zum Beispiel mit einer Energie gleich E) werden durch die Gleichung H (q, p) = E bestimmt. (2)

Für jeden Wert von E haben wir eine Gleichung mit 2N Phasenraumvariablen, die eine Oberfläche der Dimension 2N - 1 definiert. Mit anderen Worten, jeder Wert von E hat seine eigene Oberfläche; Wenn Sie alle E-Werte durchgehen, füllen diese Flächen den gesamten Phasenraum. Wir können den Phasenraum mit den durch Gleichung (2) gegebenen Flächen als Konturkarte (Abb. 1) betrachten, auf der die Horizontalen nicht die Höhe, sondern die Energiewerte darstellen. Wenn sich der Flüssigkeitspunkt auf einer bestimmten Oberfläche befindet, bleibt er für immer darauf. Dies ist das Gesetz der Energieerhaltung.

Der Phasenraum des harmonischen Oszillators ist zweidimensional und die Energieoberflächen sind Kreise:

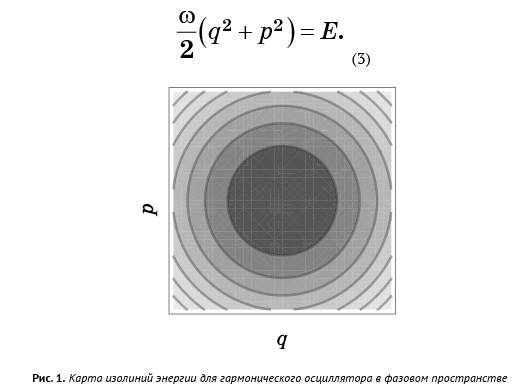
Im allgemeinen Fall sind die Energieoberflächen eines mechanischen Systems zu kompliziert, um sie zu visualisieren, aber das Prinzip bleibt dasselbe: Energieoberflächen füllen den Phasenraum als Schichten, und die Strömung bewegt sich so, dass die Punkte auf der Oberfläche verbleiben, auf der sie ursprünglich waren .

Kurze Erinnerung

Ich möchte hier anhalten und mich an das erinnern, was in der allerersten Vorlesung gesagt wurde, in der Münzen, Würfel und die einfachsten Ideen zu den Bewegungsgesetzen besprochen wurden. Wir haben diese Gesetze mit einer Reihe von Pfeilen beschrieben, die die Punkte verbinden, die die Zustände des Systems darstellen. Wir haben auch erklärt, dass Gesetze zulässig und unzulässig sind, während zulässige umkehrbar sind. Die Quintessenz ist, dass jeder Punkt genau einen eingehenden Pfeil und genau einen ausgehenden Pfeil haben muss. Wenn mindestens an einem Punkt die Anzahl der eingehenden Pfeile die Anzahl der ausgehenden Pfeile überschreitet (dies wird als Konvergenz bezeichnet), ist ein solches Gesetz irreversibel. Gleiches gilt für den Fall, dass mehr ausgehende als eingehende Pfeile vorhanden sind (dies wird als Divergenz bezeichnet). Sowohl die Divergenz als auch die Konvergenz von Pfeilen verletzen die Reversibilität und sind verboten. Bisher sind wir nicht zu dieser Argumentation zurückgekehrt. Jetzt ist die Zeit gekommen.

Fluss und Divergenz

Betrachten Sie einige einfache Beispiele für den Flüssigkeitsfluss im normalen Raum. Für einen Moment vergessen wir den Phasenraum und betrachten nur eine gewöhnliche Flüssigkeit, die sich im üblichen dreidimensionalen Raum mit den als x, y, z bezeichneten Achsen bewegt. Die Strömung kann durch das Geschwindigkeitsfeld beschrieben werden. Geschwindigkeitsfeld

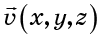
wird durch Einstellen des Geschwindigkeitsvektors an jedem Punkt im Raum bestimmt (Abb. 2).

Sie können das Geschwindigkeitsfeld auch mit Geschwindigkeitskomponenten beschreiben:

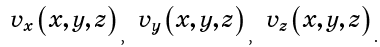
Auch die Geschwindigkeit an einem Punkt kann von der Zeit abhängen, aber nehmen wir an, dass es keine solche Abhängigkeit gibt. In diesem Fall wird die Strömung als stationär bezeichnet .

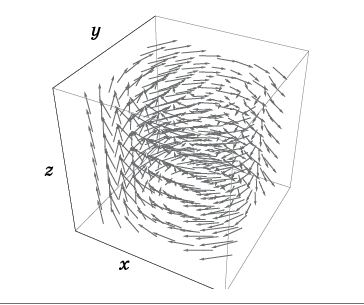
Abb. 2. Geschwindigkeitsfeld

nimmt den gleichen Betrag. Dies bedeutet auch, dass die Dichte einer Flüssigkeit - die Anzahl der Moleküle pro Volumeneinheit - überall gleich ist und über die Zeit konstant bleibt. Der Begriff "Inkompressibilität" bedeutet übrigens auch Unerweiterbarkeit. Mit anderen Worten, das Volumen der Flüssigkeit kann nicht zunehmen. Stellen Sie sich eine kleine kubische Zelle vor, die durch die Bedingungen definiert ist:

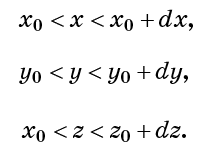
Inkompressibilität impliziert, dass die Anzahl der Fluidpunkte in jeder solchen Zelle konstant ist. Dies bedeutet auch, dass der gesamte Flüssigkeitsstrom, der in die Zelle eintritt (pro Zeiteinheit), Null sein muss. (Wie viele Punkte des Flusses eintreten, die gleiche Anzahl tritt aus.) Betrachten Sie die Anzahl der Moleküle, die pro Zeiteinheit durch die Zelloberfläche x = x0 fließen. Sie ist proportional zur Strömungsgeschwindigkeit auf dieser Oberfläche vx (x0).

Wenn die Geschwindigkeit vx bei x0 und bei x0 + dx gleich ist, ist der Fluss in die Zelle durch x = x0 der gleiche wie der Fluss von ihr durch x = x0 + dx. Wenn sich vx jedoch in der gesamten Zelle ändert, sind diese beiden Flüsse unausgeglichen. Der Gesamtfluss, der durch diese beiden Flächen in die Zelle fließt, ist proportional

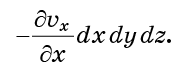
Genau die gleichen Überlegungen gelten für die Flächen y0 und y0 + dy sowie z0 und z0 + dz. Wenn alle hinzugefügt werden, dann der Gesamtfluss der Moleküle in die Zelle (Zufluss minus Abfluss)

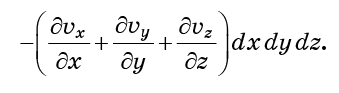
Die Kombination von Ableitungen in Klammern wird als Divergenz des Vektorfeldes bezeichnet
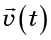
und ist bezeichnet

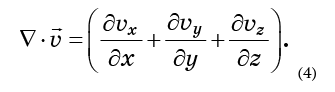
Die Divergenz spiegelt den Grad der Dispersion von Molekülen oder die Zunahme des von ihnen eingenommenen Volumens wider. Wenn die Flüssigkeit inkompressibel ist, sollte sich dieses Volumen nicht ändern, was bedeutet, dass die Divergenz Null sein sollte.

Eine Möglichkeit, Inkompressibilität zu verstehen, besteht darin, sich vorzustellen, dass jedes Molekül oder jeder Punkt ein Volumen einnimmt, das nicht verändert werden kann. Sie können nicht auf ein kleineres Volumen komprimiert werden, sie verschwinden nicht und erscheinen nicht aus dem Nichts. Mit ein wenig Nachdenken können Sie sehen, wie inkompressibel und reversibel ähnlich sind. In den Beispielen, die wir in Vorlesung 1 analysiert haben, haben die Pfeile auch eine Art Fluss bestimmt. Und im Wesentlichen war dieser Strom inkompressibel, zumindest wenn er reversibel war. Die natürliche Frage, die sich daraus ergibt, lautet: Ist der Fluss im Phasenraum reversibel? Die Antwort lautet ja, wenn das System die Hamilton-Gleichungen erfüllt. Und der Satz, der diese Inkompressibilität ausdrückt, heißt Liouville-Satz.

Liouville-Theorem

Kehren wir zum Fluidstrom im Phasenraum zurück und betrachten die Komponenten der Fluidgeschwindigkeit an jedem Punkt im Phasenraum. Es besteht keine Notwendigkeit zu sagen, dass das Phasenfluid in den Koordinaten x, y, z nicht dreidimensional ist. Es ist eine 2N-dimensionale Flüssigkeit in den Koordinaten pi, qi.

Somit gibt es 2N Komponenten des Geschwindigkeitsfeldes - eine für jede q-Koordinate und jede p-Koordinate. Lass sie

Das durch Gleichung (4) ausgedrückte Konzept der Divergenz lässt sich leicht auf eine beliebige Anzahl von Dimensionen verallgemeinern. In drei Dimensionen ist dies die Summe der Ableitungen der Geschwindigkeitskomponenten in den entsprechenden Richtungen. In gleicher Weise wird es für eine beliebige Anzahl von Dimensionen bestimmt. Im Fall des Phasenraums ist die Divergenz des Flusses die Summe von 2N Elementen:

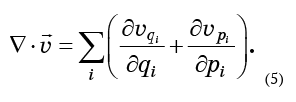
Wenn die Flüssigkeit inkompressibel ist, sollte dieser Ausdruck Null sein. Um es zu berechnen, müssen Sie die Komponenten des Geschwindigkeitsfeldes kennen - sie sind natürlich nichts anderes als die Geschwindigkeiten der Partikel des Phasenfluids.

Der Strömungsvektor an einem bestimmten Punkt wird mit der Geschwindigkeit eines imaginären Teilchens an diesem Punkt identifiziert. Mit anderen Worten

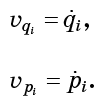
Darüber hinaus
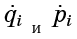
- Dies sind nur die Größen, die in die Hamilton-Gleichungen (1) eingegeben werden:


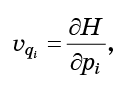
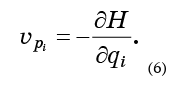
Alles, was getan werden muss, ist, die Gleichungen (6) in die Formel (5) einzusetzen und zu erhalten

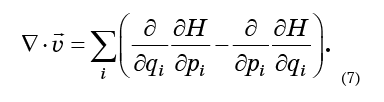
Daran erinnern, dass die zweite Ableitung der Form


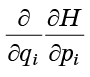
hängt nicht von der Reihenfolge der Differenzierung ab, wir werden verstehen, dass sich die Terme von Gleichung (7) genau paarweise gegenseitig zerstören:


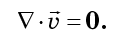
Das Phasenfluid ist also inkompressibel. In der klassischen Mechanik wird die Inkompressibilität einer Phasenflüssigkeit als Liouville-Theorem bezeichnet, obwohl sie fast keine Beziehung zum französischen Mathematiker Joseph Liouville hat. Es wurde erstmals 1903 vom großen amerikanischen Physiker Josiah Willard Gibbs veröffentlicht und ist auch als Gibbs-Liouville-Theorem bekannt.

Wir haben die Inkompressibilität einer Flüssigkeit bestimmt, indem wir gefordert haben, dass die Gesamtmenge an Flüssigkeit, die in eine kleine Zelle eintritt, Null ist. Es gibt eine andere streng äquivalente Definition. Stellen Sie sich zu einem bestimmten Zeitpunkt ein Flüssigkeitsvolumen vor. Dieses Volumen kann jede Form haben: kugelförmig, kubisch, tropfenartig - was auch immer. Jetzt werden wir die Bewegung aller Punkte dieses Bandes verfolgen. Nach einiger Zeit befindet sich ein Tropfen Flüssigkeit an einer anderen Stelle und hat eine andere Form. Wenn die Flüssigkeit jedoch inkompressibel ist, bleibt das Tröpfchenvolumen das gleiche wie ursprünglich. Wir können also den Satz von Liouville neu formulieren: Das Volumen, das ein Tropfen Phasenflüssigkeit einnimmt, bleibt zeitlich erhalten .

Betrachten Sie ein Beispiel eines harmonischen Oszillators, bei dem sich eine Flüssigkeit um einen Referenzpunkt dreht. Offensichtlich behält der Tropfen das Volumen bei, da seine gesamte Bewegung auf eine Festkörperrotation reduziert ist. Die Form des Tropfens bleibt unverändert, dies ist jedoch beim harmonischen Oszillator der Fall. Betrachten Sie ein anderes Beispiel. Angenommen, der Hamilton-Operator hat die Form H = pq.

Vielleicht erscheint Ihnen dies anders als der Hamiltonianer, obwohl es völlig richtig ist. Wir leiten die Bewegungsgleichungen ab:

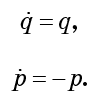
Nach diesen Gleichungen nimmt q mit der Zeit exponentiell zu und p nimmt mit der gleichen Geschwindigkeit exponentiell ab. Mit anderen Worten, die Strömung drückt das Fluid gegen die p-Achse und dehnt es gleichzeitig entlang der q-Achse in gleichem Maße aus. Jeder Tropfen erstreckt sich entlang q und zieht sich entlang p zusammen. Offensichtlich erfährt der Tropfen enorme Verformungen, aber sein Phasenvolumen ändert sich nicht.

Der Liouville-Satz ist das am nächsten vorstellbare Analogon der Art der Irreversibilität, die wir in Vorlesung 1 besprochen haben. In der Quantenmechanik wird der Liouville-Satz durch eine Quantenversion ersetzt, die als Einheitlichkeit bezeichnet wird. Die Unitarität ähnelt noch mehr dem, was wir in Vorlesung 1 besprochen haben, aber dies ist das Thema der nächsten Ausgabe von The Theoretical Minimum.

»Weitere Informationen zum Buch finden Sie auf der Website des Herausgebers
» Ausruf
» Auszug

Für Leser dieses Blogs 20% Rabatt auf den Gutschein - Theoretisches Minimum