Nachdem man Sand auf eine oszillierende elastische Platte gegossen hat, kann man die Bildung von Hladni-Figuren sehen . Sie dienen oft als Beispiel für die „natürliche Schönheit“ physikalischer Phänomene, obwohl hinter ihnen die eher einfache Physik der resonanten Anregung stehender Wellen steht. Und nur wenige Menschen achten auf das merkwürdige Merkmal dieser Figuren: Die Linien auf ihnen vermeiden Kreuzungen, als ob eine Kraft sie abstößt. Versuchen wir zu verstehen, welche Art von Physik hinter dieser Abstoßung verborgen ist und wie sie mit der Quantentheorie des Chaos zusammenhängt.

Stehende Wellen

Wie wir wissen, können elastische Körper ziemlich komplexe Schwingungen erzeugen, bei denen sie sich zusammenziehen, dehnen, biegen und verdrehen. Trotzdem können die Schwingungen eines elastischen Körpers als eine Kombination von einfacheren normalen Schwingungen dargestellt werden, die sich überlagern. So sehen mehrere normale Schwingungen eines einfachen elastischen Körpers - einer eindimensionalen gedehnten Schnur - aus.

Jede normale Schwingung wird durch eine stehende Welle dargestellt , die im Gegensatz zu einer Wanderwelle stillsteht und ein eigenes Muster für die Verteilung der Amplituden der Schwingungen im Raum aufweist. In dieser Figur können Antinoden unterschieden werden - Punkte, an denen die Schwingungsamplitude Maxima erreicht, und Knoten - feste Punkte, an denen die Schwingungsamplitude Null ist. Zusätzlich schwingt jede solche Welle mit ihrer eigenen Frequenz . Wie Sie sehen, nimmt bei einer Saite die Schwingungsfrequenz einer stehenden Welle mit zunehmender Anzahl von Knoten und Gegenknoten zu.


Betrachten wir nun ein zweidimensionales System, ein Beispiel dafür ist eine dünne elastische Membran, die über einen starren Rahmen gespannt ist. Normale Schwingungen einer runden Membran sehen komplizierter aus als bei einer Schnur, und anstelle einzelner Punktknoten gibt es Knotenlinien, entlang denen die Membran stationär ist.


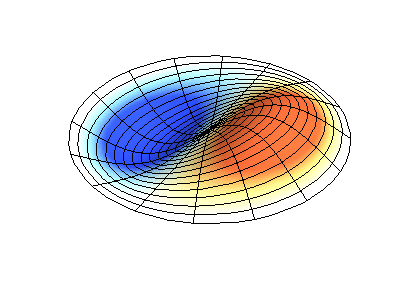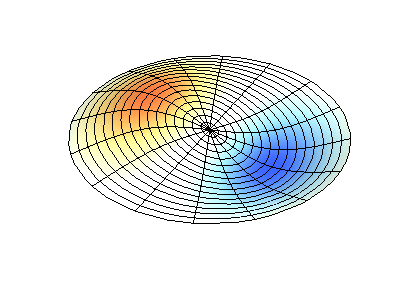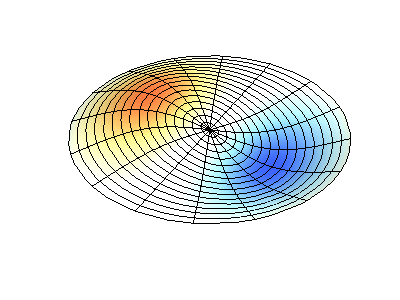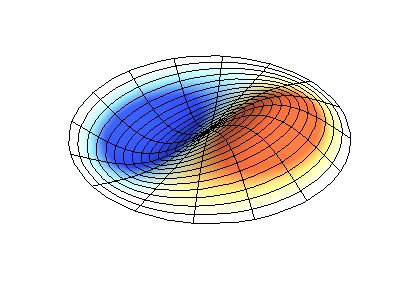
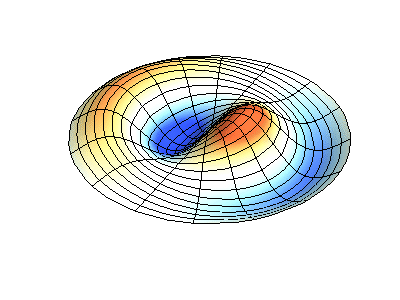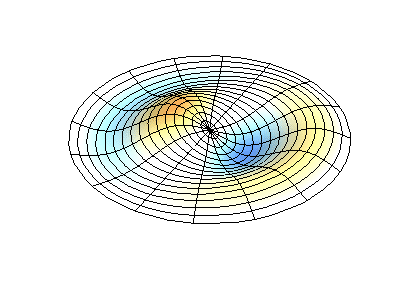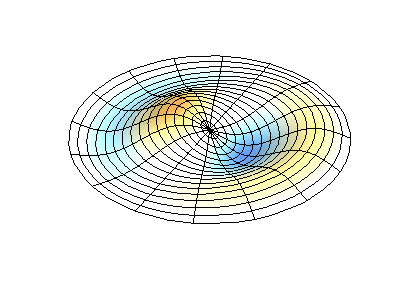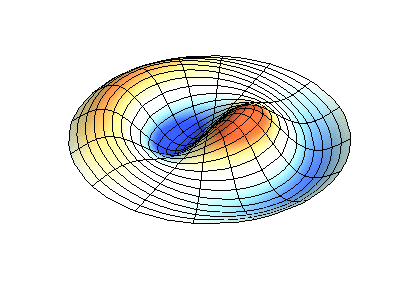
Normale Schwingungen einer runden Membran mit festen Kanten. Quelle


Grüne Farbe zeigt Knotenlinien.

Bei einer runden Membran können sich Knotenlinien, die Kreise und Segmente entlang der Radien sind, rechtwinklig schneiden. Wenn die Kanten der Membran eine beliebige Form haben, wird das Ermitteln der Frequenzen normaler Schwingungen und Muster ihrer Knoten und Gegenknoten zu einem Problem, das nur mit einem Computer gelöst werden kann.

Profile der Schwingungsamplitude stehender Wellen auf Membranen in Form eines Quadrats mit einem Loch , Koch-Schneeflocken und der Oberfläche eines Kätzchens .

Die Gleichungen, die die Schwingungen einer dünnen elastischen Platte beschreiben, unterscheiden sich von den Schwingungsgleichungen der Membran, da die Platte ihre eigene Steifigkeit aufweist, während die Membran nur aufgrund der Spannung durch äußere Kräfte weich und federnd ist. Es gibt jedoch auch Sätze normaler Schwingungen, deren Zeichnungen wesentlich von der Form der Grenzen abhängen.

Hladni Figuren

Wie oben erwähnt, sind Körperschwingungen im allgemeinen Fall eine Kombination eines ganzen Satzes normaler Schwingungen, die darin angeregt werden. Das Resonanzphänomen ermöglicht es Ihnen, eine der normalen Schwingungen, die wir benötigen, selektiv anzuregen. Dazu müssen wir den Körper mit einer externen Kraft mit einer Frequenz schwingen, die der Eigenfrequenz der normalen Schwingung entspricht.

Die beiden folgenden Videos zeigen ein typisches Schema zum Erhalten von Hladni-Figuren: Eine elastische Platte ist in der Mitte an einem Generator mechanischer Schwingungen angebracht, deren Frequenz allmählich zunimmt. Normale Plattenschwingungen mit ihren Knoten- und Gegenknotenmustern werden angeregt, wenn die Oszillatorfrequenz resonant mit den Eigenfrequenzen dieser Schwingungen übereinstimmt (die Eigenfrequenzen sind im Video in der unteren linken Ecke dargestellt).

Hier ist die Version desselben Videos, in der die Frequenzen normaler Vibrationen nach Gehör geschätzt werden können.

Und hier ist ein bisschen schöner.

Wir sehen Muster von Knoten und Gegenknoten aufgrund der Tatsache, dass Luftströme in der Nähe einer oszillierenden Platte Sandkörner zu den Knotenlinien einer stehenden Welle blasen ^(*) . So zeigen uns die Hladni-Figuren Muster von Knotenlinien normaler Schwingungen einer elastischen Platte.

Mehrere Hladni-Figuren auf dem Oberdeck der Gitarre. Quelle

Ein weiteres Beispiel für normale Wellen sind stehende Wellen auf der Wasseroberfläche. Sie werden durch eine Gleichung beschrieben, die sich von den Schwingungsgleichungen der Platten und Membranen unterscheidet, jedoch denselben qualitativen Gesetzen folgt, und mit ihrer Hilfe ist es möglich, Analoga der Hladni-Figuren zu erhalten.

Mikropartikel auf der Wasseroberfläche in Gefäßen verschiedener Formen. Die schwarze Linie zeigt eine Skala von 2 Millimetern. Quelle

Klassisches Chaos

Wir haben also gesehen, dass bei einer runden Membran die Knotenlinien theoretisch sind! - bemerkenswert schneiden sich gleichzeitig auf den Hladni-Figuren auf quadratischen oder komplexeren Platten, Knotenlinien vermeiden Schnittpunkte. Um den Grund für diese Muster zu verstehen, müssen wir einen kurzen Ausflug in die Theorie des Chaos machen.

Klassisches Chaos ist eine Eigenschaft mechanischer Systeme, die in einer extrem starken Abhängigkeit der Bewegungsbahn von Änderungen der Anfangsbedingungen besteht. Diese Beziehung wird auch als „ Schmetterlingseffekt “ bezeichnet. Ein anschauliches Beispiel für chaotisches Verhalten sind Versuche, das Wetter vorherzusagen: Das Gleichungssystem, das die Bewegung der Atmosphäre und der Ozeane beschreibt, ermöglicht aufgrund exponentiell zunehmender Fehler aufgrund kleiner Ungenauigkeiten in den Anfangsdaten keine ausreichend genaue Vorhersage über lange Zeiträume ^(**) .

Das Chaos-Phänomen wurde vom Meteorologen und Mathematiker Edward Lorenz offen und populär gemacht, der entdeckte, dass zwei Wettervorhersageberechnungen, die mit sehr engen Anfangsbedingungen begannen, anfangs fast nicht zu unterscheiden waren, aber irgendwann begannen sie radikal auseinander zu gehen.

Zwei Berechnungen von Edward Lorenz, ausgehend von engen Anfangswerten 0,506 und 0,506127. Quelle

Die einfachsten Systeme, an deren Beispiel es bequem ist, das Chaos zu untersuchen, sind Billard - Abschnitte einer ebenen Fläche, auf denen eine Kugel ohne Reibung rollen kann und die absolut elastisch von starren Wänden abprallt. Beim chaotischen Billard weichen die Flugbahnen des Balls, die zu Beginn geringfügige Unterschiede aufweisen, anschließend erheblich voneinander ab. Ein Beispiel für chaotisches Billard ist das unten gezeigte Sinai- Billard, ein rechteckiger Pool mit einem kreisförmigen Hindernis in der Mitte. Wie wir sehen werden, wird Billard gerade aufgrund dieses Hindernisses chaotisch.

Zwei exponentiell divergierende Ballbahnen im Sinai-Billard. Quelle

Integrierbare und chaotische Systeme

Mechanische Systeme, die nicht chaotisch sind, werden als integrierbar bezeichnet. Am Beispiel von Billard können Sie den Unterschied zwischen integrierbaren und chaotischen Systemen deutlich erkennen.

Rechteckiges und rundes Billard sind aufgrund ihrer symmetrischen Form integrierbar ^(***) . Die Bewegung des Balls in solchen Billard ist einfach eine Kombination von zwei unabhängigen periodischen Bewegungen. Bei rechteckigem Billard handelt es sich um Bewegungen mit horizontalen und vertikalen Sprüngen von den Wänden, und rundum handelt es sich um Bewegungen entlang des Radius und Winkelbewegungen in einem Kreis um die Mitte. Eine solche Bewegung ist leicht zu berechnen und zeigt kein chaotisches Verhalten.

Ballbahnen in integrierbarem Billard.

Billard mit einer komplexeren Form, die nicht so symmetrisch wie ein Kreis oder ein Rechteck ist, ist chaotisch ^(****) . Eines davon, das wir oben gesehen haben, ist das Sinai-Billard, bei dem die Symmetrie des Rechtecks ​​durch einen kreisförmigen Einschluss in der Mitte zerstört wird. Ebenfalls häufig in Betracht gezogen werden Billard "Stadion" und Billard in Form von Schnecken Pascal. Der Ball bewegt sich in chaotischem Billard auf sehr komplizierten Wegen und zerfällt nicht in einfachere periodische Bewegungen.

Die Flugbahn des Balles im chaotischen Billard "Stadion" und "Schnecke Pascal".

Hier kann man bereits vermuten, dass das Vorhandensein von Schnittpunkten zwischen den Linien in den Figuren von Hladni davon abhängt, ob die Platte die Form eines integrierbaren oder chaotischen Billards hat. Dies ist auf den Fotos unten deutlich zu sehen.

Runde Teller Hladni, die die Eigenschaften von integriertem Billard demonstrieren. Quelle

Demonstration der Eigenschaften des chaotischen Billards der Platte Hladni in Form eines Billardstadions, des Gehäuses der Geige und des Platzes, dessen Symmetrie durch eine runde Befestigung in der Mitte unterbrochen wird (analog zum Sinai-Billard). Quelle

Quantenchaos

Wie kann man verstehen, warum die Schnittpunkte zwischen Knotenlinien auf die Integrierbarkeit von Billard zurückzuführen sind? Dazu müssen wir uns der Quantentheorie des Chaos zuwenden und die Theorie des Chaos mit der Mechanik von Schwingungen und Wellen kombinieren. Wenn in der klassischen Mechanik der Ball im Billard als ein materieller Punkt beschrieben wird, der sich entlang einer bestimmten Flugbahn bewegt, dann wird seine Bewegung in der Quantenmechanik als Ausbreitung einer Welle beschrieben, die der Schrödinger-Gleichung folgt und von den Wänden des Billards reflektiert wird.

Phasen der Wellenausbreitung in Quantenbillard. Anfangs ist die Welle in einem runden Impuls konzentriert und bewegt sich von links nach rechts, dann breitet sie sich aus und reflektiert wiederholt von den Wänden. Quelle

Das gleiche in Form einer Animation, jedoch mit leicht unterschiedlichen Anfangsbedingungen.

Wie bei Schwingungen von Membranen und Platten ermöglicht die Schrödinger-Gleichung, die Quantenbillard beschreibt, normale Schwingungen in Form stehender Wellen zu finden, die ein charakteristisches Muster von Knotenlinien und Gegenknoten aufweisen, das für jede Schwingung individuell ist und von der Form der Grenzen abhängt.

Beispiele für Profile der Schwingungsamplituden in stehenden Wellen im chaotischen Quantenbillard „ Pascals Schnecke “ und „ Stadion “.

Die Muster stehender Wellen in integrierbarem und chaotischem Quantenbillard sind qualitativ unterschiedlich: Integrierbares Billard zeigt symmetrische, geordnete Muster stehender Wellen, während in chaotischem Billard die Muster stehender Wellen sehr verwirrend sind und keine sichtbaren Muster zeigen (am Ende des Artikels wird gezeigt, dass einige interessant sind Muster existieren noch).

Die Schwingungsamplituden in den stehenden Wellen eines integrierbaren runden Billards (obere Reihe) und chaotischen Billards in Form einer Pascal-Schnecke (untere Reihe). Quelle

Die bizarren Bilder normaler Schwingungen im chaotischen Billard dienen manchmal als Gegenstand einer separaten Studie. Quelle

Ein qualitativer Unterschied zeigt sich auch in den Mustern der Knotenlinien: Bei integrierbaren Quantenbillard sehen wir geordnete Familien sich kreuzender Linien, und bei chaotischem Billard schneiden sich diese Linien in der Regel nicht .

Oben: Knotenlinien (schwarze Linien zwischen blauen und roten Bereichen) stehender Wellen aus integrierbarem - rundem und rechteckigem - Billard. Unten: die Knotenlinien einer der stehenden Wellen im chaotischen Billard - ein Viertel des Stadionbillards .

Überschneiden oder nicht überschneiden?

Warum kreuzen sich die Knotenlinien im chaotischen Billard nicht? 1976 bewies die Mathematikerin Karen Uhlenbeck einen Satz, nach dem sich die Knotenlinien stehender Wellen von Quantenbillard im Allgemeinen nicht schneiden sollten.

In vereinfachter Form kann dies wie folgt gezeigt werden: Angenommen, zwei Knotenlinien schneiden sich an einem Punkt ( x ₀ , y ₀ ). Dazu muss die Funktion f ( x, y ), die die Abhängigkeit der Amplitude der stehenden Welle von den Koordinaten bestimmt, gleichzeitig drei Bedingungen erfüllen:

1) Sie muss am Punkt ( x ₀ , y ₀ ) gleich Null sein, da dieser Punkt ein Knoten ist.
2) Wenn Sie sich vom Punkt ( x ₀ , y ₀ ) in Richtung der ersten Knotenlinie bewegen, sollte f ( x, y ) gleich Null bleiben.
3) Wenn Sie sich vom Punkt ( x ₀ , y ₀ ) in Richtung der zweiten Knotenlinie bewegen , sollte auch f ( x, y ) gleich Null bleiben.


Insgesamt haben wir drei Bedingungen (oder drei Gleichungen), die der Funktion von zwei Variablen f ( x, y ) auferlegt werden. Wie wir wissen, reicht eine Gleichung nicht aus, um die beiden Unbekannten x und y vollständig zu finden, zwei Gleichungen reichen dafür bereits aus, und drei Gleichungen sind zu viel. Das System der drei Gleichungen für zwei Unbekannte wird im Allgemeinen keine Lösungen haben, es sei denn, wir haben das Glück. Daher können die Schnittpunkte der Knotenlinien nur ausnahmsweise existieren .

Bei integrierbarem Billard treten solche Ausnahmen nur auf. Wie wir oben gesehen haben, sind ihre besonderen Eigenschaften - Vorhersagbarkeit der Bewegung, Abwesenheit von Chaos, regelmäßige Muster stehender Wellen - das Ergebnis ihrer hohen Symmetrie. Die gleiche Symmetrie gewährleistet die gleichzeitige Erfüllung von drei Bedingungen, die für Schnittpunkte von Knotenlinien erforderlich sind.

Schauen wir uns nun Beispiele von Hladni-Figuren genauer an, die für integrierbares und chaotisches Billard typisch sind. Die folgende Abbildung zeigt drei charakteristische Fälle . Links hat die Platte die Form eines Kreises, so dass das entsprechende Quantenbillard integrierbar ist und sich die Knotenlinien schneiden. In der Mitte ist die Platte rechteckig, was ebenfalls einem integrierbaren System entspricht. Eine runde Montage in der Mitte verletzt jedoch leicht die Symmetrie des Rechtecks, sodass sich die Knotenlinien nicht überall schneiden. Rechts ist ein Beispiel für ein rein chaotisches System dargestellt: eine Platte in Form eines Viertels des Sinai-Billards (in der oberen rechten Ecke befindet sich ein kreisförmiger Ausschnitt), deren Knotenlinien sich nicht mehr schneiden.



Je stärker die Form der Platte - unter Berücksichtigung ihrer Befestigung - von der Form eines integrierten Billard (z. B. eines Kreises oder Rechtecks) abweicht, desto weniger Schnittpunkte von Knotenlinien .

Es ist nicht so einfach, schöne Hladni-Figuren mit sich kreuzenden Linien auf einem runden Teller zu bekommen. Bei der Anregung von Vibrationen mit einer zentralen Halterung verhindert die Kreissymmetrie des gesamten Systems die Bildung radialer Knotenlinien, sodass nur ein langweiliger Satz von Kreisen angezeigt wird (diese Schwierigkeit kann durch Anregung von Vibrationen nicht von der Mitte, sondern vom Rand der Platte mit dem Bogen der Geige umgangen werden). Wenn die Platte außermittig fixiert ist, werden die Hladni-Figuren interessanter, aber aufgrund der Verletzung der Kreissymmetrie ist das System nicht mehr integrierbar.

Runde Platte, Mittelbefestigung.

Runde Platte, Montage von der Mitte verschoben.

Und hier gibt es verschiedene Optionen mit runden und unrunden Platten.

Schließlich mag ein aufmerksamer Leser bemerken: aber ich sehe, dass sich die Knotenlinien manchmal sogar auf „chaotischen“ Platten schneiden. Wie kommt es, dass ihr Schnittpunkt nach Uhlenbecks Theorem verboten ist?

Erstens können die Knotenlinien Schnittpunkte vermeiden, aber vorher kommen sie sich so nahe, dass es uns aufgrund der endlichen Breite des Sandwegs so erscheint, als gäbe es einen Schnittpunkt. Zweitens gibt es zwischen integrierbaren und chaotischen Systemen tatsächlich keine scharfe Grenze.

Knotenlinien - sie trennen schwarze und weiße Bereiche - in integrierbarem und chaotischem Quantenbillard (links und rechts) und im dazwischenliegenden pseudointegrierbaren Fall (in der Mitte). Im Zwischenfall gibt es mehrere Schnittpunkte der Knotenlinien, während es im chaotischen Fall überhaupt keine gibt. Quelle

In der klassischen Chaostheorie widmet sich die berühmte Kolmogorov-Arnold-Moser-Theorie diesem Thema. Sie sagt, dass wenn die Symmetrie des integrierbaren Systems leicht verletzt wird, es nicht sofort chaotisches Verhalten zeigt, sondern größtenteils seine Vorhersagbarkeit der Bewegung beibehält. Auf der Ebene der Quantentheorie des Chaos und der Hladni-Figuren manifestiert sich dies in der Tatsache, dass an einigen Stellen Schnittpunkte von Knotenlinien erhalten bleiben. Dies geschieht entweder an besonders symmetrischen Punkten des Billards oder weit entfernt von der Störquelle, die die Symmetrie des integrierbaren Systems verletzt.

Was sonst?

Was ist sonst noch interessant in der Quantentheorie des Chaos? Für den interessierten Leser werde ich drei zusätzliche Fragen erwähnen, die nicht mehr direkt mit den Figuren von Hladni zusammenhängen.

1) Ein wichtiges Phänomen, das von dieser Theorie untersucht wird, ist die Universalität chaotischer Systeme. Die überwiegende Mehrheit der Systeme, in denen normale Vibrationen auftreten können, ist chaotisch und alle - unabhängig von ihrer physischen Natur! - die gleichen Gesetze befolgen. Das Phänomen der Universalität, in dem völlig unterschiedliche Systeme durch dieselben Formeln beschrieben werden, ist selbst sehr schön und erinnert an die mathematische Einheit der physischen Welt.

Statistik der Abstände zwischen benachbarten Frequenzen normaler Schwingungen in chaotischen Systemen unterschiedlicher physikalischer Natur, die überall durch dieselbe universelle Wigner-Dyson-Formel beschrieben werden. Quelle

2) Die Muster normaler Schwingungen von chaotischem Billard haben ein interessantes Merkmal, das als "Quantennarben" bezeichnet wird . Wir haben gesehen, dass die Wege des Balls in chaotischem Billard normalerweise sehr verwirrend aussehen. Es gibt jedoch Ausnahmen - dies sind periodische Umlaufbahnen , ziemlich einfache und kurze geschlossene Flugbahnen, auf denen der Ball periodische Bewegungen ausführt. Quantennarben werden als scharfe Verdickung stehender Wellen entlang periodischer Bahnen bezeichnet.

Quantennarben im Billard "Stadion", die entlang der periodischen Umlaufbahnen verlaufen, die durch rote und grüne Linien dargestellt werden. Quelle

3) Bisher haben wir über zweidimensionale Systeme gesprochen. Wenn wir die Ausbreitung von Wellen im dreidimensionalen Raum betrachten, können hier auch Knotenlinien entstehen, entlang derer die Schwingungsamplitude Null ist. Dies ist besonders wichtig, wenn Sie die Bose-Kondensation und Superfluidität untersuchen, bei der sich Tausende von Atomen als einzelne " Wellen der Materie " bewegen. , , , .

« » -. .

^(*) , , , , , .

^(**) «» «» , : – , , . .

^(***) – . , , , .

^(****) , – . , . – .