Kann ein toroidaler Planet existieren?

Nach der Veröffentlichung meines Artikels über die Erde, wenn sie doppelt so groß wäre, hatten die Leser die Frage: „Was ist mit der torusförmigen Erde?“ Die Frage ist nicht die originellste, dieses Thema wurde bereits online diskutiert und seine Modellierung wurde durchgeführt. Aber ich mache gerne alles selbst, also habe ich versucht, meine eigene Analyse durchzuführen.

Kann ein toroidaler Planet existieren?

Die Stabilität eines toroidalen Planeten ist nicht offensichtlich. Aus praktischer Sicht können Planeten als flüssige Kugeln ohne Oberflächenspannung betrachtet werden - die Stärke eines Steins kann nicht mit dem Gewicht eines Planeten verglichen werden. Sie besitzen äquipotentielle Gravitationsflächen unter Berücksichtigung des Zentrifugalpotentials. Wenn dies nicht so wäre, gäbe es Orte auf ihnen, die ihre Energie reduzieren könnten, indem sie in Richtung eines niedrigeren Potentials fließen. Eine weitere offensichtliche Tatsache ist das Vorhandensein der Obergrenze der Rotationsgeschwindigkeit, nach der der Planet auseinander fällt: Die Zentrifugalkraft am Äquator übersteigt die Schwerkraft und das Material fliegt in den Weltraum.

Die Gleichgewichtsformen der rotierenden ellipsoiden Planeten, die durch die Kraft ihrer eigenen Schwerkraft gehalten werden, wurden umfassend analysiert . Alles begann mit Newton, dann wurden frühe heldenhafte Expeditionen durchgeführt, um die Form der Erde zu bestimmen. Maclaurin setzte seine Arbeit fort. Jacobi entdeckte, dass Ellipsoide mit ungleichen Achsen bei hohen Rotationsgeschwindigkeiten stabiler sind als abgeflachte Macloren-Ellipsoide. Subramanyan Chandrasekar leitete interessante Entwicklungen in diesem Bereich. Seitdem sind jedoch Computer erschienen, und daher wurden analytische und numerische Berechnungen komplexerer oder relativistischer Fälle durchgeführt.

Auf die gleiche Weise wurden die Gleichgewichtsformen rotierender Toroide analysiert - dies wurde von Poincare , Sophia Kovalevskaya und Frank Dyson ( Dyson 1893 , Dyson 1893b ) durchgeführt. Zumindest theoretisch ist es möglich, einen ellipsoiden Planeten in einen Ringzustand abzuwickeln , obwohl es viele Möglichkeiten für das Auftreten von Schwingungen gibt, die das System destabilisieren, wonach ein Sprung in den Ringzustand erfolgt.

Der Ring kann insbesondere aufgrund einer "Knoten" -Instabilität instabil sein - in bestimmten Meridianen kann sich eine zunehmende Menge an Masse ansammeln, wodurch es zu einer Lücke in mehreren getrennten Massen kommt. Dyson analysierte diesen Fall und stellte fest, dass es wichtig ist, wenn R (der Abstand von der Mitte des Torus zur Mitte des Rohrs) r (den Radius des Rohrs) mehr als dreimal überschreitet - das heißt, dünne Reifen erweisen sich als instabil. Es gibt auch eine niedrigere Drehzahl, bei der der Ring instabil wird und Gezeitenkräfte ihn zu einem Ellipsoid komprimieren . Die Gesamtmasse und der Drehimpuls müssen also von Anfang an richtig eingestellt sein.

Anscheinend verbieten die Gesetze der Physik das Erscheinen von Ringplaneten nicht. Nur die Wahrscheinlichkeit ihres Auftretens ist äußerst gering, und ein solcher Planet ist auf der geologischen Zeitskala aufgrund äußerer Störungen wahrscheinlich instabil. Wenn wir also annehmen, dass es bereits existiert, möglicherweise aufgrund der Handlungen einer fortgeschrittenen Zivilisation, deren Ästhetik stärker ist als der Geist - welche Eigenschaften werden sie haben?

Richtungen

Wir werden zwei Kreise parallel zur Rotationsebene der Äquatoren (extern und intern) nennen. Für den Fall, dass es für das diskutierte Thema keinen grundsätzlichen Unterschied zwischen ihnen gibt, werde ich sie einfach den Äquator nennen. Die Pole sind die Kreise, die am weitesten von der Äquatorialebene entfernt sind.

Die Richtung zur Mitte gibt die Richtung zur Rotationsachse zum Rand an - von der Rotationsachse. Zur Ebene - zur Äquatorialebene. Norden - in Richtung des nächsten Teils des Nordpolkreises, Süden - in Richtung des nächsten Teils des Südpolkreises.

Toroid Schwerkraft

Wie funktioniert die Schwerkraft auf einem Ringplaneten?

Bei sehr großem R wird der Ringplanet im wesentlichen zylindrisch. In diesem Fall nimmt die Schwerkraft mit 1 / r ab, wobei r der Abstand von der Achse ist. Die Wirkung auf einen Abschnitt ist proportional zur Gesamtmasse (proportional zu R) und zur Schwerkraft (proportional zu 1 / R), so dass die Gesamtkraft mit zunehmendem R konstant bleibt. Sie gleicht eine bestimmte Drehung aus. Oberflächengravitation 2G rho / r, wobei rho die Masse pro Längeneinheit ist. Solange die Oberflächengravitation groß genug ist (mit kleinem r), überwindet diese Kraft die Zentrifugalbeschleunigung und fliegt nicht weg. Bei einem Torus mit kleinem Radius ist jedoch alles viel komplizierter.

Ich entschied mich für die Monte-Carlo-Methode, um die Gleichgewichtsform zu bewerten. Beginnend mit der Gesamtmasse des Planeten und dem Drehimpuls verteilte ich viele massive, unendlich dünne Ringe (das Potenzial, das ich aus dieser Übung genommen habe, ist gut, dass in der klassischen Physik das elektrische und das Gravitationspotential gleich sind). Ich berechnete ihr Gesamtpotential und fügte Zentrifugal hinzu. Dies ermöglicht es uns, Äquipotentialflächen zu approximieren und das Potential näher am Zentrum des Torus mit einer zunehmenden Anzahl von Ringen zu „füllen“, bis ihre Masse der Masse des Planeten entspricht. Ich habe die Winkelgeschwindigkeit basierend auf der neuen Massenverteilung neu berechnet. Dann wiederholte er den Vorgang, bis entweder der Planet zerstreut oder zu einer Kugel zusammengedrückt war oder viele Iterationen vergangen waren. Dies ist nicht die eleganteste Methode (in der Literatur wird die Zerlegung in eine Reihe von torusförmigen Harmonischen verwendet), aber es hat mir gereicht.

Das Hauptergebnis ist, dass ein toroidaler Planet realistisch genug Masse und Drehimpuls zulässt. Der Abschnitt ist weder rund noch elliptisch, sondern ähnelt einem Ei mit einer etwas schärferen inneren Krümmung als die Außenseite.

Warum flacht der Planet nicht zu einer Scheibe ab? Die Rotation versucht, den Planeten zu glätten, muss jedoch gegen die lokale Schwerkraft arbeiten, die versucht, ihn zu einer Kugel (oder einem Zylinder) zusammenzudrücken.

Obwohl sich in meiner Simulation solche Planeten als stabil herausstellten, war der Bereich akzeptabler Werte nicht groß: Die meisten Kombinationen von Masse und Drehimpuls waren instabil. Ich habe das komplexe Problem der Knoteninstabilität nicht analysiert.

Ich werde hier einen molligen Toroid mit einer Masse betrachten, die der Masse der Erde entspricht, und ein kleines zentrales Loch ("Donut") sowie einen breiteren, reifenartigen Toroid mit einer Masse von 6 Erde, aber näher an der Erdgravitation ("Hoop").

Donut

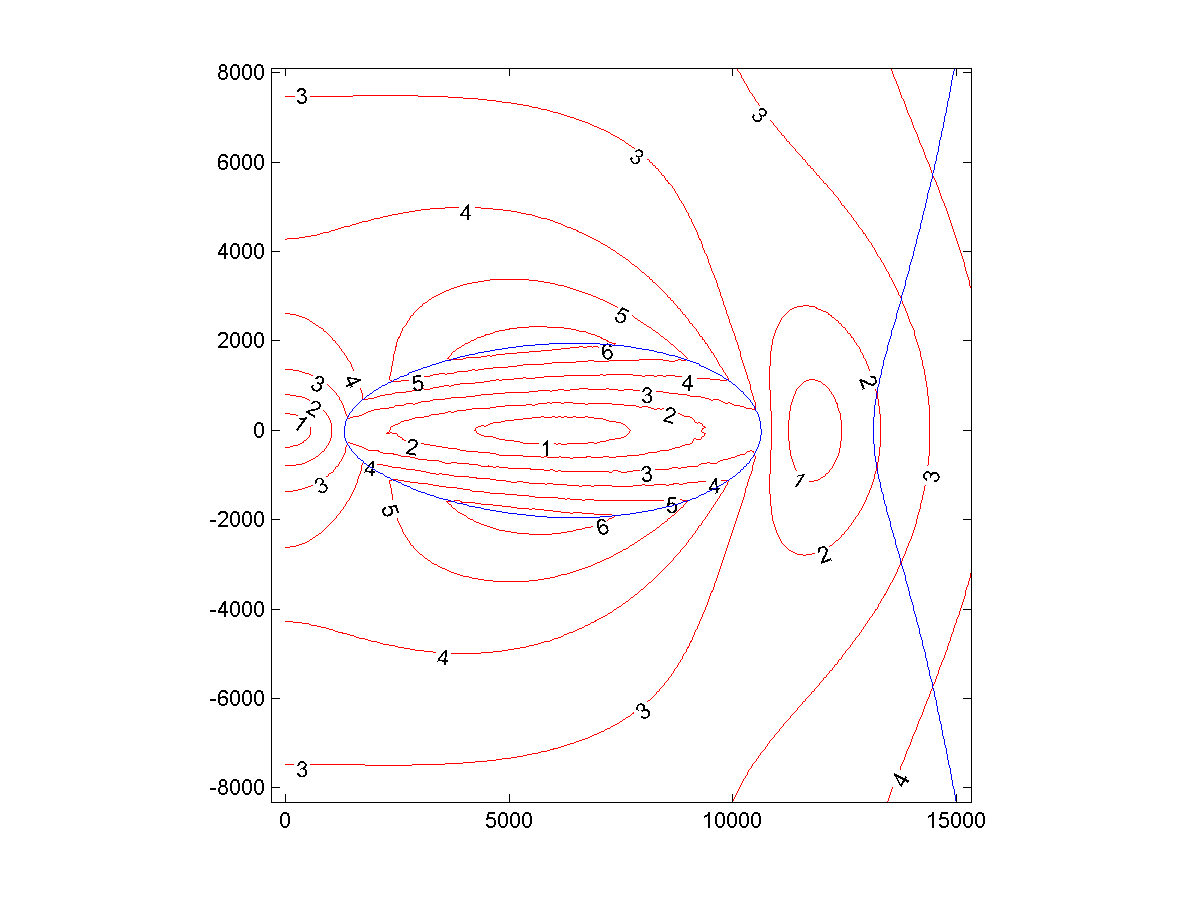Abb. 1: lokale Gravitationsbeschleunigung (m / s ² ) um den Donut, die von einem Objekt erlebt wird, das sich mit ihm dreht

Der innere Äquator des Donuts ist 1305 km vom Zentrum entfernt und der äußere - 10663 km. Der Durchmesser des Äquators beträgt 9328 km.

Der Planet erstreckt sich über eine Entfernung von 1953 von der Äquatorialebene und der Durchmesser von Nord nach Süd beträgt 3906 km. Das Durchmesserverhältnis beträgt 2,4.

Der Umfang von Nord nach Süd beträgt 21587 km (0,54 irdisch) und von West nach Ost 66809 km (1,7 irdisch). Die Gesamtfläche beträgt 8,2 x 10 ⁸ km ² (1,6 Land). Das Gesamtvolumen = 1,1 x 10 ¹² km ³ unterscheidet sich von der Erde um nicht mehr als 1% (schließlich wurde der Donut als Planet der Erdmasse ausgewählt). Das Verhältnis von Volumen zu Fläche - 1300, 61% der Erde - pro Flächeneinheit mehr.

Der Tag dauert 2,84 Stunden.

Hoop

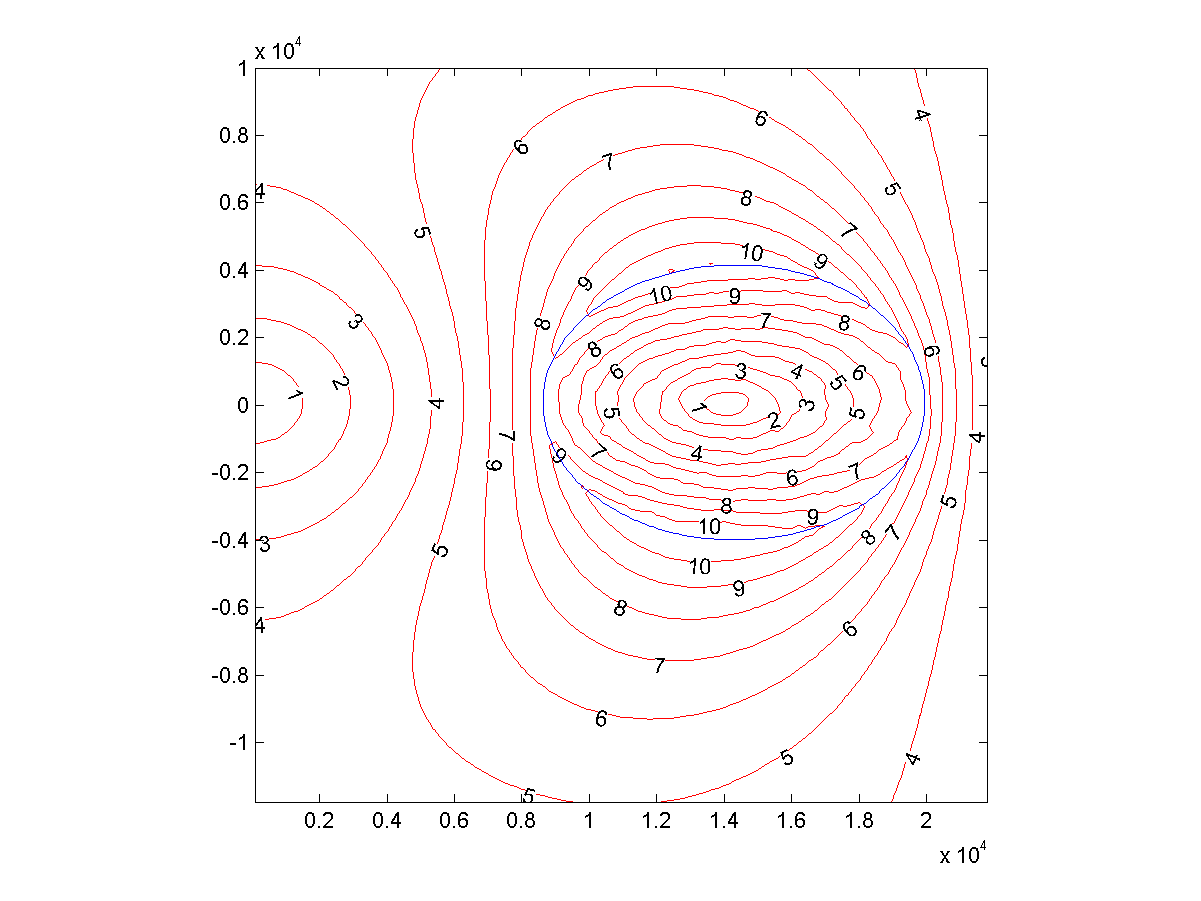
Abb. 2: lokale Gravitationsbeschleunigung (m / s ² ) um den Reifen herum, die von einem Objekt erlebt wird, das sich mit ihm dreht

Der innere Äquator von Hoop ist 8633 km vom Zentrum entfernt und der äußere - 19937 km. Der Durchmesser des Äquators beträgt 11.304 km.

Der Planet erstreckt sich von der Äquatorialebene über 4070 km, der Durchmesser von Nord nach Süd - 8141 km. Das Seitenverhältnis des Abschnitts beträgt wie bei alten Monitoren ungefähr 4: 3. Der Radius des Kreises des Schwerpunkts beträgt 14294 km.

Der Umfang von Nord nach Süd beträgt 30794 km (0,77 irdisch) und von West nach Ost - 125270 (3,1 irdisch). Die Gesamtfläche von 2,5 x 10 ⁹ km ² , 4,9-mal größer als die Erde, und das Gesamtvolumen von 6,5 x 10 ¹² km ³ , 6-mal größer als die Erde. Das Verhältnis von Volumen zu Fläche = 150, 70% der Erde.

Der Tag dauert 3,53 Stunden.

Umgebung

Wie sieht das Leben auf einer torusförmigen Erde aus?

Schwerkraft

Die Oberflächengravitation ist ortsabhängig. Es ist das schwächste entlang des inneren und äußeren Äquators und das stärkste - in der Nähe der Pole, leicht zur Mitte hin. Dies ist einer der Hauptunterschiede.

Donut

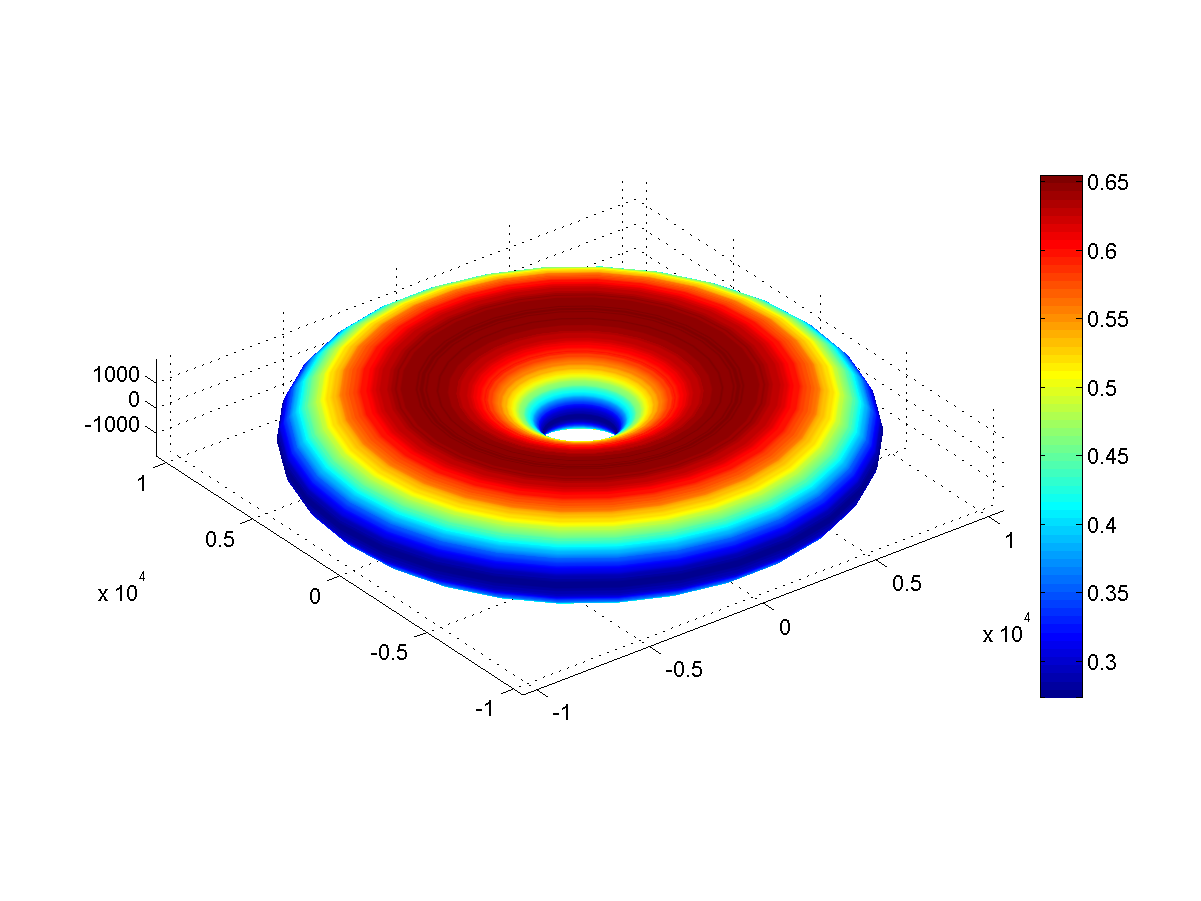Abb. 3: Donutoberflächengravitation (m / s ² )

Am Donut beträgt die Schwerkraft entlang der Äquatoren nur 0,3 G und entlang der Pole 0,65 G. Die Fluchtgeschwindigkeit unterscheidet sich nicht zu stark von der Erde und beträgt 11,4 km / s.

Die geosynchrone Umlaufbahn um den Donut liegt sehr nahe am äußeren Äquator, weniger als 2000 km. Ein Satellit, der daran entlang fliegt, bleibt über einem Ort, kann aber im Gegensatz zur Erde nicht die gesamte Hemisphäre mit Zahnrädern bedecken, sondern nur einen kleinen Bereich.

Andererseits beträgt die Umfangsgeschwindigkeit am Äquator 6,5 km / s, und Starts sind einfacher durchzuführen. Eine nach Osten abgefeuerte Rakete benötigt eine Geschwindigkeit von nur 4,9 km / s, um zu entkommen.

In der Mitte des Lochs befindet sich ein instabiler Lagrange-Punkt. Der Satellit dort wird von der Äquatorialebene angezogen, aber jede Abweichung davon nimmt zu.

Hoop

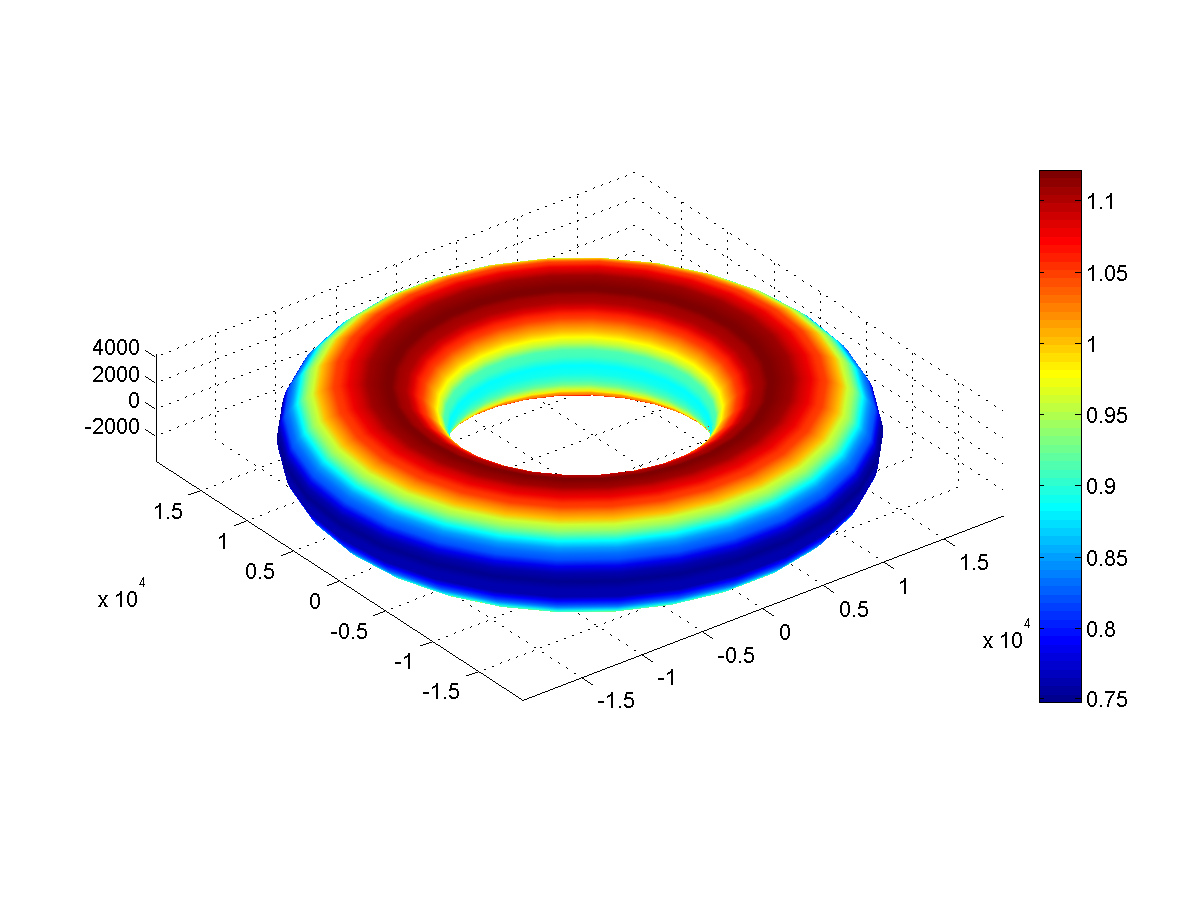Abb. 4: Oberflächengravitation (m / s ² ) Reifen

Bei Hoop beträgt die Schwerkraft entlang der Pole 1,1 G und entlang des äußeren Äquators nur 0,75 G. Am inneren Äquator ist sie mit etwa 0,81 G etwas größer.

Die außer Kontrolle geratene Geschwindigkeit beträgt 19 km / s (denken Sie daran, dass der Planet sechsmal mehr wiegt als die Erde). Am äußeren Äquator beträgt die Geschwindigkeit 9,9 km / s - eine im Osten abgefeuerte Rakete muss eine Geschwindigkeit von 10 km / s erreichen.

Ich stelle noch einmal fest, dass eine niedrige Schwerkraft am Äquator und eine hohe Schwerkraft an den Polen nicht bedeutet, dass Dinge zu den Polen rollen oder kriechen: Wie bereits erwähnt, ist die Oberfläche äquipotential, sodass die Schwerkraft zusammen mit der Zentrifugalkorrektur immer senkrecht dazu steht.

Luftmassen, die zu den Polen strömen, werden abgeflacht. Die Schwerkraftdifferenz erzeugt eine horizontale Druckdifferenz, die zusammen mit der Temperaturdifferenz nicht triviale Strömungen erzeugt.

Das Licht

Nächte und Tage auf solchen Welten werden sehr kurz sein. Die Umgebung hat während der täglichen Zyklen keine Zeit zum Abkühlen oder Aufwärmen. Was zählt, ist der Unterschied in der Lichtmenge, die während längerer Zeiträume, dh Jahreszeiten, empfangen wird. Wenn sich diese Welten in einer erdähnlichen Umlaufbahn um einen sonnenähnlichen Stern bewegen, ist das wichtig.

Wenn die Umlaufbahn kleiner ist, werden diese Planeten durch Gezeitenkräfte bald instabil. Da die Helligkeit eines Sterns ungefähr mit dem vierten Grad seiner Masse zunimmt und der Radius der lebenden Zone als Quadratwurzel der Helligkeit wächst, beträgt die Skala der Gezeitenkräfte in der Wohnzone M / (√ (M ⁴ )) ³ = 1 / M ⁵ . Das heißt, die Gezeiteneffekte heller Sterne sind viel geringer - vielleicht ist es für Donut und Hoop besser, sich um einen blau-weißen Stern der Klasse F zu drehen und nicht um einen Stern der Klasse G wie unsere Sonne, nur für den Fall.

Der äußere Teil des Ringplaneten unterscheidet sich nicht zu sehr von der Oberfläche eines normalen Ellipsoids. Der Tag kommt, an dem die Sonne über dem östlichen Horizont aufgeht und der Sonnenuntergang über dem westlichen Horizont stattfindet. Die Sonne bewegt sich in einem großen Kreis und bewegt sich im Laufe des Jahres langsam von Nord nach Süd und zurück, wodurch die Verfügbarkeit von Jahreszeiten sichergestellt wird. Im Inneren des Planeten ist jedoch alles anders. Andere Teile des Planeten können die Sonne verdecken - in erster Näherung ist weniger Energie zu erwarten.

Wir können drei verschiedene Fälle betrachten: Neigung der Nullachse, 23 Grad (wie die Erde) und 45 Grad.

Keine Neigung

Bei einer Neigung von Null wird die Innenseite der Sonne nicht sehen: Sie wird immer hinter dem Horizont oder hinter dem Weltbogen versteckt sein. An den Polen bewegt sich die Sonne am Horizont entlang, und etwas näher am Zentrum wird es immer Dämmerung geben. Die Temperaturunterschiede werden groß sein, der innere Teil des Planeten wird subarktischen Temperaturen ausgesetzt sein - dies unterscheidet sich nicht wesentlich von der Welt mit synchroner Rotation , und im Prinzip sollte Wasser (und möglicherweise Kohlendioxid) immer an diesen Orten kondensiert werden. Infolgedessen sollte es am äußeren Äquator trockene (möglicherweise nicht zu heiße) Stellen geben, möglicherweise bewohnte Dämmerungsgebiete in der Nähe der Polargebiete und ein eisiges Inneres.

23 Grad Neigung

Abb. 5: Donut-Jahreszeiten im Frühling, Sommer, Herbst und Winter

Bei einer Neigung von 23 Grad, die mit der Erde zusammenfällt, fallen Frühling und Herbst mit einer Neigung von Null zusammen - hell entlang des Äquators und dunkel innen in der Nähe des Lochs. Im Sommer und Winter kann die Sonne hinter den Rand auf der gegenüberliegenden Seite des Lochs eindringen. Es wird auch große Gebiete mit der Sonne um Mitternacht oder mit der ewigen Nacht im Sommer oder Winter geben. Auf der Erde sind die Polarregionen klein, aber hier sind es lange durchgehende Kreise.

Frühlingssonnenaufgänge und Herbstdämmerung im Inneren sollten erstaunlich tiefe Farben ergeben, da die Sonne durch die Atmosphäre auf der anderen Seite des Planeten aufgehen wird (zuvor aufgegangen oder untergegangen, wenn ich so sagen darf). All dies führt zusammen mit lokalen atmosphärischen optischen Effekten zu sehr tiefen Rottönen und Farbverläufen. Unmittelbar vor oder nach Sonnenuntergang oder Morgengrauen sind Teile der Sonnenkorona sichtbar.

Dieses Spektakel wäre beeindruckender gewesen, wenn es nicht so kurz gewesen wäre. Auf der Erde geht die Sonne etwa 15 ° pro Stunde. Im schnellsten Fall passiert die Sonne in 2,1 Minuten einen ihrer Durchmesser. Auf dem Donut geht die Sonne 127 ° pro Stunde und auf Obruch 102 °. Sonnenaufgang und Sonnenuntergang dauern 15 bzw. 19 Sekunden. Der Neigungswinkel und die atmosphärischen Verzögerungen verlängern die Sicht geringfügig, aber für einen Bewohner der Erde ist sie zu kurz.

Wenn Sie auf der Innenseite der Oberfläche stehen und nach oben schauen, nimmt die andere Seite auf Obruch 20 Grad des Himmels und auf dem Donut 30 Grad ein - ein riesiger Bogen durch den gesamten Himmel.

Warum ist Donut nicht viel breiter? Es ist sehr flach, so dass es am Himmel kürzer aussieht. Dies bedeutet übrigens, dass die roten Farben viel tiefer sind als bei Obruch, wenn das Sonnenlicht während der Morgendämmerung oder des Sonnenuntergangs durch die Atmosphäre der anderen Seite gebrochen wird.

Im beleuchteten gegenüberliegenden Teil des Torus wird alles wie Mondlicht beleuchtet. Die Oberfläche wird jedoch größer, sodass die Nächte viel heller werden. Auf Obruch ist das Licht 16.000 Mal stärker als die Erde (8.000 Lux), wenn der gesamte gegenüberliegende Teil beleuchtet ist (nehmen wir die Albedo gleich der Erde), und die Nacht wird wie ein bewölkter Tag sein. Auf dem Donut erreicht die Beleuchtung ein schwaches Tageslicht (12.000 Lux). Dies ist jedoch die Situation der vollständig beleuchteten gegenüberliegenden Seite - während der Tagundnachtgleiche ist nur ein dünner Streifen sichtbar.


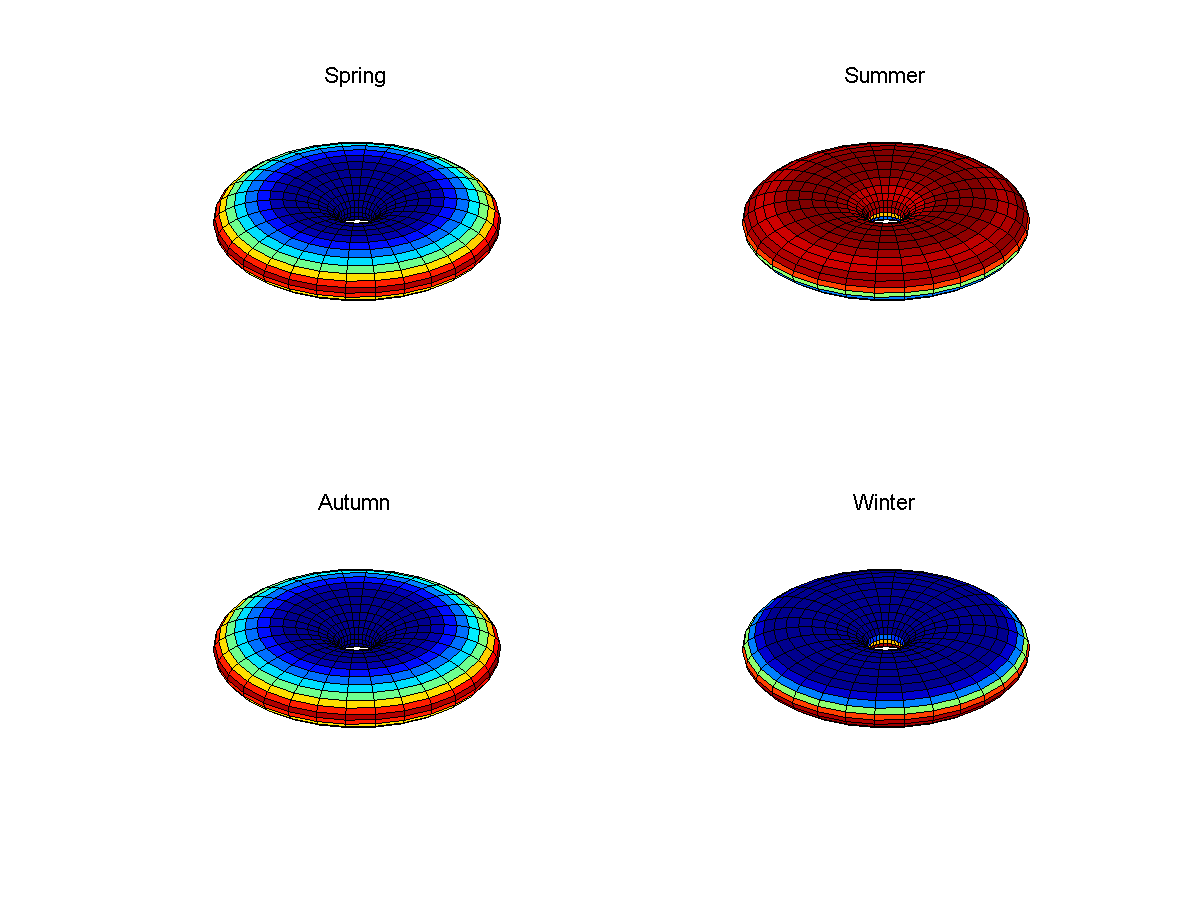Abb. 6: durchschnittliche tägliche Beleuchtung des Donuts im Frühling, Sommer, Herbst und Winter für den Fall mit einer Neigung von 23 Grad

Im Fall des Donuts bedeutet eine ziemlich flache Oberfläche, dass die nördliche oder südliche Hemisphäre (eineinhalb) viel Sonnenlicht erhält. Die totale Erwärmung des Planeten wird in diesen Jahreszeiten größer sein als im Frühling und Herbst, im Gegensatz zur Erde, wo sie konstant ist, da die Fläche, die Licht empfängt, konstant bleibt. Aufgrund der Winkel zwischen Oberfläche und Sonnenlicht werden auch nichttriviale Effekte beobachtet, und gemäßigte Zonen erhalten etwas weniger Energie als die Polarregionen und Tropen.

In den äußeren Tropen wird es ungefähr den gleichen Zufluss von Sonnenenergie geben. In Richtung der Pole ist die Saisonalität stärker zu spüren: Die Tropen erhalten im Sommer zu jeder Zeit mehr Energie als der Äquator. Die Winter werden genauso dunkel sein. An den Polen und dahinter, innen, an Orten mit maximaler Schwerkraft, ist die Sonne sechs Monate lang sichtbar, und dann gibt es eine polare Nacht. Hier wird sich das Klima dramatisch ändern - in den äußeren Tropen wird es mindestens 1,5 Stunden lang Nächte geben, und hier werden sie 6 Monate dauern. Näher am inneren Äquator neben dem Loch sind Tag und Nacht im Winter gleich (und das von der anderen Seite reflektierte Licht wird ebenfalls hinzugefügt), sodass die Temperatur etwas höher ist.


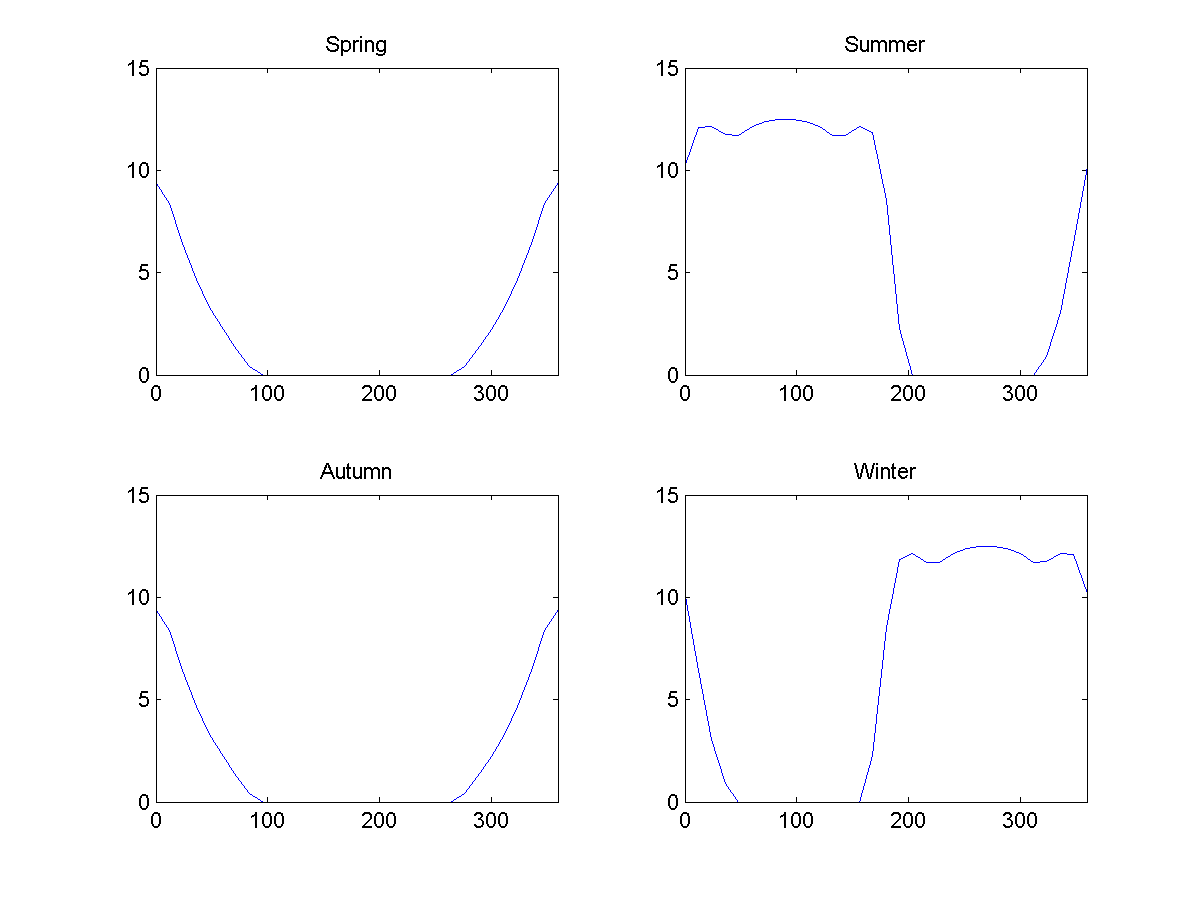Abb. 7: durchschnittliche Beleuchtung während verschiedener Jahreszeiten auf dem Donut als Funktion des Breitengrads bei 23 Grad. 0 steht für den äußeren Äquator, 90 steht für den Nordpol, 180 steht für den inneren Äquator, 270 steht für den Südpol.

Ein großer Unterschied in der Energiemenge, die auf der sonnigen Sommerseite des Lochs und auf der dunklen Winterseite des Lochs empfangen wird, führt zu Unwettern - aber aufgrund anderer Kuriositäten dieser Welten wird es schwieriger sein, den Energiedifferenz auszugleichen als auf der Erde.

Im Durchschnitt erhält der äquatoriale Außenteil 2,5-mal mehr Energie als die polaren Teile, und der Innenteil erhält viermal weniger Energie als die umgebenden Bereiche.


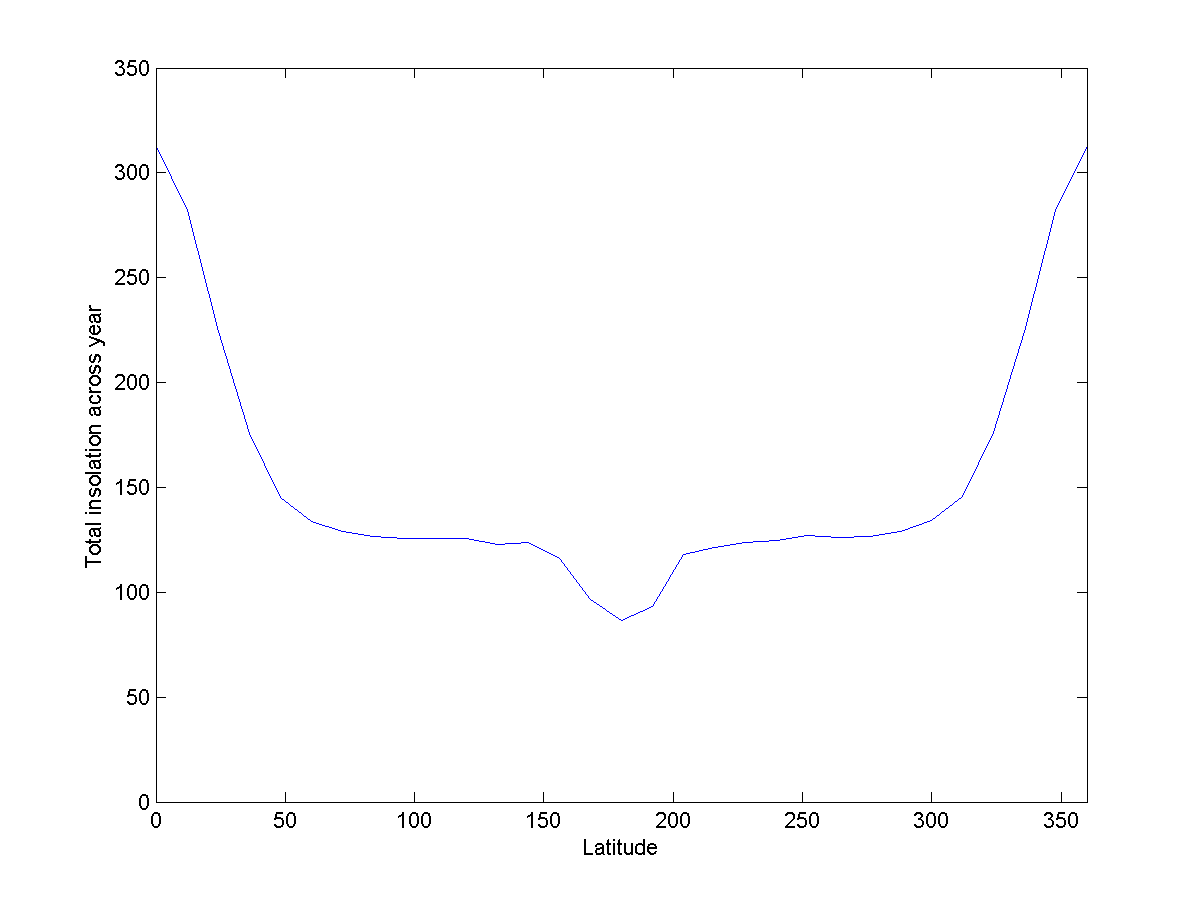Abb. 8: Energie in verschiedenen Breiten des Donuts

Der Reifen wirft weniger Schatten auf sich. Noch wichtiger ist, dass es nicht so flach ist wie der Donut.


Abb. 9: durchschnittliche Beleuchtung während des Tages auf Obruch, 23 Grad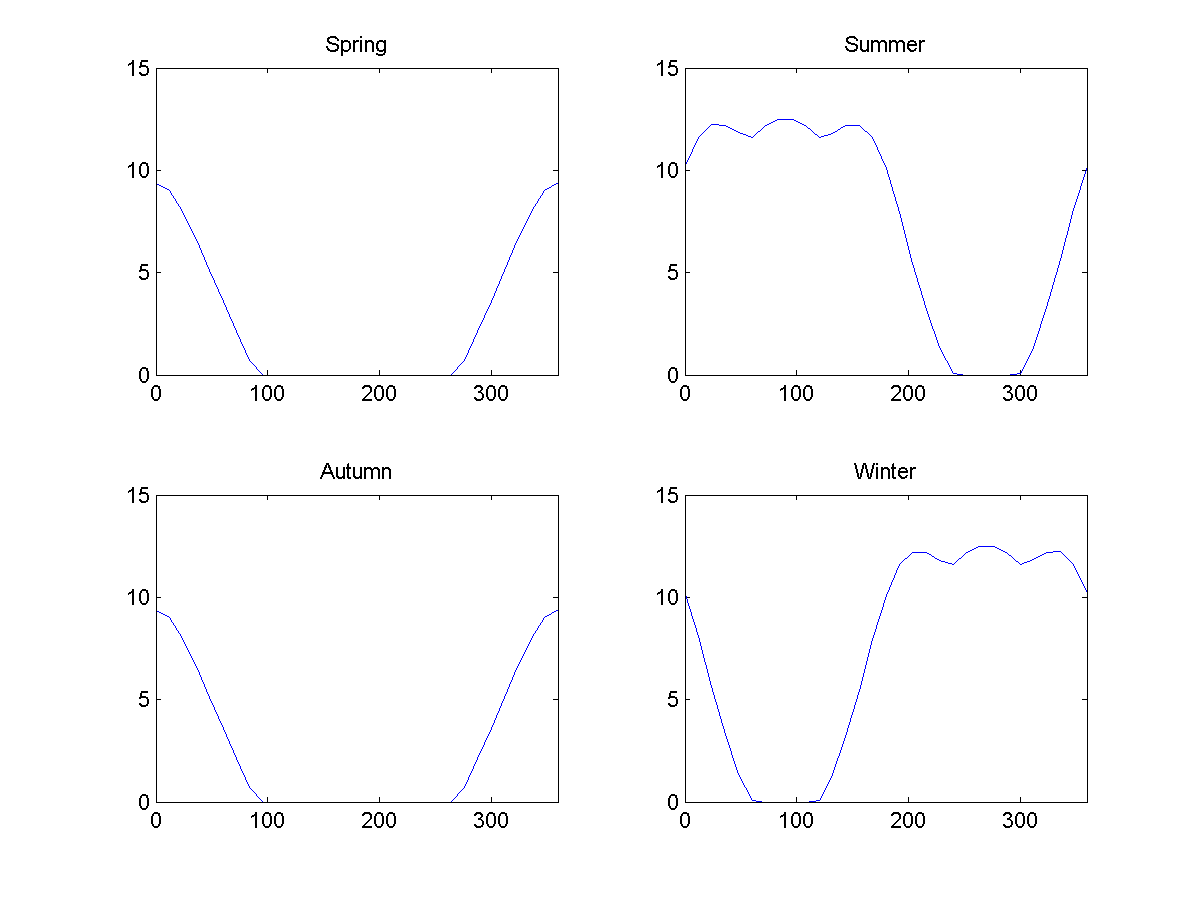


Abb. 10: durchschnittliche Beleuchtung während verschiedener Jahreszeiten auf Obruch als Funktion des Breitengrads bei 23 Grad. 0 steht für den äußeren Äquator, 90 steht für den Nordpol, 180 steht für den inneren Äquator, 270 steht für den Südpol.

Auf den ersten Blick sehen die Jahreszeiten wie erwartet aus. Im Frühling und Herbst werden die inneren Teile im Schatten versteckt, im Sommer und Winter wird eine Polarregion stärker beleuchtet und die andere ist schwächer, und die inneren Teile werden beleuchtet. Dies wird dazu führen, dass im inneren Teil des Planeten ein saisonaler Zyklus auftritt, der doppelt so schnell verläuft wie im äußeren (dies wird auch beim Donut der Fall sein): Das Wetter wird im Juli und Januar warm sein.


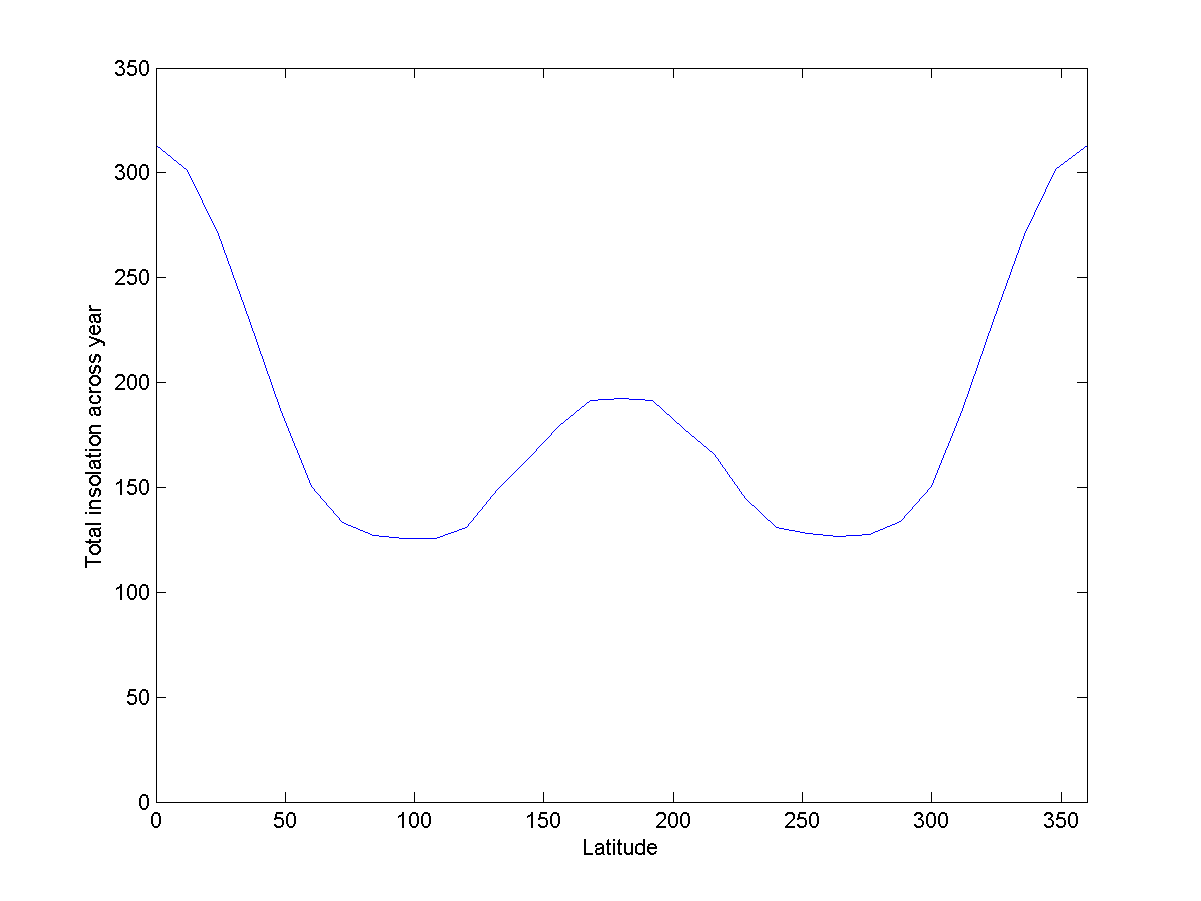Abb. 11: Energie, die im Laufe des Jahres in verschiedenen Breiten des Reifens aufgenommen wurde

Im Vergleich zu Donut ist dies nicht intuitiv - der interne Äquator erhält im Laufe des Jahres mehr Licht als die Polarregionen. Es ist zu erwarten, dass das Klima der Erde ähnelt - die Polarregionen sind kälter, die Äquatorregionen wärmer. 60%.

45

, – , !

, , 90 – , . , . , . – . , .


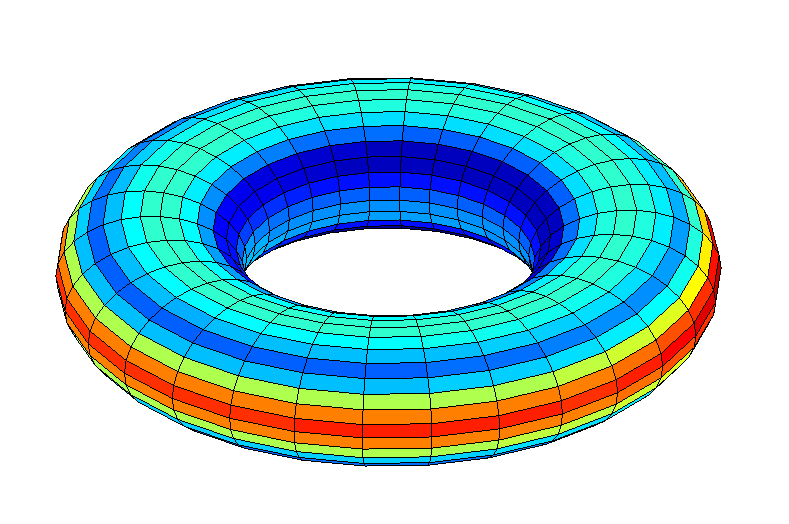Abb. 12: , 45

, 10% . .

, . .

, ( 1300 , 1500 , – 2124 ). , , . - . 6 , , 5 .

. , r R 2 π r , r/R. , , 43% . – 12% ! , , , , , . .

. , 1,5 ( 12 ), 3 (24 ). , .

. , , . - , .

, , , . , .

, , , . , «» , , : , , . : , , .

8 , . , , . , , , , . , – .

, (Intertropical Convergence Zone, ITCZ) , , , (), , , ( ). , , ITCZ , . , 30 ( , , ).

, , . : , , , .

, , . 1,5-3 , , .

, . – . ( ). , .

, , 6 , 5 , 20% - ( 20%). , , .

: , . ; , , . , . , , . , , .

: , . 150% . (133% , 90% ). .

, . , , . , , (, , ). , , – .

Werden diese Welten den Mond halten können?

Der Mond, der in einer kreisförmigen Umlaufbahn in der Nähe des Toroids in der Ebene des Äquators umkreist, spürt keine Unterschiede zu einem runden Planeten. Beim Erwerb von Exzentrizität werden die Dinge jedoch kompliziert. Ein potentielles Feld bei Annäherung an einen Planeten fällt langsamer als 1 / r, wie bei normalen Planeten: Die Kepler-Ellipse ist nicht mehr als Lösung geeignet. Mit der Neigung der Umlaufbahn wird das System noch komplexer - jetzt spürt der Mond die Flachheit des Planeten.

In gewisser Weise stehen Satellitenentwickler bereits vor einem ähnlichen Problem: Die Erde ist an den Polen so abgeflacht, dass sie sich bemerkbar macht. Dieses Problem wurde in den frühen Stadien der Raumfahrt gelöst (Wikipedia, (Tremaine & Yavetz 2013) oder (Nielsen, Goodwin & Mersman 1958).

Tatsächlich unterliegt eine elliptische Umlaufbahn einer Präzession - sie ändert allmählich die Richtung, und im Fall der Erde hängt dies von der Neigung der Umlaufbahn ab. Exzentrizität kann auch schwimmen. In jedem Fall sind diese Effekte bei einem Toroid stärker ausgeprägt. Sie werden so stark sein, dass Standardberechnungsmethoden nicht mehr funktionieren und wir Computersimulationen durchführen müssen.

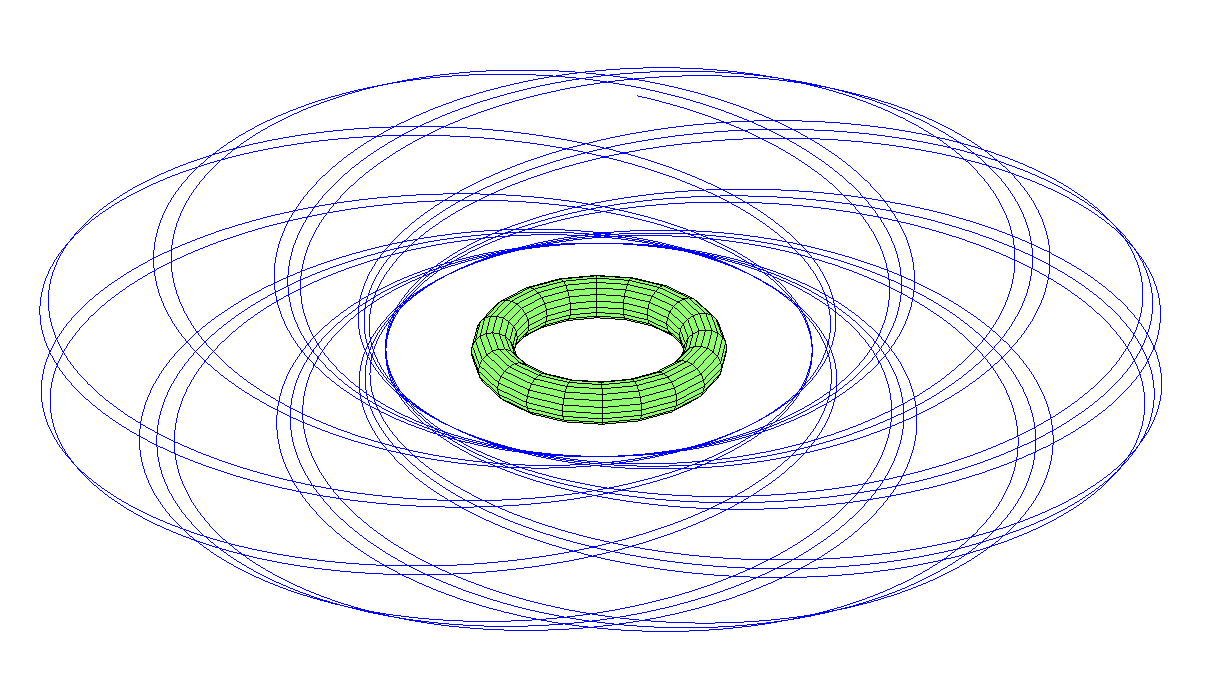
Ich bin sicher, dass sich die Monde in ausreichend entfernten Kreisbahnen recht stabil verhalten werden. Höchstwahrscheinlich unterliegen sie einer Präzession, sodass ihre Umlaufbahn eher einer Fassung als einer Ellipse ähnelt, aber sie fliegen nicht von Spulen ab. Wenn die Umlaufbahn des Mondes näher ist, wird natürlich alles anders sein.

In der Simulation (ich habe keinen vollen Torus verwendet, sondern einen Ring mit 30 Massen) eröffneten sich mir mehrere Möglichkeiten. Die äquatoriale elliptische Umlaufbahn sieht ordentlich und stabil aus, aber die Präzession verwandelt sie in einen Sockel.



Die zirkumpolare Umlaufbahn bewegt sich noch mehr, nicht nur der Auslass erscheint, sondern auch die Präzession der Ebene. Der Mond am Himmel kann in jeder Konstellation erscheinen.



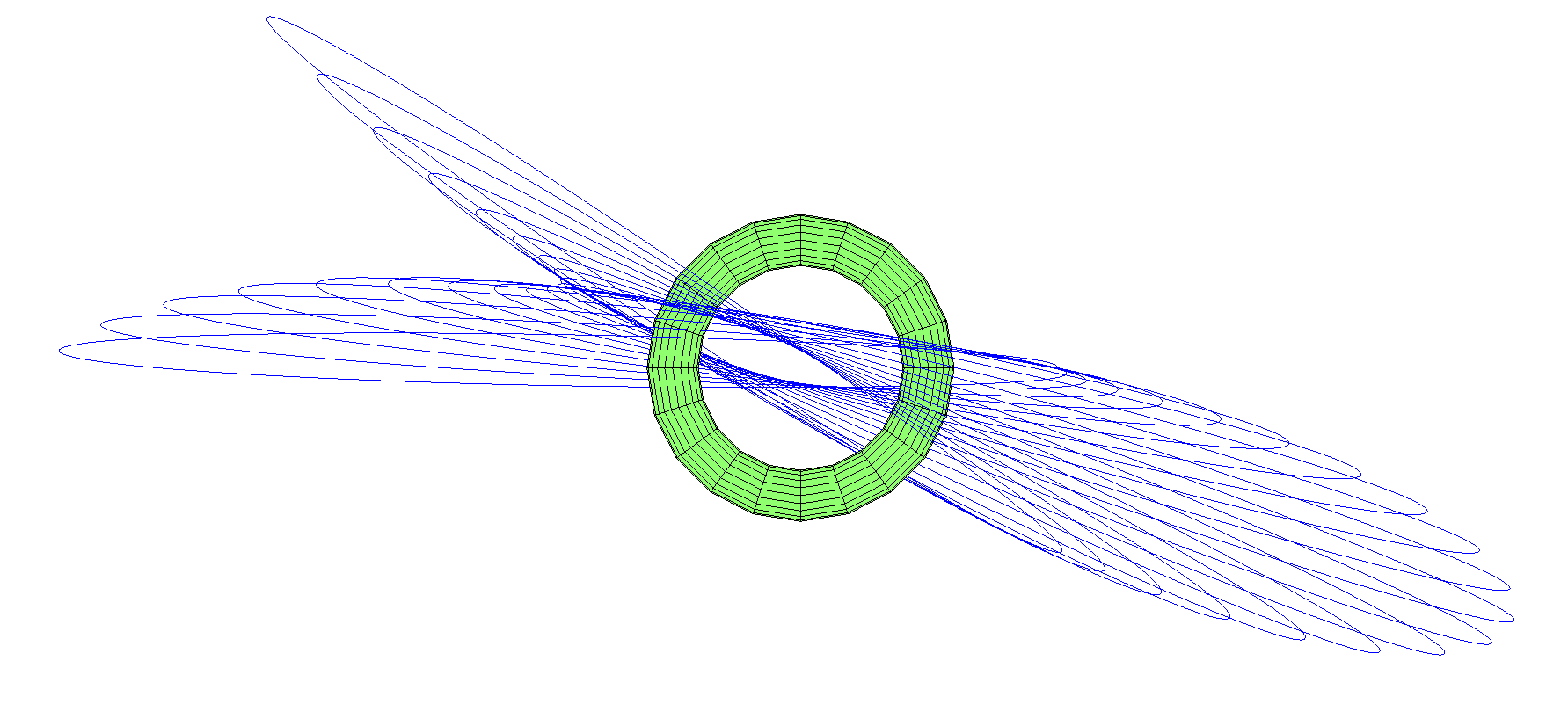
Was ist mit den Umlaufbahnen, die durch das Loch verlaufen? Wie ich bereits erwähnt habe, ist das geometrische Zentrum ein instabiler Lagrange-Punkt. Wenn Sie den Mond dort platzieren, wird ihn jeder Schlag dort rauswerfen. Es gibt jedoch stabil aussehende Umlaufbahnen durch das Zentrum (genauer gesagt, bei jedem Aufprall verwandeln sie sich in eine andere Umlaufbahn mit ähnlicher Form). Die einfachste Option ist der Mond, der wie ein Pendel durch ein Loch hin und her baumelt:



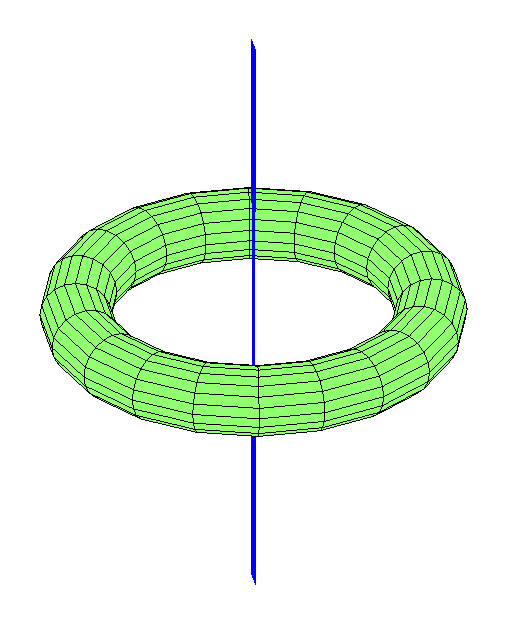
Sie können sich vorstellen, dass der Mond in einer bestimmten Länge fliegt:



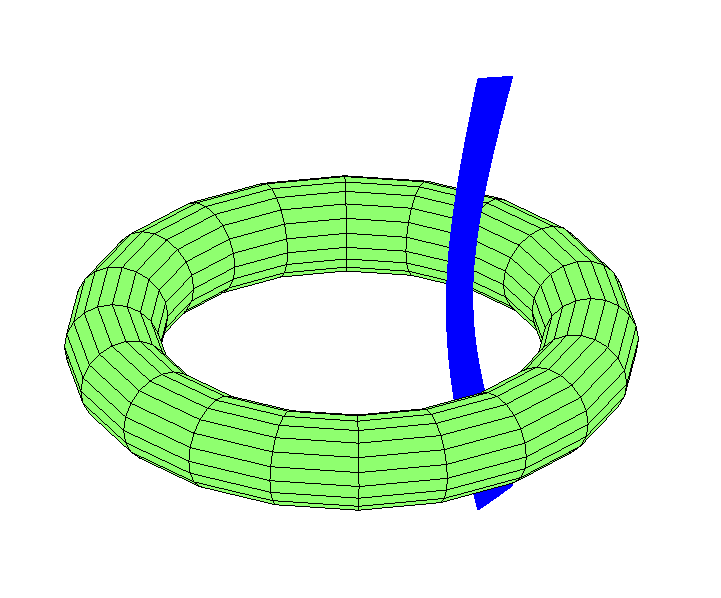
Mit der Erfassung der Geschwindigkeit in der Länge bewegt es sich in das Loch:



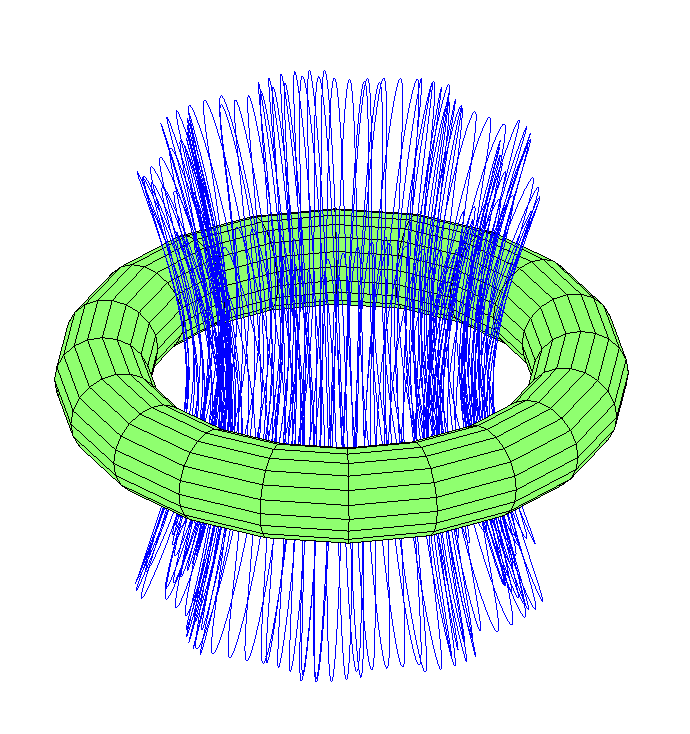
Was ist mit Flugbahnen, die durch ein Loch in eine Richtung verlaufen? Es stellte sich heraus, dass es einige Achtbahnen gibt, die eine große Ringkugel ziehen.





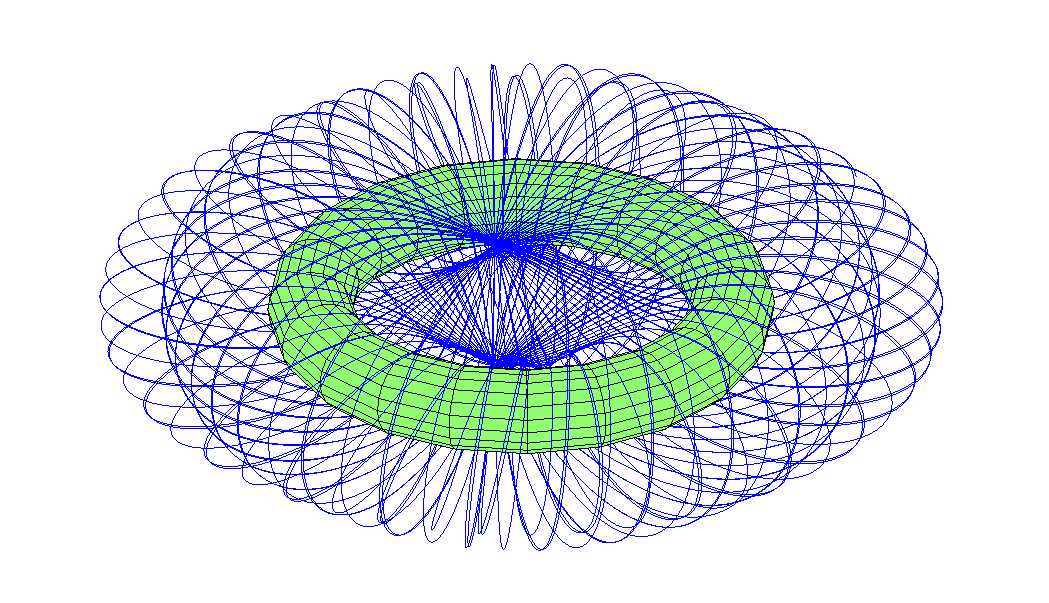
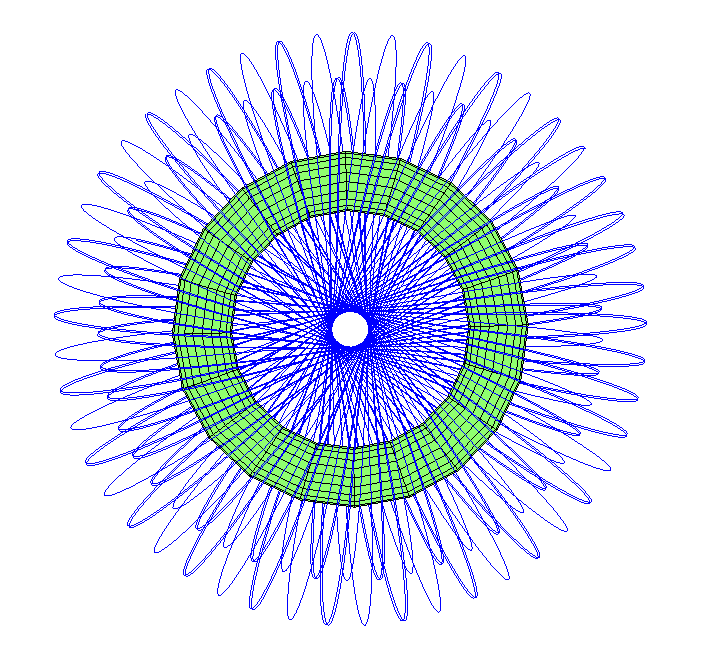
Beachten Sie, dass die Umlaufbahn leicht verlängert ist. Vom „Apogäum“ über dem äußeren Äquator geht es durch ein Loch, das auf der Rückseite erscheint, wo es an einem Punkt gegenüber dem ursprünglichen ein Perigäum erfährt. Dann geht es wieder durch das Loch und geht neben der Stelle, an der es sich zu bewegen begann - aber die Präzession dreht es entlang des Torus.

Diese Simulationen sollten als primäre Entwürfe betrachtet werden - echte Berechnungen erfordern eine höhere Genauigkeit. Meine numerische Genauigkeit reicht nicht aus, um die Langzeitstabilität zu bewerten. Die Gravitationsfelder von Donut und Hoop sehen aufgrund ihrer Abflachung noch komplizierter aus, und die Sonne und andere Planeten werden ebenfalls dazu beitragen.

Gezeitenkräfte

Gezeitenkräfte sind ein Problem. Stellen Sie sich einen Mond vor, der sich um einen Toroid bewegt. Dahinter bildet sich eine Schwellung von Wasser und Stein. Eine schnelle Rotation drückt die Schwellung des Mondes nach vorne (wenn sich der Mond in Drehrichtung des Planeten bewegt und sich über der geostationären Umlaufbahn befindet). Die Anziehungskraft der Ausbuchtung zieht den Mond selbst nach vorne und beschleunigt ihn - und im Weltraum bewegt sich der Mond in einer höheren Umlaufbahn. Auf diese Weise nahm der Mond viel Drehimpuls der Erde an, verlangsamte seine Rotation und entfernte sich von ihr. Bei schneller Rotation wie bei unseren Toroiden wird der Effekt deutlicher: Die Monde fliegen vom Planeten weg und gehen wahrscheinlich verloren.

Was passiert mit den Monden, die sich nahe der geostationären Umlaufbahn befinden? Sie bewegen sich schneller als Blähungen, was sie verlangsamt. Die Umlaufbahn wird fallen. Bald werden sie sich nach unten drehen und sich in riesige Meteore verwandeln. Das gleiche passiert mit Monden, die sich in die entgegengesetzte Richtung bewegen. Wenn der Mond groß genug ist, können ihn die Gezeitenkräfte brechen und in einen Ring verwandeln.

Breitere Bahnen, die durch das Loch verlaufen, verlieren wahrscheinlich an Stabilität. Pendelbahnen erhalten aufgrund einer Schwellung einen Drehimpuls, und der Mond bewegt sich immer schneller, bis er vom Planeten wegfliegt oder fällt. Etwa acht Umlaufbahnen können zu gleichen Teilen in Resonanz eintreten und Energie gewinnen und verlieren, aber ein ähnliches Problem wird auf sie warten. Die Toroiden werden also höchstwahrscheinlich keine wirklich exotischen Monde haben. Niemand verbietet jedoch den Start künstlicher Satelliten mit Orbit-Unterstützung. Pendelbahnen können nützlich sein, um Satelliten auf der Innenfläche eines Torus zu kommunizieren.

Zusammenfassung

Es ist unwahrscheinlich, dass torusförmige Welten auf natürliche Weise erscheinen. Aber wenn doch, werden sie erstaunliche Orte sein, um nach Abenteuern zu suchen. Große Oberfläche. Regionen mit sehr unterschiedlichen Klimazonen, Jahreszeiten, Schwerkraft und Ökosystemen. Erstaunlicher Himmel im Inneren. Ungezügeltes Wetter. Mond in seltsamen Bahnen.

Es wäre schön zu lernen, wie man sie nicht nur in Simulationen erstellt.

Anders Sandberg ist Forscher, Gelehrter, Zukunftsforscher, Transhumanist und Schriftsteller. Er promovierte in Computational Neurobiology an der Universität Stockholm und ist derzeit Fellow an der James Martin Research Society der University of Future Humanity der Universität Oxford.