Das Universum begann nicht mit dem Urknall, sondern mit dem Urtau

Kosmologische Konstante und Erschaffung des Universums

In Bezug auf das Universum gibt es zwei besonders schmerzhafte ungelöste Rätsel, von denen eines mit seinem endgültigen Schicksal zusammenhängt und das zweite - mit dem Anfang, faszinierende Kosmologen seit Jahrzehnten. Die wissenschaftliche Gemeinschaft hat immer geglaubt, dass diese beiden Aufgaben unabhängig voneinander sind - aber was ist, wenn dies nicht der Fall ist?

Die erste Aufgabe hängt mit der Existenz von etwas zusammen, das als „dunkle Energie“ bezeichnet wird und heute die Expansion des Universums beschleunigt und letztendlich sein endgültiges Schicksal bestimmt. Theoretiker sagen, dass die Wirkung der Dunklen Energie durch die Einführung eines neuen Begriffs in die Einsteinschen Gleichungen erklärt werden kann, der als "kosmologische Konstante" bezeichnet wird. Damit diese Erklärung funktioniert, muss die kosmologische Konstante einen bestimmten, sehr kleinen Wert haben. In natürlichen Einheiten wird es durch eine Einheit bestimmt, die durch eine Zahl mit 123 Ziffern geteilt wird! Eine Erklärung des Wertes dieser Konstante ist eines der schwierigsten Probleme der theoretischen Physik.


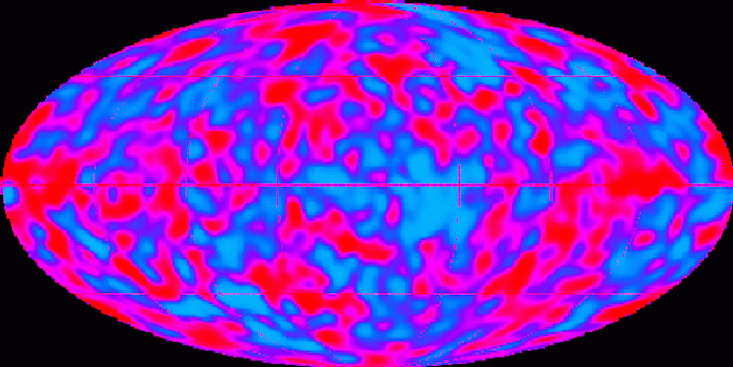CMB-Variationen zeigen Dichteschwankungen im frühen Universum an

Das zweite Problem hängt mit einer anderen wichtigen Zahl zusammen, die unser Universum definiert, und mit der Bildung von Strukturen wie Galaxien und Galaxiengruppen. Wir wissen, dass das frühe Universum, obwohl es sehr homogen war, kleine Dichteschwankungen enthielt, die zu den Hauptursachen der kosmischen Strukturen wurden, die wir heute sehen. Um mit unseren Beobachtungen übereinzustimmen, mussten diese Schwankungen eine bestimmte Größe und Form haben. Wie diese Schwankungen in den frühesten Perioden der Entwicklung des Universums auftraten, und ihre Form und Größe, ist ein ebenso erstaunliches Geheimnis der Kosmologie.

Angesichts der allgemein akzeptierten Herangehensweise an die Kosmologie werden diese beiden Zahlen - die Größe der kosmologischen Konstante und die Größe der anfänglichen Störungen - nicht als verwandt angesehen. Immerhin befasst sich einer von ihnen mit der frühesten Phase des Universums und der zweite mit der neuesten, und sie sind durch die kosmische Zeit von 14 Milliarden Jahren getrennt. Darüber hinaus erklärt die Standardkosmologie diese Werte nicht auf der Grundlage grundlegender Prinzipien. Die allgemein akzeptierten Modelle des Universums sagen nichts über den numerischen Wert der kosmologischen Konstante aus oder sagen völlig andere Werte voraus. In Bezug auf das Ausmaß der anfänglichen Störungen besteht der beliebteste Ansatz darin, diesen Wert aus der Klasse von Modellen zu erhalten, die die Inflation beschreiben - eine Phase schnellen Wachstums in der frühen Phase der Existenz des Universums. Das Problem bei Inflationsmodellen besteht darin, dass sie angepasst werden können, um fast jedes Ergebnis zu erzielen, weshalb ihnen eine Vorhersagefähigkeit fehlt.

In meiner jüngsten Arbeit mit meiner Tochter Hamsa Padmanabhan und Tomalla Fellow an der Zürcher Schweizerischen Hochschule werden beide Zahlen mit der Kosmogenese - der Erschaffung des Universums - in Verbindung gebracht und ihre genaue Bedeutung erklärt. Unsere kürzlich in Physics Letters B veröffentlichte Arbeit zeigt, dass die Existenz einer kosmologischen Konstante sowie ihr winziger Wert als direkte Folge des Informationsgehalts der Raumzeit dargestellt werden können [Padmanabhan, T. & Padmanabhan, H. Kosmische Information, die kosmologische Konstante und die Amplitude der Urstörungen. Physics Letters B 773, 81 & ndash; 85 (2017)]. Darüber hinaus liefert die Analyse den richtigen Wert für die Größe und Form kleiner Schwankungen des frühen Universums.

Die bemerkenswerte Verbindung dieser fundamentalen Konstanten ist für unser Verständnis des Universums von wesentlicher Bedeutung. Insbesondere verändert es unser Verständnis des Urknalls und macht eine Inflationsperiode in den frühen Stadien des Universums überflüssig.

Der Urknall ist wahrscheinlich das bekannteste Merkmal der Standardkosmologie. Aber er wird auch nicht wirklich für sie gebraucht. Das klassische Modell des Universums, das durch Einsteins Gleichungen beschrieben wird, funktioniert unter den Bedingungen des Urknalls bei unendlicher Dichte und Temperatur nicht mehr - dies ist die Situation, die Physiker als Singularität bezeichnen.

Aber was wäre, wenn es keine Singularität gäbe? Seit den 1960er Jahren arbeiten Physiker daran, das Universum ohne Urknall zu beschreiben, und versuchen, Gravitationstheorie und Quantentheorie zu etwas zu kombinieren, das als "Quantengravitation" bezeichnet wird. Die Physiker John Wheeler und Bryce DeWitt haben diese Ideen als erste auf die hypothetische dogometrische Phase des Universums angewendet, in der die Konzepte von Raum und Zeit noch nicht aus einer unbekannten Struktur hervorgegangen sind. Dies führte zur Entstehung der Quantenkosmologie, in der Physiker versuchen, die Dynamik einfacher Spielzeugmodelle des Universums in Quantensprache zu beschreiben. Unnötig zu erwähnen, dass im Laufe der Jahrzehnte plötzlich verschiedene, wenn auch verwandte Ideen zur Beschreibung der vorgeometrischen Phase aufgetaucht sind. Was sie verbindet, ist, dass das klassische Universum ohne Singularität durch eine Reihe von Transformationen von der vorgeometrischen Phase zu der Phase erscheint, in der Raum-Zeit durch Einsteins Gleichungen beschrieben wird. Die Hauptschwierigkeit bei der Erstellung einer solchen Beschreibung besteht darin, dass wir keine vollständige Theorie der Quantengravitation haben, die es uns ermöglichen würde, die vorgeometrische Phase im Detail zu modellieren.


Einstein nannte seine Abhängigkeit von der kosmologischen Konstante mehrmals einen groben Fehler in seinen Gleichungen. Heute glauben Physiker, dass es eine positive Bedeutung hat.

Der Hauptbestandteil, den wir eingeführt haben, um diese technische Komplexität zu umgehen, ist das Konzept der Weltrauminformation. In jüngster Zeit wird die Idee, dass Informationen eine Schlüsselrolle bei der Beschreibung der Physik spielen sollten, immer mehr unterstützt. Es tritt in mehreren Fällen auf, wenn Wissenschaftler versuchen, die Prinzipien der Quantentheorie und der Schwerkraft zu kombinieren - zum Beispiel bei der Untersuchung von Quanten-Schwarzen Löchern. In einigen dieser Modelle gibt es auch eine faszinierende Idee der Holographie, die besagt, dass der Informationsgehalt einer großen Region mit dem Informationsgehalt ihrer Grenzen in Beziehung gesetzt werden kann. Leider ist die mathematische Beschreibung der Informationen in verschiedenen Fällen unterschiedlich, und das in allen Fällen anwendbare einheitliche Prinzip wurde noch nicht gefunden. Um die Idee der Information auf das gesamte Universum anzuwenden, mussten wir daher zunächst eine physikalisch angemessene Definition dafür finden.

Die Definition der von uns verwendeten Rauminformationen kann analog beschrieben werden. Wenn ein Stück Eis schmilzt und sich in Wasser verwandelt, kommt es zu einem Phasenübergang von fest zu flüssig. Tatsächliche Phasenübergangsprozesse können äußerst komplex sein, aber die Gesamtzahl der Eisatome entspricht der Anzahl der Wasseratome. Diese Zahl bestimmt die Anzahl der Freiheitsgrade des Systems, die sich während des Phasenübergangs nicht ändern. Ebenso kann der Phasenübergang, der zum Erscheinen des Universums führte, durch eine Zahl beschrieben werden, die die Anzahl der Freiheitsgrade in der vorgeometrischen Phase mit dem Betrag in Beziehung setzt, der der klassischen Raumzeit innewohnt. Mit dieser Zahl, die wir CosmIn nannten, können wir die beiden Phasen des Universums kombinieren und die Komplexität des vollständigen Modells der Quantengravitation umgehen.

Cosmin als physikalisch beobachtbare Zahl muss endlich sein. In Ermangelung von Singularitäten glauben wir, dass alle physikalischen Größen endlich sein sollten. Darüber hinaus konnten wir zeigen, dass Cosmin nur dann endlich ist, wenn das Universum in der späten Existenzperiode eine beschleunigte Expansionsphase erlebt - wie wir es heute beobachten. Dieser Zusammenhang weist nicht nur auf die Existenz eines fundamentalen Grundes für die Existenz einer kosmologischen Konstante hin, sondern auch auf die Methoden zur Berechnung ihres numerischen Wertes - wenn wir den Wert des Kosmins kennen.

Der Wert von Cosmin in der vorgeometrischen oder Quantengravitationsphase des Universums kann anhand der Ergebnisse bestimmt werden, die periodisch in verschiedenen Modellen der Quantengravitation auftreten. Es stellt sich heraus, dass die Gesamtmenge an Informationen, die von der Quantengravitationsphase in die klassische Phase übertragen wird, einer einfachen Zahl entsprechen sollte: 4π, die Fläche einer Kugel mit Einheitsradius. Mit dieser Tatsache können wir den numerischen Wert der kosmologischen Konstante mit der Energieskala in Beziehung setzen, auf der das Universum von der Quantengravitationsphase zur klassischen überging.

Diese Energieskala des Übergangs kann mit der zweiten mysteriösen Eigenschaft unseres Universums in Verbindung gebracht werden: der Größe der winzigen Quantenfluktuationen im frühen Universum, die gewachsen sind und die Galaxien und galaktischen Cluster gebildet haben, die wir heute sehen. Ein beliebtes System zur Berechnung der Größe dieser Schwankungen verwendet Inflationsmodelle des Universums, die das Universum beschreiben, das eine unglaublich große und schnelle Größenerweiterung durchläuft. Aber es gibt viele Inflationsmodelle und sie sind sehr unterschiedlich und können jeden gewünschten Wert ausgeben. Es ist auch erwähnenswert, dass die Form der anfänglichen Schwankungen 1970 von Edward Robert Harrison (und unabhängig von Jacob Zeldovich) erhalten wurde und als Harrison-Zeldovich-Spektrum bezeichnet wird. Aber die Leute vergessen darauf hinzuweisen, dass Harrison sein Ergebnis mehr als zehn Jahre vor der Erfindung der Inflationsmodelle erhalten hat!

Unser Modell ermöglicht es uns, beide Größen - den Wert der kosmologischen Konstante und die Größe der anfänglichen Schwankungen - mit der Energieskala in Beziehung zu setzen, auf der das vorgeometrische Universum einen Phasenübergang erlebte und zum klassischen Universum wurde, in dem wir leben. Und Aufmerksamkeit, wenn wir die richtige Energieskala auswählen, erhalten wir den richtigen beobachteten Wert für diese beiden Werte. Dies führt uns zu einer algebraischen Beziehung zwischen der kosmologischen Konstante, der Größe der anfänglichen Schwankungen und der kosmischen. Wir können diese Beziehung unter Verwendung der beobachteten kosmologischen Parameter umdrehen und prüfen, ob der Cosmin-Wert wirklich 4π beträgt. Die Theorie besteht den Test perfekt; Wir finden, dass der aus Beobachtungen ermittelte Cosmin 4π mit einer Genauigkeit von 1/1000 beträgt.

Überraschenderweise hat eine komplexe Kombination von kosmologischen Parametern, die als nicht miteinander verbunden angesehen werden, eine so einfache Bedeutung. Ein üblicher Ansatz wäre es, eine solche Beziehung als zufälligen Zufall zu betrachten. Wir glauben, dass sie uns etwas Tiefes und Schönes über unser Universum erzählt.

Wir glauben, dass wir den ersten Versuch unternommen haben, den numerischen Wert der kosmologischen Konstante mit der Größe der Schwankungen im frühen Universum in Beziehung zu setzen und diese beiden Werte aus einem Modell zu erhalten, das keine einstellbaren Parameter hat, und sie mit der Energieskala zu verknüpfen, auf der das Universum zu existieren begann.

All diese Ideen existieren auf einer allgemeineren Plattform der Quantengravitation, eine Theorie, die Physiker trotz fast fünf Jahrzehnten Entwicklung immer noch nicht haben. Einer der Vorteile unseres Modells besteht darin, dass es keine Details der Quantengravitation erfordert. Sie macht jedoch zwei wichtige Hinweise auf die Natur der Quantengravitation und die Struktur der Raumzeit. Erstens sagt sie, dass Raum-Zeit so dargestellt werden muss, dass sie aus mikroskopischen Freiheitsgraden besteht, sowie aus Materie, die aus Atomen besteht. Zweitens argumentiert sie, dass die korrekte Theorie des Ursprungs des Universums einen Phasenübergang von der vorgeometrischen Phase zur klassischen Phase beinhalten sollte.

Diese Tipps können eine Schlüsselfrage beantworten: Warum haben Theoretiker nach mehreren Jahrzehnten der Arbeit Gravitation und Quantentheorie nicht kombiniert? Wir glauben, dass dies am besten durch eine andere Analogie erklärt werden kann. Wir wissen, dass die Fluiddynamik eine konsistente physikalische Theorie ist, die durch eine Reihe von Gleichungen ausgedrückt wird. Wenn wir sie als grundlegend betrachten und die Prinzipien der Quantentheorie auf sie anwenden, können wir ein neues interessantes Phänomen entdecken - zum Beispiel Phononen (Schwingungsquanten) und ihre Wechselwirkungen. Mit diesem Ansatz werden wir jedoch nicht in der Lage sein, zur Quantenstruktur der Materie zu gelangen.

Es gibt Hinweise darauf, dass Gleichungen, die die Schwerkraft in diesem Sinne beschreiben, der Fluiddynamik ähnlich sind. Mit anderen Worten, die Neuformulierung der Schwerkraftgleichungen unter Verwendung der Prinzipien der Quantentheorie ähnelt der Anwendung von Quantenprinzipien auf Gleichungen der Fluiddynamik. Wir werden die Quantenstruktur der Raumzeit auf diese Weise nicht entdecken - und wir glauben, dass Versuche, Einsteins Theorie zu quantifizieren, aufgrund dieses Jahrzehnts zu einem lauten Scheitern führten.

Stattdessen müssen wir die Natur der Schwerkraft überdenken und verstehen, was sie über die mikroskopische Struktur der Raumzeit aussagt. Der Physiker Ludwig Boltzmann nutzte diesen Ansatz, um zu verstehen, dass Temperaturphänomene den Begriff der Materie erfordern, die aus diskreten Freiheitsgraden (mit anderen Worten Atomen) besteht. Boltzmann sagte tatsächlich, wenn etwas heiß sein kann, sollte es mikroskopische Freiheitsgrade enthalten.

Raumzeit kann auch eine Temperatur haben und bestimmten Beobachtern heiß erscheinen. Diese Idee entstand dank der Arbeit von Jacob Beckenstein und Stephen Hawking im Kontext der Schwarzen Löcher. Kurz darauf, Mitte der 70er Jahre, zeigten die Arbeiten von Bill Unrich und Paul Davis, dass dies die Haupteigenschaft der Raumzeit ist. Indem Sie das Boltzmann-Paradigma mit der Tatsache kombinieren, dass Raumzeit - wie gewöhnliche Materie - heiß sein kann, kommen Sie zu dem Schluss, dass Raumzeit innere Freiheitsgrade haben muss, wie Atome in Materie. Theoretische Beweise für diese Schlussfolgerung haben in den letzten Jahren begonnen [Padmanabhan, T. Die Atome der Raumzeit und die kosmologische Konstante. Journal of Physics: Konferenzreihe 880, 012008 (2017)]. Diese Beobachtung enthält den Schlüssel zum Verständnis der Mikrostruktur der Raumzeit, was schnell zu bemerkenswerten Ergebnissen führt.

Erstens kann die Entwicklung einer Raum-Zeit-Site in Form von Freiheitsgraden (oder gleichwertig Informationsinhalten) beschrieben werden, die sich innerhalb der Grenzen dieser Site befinden. Zweitens wird die Schwerkraft unempfindlich gegenüber Änderungen bei einem Energieniveau von Null. In Einsteins Theorie ist die Schwerkraft für die absolute Energiemenge verantwortlich, weshalb es fast unmöglich ist, die kosmologische Konstante zu berechnen. Für ein Paradigma, das auf Informationsinhalten basiert, ist dies jedoch nicht der Fall. Drittens legt der Informationsansatz nahe, dass wir uns die kosmische Evolution nicht nach einer bestimmten Lösung von Einsteins Gleichungen vorstellen sollten. Diese Gleichungen ergeben sich aus einem genaueren Satz von Gleichungen, die die Quantenfreiheitsgrade der Raum-Zeit beschreiben [Padmanabhan, T. Verstehen wir den Kosmos wirklich? Comptes Rendus Physique 18, 275 & ndash; 291 (2017)].

Der Informationsansatz, der durch unser Kosminmodell bestätigt wird, gibt uns ein neues, lebendiges Bild des Universums, ähnlich einem großen Stück Eis, das eine Wärmequelle enthält. Eine Wärmequelle schmilzt das Eis um sie herum und erzeugt einen Wasserabschnitt, der sich ausdehnt und ein lokales thermodynamisches Gleichgewicht erreicht. In großem Maßstab, näher an der Phasengrenze, haben die Moleküle noch kein Gleichgewicht erreicht, da ein Stück Eis von innen erwärmt wird. Interessanterweise ist dies dem Verhalten unseres Universums sehr ähnlich. Eine Wasserfläche ähnelt dem beobachtbaren Universum (beschrieben durch Einsteins Theorie). Es ist von einer vorgeometrischen Phase (ähnlich wie Eis) umgeben, die durch bisher unbekannte Gesetze der Quantengravitation beschrieben wird. Die Idee des Urknalls verschwindet und stattdessen erscheint ein Übergang von einer Phase zur anderen entlang ihrer Grenze. Die Notwendigkeit einer Inflationsperiode verschwindet ebenfalls.

Die gesamte Plattform ist einfach und elegant, da sie durch einen einzigen Parameter beschrieben wird: die Energieskala des Phasenübergangs des frühen Universums von der Vorgeometrie zur Einsteingeometrie. Dies unterscheidet sich von herkömmlichen Inflationsmodellen, die viele Parameter enthalten und keine Vorhersagefähigkeiten haben. Unser Modell verwendet keine nicht verifizierte Physik. Das einzige Postulat, das wir gemacht haben, ist, dass der Inhalt des Universums gleich 4π sein sollte, der Oberfläche einer einzelnen Kugel.

Die Arbeit eröffnet drei neue Forschungsbereiche. Zunächst lädt sie uns ein, die Physik der vorgeometrischen Phase in verschiedenen Modellen der Quantengravitation zu untersuchen. Zweitens bietet es die Möglichkeit, die Idee der in dieser Arbeit verwendeten Rauminformationen zu untersuchen und zu versuchen, sie mit anderen ähnlichen Ideen zu verbinden, die in anderen Kontexten verwendet werden. Drittens bekräftigt es die Idee, dass Raumzeit aus elementareren Freiheitsgraden besteht - genau wie Materie aus Atomen besteht - und ermutigt uns, die verschiedenen Phasen der Raumzeit auf dieselbe Weise zu untersuchen, wie wir die verschiedenen Phasen der Materie in der Physik der kondensierten Materie untersuchen.

Tanu Padmanabhan ist Professor am Interuniversitären Zentrum für Astronomie und Astrophysik Indiens.