Wie man sich zusätzliche Dimensionen vorstellt: eindimensionale Welten

Wenn ich mit einer Person außerhalb der Physik über mögliche zusätzliche Dimensionen des Raums spreche, die uns unbekannt sind, lautet eine der am häufigsten gestellten Fragen: „Wie stellen Sie sich zusätzliche Dimensionen vor? Ich kann mir nur drei vorstellen und verstehe nicht, wie ich weiter gehen soll. es macht für mich keinen Sinn. "

Was wir Physiker nicht tun (zumindest hat keiner meiner Bekannten behauptet, dies zu tun), so stellen wir uns keine zusätzlichen Dimensionen vor. Mein Gehirn ist genau wie Ihr Gehirn begrenzt, und obwohl dieses Gehirn leicht ein dreidimensionales Bild der Welt erzeugt, in der ich mich bewegen kann, kann ich es nicht zwingen, ein Bild einer vier- oder fünfdimensionalen Welt darzustellen, genau wie Sie. Mein Überleben hing nicht von der Fähigkeit ab, sich so etwas vorzustellen, daher ist es vielleicht nicht verwunderlich, dass mein Gehirn nicht darauf eingestellt ist.

Stattdessen entwickle ich (und nach unserem Gedankenaustausch auch die meisten meiner Kollegen) eine Intuition, die auf einer Kombination von Analogien, Visualisierungstricks und Berechnungen basiert. Wir lassen die Berechnungen hier weg, aber viele Analogien und Tricks sind nicht so schwer zu erklären.

Reflexionen über zusätzliche Dimensionen können in zwei Stufen erlernt werden.

1. Ein einfacher Schritt besteht darin, zu lernen, sich die Welt mit zusätzlichen Dimensionen vorzustellen oder zu beschreiben. Sie kennen bereits mehrere Möglichkeiten, dies zu tun, auch wenn Sie sich dessen nicht bewusst sind - und Sie können ein wenig mehr lernen.
2. Die schwierigere Phase besteht darin, zu lernen, wie alles in der Welt mit zusätzlichen Dimensionen funktioniert. Wie man mit einer Nadel in vier Dimensionen arbeitet und nicht in drei; ob sich die Planeten in sechs räumlichen Dimensionen in Umlaufbahnen um die Sonne bewegen werden; werden sich Protonen und Atome bilden? Hier müssen Sie ungewohnte Tricks lernen, die die Unterschiede zwischen einer Welt mit nur einer oder zwei Dimensionen und einer uns bekannten dreidimensionalen Welt darstellen und analog arbeiten.

Beginnen wir also damit, Ihnen zu helfen, sich die Welt mit zusätzlichen Dimensionen vorzustellen. Dazu müssen Sie darüber nachdenken, wie wir im Allgemeinen jede Dimension darstellen. Beginnen wir von vorne.

• Eine Welt mit null Dimensionen ist ein Punkt. Über ihn kann jetzt wenig gesagt werden, aber wir werden zu ihm zurückkehren.
• Die eindimensionale Welt ist schon sehr interessant.
• In zweidimensionalen Welten passieren viel interessantere Dinge.
• Es ist wichtig, Verwechslungen zwischen räumlichen Dimensionen und der allgemeineren Bedeutung des Wortes „Dimension“ in der gewöhnlichen Sprache sowie in Mathematik und Statistik zu vermeiden.
• Und dann werden verschiedene Beispiele für zusätzliche Dimensionen folgen, wobei der Schwerpunkt darauf liegt, was genau „zusätzlich“ bedeutet und wie es sein kann, dass es in unserer Welt Dimensionen gibt, über die wir nichts wissen.
• Wir werden auch untersuchen, wie genau diese unsichtbaren Messungen erfasst werden können.

Eindimensionale Welten

Eine Welt mit einer räumlichen Dimension ist viel einfacher als eine Welt mit drei, aber es gibt etwas, worüber man nachdenken kann. Zum Beispiel gibt es verschiedene Arten von eindimensionalen Welten. Sie haben nicht nur bestimmte gemeinsame Eigenschaften, sondern auch interessante Unterschiede.

Betrachten wir für das erste Beispiel die Messung nicht als physikalisches, sondern als allgemeineres Konzept. Dies wird Ihnen in vielerlei Hinsicht helfen, zum Beispiel Ihre Intuition von natürlichen Missverständnissen darüber abzulenken, was Dimensionen sind und wie sie funktionieren. Lassen Sie uns über das jährliche Einkommen sprechen - wie viel Geld eine Person für ein bestimmtes Jahr erhält. Dies ist eine ebenso geeignete Studiendimension wie alle anderen.

Ertragsmessung

Ihr Einkommen für das vergangene Jahr ist eine bestimmte Zahl in Ihrer Landeswährung. Es kann positiv oder negativ sein, groß oder klein; es kann wie in Abb. 1 als Punkt auf einer Linie dargestellt werden. 1, die wir den "Einkommenspunkt" nennen werden. Jeder Punkt auf der Linie repräsentiert eine mögliche Rückkehr.


Abb. 1: eine Einnahmenlinie von unendlicher Länge, deren linke Seite Verluste darstellt, deren rechte Seite Einkommen darstellt.

Was das Jahreseinkommen zu einer eindimensionalen Immobilie macht, ist (sehr grob) Folgendes:

• Die Position im Raum wird durch eine Informationseinheit angegeben: in unserem Fall durch das Einkommen.

Beachten Sie auch, dass es kontinuierlich (oder fast kontinuierlich) ist - wenn zwei Personen unterschiedliche Einkommen A und B haben, können wir ein Drittel finden, dessen Einkommen zwischen A und B liegt.

Diese beiden Tatsachen implizieren, dass sich das Einkommen entlang der Einkommenslinie kontinuierlich ändern kann und sich nach rechts oder links bewegt - entweder zu einem höheren oder einem niedrigeren Einkommen. Es gibt keine anderen Optionen.

Natürlich hat die Umsatzlinie nichts mit dem physischen Raum zu tun, in dem Sie und ich gehen können, aber dies ist immer noch eine Dimension. Und (zumindest im Prinzip) hat er kein Ende in einer der Parteien: Es gibt (im Prinzip) keine Begrenzung, wie viel Geld eine Person in einem Jahr verdienen oder verlieren kann. Diese eindimensionale Welt ist nicht so vielfältig, aber wir können dennoch einige bedeutungsvolle Fragen dazu stellen:

• Wie verteilt sich der Jahresumsatz in den USA?
• Was ist das durchschnittliche Jahreseinkommen in Japan?
• Wie ändern sich die Antworten auf diese Fragen im Laufe der Zeit?

Diese Fragen sind in der eindimensionalen Welt der Umsatzlinie sinnvoll.

Regenbogenmessung

Und hier ist eine andere, völlig andere Welt. Eine einzige Dimension bilden die Farben des Regenbogens, von Rot über Orange bis Gelb, von dort bis Grün, [Blau], Blau und Violett [Englisch sprechende Menschen haben sechs Farben in einem Regenbogen, sie emittieren kein Blau / ca. übersetzt.]. Unter diesem Gesichtspunkt bilden Farben eine eindimensionale Welt endlicher Größe. Außerhalb von Rot oder Lila gibt es unsichtbare Formen von Blumen, aber aus der Sicht Ihrer Augen endet die Messung auf ihnen. Jetzt wird es nicht in Form einer unendlichen Linie dargestellt, sondern in Form eines Segments - der „Regenbogenlinie“ in Abb. 2. Bitte verwechseln Sie es nicht mit dem Farbkreis - wenn es geschlossen ist, beginnt unsere Messung mit Rot und endet mit Lila. Auch hier wird die Position auf der Regenbogenlinie durch eine Informationseinheit (Farbe) bestimmt und ist kontinuierlich.


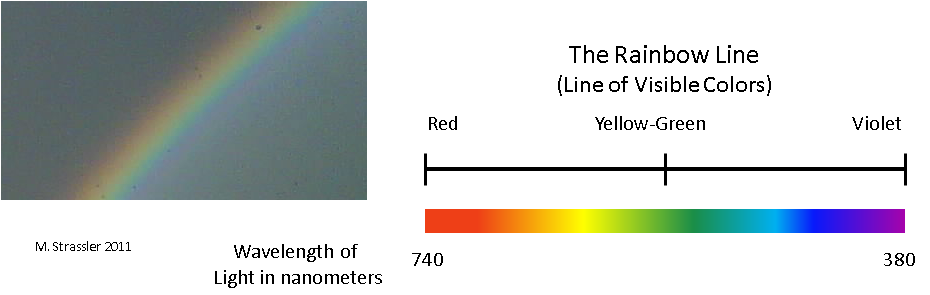Abb. 2

Dies ist natürlich auch keine Messung des physischen Raums! Sie können einen Ball von Ihrem Haus zum Haus Ihres Nachbarn werfen, aber Sie können sich nicht vorstellen, wie Sie einen Ball von grün nach orange werfen - das macht keinen Sinn. Und dennoch wird es auch eine Dimension sein. Hier können Sie viele wichtige Fragen stellen: Wie bewegt sich die Apfelfarbe entlang der Regenbogenlinie, während ein Apfel von grün nach rot gedreht wird? Wie viele im Sonnenlicht jeder der Blumen? Wenn ein orangefarbener Stern rot wird, wird er zuerst gelb?

Windrichtungsmessung

Und hier ist die dritte Messoption und noch eine. Wenn Sie sich die Wettervorhersage anhören, wird Ihnen mitgeteilt, dass der Wind bald von Norden, Nordwesten oder Südwesten weht. Mögliche Windrichtungen sind ebenfalls ein Maß. Bitte beachten Sie, dass dies keine räumliche Dimension ist! In dieser Dimension können Sie den Ball nicht so werfen, wie Sie ihn nach oben, links oder vorne werfen. Dies ist eine Messung der Richtungen im Raum!


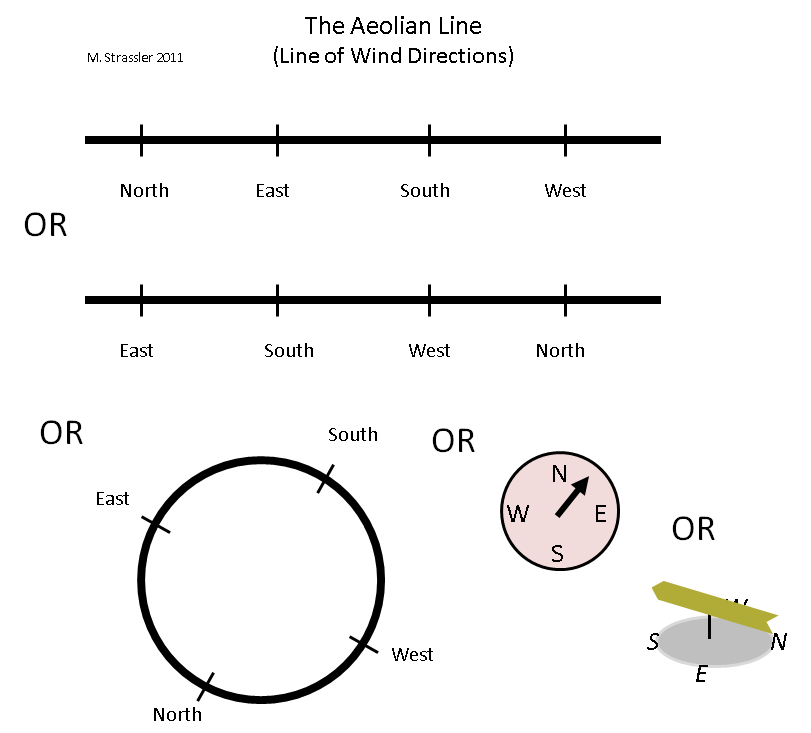Abb. 3

Wie kann diese Dimension dargestellt werden? Hierfür gibt es mindestens zwei natürliche Methoden (siehe Abb. 1). 3. Man benutzt das Segment - die "Äolische Linie" ( Aeolus ist ein Halbgott, der Herrscher der Luftelemente der alten Griechen) - aber die Äolische Linie unterscheidet sich von der Regenbogenlinie in ihrer Häufigkeit. Die Windrichtung kann sich kontinuierlich von Nord nach Ost, dann nach Süden, dann nach Westen und dann wieder nach Norden ändern. Und aus unserer Sicht kann die Linie überall geschnitten werden - vergleichen Sie die beiden Linien oben in Abb. 3, die ebenso gut die äolische Linie darstellen. Die Quintessenz ist, dass der Wind vom rechten Ende der Linie direkt zum linken Ende und umgekehrt gehen kann, sodass es keine Rolle spielt, wo er geschnitten werden soll. Oder vielleicht ist die einfachste Art, diese periodische Linie darzustellen, die Form eines Kreises. Das machen wir mit einem Kompass oder einer Wetterfahne!

Drei verschiedene eindimensionale Welten

Und hier haben Sie eindimensionale Welten. Sehen Sie, wie reich sie an Details sind! Unterschiedliche Größen, unterschiedliche Eigenschaften. Auf der Einkommenslinie kann das Einkommen für immer steigen oder fallen. Auf der Regenbogenlinie können sich Ihre Augen nur zu lila oder umgekehrt nur zu rot bewegen. Und auf der Äolischen Linie kann der Wind so viel Kreis bilden, wie Sie möchten - aber gleichzeitig kehrt er immer in eine der Richtungen zurück.

Diese Arten eindimensionaler Welten - unendlich, endlich und endlich-periodisch, dargestellt durch eine unendliche Linie, ein Segment und einen Kreis - sind die Grundzutaten für das Verständnis der Welten höherer Dimensionen. Ich werde sie mehr als einmal kontaktieren. In Abb. 4 Sie werden vorgestellt, ebenso wie der vierte Typ, der sich unendlich nur in eine Richtung erstreckt. Ein Beispiel für eine solche Messung kann die Temperatur sein: Sie kann beliebig groß sein, aber es gibt die niedrigstmögliche Temperatur - den absoluten Nullpunkt -, sodass die Temperatur eine Linie bildet, die beim absoluten Nullpunkt beginnt und von dort nach oben, aber nicht nach unten geht.


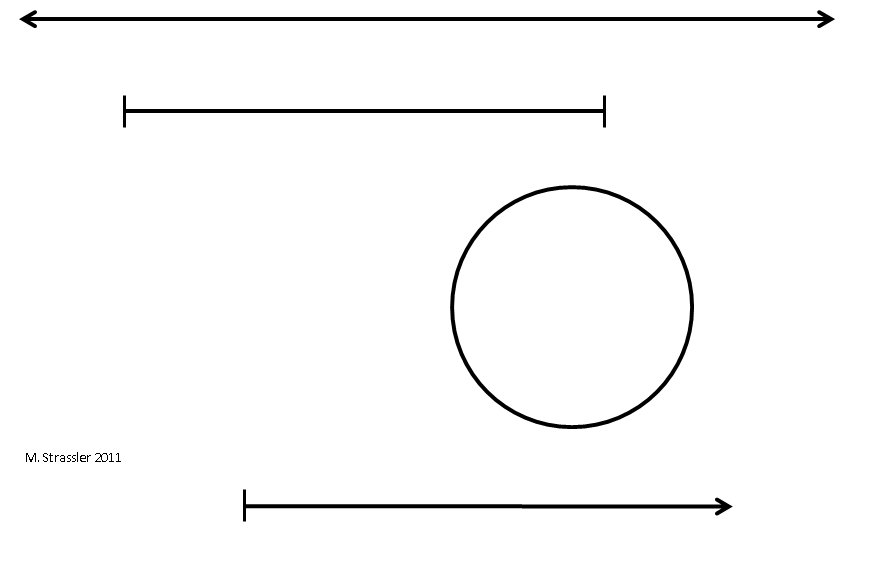Abb. 4

Wie man Dimensionen, räumliche und andere darstellt

Ich habe beiläufig verschiedene Methoden zur Darstellung von Messungen erwähnt oder angewendet. Das Einkommen kann durch eine Zahl oder eine endlose Linie dargestellt werden. Der sichtbare Regenbogen kann als Segment oder als Farbe dargestellt werden und auch eine Zahl verwenden - die Wellenlänge von Photonen, die einer bestimmten Farbe entsprechen. Die Windrichtung kann durch einen Kreis oder ein Segment dargestellt werden, dessen linkes Ende mit dem rechten verbunden ist - oder durch Wörter wie Nord, Ost, Süd, West - oder durch eine Zahl, die die Richtung in Grad von 0 bis 360 und zurück bis 0 definiert. Was wir können Die Darstellung einer Dimension auf viele verschiedene Arten gibt uns enorme Flexibilität für das Training intuitiver Arbeit mit zusätzlichen Dimensionen.

Um diese Art von Messungen zu veranschaulichen, habe ich Konzepte ausgewählt, die nichts mit dem physischen Raum zu tun haben - Einkommen, Regenbogenfarbe, Windrichtung -, um zu zeigen, dass räumliche Messungen konkrete Beispiele für ein allgemeineres Messkonzept sind. Das Verständnis dieser Tatsache erleichtert Versuche, sich Welten mit mehr als drei Dimensionen vorzustellen. Denken Sie daran, ich habe zwei Teile des Denkprozesses über zusätzliche Dimensionen erwähnt? Lerne zuerst, sie darzustellen; zweitens verstehen, wie alles funktioniert und in ihnen funktioniert. Räumliche Dimensionen weisen Merkmale auf, die damit zusammenhängen, wie einige Dinge in ihnen funktionieren, nicht jedoch mit ihrer Darstellung.

Raumwelten mit einer effektiven Dimension

Betrachten wir vor diesem Hintergrund die räumlichen Welten, denen wir regelmäßig begegnen, mit einer effektiven Dimension. Oder genauer gesagt, Situationen, in denen sich ein bestimmter Aspekt unserer Welt so verhält, als ob der Raum nur eine Dimension hat. Dann sagen wir, dass die Welt für bestimmte Teilnehmer oder Objekte effektiv eindimensional wird.


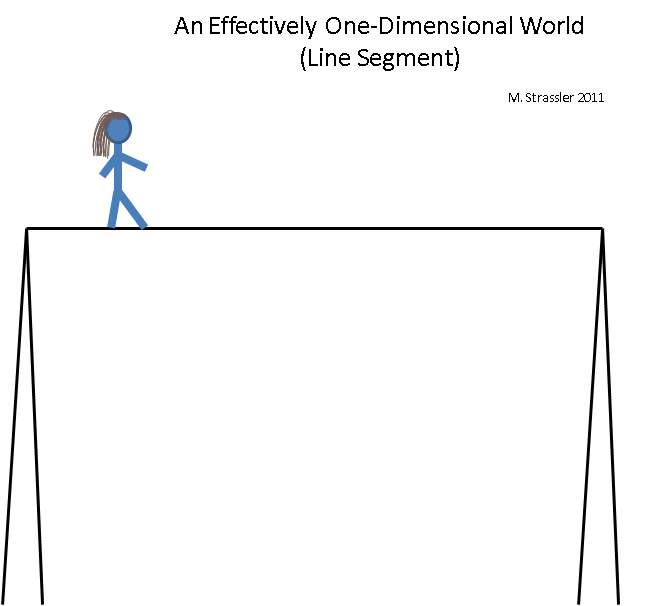Abb. 5

Stellen Sie sich einen Seiltänzer vor, der auf einem hohen Seil balanciert. Die Welt des Seiltänzers ist effektiv eindimensional (obwohl sie natürlich tatsächlich dreidimensional bleibt), da sie sich nicht sicher in eine andere Richtung als von rechts nach links oder von links nach rechts bewegen kann. Diese Welt ist wie eine Regenbogenwelt - sie ist endlich lang und wenn der Seiltänzer das Ende erreicht, muss er sich umdrehen und zurückgehen (oder vom Seil steigen, um eine Situation zu beenden, in der die Welt effektiv eindimensional wird). Was kann ich noch sagen? Die Position am Seil kann durch eine Informationseinheit bestimmt werden (z. B. den Abstand von der linken Stange zum Seiltänzer). Zwei Seiltänzer können sich auf derselben Linie treffen, aber nicht aneinander vorbeikommen.

Wir können die Welt eines Seils in eine äolische Linie verwandeln, indem wir es in einem Kreis schließen (Abb. 6). Darin konnten sich auch zwei Seiltänzer nicht passieren - dies ist die Haupteigenschaft eindimensionaler Welten. Und das wäre immer noch die letzte Dimension. Aber der Seiltänzer in einer solchen Situation konnte bereits ununterbrochen und endlos im Kreis laufen, ohne anzuhalten.


Abb. 6

Andere bekannte (effektiv) eindimensionale Welten:

• Die schmale Straße ist eine eindimensionale Welt für Autos;
• Ein schmaler Pfad mit einer Klippe - für einen Touristen, der einen Berg besteigt;
• Die Etagen eines Hochhauses sind für einen Aufzug.

Im Allgemeinen bleibt die Welt dreidimensional, aber um ein Auto, einen Touristen oder einen Aufzug zu beschreiben, muss nur eine Dimension dargestellt werden.

Denken Sie in Zukunft daran: Wir leben in einer scheinbaren dreidimensionalen Welt, und alles, was wir treffen, erscheint uns dreidimensional. Aber manchmal kann sich unsere dreidimensionale Welt (genauer gesagt ein Teil davon) so effektiv eindimensional oder zweidimensional verhalten (können Sie Beispiele nennen?) Oder sogar nulldimensional! (Jeder, der das Pech hat, jemals in einem Stau stecken zu bleiben, der sich nirgendwo bewegt, weiß, was diese Welt mit null Dimensionen ist!) Diese Intuition wird uns später sehr nützlich sein.