Die geheime Verbindung von reiner Mathematik und Physik wird enthüllt

Ein herausragender Mathematiker hat Einzelheiten darüber enthüllt, wie seine Erfolge bei der Erforschung jahrtausendealter mathematischer Probleme mit Konzepten aus der Physik zusammenhängen.

Mignon Kim

Die Mathematik ist voll von seltsamen Zahlensystemen, von denen die meisten Menschen noch nie gehört haben. Einige von ihnen werden sogar schwer vorstellbar sein. Aber rationale Zahlen sind jedem bekannt. Dies sind Zahlen zum Zählen von Objekten und Brüchen - alle Zahlen, die uns aus der Grundschule bekannt sind. Aber in der Mathematik sind manchmal die einfachsten Dinge am schwersten zu verstehen. Sie sind einfach, wie eine glatte Wand, ohne Risse und Vorsprünge oder andere offensichtliche Eigenschaften, an denen Sie festhalten könnten.

Minion Kim , Mathematiker an der Universität Oxford, interessiert sich besonders für die Frage, welche rationalen Zahlen zur Lösung von Gleichungen bestimmter Art geeignet sind. Dieses Problem hat seit Jahrtausenden Spezialisten in der Zahlentheorie angeregt. Und sie machten kaum Fortschritte auf dem Weg zu seiner Lösung. Wenn eine Frage so lange und ohne Antwort untersucht wurde, kann der Schluss gezogen werden, dass der einzige Weg, um darin voranzukommen, darin besteht, eine radikal neue Idee vorzulegen. Genau das hat Kim getan.

„Es gibt nicht viel Technologie, obwohl wir seit 3000 Jahren daran arbeiten. Wenn sich jemand eine wirklich neue Methode einfallen lässt, ist dies von großem Interesse - und genau das hat Mignon getan “, sagte Jordan Ellenberg, Mathematiker an der University of Wisconsin in Madison.

In den letzten zehn Jahren hat Kim einen völlig neuen Weg beschrieben, Muster in der scheinbar ungeordneten Welt rationaler Zahlen zu finden. Er beschrieb diese Methode in Artikeln und auf Konferenzen und gab sie an Studenten weiter, die diese Arbeit nun selbstständig fortsetzen. Aber er hat immer etwas gerettet. Seine Vision, die seine Ideen zum Leben erweckte, basierte nicht auf einer reinen Welt der Zahlen, sondern auf Konzepten, die der Physik entlehnt waren. Für Kim erinnern rationale Entscheidungen etwas an die Flugbahn des Lichts.


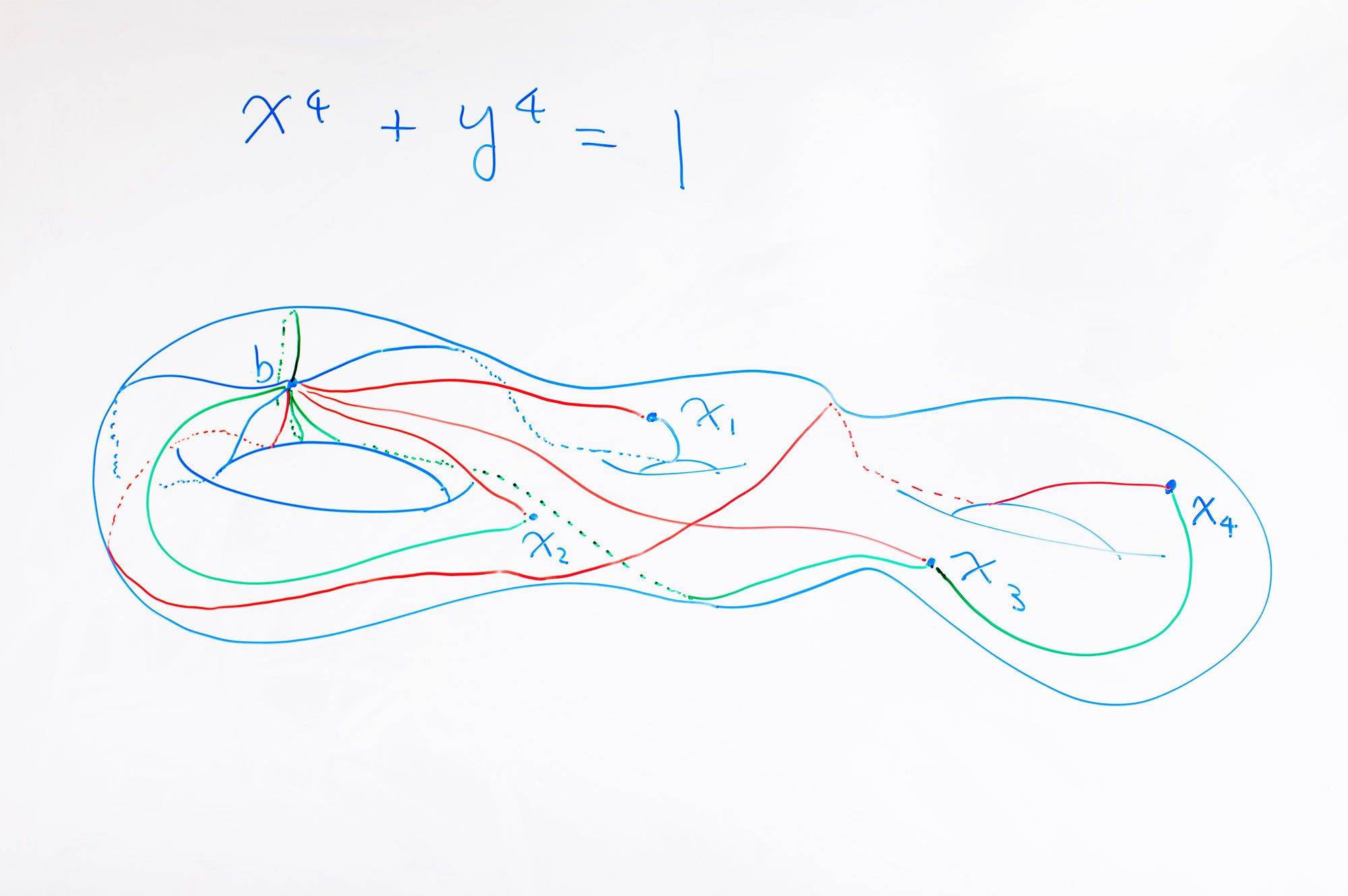Ein mathematisches Objekt, ein Drei-Loch-Torus, schmückt Kims Tafel an der Universität Oxford.

Wenn diese Verbindung fantastisch erscheint, dann auch für Mathematiker. Daher gab Kim ihre Daten lange Zeit nicht bekannt. "Ich habe es versteckt, weil mich die Verbindung zur Physik viele Jahre lang verwirrt hat", sagt er. "Spezialisten für Zahlentheorie sind sehr praktische Menschen, und der Einfluss der Physik macht sie manchmal skeptisch gegenüber der Mathematik."

Aber jetzt sagt Kim, er sei bereit, seine Vision zu teilen. "Ich denke, Veränderung ist nur ein Symptom des Alterns!" - schrieb Kim, der 53 Jahre alt wurde, in einen der ersten Briefe, die wir ausgetauscht haben, um diese Geschichte zu schreiben.

Kürzlich hielt er eine Konferenz ab, auf der Experten für Zahlentheorie und Stringtheorie zusammenkamen. Er entwarf auch Entwürfe von Artikeln, die seine Inspiration für die mathematische Gemeinschaft beschreiben sollten, und war es nicht gewohnt, über Zahlen mit solchen direkten Analogien zur physischen Welt nachzudenken.

Es bleibt nur ein Hindernis übrig - der letzte Teil der Analogie der Physik in der Mathematik, den Kim noch nicht ausgearbeitet hat. Er hofft, dass er durch die Einladung anderer, seine Vision zu teilen, insbesondere der Physiker, die notwendige Hilfe erhält, um die Arbeit abzuschließen.

Altes Rätsel

Rationale Gleichungslösungen ziehen den menschlichen Geist aktiv an. Sie bringen Zufriedenheit, ähnlich wie Sie es von den Puzzleteilen erhalten, die zusammenpassen. Daher sind sie die Helden der bekanntesten mathematischen Hypothesen.

Rationale Zahlen umfassen Ganzzahlen und jede Zahl, die als Verhältnis zweier Ganzzahlen ausgedrückt werden kann, z. B. 1, -4 oder 99/100. Mathematiker interessieren sich besonders für rationale Zahlen, die diophantinische Gleichungen lösen - Polynomgleichungen mit ganzzahligen Koeffizienten, zum Beispiel x ² + y ² = 1. Sie sind nach dem Mathematiker Diophantus benannt , der sie im 3. Jahrhundert nach Christus in Alexandria studierte.

Rationale Lösungen sind im allgemeinen Fall schwer zu finden, da sie keiner geometrischen Regelmäßigkeit entsprechen. Nehmen Sie die Gleichung x ² + y ² = 1. Ihre Lösungen in reellen Zahlen bilden einen Kreis. Entfernen Sie alle Punkte auf dem Kreis, die nicht als Brüche ausgedrückt werden können, und es bleiben nur rationale Entscheidungen übrig, die kein so ordentliches Objekt bilden. Rationale Lösungen sehen zufällig über den Umfang verteilt aus.



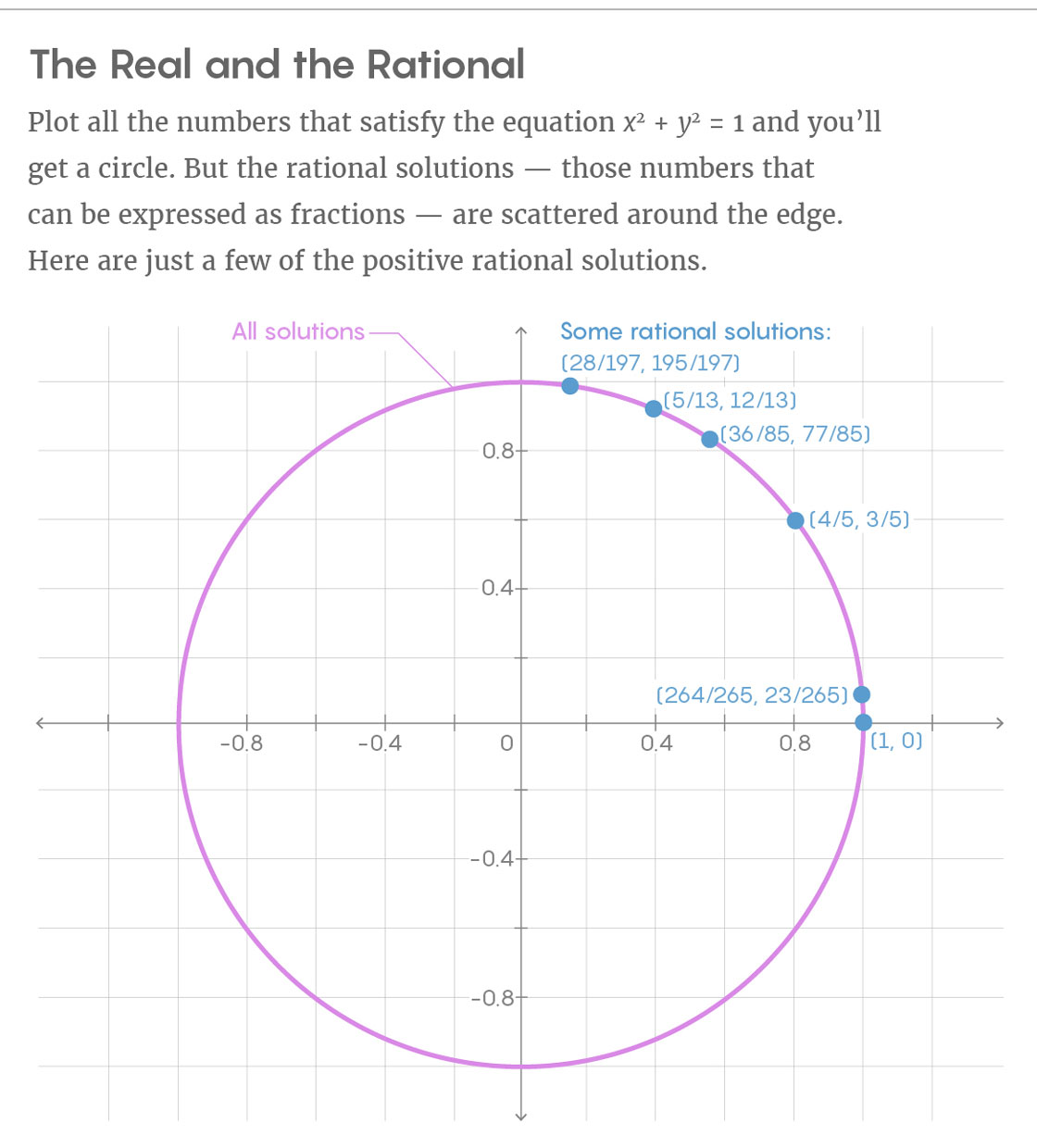
„Die Bedingung, bis zu der der Punkt gehorchen muss, um rationale Koordinaten zu haben, ist überhaupt nicht geometrisch. Es ist unmöglich, eine Gleichung zu schreiben, die rationale Punkte erfüllen müssen “, sagt Kim.

Es ist oft recht einfach, eine rationale Lösung oder sogar mehrere zu finden. Aber Mathematiker, die Understatement nicht mögen, sind mehr daran interessiert, alle rationalen Lösungen zu finden. Und das ist viel komplizierter. Es ist so schwierig, dass der Nachweis einer geringfügigen Aussage über die Anzahl der rationalen Entscheidungen ausreicht, um als mathematische Leuchte zu gelten. 1986 gewann Gerd Falting den Fields Prize , den höchsten mathematischen Preis, hauptsächlich für den Beweis der Mordell-Hypothese , wonach bestimmte Klassen diophantinischer Gleichungen nur eine begrenzte Anzahl rationaler Lösungen haben.

Faltings Beweis war ein Wendepunkt in der Zahlentheorie. Und auch nach dem, was Mathematiker als „ineffektiven Beweis“ bezeichnen, weil es nicht die genaue Anzahl rationaler Lösungen gab und sie nicht fand. Seitdem haben Mathematiker nach Möglichkeiten gesucht, diese nächsten Schritte durchzuführen. Rationale Punkte sehen in einem regulären Gleichungsgraphen zufällig aus. Mathematiker hoffen, dass durch Ändern des Kontexts, in dem sie über ein Problem nachdenken, diese Punkte zu einer sinnvollen Kombination gemacht werden können, die genau beschrieben werden kann. Das Problem ist, dass bekannte Bereiche der Mathematik keinen solchen Kontext bieten.


Kim in seinem Büro in Oxford

"Um aus rationalen Gründen effektive Ergebnisse zu erzielen, ist eindeutig eine neue Idee erforderlich", sagte Ellenberg.

Nun gibt es zwei Hauptannahmen über die Natur einer solchen Idee. Einer stammt vom japanischen Mathematiker Shinichi Motizuki , der 2012 auf der Seite seiner Fakultät an der Universität Kyoto eine komplexe und innovative mathematische Arbeit von mehreren hundert Seiten veröffentlichte. Fünf Jahre später bleibt diese Arbeit weitgehend unverständlich. Eine weitere neue Idee kam von Kim, der versuchte, sich rationale Zahlen in einem erweiterten numerischen Kontext vorzustellen, in dem ihre verborgenen Muster zu erscheinen beginnen.

Symmetrische Lösung

Mathematiker sagen oft, je symmetrischer ein Objekt ist, desto einfacher ist es, es zu studieren. Daher möchten sie das Studium diophantinischer Gleichungen unter Bedingungen platzieren, die mehr Symmetrie aufweisen als solche, bei denen dieses Problem auf natürliche Weise auftritt. Wenn dies gelingt, können sie die neu gefundenen Symmetrien verwenden, um die rationalen Punkte zu verfolgen, die sie benötigen.

Stellen Sie sich einen Kreis vor, um zu verstehen, wie Symmetrie einem Mathematiker hilft, ein Problem zu lösen. Vielleicht ist es Ihr Ziel, alle Punkte auf dem Kreis zu identifizieren. Symmetrie hilft sehr, da sie eine Karte erstellt, mit der Sie von bekannten Punkten zu Punkten wechseln können, die noch entdeckt werden müssen.

Stellen Sie sich vor, Sie haben alle rationalen Punkte am Ende eines Kreises gefunden. Da der Kreis spiegelsymmetrisch ist, können die Punkte nach oben reflektiert werden (Vorzeichenwechsel bei allen y-Koordinaten) und plötzlich alle Punkte von oben erhalten. Der Kreis hat im Allgemeinen eine so reiche Symmetrie, dass Sie, um nach allen Punkten darauf zu suchen, die Position nur eines Punktes herausfinden und ihn dann mit dem Wissen über die Symmetrie des Kreises kombinieren müssen: Sie müssen nur die unendliche Rotationssymmetrie des Kreises auf den Startpunkt anwenden.

Wenn das geometrische Objekt, mit dem Sie arbeiten, jedoch viel weniger korrekt ist, wie z. B. ein zufällig wedelnder Pfad, müssen Sie viel arbeiten, um jeden Punkt separat zu bestimmen. Sie haben keine symmetrischen Beziehungen, mit denen Sie unbekannte Punkte markieren können, wenn Hilfe berühmt.

Numerische Mengen können auch Symmetrien aufweisen. Je mehr Symmetrien in einer Menge vorhanden sind, desto einfacher ist das Verständnis. Sie können symmetrische Beziehungen anwenden, um unbekannte Werte zu erkennen. Zahlen mit bestimmten Symmetrietypen bilden eine „Gruppe“, und Mathematiker verwenden die Eigenschaften der Gruppe, um die darin enthaltenen Zahlen zu verstehen.

Viele rationale Lösungen der Gleichung müssen keine Symmetrie aufweisen und keine Gruppe bilden, weshalb Mathematiker vor der unrealistischen Aufgabe stehen, nacheinander nach Lösungen zu suchen.

Ab den 1940er Jahren begannen Mathematiker, Methoden zur Anordnung diophantinischer Gleichungen unter symmetrischeren Bedingungen zu untersuchen. Der Mathematiker Claude Chabauty entdeckte, dass innerhalb des von ihm geschaffenen größeren geometrischen Raums (unter Verwendung eines erweiterten Universums von Zahlen, die als p-adische Zahlen bezeichnet werden ) rationale Zahlen ihren eigenen symmetrischen Unterraum bilden. Er nahm diesen Unterraum und kombinierte ihn mit einer Darstellung der diophantinischen Gleichung. Die Schnittpunkte erwiesen sich als rationale Lösungen der Gleichung.

In den 1980er Jahren spezifizierte der Mathematiker Robert Coleman die Arbeit von Chaboti. In den nächsten Jahrzehnten war der Coleman-Chaboti-Ansatz das beste mathematische Werkzeug, mit dem Mathematiker rationale Lösungen für diophantinische Gleichungen finden mussten. Dies funktioniert jedoch nur, wenn der Graph der Gleichung in einem bestimmten Verhältnis mit der Größe eines größeren Raums korreliert. Wenn es gebrochen ist, wird es schwierig, die Position der Schnittpunkte der Gleichungskurve und der rationalen Zahlen genau zu finden.

"Wenn sich Ihre Kurve in einer Umgebung befindet, in der es zu viele rationale Punkte gibt, sammeln sie sich an und es fällt Ihnen schwer zu unterscheiden, welche sich auf der Kurve befinden", sagte Kiran Kedlaya, Mathematiker an der University of California in San Diego.

Und dann kommt Kim herein. Um Chabotis Arbeit zu erweitern, wollte er einen noch größeren Raum finden, in dem diophantinische Gleichungen studiert werden können - einen Raum, in dem rationale Zahlen stärker fragmentiert sind, wodurch wir Schnittpunkte mit einer großen Anzahl von Arten diophantinischer Gleichungen untersuchen können.

Räume von Räumen

Wenn Sie einen größeren Raum und einige Hinweise benötigen, wie Sie sich mithilfe der Symmetrie daran orientieren können, ist die Physik genau das Richtige für Sie.

Im allgemeinen Fall ist Raum im mathematischen Sinne eine beliebige Menge von Punkten mit einer geometrischen oder topologischen Struktur. Tausend Punkte, die vom Willen zerstreut werden oder nicht, bilden keinen Raum - sie sind nicht durch eine Struktur miteinander verbunden. Aber die Kugel, die eine zusammenhängende Organisation von Punkten ist, ist bereits Raum. Wie ein Torus oder eine zweidimensionale Ebene oder eine vierdimensionale Raumzeit, in der wir leben.

Darüber hinaus gibt es noch exotischere Räume, die man sich als „Räume der Räume“ vorstellen kann. Das einfachste Beispiel: Nehmen wir an, Sie haben ein Dreieck - und das ist Raum. Stellen Sie sich nun den Raum aller möglichen Dreiecke vor. Jeder Punkt darin repräsentiert ein bestimmtes Dreieck, und die Koordinaten dieses Punktes werden durch die Winkel des durch ihn dargestellten Dreiecks bestimmt.

Eine solche Idee ist in der Physik oft nützlich. Im Rahmen der allgemeinen Relativitätstheorie entwickeln sich Raum und Zeit ständig weiter, und Physiker betrachten jede Konfiguration von Raum und Zeit als einen Punkt im Raum aller Raum-Zeit-Konfigurationen. Räume von Räumen erscheinen auch in dem Bereich, den Physiker als Eichinvarianz bezeichnen, und arbeiten mit Feldern, die dem physischen Raum überlagert sind. Diese Felder beschreiben, wie sich Kräfte wie Elektromagnetismus und Schwerkraft ändern, wenn sie sich im Raum bewegen. Man kann sich vorstellen, dass an jedem Punkt im Raum die Konfiguration dieser Felder leicht unterschiedlich ist - und dass all diese unterschiedlichen Konfigurationen Punkte im „Raum aller Felder“ höherer Dimension bilden.

Dieser Feldraum aus der Physik ist eine Analogie zu Kims Vorschlag für die Zahlentheorie. Um dies zu verstehen, stellen Sie sich einen Lichtstrahl vor. Physiker repräsentieren Licht, das sich durch den Raum von Feldern höherer Dimension bewegt. In diesem Raum folgt Licht einem Pfad, der dem Prinzip des geringsten Widerstands entspricht und die Zeit minimiert, die erforderlich ist, um von Punkt A nach Punkt B zu gelangen. Dieses Prinzip erklärt, warum sich Licht biegt, wenn es von einem Material zum anderen bewegt wird - ein gekrümmter Pfad minimiert die Zeit Kosten.

Die größeren Räume von Räumen, die in der Physik erscheinen, weisen zusätzliche Symmetrien auf, die in keinem der Räume vorhanden sind, die sie darstellen. Diese Symmetrien lenken die Aufmerksamkeit auf bestimmte Punkte, z. B. auf einen Pfad, der die Zeit minimiert. Dieselben Symmetrien, die auf unterschiedliche Weise und in einem anderen Kontext konstruiert wurden, können an anderen Punkten hervorgehoben werden - beispielsweise an Punkten, die rationalen Gleichungslösungen entsprechen.

Symmetrie mit Physik verbinden

In der Zahlentheorie gibt es keine Teilchen, die verfolgt werden könnten, aber sie haben so etwas wie Raum-Zeit und bieten eine Möglichkeit, Pfade zu zeichnen und den Raum aller möglichen Pfade zu schaffen. Aus dieser Grundkorrespondenz entwickelt Kim Schemata, in denen "das Problem, die Flugbahn des Lichts zu finden und rationale Lösungen diophantinischer Gleichungen zu finden, zwei Gesichter desselben Problems sind", wie er letzte Woche auf einer Konferenz in mathematischer Physik in Heidelberg erklärte.

Lösungen diophantinischer Gleichungen bilden Räume - dies sind durch Gleichungen definierte Kurven. Diese Kurven können eindimensional wie ein Kreis oder mehrdimensional sein. Wenn Sie beispielsweise eine komplexe Lösung der diophantinischen Gleichung x ⁴ + y ⁴ = 1 erstellen, erhalten Sie einen Torus mit drei Löchern. Rationale Punkte auf einem solchen Torus haben keine geometrische Struktur - deshalb ist es schwierig, sie zu finden -, aber sie können mit Punkten in einem mehrdimensionalen Raum von Räumen verglichen werden, die eine solche Struktur besitzen.



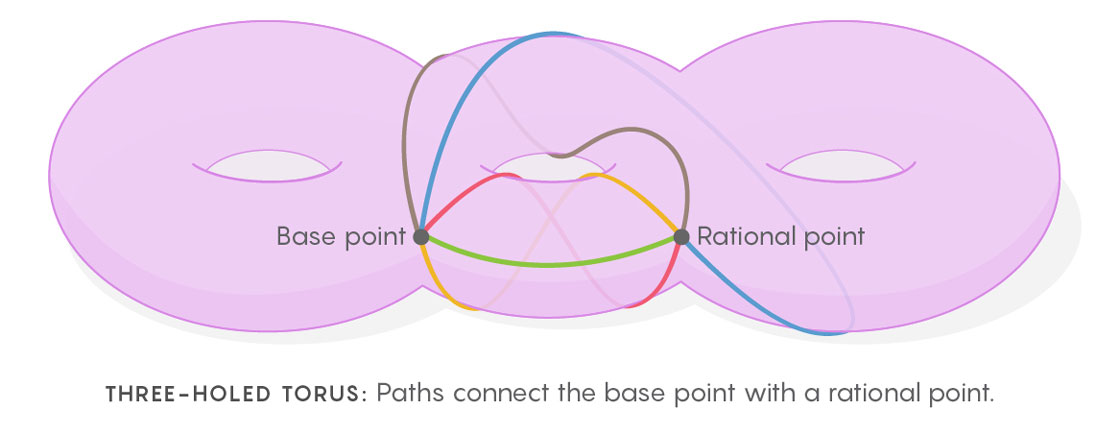
Kim schafft diesen mehrdimensionalen Raum von Räumen und stellt sich vor, wie geschlossene Kurven auf dem Torus (oder in dem Raum, der die Gleichung definiert) gezeichnet werden können. Das Verfahren zum Zeichnen von Kurven sieht folgendermaßen aus. Zuerst müssen Sie den Startpunkt auswählen, dann eine Schleife von diesem Punkt zu einem anderen zeichnen und zum ersten zurückkehren. Wiederholen Sie diesen Vorgang und zeichnen Sie die Pfade, die den Basispunkt mit allen anderen Punkten des Torus verbinden. Sie erhalten das Dickicht aller möglichen Schleifen, die am Basispunkt beginnen und enden. Diese Menge von Schleifen ist ein zentral wichtiges Objekt der Mathematik, das als grundlegende Gruppe des Raums bezeichnet wird.

Jeder Punkt auf dem Torus kann als Ausgangspunkt verwendet werden. Jeder Punkt hat ein einzigartiges Dickicht von Pfaden, die von ihm ausgehen. Jede dieser Pfadsammlungen kann als Punkt in einem mehrdimensionalen „Raum aller Pfadsätze“ (als Raum aller möglichen Dreiecke) dargestellt werden. Dieser Raum von Räumen ist geometrisch sehr ähnlich zu dem, was Physiker in der Theorie der Eichinvarianz aufbauen: Die Art und Weise, wie sich Pfadsätze ändern, wenn Sie von einem Punkt auf einem Torus zu einem anderen gehen, ist sehr ähnlich wie sich Felder ändern, wenn Sie von einem Punkt zu einem Punkt gehen ein anderer im realen Raum. Dieser Raum von Räumen hat zusätzliche Symmetrien, die sich nicht auf dem Torus selbst befinden. Und obwohl rationale Punkte auf einem Torus keine Symmetrie haben, können wir, wenn wir in den Raum aller Pfadsätze gehen, Symmetrien zwischen Punkten finden, die mit rationalen Zahlen assoziiert sind. Sie erhalten Symmetrien, die vorher nicht sichtbar waren.

"Ich sage manchmal, dass" versteckte arithmetische Symmetrie "in diesen Pfaden codiert ist, was den internen Symmetrien der Theorie der Eichinvarianz sehr ähnlich ist", sagte Kim.

Wie Chaboti findet Kim rationale Lösungen, indem er die Schnittpunkte in dem größeren Raum untersucht, den sie geschaffen haben. Er nutzt die Symmetrien dieses Raumes, um zu den Schnittpunkten zu gelangen. Er hofft, eine Gleichung zu entwickeln, die diese Punkte genau definiert.

Im physischen Kontext kann man sich alle möglichen Wege vorstellen, die ein Lichtstrahl gehen kann. Dies ist Ihr "Raum aller Pfade". Physiker interessieren sich für Punkte in diesem Raum, die Pfaden entsprechen, die die Zeit minimieren. Kim glaubt, dass die Punkte, die dem Dickicht von Pfaden entsprechen, die von rationalen Punkten ausgehen, ungefähr dieselbe Eigenschaft haben - das heißt, diese Punkte minimieren einige Eigenschaften, die auftreten, wenn Sie die geometrischen Formen diophantinischer Gleichungen betrachten. Er hat nur noch nicht herausgefunden, was diese Eigenschaft sein könnte.

"Was ich versucht habe zu finden", ist das Prinzip des geringsten Widerstands in einem mathematischen Kontext, schrieb er mir in einem Brief. "Ich habe es noch nicht gefunden, aber ich bin sicher, dass es existiert."

Unsichere Zukunft

In den letzten Monaten habe ich Kims Vision beschrieben, inspiriert von der Physik, von mehreren Mathematikern, Fans seiner Beiträge zur Zahlentheorie. Aber als sie von einem solchen Detail seiner Arbeit erfuhren, gingen sie verloren.

"Als Theoretiker repräsentativer Größen würde ich sagen, wenn mir all die erstaunlichen Errungenschaften des Minion gezeigt und gefragt würden, ob sie von der Physik inspiriert sind: Worüber zum Teufel redest du?" - sagte Ellenberg.

Bisher hat Kim in keinem seiner Werke die Physik erwähnt. Stattdessen schreibt er über Objekte, die als "Selmer-Variationen" bezeichnet werden, und untersucht die Beziehung zwischen Selmer-Variationen im Raum aller Selmer-Variationen. Solche Dinge sind Experten der Zahlentheorie vertraut. Für Kim waren sie jedoch immer nur eine andere Bezeichnung für bestimmte physische Objekte.

"Es sollte eine Möglichkeit geben, physikalische Ideen zu verwenden, um Probleme in der Zahlentheorie zu lösen, aber wir haben noch nicht genug darüber nachgedacht, wie eine solche Plattform geschaffen werden kann", sagte Kim. "Wir befinden uns in einem Zustand, in dem unser Verständnis der Physik recht gut entwickelt ist, und viele Spezialisten für Zahlentheorie sind daran interessiert, um den nächsten Schritt zu tun."

Das Haupthindernis für die Kim-Methode besteht darin, Maßnahmen zu finden, um den Platz aller Schleifensätze zu minimieren. In der physischen Welt sieht dieser Ansatz natürlich aus, aber in der Arithmetik hat er keine offensichtliche Bedeutung. Selbst die Mathematiker, die Kims Arbeit genau beobachten, sind sich nicht sicher, ob er ihn finden kann.

"Ich denke, Kims Programm wird viele wundervolle Dinge für uns tun. "Ich glaube nicht, dass wir so klar haben werden, wie Mignon verstehen will, ob rationale Punkte klassische Lösungen für die Theorie der arithmetischen Eichs sind", sagt Arnav Tripathy, Professor für mathematische Physik an der Harvard University.

Die Sprache der Physik überschneidet sich heute fast nicht mehr mit der Praxis der Zahlentheorie. Kim glaubt, dass sich dies mit ziemlicher Sicherheit ändern wird. Vor vierzig Jahren hatten Physik, Geometrie und Topologie wenig gemeinsam. In den 1980er Jahren fanden mehrere Mathematiker und Physiker, heute bedeutende Persönlichkeiten, genaue Wege, die Eigenschaften von Formen mithilfe der Physik zu untersuchen. Nach dieser Entwicklung änderte sich dieser Bereich und kehrte nicht zu den vorherigen Methoden zurück.

„Heutzutage ist es praktisch unmöglich, sich für Geometrie und Topologie zu interessieren, ohne etwas über Physik zu wissen. Ich bin mir ziemlich sicher, dass dies auch mit der Zahlentheorie geschehen wird “, sagte Kim in den nächsten 15 Jahren. "Alle Verbindungen sind äußerst natürlich."