Ich habe Ihnen bereits
einige Beispiele gegeben, wie
zusätzliche Dimensionen in der Natur dargestellt werden können - Dimensionen im Raum, von denen wir nicht einmal wissen. Bisher habe ich jedoch noch nicht erklärt, wie Wissenschaftler etwas über ihre Existenz erfahren können.
Hier können Sie mehrere grundlegende Strategien anwenden, aber ich werde mich vorerst auf eine einfache Konsequenz der Existenz zusätzlicher Dimensionen konzentrieren. Es hat einen sehr allgemeinen Charakter und führt zu einer Strategie für das Studium der Teilchenphysik, die für viele Studien relevant ist, einschließlich Experimenten am Large Hadron Collider.
Meine Erklärung wird in zwei Schritten erfolgen. In der ersten Phase, unter Verwendung der einfachsten Physik, werde ich Ihnen ein intuitives Verständnis geben, einfach, aber unvollkommen (da die Quantenmechanik darin nicht berücksichtigt wird), und ich werde eine teilweise falsche Antwort geben. Im zweiten Schritt werde ich die Ungenauigkeit korrigieren, die eine weitere zusätzliche Komplikation erfordert, und dann sehen Sie die gesamte Antwort.
Aber bevor ich mit der Erklärung beginne, werde ich Ihnen sofort eine Antwort geben, damit Sie verstehen, was ich Ihnen erklären muss. Hier ist es - auf verschiedene Weise, um es Ihnen klarer zu machen.
Jedes Teilchen, das sich in Dimensionen bewegt, die zusätzlich zu den uns bereits bekannten Dimensionen sind, wird wie Sie und ich, naive Beobachter, die keine Ahnung von zusätzlichen Dimensionen haben, Teilchen verschiedener Typen erscheinen, von denen sich jedes nur in uns bekannten Dimensionen bewegt, und die Unterschiede zwischen denen sehr klein, bis auf ihre Massen.
Mit anderen Worten: Wenn sich ein Partikel eines bestimmten Typs in allen Dimensionen bewegen kann, scheint es einem nicht informierten Beobachter, dass es in der Natur nicht nur dieses Partikel (das sich nur in den ihm bekannten Dimensionen bewegt) gibt, sondern eine ganze Reihe verwandter Partikel, jeweils „KK-Partner“ die sich auch in bekannte Richtungen bewegt, etwas anders als das ursprüngliche Teilchen, außer dass sie schwerer sind. "KK" bezieht sich auf die
Kaluza-Klein-Theorie , über die später gesprochen wird.
Angenommen, wir leben in vier räumlichen Dimensionen, von denen drei groß sind (uns bekannt) und die vierte sehr kurz ist (wie die Breite des Streifens, den ich in den vorherigen Beispielen verwendet habe). Mit kurz ist eine wirklich kurze Strecke gemeint, die kleiner ist als der Durchmesser des Protons. Nennen Sie diese Entfernung L.
Stellen Sie sich nun vor, es gibt ein Teilchen, sehr, sehr klein, kleiner als L, das sich in allen vier räumlichen Dimensionen frei bewegen kann. Wir nehmen auch die Existenz schlauer Beobachter an, die wissen, dass sich dieses Teilchen in vier Dimensionen bewegen kann und eine Masse m hat. Nun werden wir naive Beobachter betrachten, die die kleine räumliche Dimension nicht kennen und glauben, in einer dreidimensionalen Welt zu leben. Nach einigen in Abb. 1 können wir sagen: „Hier ist eine Art von Teilchen, die sich in drei Dimensionen bewegen kann und die Masse m hat; aber schauen Sie, eine andere Art von Teilchen, das sich auch in drei Dimensionen bewegen kann, und es ist dem ersten ähnlich, nur seine Masse M, viel mehr als m; und wow, hier ist eine andere Art von Teilchen, die sich in drei Dimensionen bewegen kann, ähnlich wie die erste, nur hat sie eine Masse M ', die größer als M ist; und eine andere Art von Teilchen, Masse M ”; und mehr und mehr ... "
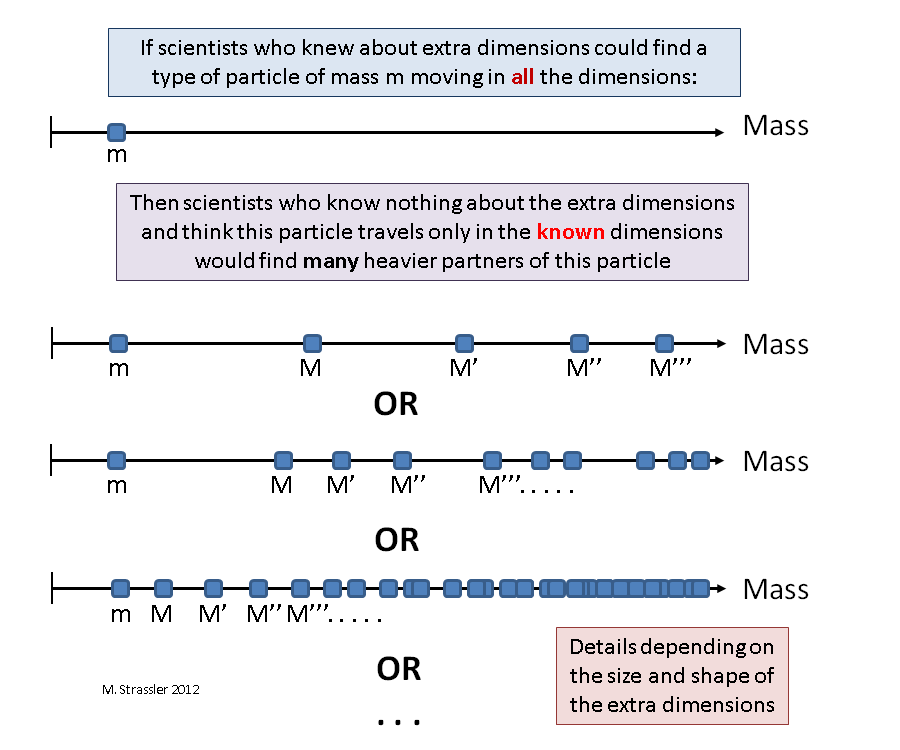 Abb. 1
Abb. 1Die Massen M, M ', M' usw. werden durch die Kombination der Grundmasse m und der Geometrie der zusätzlichen räumlichen Dimensionen bestimmt - insbesondere M, M ', M' usw. sind umgekehrt proportional zu L. Je kleiner L, desto größer M, M ', M ”und so weiter, und desto schwieriger ist es, starke QC-Partner zu finden. Darüber hinaus gibt die Reihenfolge der Massen, die in QC-Partnern auftreten, einen direkten Hinweis auf die Menge, Größe und Form zusätzlicher Messungen. Sie können eine musikalische Analogie geben - diese Tatsache beruht auf der Tatsache, dass die genauen Harmonischen, die vom Instrument erzeugt werden, Informationen über seine Form und Größe geben können.
Beispiel: Wenn sich Photonen (Lichtteilchen) in einer oder mehreren zusätzlichen Dimensionen bewegen könnten, wie ein Boot in einem Kanal, würde ein Beobachter, der zusätzliche Dimensionen kennt, sie als masselose Teilchen (m = 0) beschreiben, die sich in allen Dimensionen bewegen . Aber ein menschlicher Wissenschaftler, der bisher nur ein masseloses Photon kennt, das sich in drei bekannten Dimensionen bewegt, würde eine Reihe schwerer Teilchen entdecken, die Photonen ähnlich sind. Je kleiner die zusätzliche Messung ist, desto größer ist die Masse der KK-Photonen und desto schwieriger ist es, sie zu öffnen - genauer gesagt, je schwerer sie sind und desto mehr Energie benötigt der Teilchenbeschleuniger, um sie zu erzeugen.
Es kann durchaus sein, dass sich mehrere Partikeltypen in zusätzlichen Dimensionen bewegen können. In diesem Fall werden Wissenschaftler für jeden dieser Partikeltypen schwere KK-Partner entdecken (siehe Abb. 2). Die Entdeckung einer kleinen Anzahl schwerer Teilchen, die einigen der bekannten leichten Teilchen ähneln, deren Massenverteilung sich ähnlich wie in Abb. 1 zeigt. Die Verteilung 2 zeigt deutlich, dass die neuen Partikel QC-Partner sind und dass wir eine oder mehrere zusätzliche Dimensionen haben.
 Abb. 2
Abb. 2Dies ist die einfache Antwort: Ein Partikel, das sich sowohl in zusätzlichen als auch in bekannten Dimensionen bewegt, öffnet sich uns durch die Entdeckung seiner starken QC-Partner. Später werde ich genauer beschreiben, wie Sie versuchen können, QC-Partner im Experiment zu produzieren und zu öffnen. In den
folgenden Artikeln werde ich beschreiben, warum diese bestimmte Antwort richtig ist - und ich werde eine einfache und komplexe Version der Erklärung geben.