🐘 ✍🏼 👇🏾 Partnerschaft Kaluza-Klein-Partner, Teil 2 🍕 🏢 🤞

In einem früheren Artikel habe ich erklärt, warum es naiven Beobachtern, die sich des Vorhandenseins einer zusätzlichen Dimension nicht bewusst sind, erscheint, dass ein Partikel, das sich in zusätzlichen Dimensionen bewegen kann, Kaluza-Klein (KK) -Partner hat - schwerere Versionen des ursprünglichen Partikels. Ich wies darauf hin, dass, wenn sich das anfängliche Teilchen der Masse m in Richtung der zusätzlichen Dimension bewegt, es dem naiven Beobachter bewegungslos und schwerer erscheint, als es sein sollte, das heißt, als ob es ein Teilchen eines anderen Typs ist. Diese Klasse vermeintlich neuer Partikel, ähnlich der ursprünglichen, aber schwereren, wird als QC-Partner bezeichnet.

Wenn sich im Fall eines Streifens ein Teilchen der Masse m mit einem Moment p über den Streifen bewegt, nimmt der Beobachter, der den Streifen als Linie betrachtet, an, dass das Teilchen ein KK-Partner mit null Impuls und Masse M ist, wobei

M^{2} = m^{2} + (p_{a c r o s s} / c)^{2} > m^{2}

$M ^ 2 = m ^ 2 + (p_ {across} / c) ^ 2> m ^ 2$

Obwohl dies im Allgemeinen zutrifft, muss für jede Masse M größer als m ein eigener QC-Partner vorhanden sein. Dies ist jedoch nicht der Fall - unsere Welt ist quantenmäßig (siehe Abb. 1 des vorherigen Artikels). Jetzt finden wir genau heraus, wie die Quantenmechanik das ganze Bild verändert.

Das Hauptmerkmal der Quantenphysik, das wir benötigen, ist, dass für ein Quantenteilchen, das sich in einer endlichen Größenmessung bewegt, nicht alle möglichen Werte von p _über zulässig sind. In einer allgemeineren Formulierung: Die Quantenmechanik legt nahe, dass ein „Teilchen“, das sich in einer Messung endlicher Größe bewegt, nur bestimmte Impulswerte in dieser Richtung haben kann.

Dies ist eine der wichtigsten und seltsamsten Folgen der Quantenmechanik! Auf den ersten Blick ist dies völlig uninteressant, denn was kann Sie daran hindern, das „Teilchen“ mit dem Impuls p um eine leichte Beschleunigung zu bitten, so dass sich sein Impuls geringfügig von p unterscheidet?

Was ist ein Quantum?

Sie haben vielleicht bemerkt, dass ich angefangen habe, das Wort „Teilchen“ zu zitieren, weil wir im aktuellen Kontext den Begriff „Teilchen“, der zur Beschreibung von Elektronen, Myonen, Quarks, Gluonen und allen anderen bekannten Elementarteilchen verwendet wird, von einem intuitiven Konzept unterscheiden müssen Partikel, die wir aus unserer Erfahrung mit Staub, Sand, Salz und Kies erben. Es wäre besser, solche "Teilchen" wie ein Elektron, ein Photon, einen Quark usw. als Quanten oder schlauere Objekte zu bezeichnen. Diese Quanten sind Störungen der Felder, sie ähneln eher Wellen als Teilchen. Der beste Weg, um Quanten zu verstehen, besteht darin, sich Wellen vorzustellen. Dies ist ein weiterer wichtiger sprachlicher Punkt: Wenn ich „Welle“ sage, meine ich nicht so etwas wie eine separate Welle im Ozean, die am Ufer bricht - ich meine eine Folge von Wellen mit vielen Kämmen und Tälern.

Ein Beispiel für solche Wellen sind elektromagnetische Wellen, zu denen auch Lichtwellen gehören, die für unsere Augen unterscheidbar sind. Stellen Sie sich vor, wir hätten eine solche Welle aufgenommen - zum Beispiel Laserlicht - und das Licht immer mehr gedimmt. Wie kann es gedämpft werden? Es stellt sich heraus, dass es in unserer Quantenwelt einen möglichst schwachen Lichtblitz gibt, den wir als Lichtquant oder Photon bezeichnen. Ein Photon ist eine Lichtwelle, deren Wellenhöhe und -intensität so klein wie möglich ist. Wir verdanken all diese Konzepte und Namen Einstein, der trotz seiner bekannten Unzufriedenheit mit den konzeptuellen Konsequenzen der Quantenmechanik einer der Begründer dieser Theorie war.

Aus meiner Sicht ist es nicht intuitiv, dass Lichtwellen aus Quanten bestehen, da sich dies in keinem der Prozesse manifestiert, die wir direkt beobachten. Aber unser Körper nutzt diese Tatsache dank Prozessen, die wir nicht kennen, ständig. Das Lampenlicht scheint für unser Gehirn kontinuierlich zu sein, aber unsere Augen absorbieren die Photonen tatsächlich einzeln. Außerdem habe ich mit eigenen Augen gesehen, dass Licht aus Quanten besteht - das weiß ich nicht nur aus Büchern.

Wir Physiker nennen diese Lichtquanten oft „Lichtteilchen“, weil sie sich in vielerlei Hinsicht wie Teilchen verhalten. Jedes Photon, das sich von selbst in einer geraden Linie bewegt, hat eine bestimmte Energie und einen bestimmten Impuls. Alle Photonen haben den gleichen Massenwert (insbesondere Null). ein Photon kann nicht in kleinere Teile geteilt werden; Ein Photon kann nur vollständig emittiert oder absorbiert werden. Diese Eigenschaften entsprechen in etwa dem, was unsere Intuition von Partikeln wie Sandkörnern, Glaskugeln, Staubpartikeln usw. erwarten kann.

Aber das Wort "Quantum" ist aus vielen Gründen besser als das Wort "Teilchen", da einige Eigenschaften von Quanten den Eigenschaften von Teilchen und einige den Eigenschaften von Wellen ähnlich sind. Ein bekanntes Beispiel für Wellenverhalten ist ein Quantenweg, um gleichzeitig durch zwei Türen zu gelangen und mit sich selbst zu interagieren (in demselben Sinne, in dem Wellen miteinander interagieren und Grate mit Tälern sich gegenseitig zerstören). Und dann werden wir ein anderes Beispiel sehen.

Es muss daran erinnert werden, dass das, was für das Photon getan wird, auch für alle bekannten "Teilchen" getan wird. In der Tat ist jeder von ihnen eine Art Quantum - die Wellen mit der niedrigstmöglichen Höhe im entsprechenden Feld. Ein Elektron ist ein Quantum eines elektronischen Feldes. Quark ist ein Quantum eines Quarkfeldes. Das Z-Teilchen ist das Quantum des Z-Feldes und so weiter.

Quantums - QC-Partner

Es ist Zeit herauszufinden, was ich Ihnen zu erklären versprochen habe: Warum die Wellennatur von Quanten impliziert, dass die Partikelmassen von KK-Partnern bestimmte Werte annehmen und nicht alle möglichen Werte, große Massen m des ursprünglichen „Partikels“. Der berühmte Physiker Louis de Broglie , der den Spuren von Einsteins ersten Ideen folgte, definierte zum ersten Mal klar, dass die Beziehung zwischen Wellen, Teilchen und Quanten impliziert, dass für ein Quanten eine Beziehung besteht zwischen:
• Sein Impuls (eine Eigenschaft, die den Eigenschaften von Partikeln ähnelt),
• Und seine Wellenlänge (eine Eigenschaft, die den Eigenschaften von Wellen ähnelt) [und auch hier meinen wir mit „Welle“ eine Folge von Wellen, und die Wellenlänge bezieht sich auf den Abstand zwischen den Wellenbergen in der Folge].

Und diese Abhängigkeit wird einfach ausgedrückt: Impuls = h / Wellenlänge

h ist die berühmte Planck-Konstante , die gleiche Grundkonstante der Natur wie die Lichtgeschwindigkeit. Planck führte diese Konstante 1900 ein und versuchte, ein mysteriöses physikalisches Phänomen aufzudecken. Dies war der erste Schritt in Richtung der Quantennatur der Welt. Jedes Mal, wenn Sie versuchen, ein Phänomen zu beschreiben, bei dem die Quantenmechanik eine wichtige Rolle spielt, erscheint die Konstante h. In vielen Formeln können Sie den Wert ℏ sehen, und dies ist nur h geteilt durch 2π, da dieser Wert zur Vereinfachung der Formeln oft bequemer ist.

Abb. 1: Betrachten Sie ein Quantum, das sich entlang eines Streifens und entlang eines Rohrs bewegt

In einigen Fällen ist es etwas einfacher zu erklären, was mit dem Quantum passiert, das sich entlang des Rohrs bewegt, als mit dem, was sich entlang des Streifens bewegt, den wir in den vorherigen Beispielen verwendet haben. Fast alles, was für das Rohr funktioniert, gilt für den Streifen. Deshalb werde ich sie zusammen verwenden.

Der leichteste QC-Partner

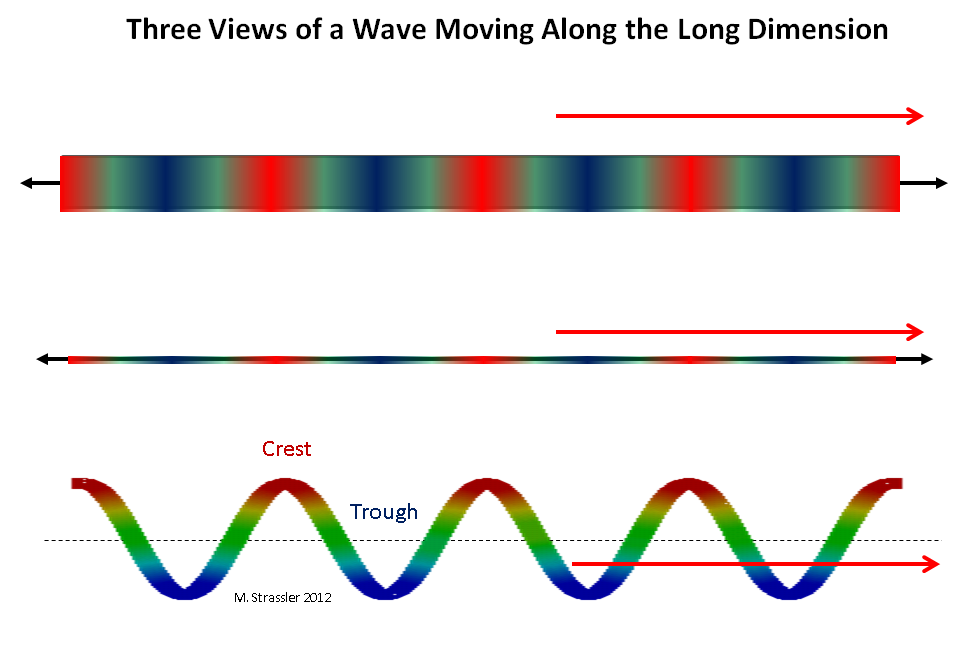Abb. 2: drei Ansichten einer Welle, die sich entlang einer langen Dimension bewegt

Stellen Sie sich ein Quantum vor, das sich entlang eines Streifens der Breite W oder entlang eines Rohrs des Kreises S bewegt. Stellen Sie sich zunächst ein Quantum vor, das sich entlang einer langen Dimension bewegt (long bedeutet unendlich oder so lang, dass es unendlich sein kann, soweit wir das beurteilen können). Eine Welle, die entlang eines Streifens oder Rohrs verläuft, kann sich entlang einer langen Dimension in jede Richtung bewegen und eine beliebige Wellenlänge haben (den Abstand zwischen zwei benachbarten Graten). Siehe Abb. 2. Ein solches Quantum kann laut de Broglie einen beliebigen Impuls entlang eines Streifens oder Rohrs haben: Der Impuls kann Null sein, sehr klein, klein, groß, in jede Richtung usw. Im Prinzip kann ein Impuls ein wenig mehr (oder ein wenig weniger) erzeugt werden, indem ein Quant in Richtung seiner Bewegung (oder in die entgegengesetzte Richtung) gedrückt wird.

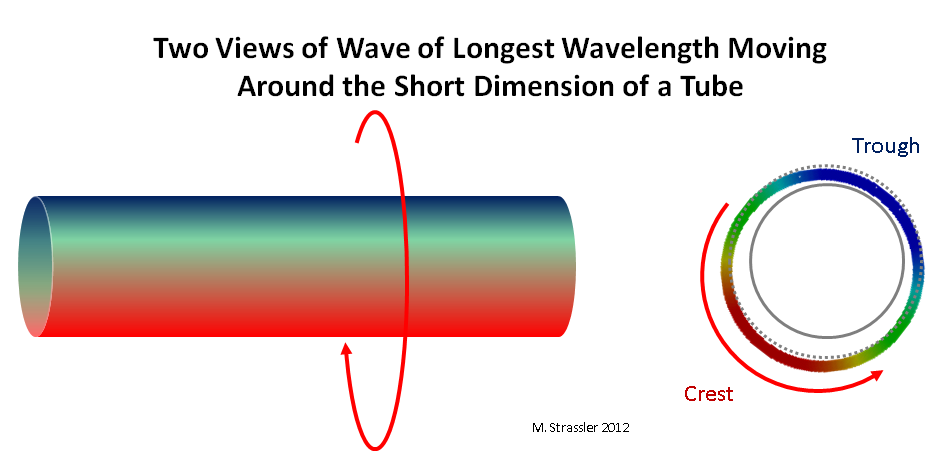Abb. 3: zwei Ansichten einer Welle, die sich entlang einer kurzen Abmessung eines Rohrs bewegt

Betrachten Sie nun ein Quantum (dh ein „Teilchen“), das sich über einen Streifen oder ein Rohr bewegt. Erstens kann es offensichtlich keine Wellenlänge geben, die größer ist als der Querabstand des Streifens oder der Umfang des Rohrs! Dies ist auf dem Rohr leicht zu erkennen: Mindestens ein Grat (rot) und eine Vertiefung (blau), die entlang des Rohrs passen, wie in Abb. 1 dargestellt. 3. Wenn die Wellenlänge größer als S ist, verbindet sich die Welle nicht mit sich selbst, wie in Abb. 3 gezeigt. 4. Die längste Wellenlänge ist genau S; und der einzige Hohlraum der Welle sollte genau auf der Seite des Rohrs liegen, die dem einzigen Kamm gegenüberliegt.

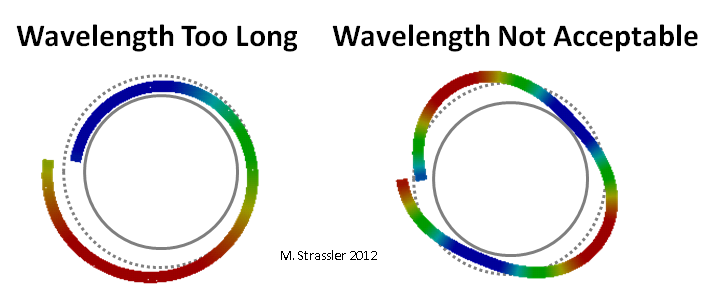Abb. 4: falsche Wellenlängen

Der Kamm und die Mulde der Welle in Abb. 3 bewegen Sie sich um das Rohr herum und ähneln (Abb. 5) einem gewöhnlichen Nicht-Quantenteilchen (hier meine ich wirklich so etwas wie ein Sandkorn, kein Quanten- oder „Teilchen“), das entlang des Rohrs rollt, aber mit einem wichtigen Unterschied: Wenn ein gewöhnliches intuitives Teilchen keine Probleme hat kann sich etwas schneller oder langsamer bewegen, wodurch sein Impuls leicht zunimmt oder abnimmt. Das der Welle entsprechende Quantum kann keinen etwas größeren oder kleineren Impuls haben, da dies einer nicht akzeptablen Wellenlänge entsprechen würde (Abb. 4).

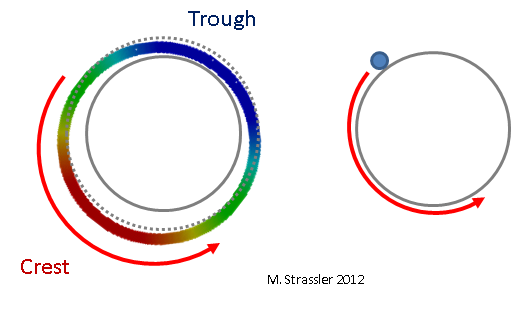Abb. 5: teilchenartige Welle

Auf einem Streifen ist es etwas kniffliger, aber wie in Abb. 6 kann es wiederum nur einen Kamm an einer Wand und einen an der anderen geben, und diese Situation ändert sich im Laufe der Zeit: Der Kamm bewegt sich nicht, sondern nimmt an Größe ab und verwandelt sich in einen Hohlraum, und der Hohlraum verwandelt sich in einen Kamm. Beachten Sie, dass im Gegensatz zu Abb. 3, wo der Kamm und der Graben ihre Größe behalten, sich aber entlang des Rohrs bewegen, bewegt sich der Kamm dieser Welle nicht, sondern zieht sich zusammen. Daher wird es eine "stehende Welle" genannt. Stellen Sie sich für ein ähnliches (aber nicht identisches) Beispiel eine Saite einer Gitarre oder Geige vor. Intuitiv entspricht diese stehende Welle einem gewöhnlichen Nichtquantenteilchen, das sich über einen Streifen vorwärts und rückwärts bewegt. (Weniger intuitiv, aber genauer gesagt, entspricht es einem gewöhnlichen Teilchen, das sich gleichzeitig in beide Richtungen bewegt. Diese sehr seltsame und kühle Quanten Tatsache ist jedoch jetzt unwichtig.) Dies ist in Abb. 1 dargestellt. 7.

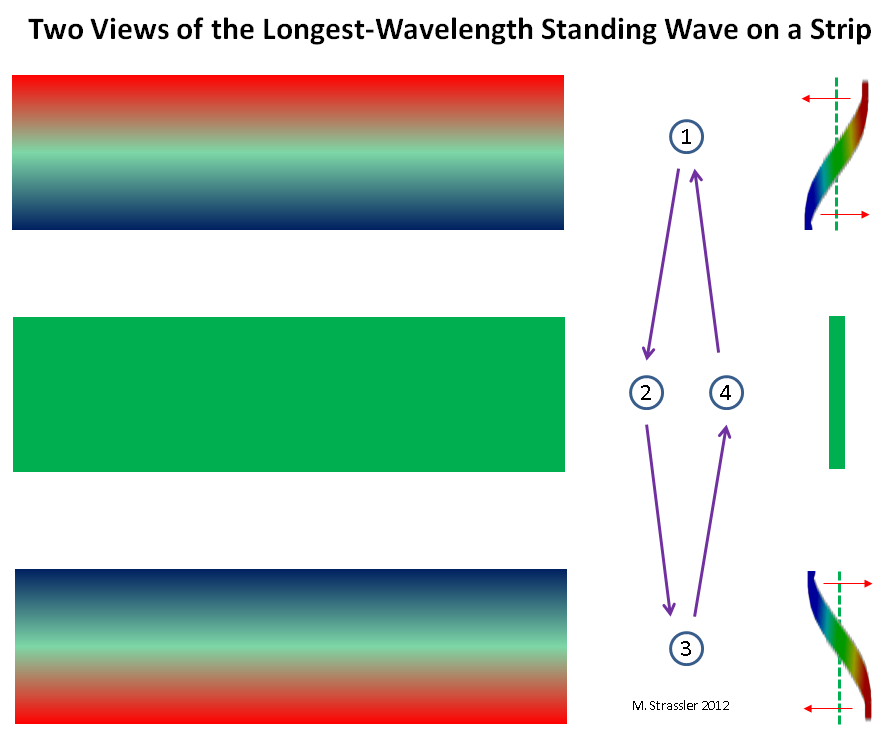Abb. 6: zwei Ansichten der stehenden Welle mit der längsten Wellenlänge

In beiden Fällen gibt es die größtmögliche Wellenlänge (S für Rohr, 2 W für Streifen). Und das bedeutet, dass es den kleinstmöglichen Impuls gibt (h / S und h / 2 W für Rohr und Streifen). Und schließlich bedeutet dies, dass es das einfachstmögliche KK-Partikel gibt! Mit Masse M, wo

M^{2} = m^{2} + (p_{ü b e r} / c)^{2} = m^{2} + (h / c S)^{2} q u a d (R o h r) M^{2} = m^{2} + (p_{ü b e r} / c)^{2} = m^{2} + (h / 2 c W)^{2} q u a d (S t r e i f e n)

$M ^ 2 = m ^ 2 + (p_ {über} / c) ^ 2 = m ^ 2 + (h / c S) ^ 2 \ quad (Rohr) \\ M ^ 2 = m ^ 2 + (p_ { über} / c) ^ 2 = m ^ 2 + (h / 2 c W) ^ 2 \ quad (Streifen)$

Beachten Sie, dass für masselose Partikel, m = 0, diese Formeln reduziert sind auf:

M = h / c S Q u a d (R o h r) M = h / 2 c W Q u a d (S t r e i f e n)

$M = h / c S \ Quad (Rohr) \\ M = h / 2 c W \ Quad (Streifen)$

Und diese letzten Formeln sind ungefähr richtig, wenn S und W sehr klein sind, wie es bei plausiblen Überlegungen häufig der Fall ist.

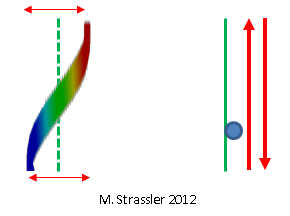Abb. 7: Das Quantum einer stehenden Welle ist ein bisschen wie ein Teilchen, das sich hin und her bewegt

Und so haben wir gelernt, dass die „Teilchen“ tatsächlich Quanten sind, deren Eigenschaften den Eigenschaften von Wellen ähneln:

Im leichtesten KK-Partner ist die Masse M ziemlich viel größer als m,
Da die Formeln für M 1 / W und 1 / S enthalten, ist der leichteste KK-Partner umso schwieriger, je kleiner die zusätzliche Dimension ist.
Wenn S und W so klein werden, dass M m stark überschreitet (oder wenn m anfänglich überhaupt Null ist), ist M ungefähr proportional zu 1 / S oder 1 / W.

Großartig. Dies ist der Hauptpunkt. Vergewissern Sie sich daher, dass Sie ihn verstanden haben, bevor Sie fortfahren. Eine weitere Sache muss noch erklärt werden:

Warum gibt es viele KK-Partner mit unterschiedlichen Massen M, M ', M ”usw. (wobei per Definition M <M '<M ”usw. ist)
Warum sind diese Massen voneinander getrennt?
Warum wachsen Massen mit abnehmender zusätzlicher Dimension?
Warum haben KK-Partner verschiedener Partikeltypen, die sich in derselben zusätzlichen Dimension bewegen können, ähnliche Massen, insbesondere für schwerere KK-Partner?
Warum die Massen von QC-Partnern uns direkte Informationen über Form, Größe und Anzahl zusätzlicher Messungen geben.

Aus den obigen Antworten können ziemlich leicht abgeleitet werden.

Jenseits des leichtesten QC-Partners

Abb. 8: Welle, die der längsten Wellenlänge am nächsten kommt und sich entlang der kurzen Abmessung des Rohrs bewegt

Warum gibt es viele KK-Partner? Nur weil Quantenwellen auf einem Streifen oder einer Röhre viele verschiedene Wellenlängen haben können. In Abb. In den Fig. 8, 9 und 10 sieht man Wellen mit einer Länge von 1/2 oder 1/3 des Maximums, die (nach Einstein und de Broglie) einem Quantum von Doppel- und Dreifachimpulsen in Bezug auf das Minimum entsprechen.

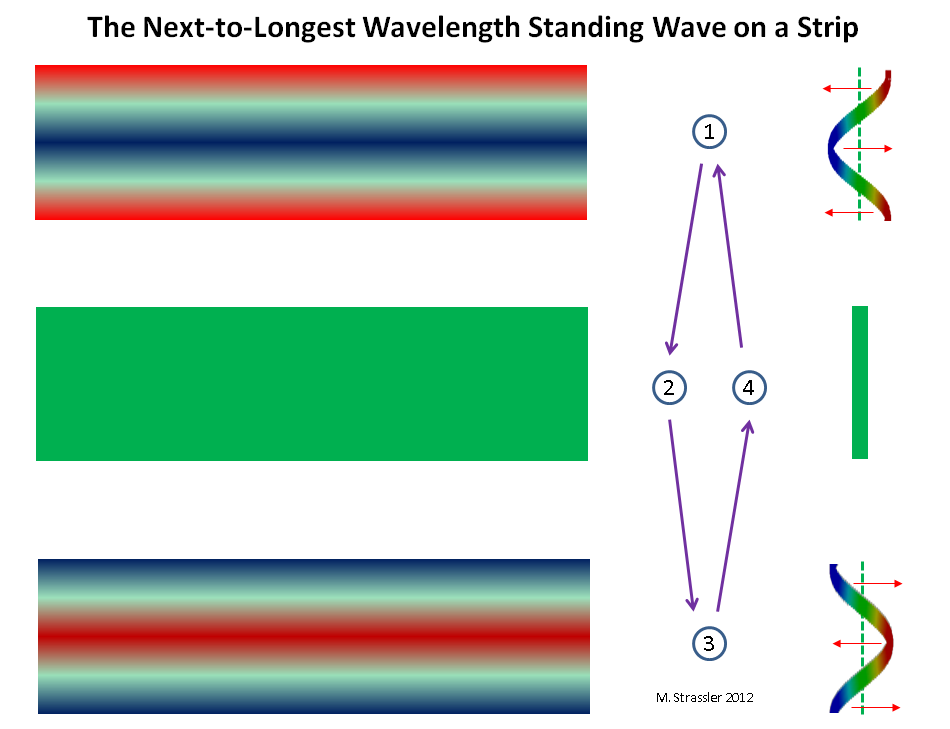Abb. 9 stehende Welle, die der längsten Wellenlänge auf dem Streifen am nächsten liegt

Zusammenfassend können wir sagen, dass jede Wellenlänge zulässig ist, die n Grate und n Täler aufweist, wobei n eine positive ganze Zahl (1, 2, 3, 4, ..) ist, so dass die Wellenlänge gleich S geteilt durch n (oder ist 2W geteilt durch n) und die Welle passen eindeutig in einen Kreis des Kreises S oder in eine Linie der Länge W. Eine andere Wellenlänge ist nicht geeignet (siehe Fig. 4). Dementsprechend ist unter Berücksichtigung der De-Broglie-Beziehung, Impuls = h / Wellenlänge, jeder Impuls der Form nh / S (oder nh / 2 W) zulässig, und für jeden Wert von n haben wir einen KK-Massenpartner:

M^{2} = m^{2} + (p_{ü b e r} / c)^{2} = m^{2} + (n h / c S)^{2} q u a d (R o h r) M^{2} = m^{2} + (p_{ü b e r} / c)^{2} = m^{2} + (n h / 2 c W)^{2} q u a d (S t r e i f e n)

$M ^ 2 = m ^ 2 + (p_ {über} / c) ^ 2 = m ^ 2 + (nh / c S) ^ 2 \ quad (Rohr) \\ M ^ 2 = m ^ 2 + (p_ { über} / c) ^ 2 = m ^ 2 + (nh / 2 c W) ^ 2 \ quad (Streifen)$

Dies beantwortet fast alle gestellten Fragen, zumindest für Fälle mit einer Pfeife und einem Streifen:

Es gibt viele QC-Partner (einer für jedes n> 0),
Ihre Massen sind gut voneinander getrennt (denn wenn sich n um 1 ändert, ändert sich M sehr stark),
Ihre Massen wachsen mit einer Abnahme der zusätzlichen Dimensionen (da die letzten Terme in den Formeln größer werden, wenn W und S kleiner werden),
Schwere KK-Partner unterschiedlicher Teilchen mit unterschiedlichen Massen m haben ähnliche Massen M, da für ausreichend große n die zweiten Terme in den Formeln im Vergleich zu m ² groß sind, was ergibt, dass die Masse des KK-Partners ungefähr gleich M = nh / c S für das Rohr und nh ist / 2 c W für den Streifen, und er ist fast unabhängig von m.

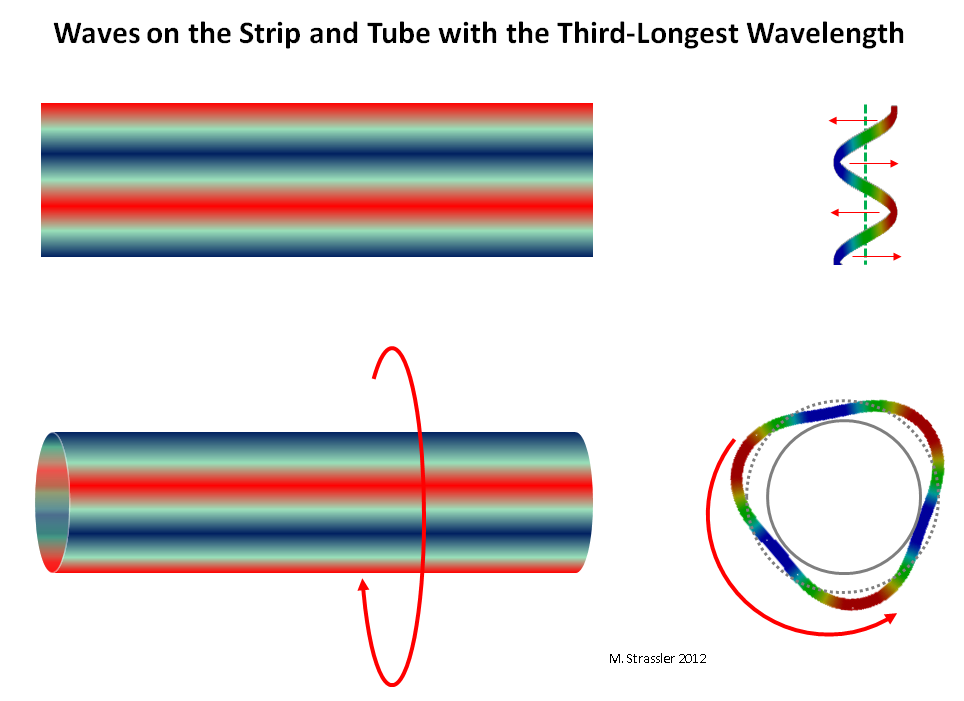Abb. 10: Wellen auf einem Streifen und einem Rohr mit einer Wellenlänge von maximal 1/3

Die letzte Frage bleibt: Warum bestimmen Menge, Größe und Form zusätzlicher Dimensionen die Masse der KK-Partner - und daher können Sie mit der Massenmessung vieler KK-Partner die Eigenschaften zusätzlicher Messungen bestimmen, genau wie Sie mit dem Klang eines Musikinstruments dessen Form grundsätzlich bestimmen können , Größe und Materialien, aus denen es besteht?

Nehmen Sie ein extrem vereinfachtes Beispiel. Wir werden zwei zusätzliche Dimensionen betrachten, die wiederum unseren klassischen Schiffskanal verwenden, einschließlich (wie am Ende eines kürzlich erschienenen Artikels mit Beispielen für zusätzliche Messungen) und der Tatsache, dass der Kanal Tiefe hat, damit wir uns die Wellen darin vorstellen können (Wellen dieses Typs können Sie in einem großen Raum oder unter Wasser in einem beliebigen Kanal hören). Der Abschnitt des Kanals (wenn wir ihn an einem beliebigen Punkt der Linie entlang der langen Dimension schneiden) ist nur ein Rechteck mit der Breite W und der Tiefe D. Wie jedes Nicht-Quantenteilchen kann es sich, auch wenn es unter dem Gesichtspunkt der langen Dimension stationär ist, um ein oder zwei weitere bewegen Messungen (und haben daher einen Impuls entweder in der Breite oder in der Tiefe), und die Welle hat eine Wellenlänge in beiden zusätzlichen Dimensionen. Eine solche einfache Aufteilung der Welle in das, was sie durch Messen der Breite und das Messen durch die Tiefe bewirkt, hängt insbesondere mit der Rechteckigkeit des Kanals zusammen und funktioniert normalerweise in anderen Beispielen nicht. Zum Beispiel, wie in Abb. In 11 hat oben eine der zulässigen Wellen drei Mulden zum Messen der Breite und eine zum Messen der Tiefe.

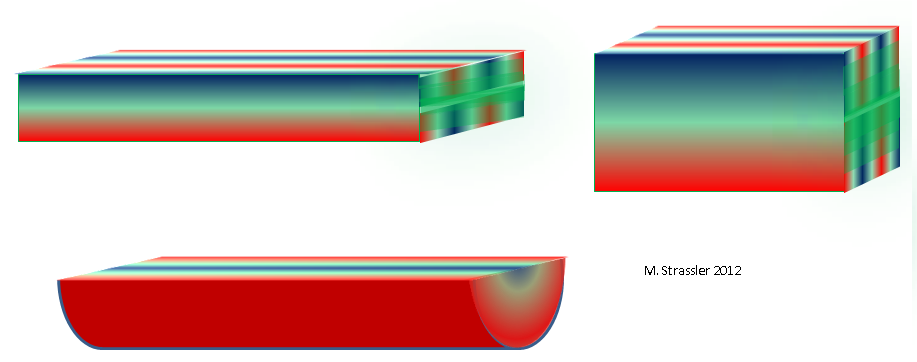Abb. 11

Wir können die Anzahl der Vertiefungen und Grate bestimmen, indem wir die Breite mit der ganzen Zahl n ₁ messen und die Tiefe - n ₂ messen. Für jedes n ₁ und n ₂ (einer oder beide dieser Werte können größer als Null sein) erhalten wir den KK-Partner. Für masselose (m = 0) oder nahezu masselose Quanten haben KK-Partner Masse

M^{2} = m^{2} + (p_{B r e i t e} / c)^{2} + (p_{T i e f e} / c)^{2} = m^{2} + (n_{1} h / 2 c W)^{2} + (n_{2} h / 2 c D)^{2}

$M ^ 2 = m ^ 2 + (p_ {Breite} / c) ^ 2 + (p_ {Tiefe} / c) ^ 2 = m ^ 2 + (n_1 h / 2 c W) ^ 2 + (n_2 h / 2 c D) ^ 2$

Es ist ersichtlich, dass sich die Massenverteilung von dem Fall mit einer zusätzlichen Dimension unterscheidet und dass sie uns sowohl W als auch D sagen kann.

Wenn der Querschnitt des Kanals eine andere Form hat, beispielsweise eine dreieckige oder halbe Scheibe, wie in Fig. 1 gezeigt. In 11 unten erhalten wir eine weitere Massenverteilung, die die genaue Form eines Dreiecks oder einer Halbscheibe widerspiegelt. Und wir können bereits die praktischen Schiffskanäle verwerfen und den dreidimensionalen Raum darstellen, dessen Querschnitt jeder anderen endlichen zweidimensionalen Form entspricht, von denen eine in Abb. 1 dargestellt ist. 1 in einem Artikel über Welten mit zwei räumlichen Dimensionen: eine volle Scheibe oder sogar eine Kugel oder ein Torus. Jedes dieser Formulare gibt uns eine eigene Art der Massenverteilung von QC-Partnern. Und wenn es drei, vier oder fünf zusätzliche Dimensionen geben wird ... Vielleicht viel mehr Arten von Verteilungen.

Beispiele für einige Verteilungen für masselose Partikel mit Größen zusätzlicher Messungen, die so gewählt wurden, dass die Massen der ersten KK-Partner für jeden Fall gleich sind, sind in Abb. 1 angegeben. 12. Es ist offensichtlich, dass es zur Bestimmung der Form und Größe zusätzlicher Messungen erforderlich ist, die Massen einer ausreichend großen Anzahl von KK-Partnern zu messen (und sogar zumindest zu bestätigen, dass eines der neu entdeckten schweren Partikel im Allgemeinen KK-Partner sind), um die Art zusätzlicher Messungen zu verstehen Messungen wird die Zeit vergehen.

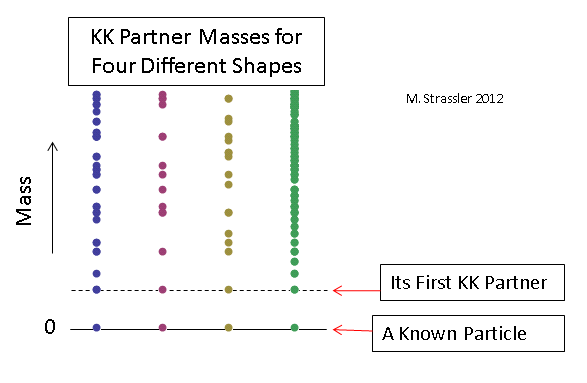Abb. 12

Aber können bekannte schwere Materieteilchen KK-Partner von leichteren sein?

Dann stellt sich die offensichtliche zusätzliche Frage.Wir wissen, dass es unter den bekannten Elementarteilchen ein Elektron sowie seine schwereren Versionen gibt: Myon und Tau. Es gibt einen oberen Quark und seine schwereren Versionen sind verzaubert und wahr. Es gibt einen unteren Quark und seine schwereren Versionen, seltsam und charmant. Sind schwere Partikelversionen die QC-Partner der Lunge?

Auf den ersten Blick ist dies eine verlockende Annahme, aber die Antwort darauf wird ein klares Nein sein. Entschuldigung.Dies ist keine dumme Frage. Es hat nur eine kluge negative Antwort.

Myon und Tau, verzaubert und wahr, seltsam und charmant - sie alle erhalten ihre Masse dank des Higgs-Feldes und nicht dank des Impulses aus zusätzlichen Dimensionen. Dies ergibt sich eindeutig aus detaillierten Experimenten. Tipps finden Sie im Artikel darüber, was passieren würde, wenn das Higgs-Feld Null wäre . Bitte beachten Sie, dass wenn das Higgs-Feld im Durchschnitt Null wäre, das Elektron, das Myon und das Tau keine Masse haben würden (und jedes in zwei Arten von Partikeln unterteilt wäre). Dies entspricht nicht der Theorie, dass Myon und Tau KK-Partner des Elektrons sind.

Es gibt viele andere Gründe. Die schwerwiegendste davon wird vielleicht sein, dass sich das Photon aufgrund des Vorhandenseins einer Ladung auf dem Elektron und der Tatsache, dass es von einem elektrischen Feld umgeben ist, in jeder Dimension bewegen muss, in der sich das Elektron bewegt (obwohl das Gegenteil nicht der Fall ist). Wenn das Elektron also KK-Partner hat, sollte das Photon diese auch haben. Aus unseren Formeln (und allgemeineren, die ihnen ähnlich sind) folgt jedoch, dass das Photon keine Masse hat und die Elektronenmasse (0,0005 GeV / c ² ) im Vergleich zur Myonenmasse (etwa 0,1 GeV / c ² ) klein ist) Wenn das Myon ein KK-Partner ist, muss das Photon einen KK-Partner mit ähnlicher Masse haben. Aber ein solches Teilchen wäre, wenn es existiert hätte, vor vielen Jahren entdeckt worden. Tatsächlich wurden KK-Partner von Photonen in Experimenten nicht beobachtet, in denen Massen untersucht wurden, die viel größer als die Masse von Z-Teilchen waren - dies sind viele hundert GeV / s ² . Das Z-Teilchen selbst kann auch kein QC-Partner eines Photons sein; sie sieht ihm nicht genug ähnlich Und das bedeutet, dass alle KK-Partner des Elektrons mindestens so schwer sein sollten.

Wohin als nächstes? Zu Experimenten

Wir gingen von der Theorie (die Möglichkeit zusätzlicher Messungen, verwandter Mathematik und Geometrie) zu Vorhersagen (QC-Partner) über. Nächster Schritt: Was wissen wir über zusätzliche Messungen aus Experimenten? Wir haben noch keine KK-Partner in den Experimenten gesehen, aber wir fragen uns vielleicht, was wir aus ihrer Abwesenheit lernen können. Sehr viel, wie ich später erläutern werde, zusammen mit einer Beschreibung, wie Versuche, Anzeichen für zusätzliche Messungen zu finden, am Large Hadron Collider und anderswo fortgesetzt werden.