Ist unser Universum unendlich?
Achtung! In diesem Artikel wird nur eine Theorie ohne wissenschaftliche Beweise ausgedrückt.
Guten Tag Giktayms! Ich wurde von einem YouTube-Video über ungewöhnliche numerische Paradoxien dazu gedrängt, diesen Artikel zu schreiben. Das heißt, die Paradoxien von
Zeno und warum es unmöglich ist, durch Null zu teilen, die heute diskutiert werden.
Zenos Paradoxon lässt sich sehr leicht anhand von
Achilles und der Schildkröte erklären. Diejenigen, die mit diesem Paradox nicht vertraut sind, hier ist ein visuelles Video eines anderen Autors:
Ich empfehle Ihnen, vor dem weiteren Lesen zu lesen. (Achilles Paradoxon und Schildkröten)
(Achilles Paradoxon und Schildkröten)Wenn Sie das Video nicht sehen möchten, werde ich Ihnen kurz sagen: Stellen Sie sich vor, Achilles rennt einer Schildkröte hinterher, die ihn überholt. Der Abstand zwischen ihnen nimmt ständig ab, da Achilles schneller läuft als eine Schildkröte. Wenn sich Achilles einer Entfernung von 1 Meter nähert, entspricht dies nach einer Weile
0,1 Metern, dann
0,01 usw. bis unendlich. Dies bedeutet, dass Achilles die Schildkröte niemals einholen wird, aber in Wirklichkeit ist alles völlig falsch.
In Wirklichkeit gibt es kein Problem, wir nehmen Achilles und die Schildkröte, stellen sie auf ein Laufband und bitte, Achilles überholt die Schildkröte ruhig. Genau darin liegt der mögliche Beweis, dass das Universum nicht unendlich ist.
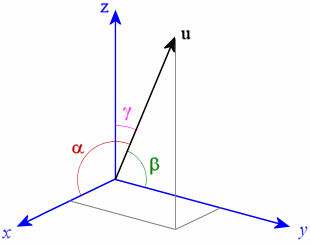 (Vektor im 3D-Raum)
(Vektor im 3D-Raum)Versuchen wir dies anhand des Prinzips der Computerspiele zu erklären. Typischerweise wird die Position eines Objekts als Vektor geschrieben, der aus den x-, y- und z-Achsen besteht. Und jeder Wert wird im Datentyp
float (Gleitkommawert) gespeichert. Beispielsweise verwendet
Unity3D einen 32-Bit-Float, um seine Position im Raum anzuzeigen. Der Mindestwert davon:
1.175494351 E - 38. Dies ergibt eine gleichmäßige Bewegung in nahezu jeder Skala. Hier ist das wichtige Wort
„fast“ , dh wenn wir das Modell stark reduzieren und approximieren, werden wir sehen, wie es sich in Sprüngen bewegt. Springen von
0, ... 1 nach
0, ... 2 nach
0, ... 3 usw. Dies bedeutet, dass Achilles in der Simulation in jedem Szenario die Schildkröte überholt. Aber wie sie sagen, gibt es kein Böses ohne Gutes. Wenn wir einen minimalen Float-Wert haben, gibt es sozusagen einen maximalen Rand des
3D- Raums. Darüber hinaus werden wir
die Gesetze der Physik der virtuellen Welt nicht zulassen
(nennen wir
es) . In Wirklichkeit können wir einfach nicht mehr als den Maximalwert einer Variablen angeben.
Wenn wir zum Paradoxon von Zeno zurückkehren, wird Achilles die Schildkröte nicht nur nie einholen, sondern niemals die Grenze seiner Fantasiewelt erreichen, für ihn wird es unendlich sein. Von -∞ bis + ∞ erhalten wir seltsamerweise die gleiche Funktion
f (x) = 1 / x . Und das Lustigste ist, dass der
x / 0- Wert nicht in diese Funktion fällt, da die Funktion niemals Null erreichen wird, wie Achilles die Schildkröte.
(Eigentlich kann dies nicht durch Null geteilt werden)Genug Theorie, lasst uns üben. Nehmen wir die reale Welt, wir bestehen alle aus Atomen, Atome bestehen aus Neutronenprotonen und Elektronen, die wiederum aus Quarks
(Elementarteilchen) bestehen . Sowohl in der Simulation als auch in der realen Welt muss Achilles keine Schildkröte überholen. All dies führt dazu, dass sowohl in der Simulation als auch in der Realität Elementarteilchen um die Zahlen
0, ... 1 0, ... 2 0, ... 3 springen müssen
, wie dies im Spiel geschieht, da Achilles überholen kann Schildkröte hier und da. Dies sagt uns, dass das Zeno-Paradoxon nur auf Papier oder in seinem Koordinatensystem funktioniert, dessen Wert von -∞ bis + ∞ liegt. In Wirklichkeit überholen die Elementarteilchen von Achilles beim Springen auf die kleinsten Werte irgendwann die Schildkröte, ihre Koordinaten werden gleich, wonach Achilles vorwärts rennt.
Nachdem wir gelernt haben, welches Koordinatensystem unser Raum verwendet, kehren wir zum Hauptthema zurück. Wenn wir einen Minimalwert haben, gibt es einen Maximalwert - den
Rand unseres Universums . Es gibt diejenigen, die sagen werden, warum es dann einerseits unendlich und andererseits endlich sein kann. Das Problem ist jedoch, dass die Koordinaten oder die Position nur ein Element eines großen Systems sind, das als Raum bezeichnet wird, und dass es entweder vollständig unendlich oder vollständig endlich sein kann. Dies alles wirft auch die Frage auf, und zufällig befinden wir uns nicht in einer Computersimulation, oder? Dies ist jedoch ein Thema für einen anderen Artikel.
Zusammenfassung
So sind wir heute zu dem Schluss gekommen, dass das Universum
NICHT unendlich ist. In diesem Beitrag wurde nur die Theorie ausgedrückt, wie niemand das Universum dort wirklich kennt und es nicht beweisen kann. Aber vielleicht habe ich mit diesem Artikel jemanden dazu gedrängt, neue Entdeckungen zu machen.
Quelle