Die Navier-Stokes-Gleichungen beschreiben einfache Alltagsphänomene wie das aus einem Gartenschlauch fließende Wasser. Sie basieren jedoch auf einem Problem, dessen Lösung auf eine Million Dollar geschätzt wurde

In der Physik gibt es Gleichungen, die alles von der Raumzeit bis zum Flug eines Photons beschreiben. Nur ein Satz von Gleichungen wird jedoch als so mathematisch komplex angesehen, dass er als eines der sieben "
Millenniumsprobleme " ausgewählt wurde, für die das
Clay Institute of Mathematics einen Preis von einer Million Dollar anbietet: Dies sind
die Navier-Stokes-Gleichungen , die den Flüssigkeitsfluss beschreiben.
Kürzlich schrieb ich darüber, wie ein wichtiges neues Ergebnis für diese Gleichungen erhalten wurde. Und diese Arbeit zeigt, dass die Fortschritte auf dem Weg zum Millenniumspreis schwieriger sein werden als erwartet. Warum sind diese Gleichungen, die so bekannte Phänomene wie das durch einen Schlauch fließende Wasser beschreiben, mathematisch schwieriger zu verstehen als beispielsweise die Einstein-Feldgleichungen, die so atemberaubende Objekte wie Schwarze Löcher enthalten?
Die Antwort liegt, wie ich es verstehe, in Turbulenzen. Wir alle haben dieses Phänomen im Flug in inhomogener Luft in 10.000 m Höhe oder bei der Beobachtung eines Trichters aus dem Wasser erlebt, der den Abfluss im Bad verlässt. Wissen folgt jedoch nicht aus dem Bewusstsein: Turbulenzen sind einer der am wenigsten verstandenen Bereiche der physischen Welt.
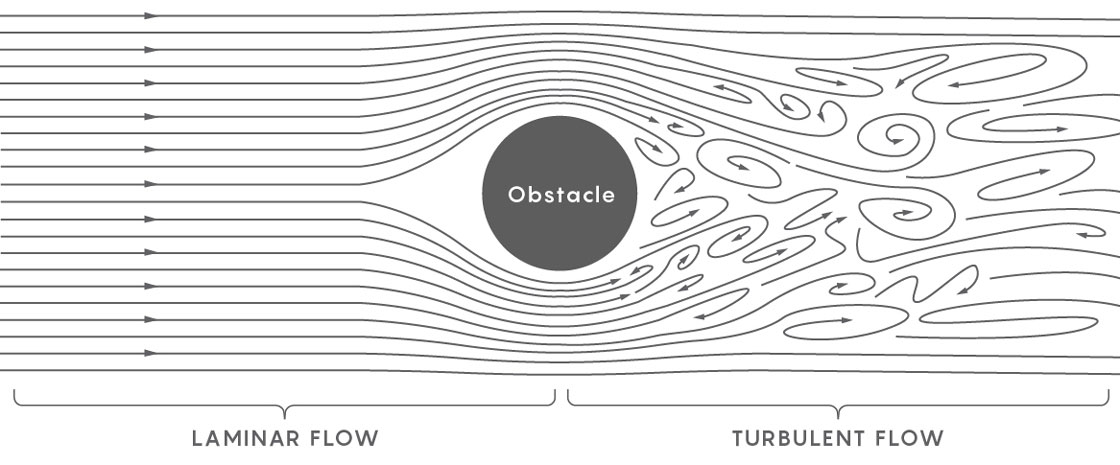
Ein Beispiel für eine Strömung ohne Turbulenzen ist ein ruhiger Fluss. Jeder Teil davon bewegt sich mit der gleichen Geschwindigkeit in die gleiche Richtung. Turbulente Flüssigkeit tritt auf, wenn der Strom eines Flusses bricht, sodass sich verschiedene Teile des Flusses mit unterschiedlichen Geschwindigkeiten in verschiedene Richtungen bewegen. Physiker beschreiben die Bildung von Turbulenzen zunächst als das Auftreten eines Trichters in einer gleichmäßigen Strömung und dann als die Bildung kleiner Trichter im ersten Trichter und noch kleinerer Trichter in diesen Trichtern - ein Meer von Trichtern, die in die Flüssigkeit gelangen, so dass die Flüssigkeit in einzelne Teile zerfällt, von denen jeder interagiert miteinander und bewegt sich in seine eigene Richtung.
Die Forscher wollen genau verstehen, wie eine gleichmäßige Strömung in turbulente Turbulenzen zerfällt, und die zukünftige Form des Fluids modellieren, nachdem die Turbulenzen ihren Tribut gefordert haben. Die Millennium Challenge ist jedoch bescheidener formuliert: Sie müssen nur beweisen, dass es immer Lösungen gibt. Das heißt, die Frage ist, können Gleichungen jede Flüssigkeit mit beliebigen Anfangsbedingungen und einer unendlich fernen Zukunft beschreiben?
"Der erste Schritt besteht einfach darin, zu beweisen, dass die Gleichungen einige Lösungen haben", sagt Charlie Fefferman, Mathematiker an der Princeton University. "Dies gibt kein wirkliches Verständnis für das Verhalten von Flüssigkeiten, aber wenn Sie dies auch nicht haben, wissen Sie nichts."
Wie kann man also die Existenz von Lösungen beweisen? Sie müssen zunächst verstehen, warum dies möglicherweise nicht der Fall ist. Die Navier-Stokes-Gleichungen implizieren die Berechnung von Änderungen solcher Größen wie Geschwindigkeit und Druck. Mathematiker sind besorgt über das folgende Szenario: Sie laufen diese Gleichungen weg und nach einiger Zeit sagen sie Ihnen, dass sich ein flüssiges Teilchen mit unendlicher Geschwindigkeit bewegt. Und das ist das Problem - die Änderung des unendlichen Wertes zu berechnen ist nicht einfacher als durch Null zu teilen. Mathematiker nennen solche Situationen eine „Explosion“, und im Falle einer Explosion funktionieren die Gleichungen nicht mehr und es werden keine Lösungen gefunden.
 Die Navier-Stokes-Gleichungen beschreiben den Fluss einer inkompressiblen Flüssigkeit.
Die Navier-Stokes-Gleichungen beschreiben den Fluss einer inkompressiblen Flüssigkeit.
Im Allgemeinen entspricht das Produkt aus Masse (blauer Teil) und Beschleunigung (violett) den auf die Flüssigkeit einwirkenden Kräften (orange):- ρ ist die Flüssigkeitsdichte;
- dV / dt - Geschwindigkeitsänderung im Laufe der Zeit;
- V ∇V - Geschwindigkeit und Bewegungsrichtung;
- ∇P - Änderung des Innendrucks;
- ρ g - der Einfluss äußerer Kräfte (zum Beispiel der Schwerkraft);
- μ ∇ 2 V - der Einfluss von Schnittgrößen (Viskosität).
Der Beweis für das Fehlen von Explosionen (und das Vorhandensein von Lösungen) entspricht dem Beweis, dass die maximale Geschwindigkeit eines flüssigen Partikels durch einen endlichen Wert begrenzt bleibt. Eine der wichtigsten Größen ist die kinetische Energie der Flüssigkeit.
Wenn Sie beginnen, den Fluss mithilfe der Navier-Stokes-Gleichungen zu simulieren, verfügt Ihre Flüssigkeit über eine anfängliche Energiemenge. In turbulenten Strömungen kann sich Energie konzentrieren. Anstatt sich gleichmäßig im Fluss auszubreiten, kann kinetische Energie in Whirlpools beliebig kleiner Größe gesammelt werden, und Partikel in diesen Whirlpools können (theoretisch) auf unendliche Geschwindigkeit beschleunigen.
„Mit dem Übergang zu immer kleineren Maßstäben wird die kinetische Energie für die Entscheidungskontrolle immer weniger nützlich. Die Entscheidung kann alles und ich weiß nicht, wie ich sie kontrollieren soll “, sagt Vlad Vikol, Mathematiker an der Princeton University, der eine neue Arbeit mit Tristan Buckmaster geschrieben hat.
Mathematiker klassifizieren teilweise Differentialgleichungen anhand des Ausmaßes, in dem sie sich auf unendlich kleinen Skalen schlecht verhalten können. Die Navier-Stokes-Gleichungen befinden sich am äußersten Ende dieser Skala. Die Komplexität der Gleichungsmathematik spiegelt gewissermaßen die Komplexität der turbulenten Strömungen wider, die sie beschreiben müssen.
„Wenn Sie eine Stelle vergrößern, verlieren Sie aus mathematischer Sicht Informationen über die Lösung“, sagt Vikol. "Aber Turbulenzen sollten genau das beschreiben - die Übertragung von kinetischer Energie von großen auf immer kleinere Maßstäbe. Sie müssen also wirklich vergrößern."

Wenn wir über die mathematischen Eigenschaften physikalischer Gleichungen sprechen, ist es natürlich, eine Frage zu stellen: Werden diese Argumente die Art und Weise verändern, wie wir die physikalische Welt betrachten? Im Fall der Navier-Stokes-Gleichungen und des Millennium-Problems lautet die Antwort sowohl "Ja" als auch "Nein". Nach fast 200 Jahren des Experimentierens ist klar, dass die Gleichungen funktionieren: Der von Navier-Stokes vorhergesagte Fluss stimmt nacheinander mit dem in den Experimenten beobachteten Fluss überein. Wenn Sie ein Physiker sind, der in einem Labor arbeitet, kann dies für Sie ausreichen. Aber Mathematiker müssen mehr wissen - sie möchten prüfen, ob es möglich ist, diese Gleichungen vollständig zu befolgen, um zu überwachen, wie genau sich die Strömung von einem Moment zum anderen ändert (für jede anfängliche Fluidkonfiguration), und sogar um die Turbulenzquelle zu erfassen.
„Das Verhalten von Flüssigkeiten ist voller Überraschungen“, sagt Fefferman. "Diese Überraschungen werden im Prinzip durch die grundlegenden Gleichungen erklärt, die den Flüssigkeitsfluss steuern. Es ist jedoch ein Rätsel, wie man von den Gleichungen, die die Bewegung einer Flüssigkeit steuern, zu einer Beschreibung der tatsächlichen Bewegung der Flüssigkeit übergeht."