Zwei Mathematiker haben bewiesen, dass die Navier-Stokes-Gleichungen unter bestimmten extremen Bedingungen Unsinn ergeben
Die Navier-Stokes-Gleichungen beschreiben mit Hilfe mehrerer lakonischer Begriffe eines der häufigsten Phänomene der physikalischen Welt: den Flüssigkeitsfluss. Heute werden diese Gleichungen aus den 1820er Jahren verwendet, um alles zu beschreiben, von Meeresströmungen und Turbulenzen nach einem Flugzeug bis zum Blutfluss ins Herz.
Obwohl Physiker diese Gleichungen wie einen Hammer für zuverlässig halten, misstrauen Mathematiker ihnen. Für einen Mathematiker bedeutet die Tatsache, dass diese Gleichungen zu funktionieren scheinen, nicht viel. Sie brauchen den Beweis, dass die Gleichungen fehlerfrei sind: Für jede Flüssigkeit und für die Langzeitprognose, die bis in die Zukunft verteilt ist, wird die Mathematik der Gleichungen nicht versagen. Es war nicht einfach, eine solche Garantie zu finden. Die erste Person oder das erste Team, die bzw. das nachweisen kann, dass die Navier-Stokes-Gleichungen immer funktionieren - oder ein Beispiel dafür liefert, dass sie nicht funktionieren -, kann eine Belohnung für die Lösung eines der vom
Clay's Mathematical Institute angekündigten
Millennium-Probleme und eine Million Dollar erhalten zusätzlich [ab 2017 wurde nur eine der sieben Aufgaben des Jahrtausends (Poincaré-Hypothese) von Gregory Perelman / ca. gelöst. übersetzt.].
Mathematiker haben viele Möglichkeiten entwickelt, um dieses Problem zu lösen. Die neue Arbeit, die im September veröffentlicht wurde, wirft ernsthafte Fragen auf, ob einer der beliebtesten Ansätze für das über viele Jahre entwickelte Problem erfolgreich sein kann. Die Arbeit von Tristan Buckmaster und Vlad Vikol von der Princeton University ist das erste Ergebnis, das zeigt, wie die Navier-Stokes-Gleichungen unter bestimmten Bedingungen eine widersprüchliche Beschreibung der physischen Welt liefern.
"Wir versuchen, bestimmte Probleme zu verstehen, die diesen Gleichungen inhärent sind, und warum die Leute sie wahrscheinlich überdenken müssen", sagt Buckmaster.
Die Arbeit von Buckmaster und Wikol zeigt, dass wenn Sie beim Lösen der Navier-Stokes-Gleichungen sehr grobe Annahmen treffen, diese keinen Sinn ergeben: Sie sagen, dass dieselbe Flüssigkeit mit denselben Anfangsbedingungen in zwei oder mehr verschiedenen Zuständen auftreten kann. Es kann auf eine oder eine ganz andere Weise fließen. Wenn ja, können diese Gleichungen die physikalische Welt, für die sie entwickelt wurden, nicht zuverlässig beschreiben.
Explodierende Gleichungen
Um zu verstehen, wie Gleichungen brechen können, stellen Sie sich eine Meeresströmung vor. Innerhalb seines Rahmens können lokale Flüsse existieren, wodurch sich einige seiner Teile in eine Richtung und mit einer Geschwindigkeit und andere in eine andere Richtung mit einer anderen Geschwindigkeit bewegen können. Lokale Strömungen interagieren miteinander in ständiger gegenseitiger Wirkung von Reibung und Wasserdruck, die ihre Strömung bestimmen.
Mathematiker modellieren diese Interaktion mithilfe einer Karte, die Sie über die Richtungen und Durchflussraten an jedem Punkt in der Flüssigkeit informiert. Diese als Vektorfeld bezeichnete Karte ist eine Momentaufnahme der internen Dynamik einer Flüssigkeit. Die Navier-Stokes-Gleichungen nehmen dieses Bild auf und reproduzieren es als Video, wobei angegeben wird, wie genau das Vektorfeld zu jedem nachfolgenden Zeitpunkt aussehen wird.
Die Windkarte (windy.com) funktioniert ähnlich wie ein Vektorfeld. An jedem Punkt hat der Wind eine bestimmte Richtung und Stärke.Diese Gleichungen funktionieren. Sie beschreiben den Flüssigkeitsfluss so zuverlässig, wie Newtons Gleichungen die zukünftigen Positionen der Planeten vorhersagen. Physiker verwenden sie ständig und sie stimmen ständig mit den Ergebnissen von Experimenten überein. Mathematiker brauchen jedoch mehr als eine episodische Bestätigung - sie brauchen den Beweis, dass die Gleichungen nicht verletzt werden, dass die Gleichungen Ihnen immer geben, egal von welchem Vektorfeld Sie ausgehen und wie weit Sie es in Zukunft reproduzieren neues, einzigartiges Vektorfeld.
Dies ist das Thema des Millennium-Problems, bei dem gefragt wird, ob die Navier-Stokes-Gleichungen für alle Startpunkte zu allen Zeitpunkten Lösungen haben (die Lösung ist tatsächlich ein Vektorfeld). Diese Lösungen sollten die genaue Richtung und Stärke des Durchflusses an jedem Punkt in der Flüssigkeit sicherstellen. Lösungen, die Informationen mit einer so unendlich kleinen Auflösung liefern, werden als "glatt" bezeichnet. Für eine reibungslose Lösung ist jedem Punkt des Feldes ein Vektor zugeordnet, mit dem Sie sich "reibungslos" um das Feld bewegen können, ohne an Punkten hängen zu bleiben, an denen der Vektor fehlt - an einem Punkt, an dem Sie die weitere Bewegung nicht verstehen.
Glatte Lösungen sind eine vollständige Darstellung der physischen Welt, aber aus mathematischer Sicht existieren sie möglicherweise nicht immer. Mathematiker, die an Gleichungen wie diesen arbeiten, sorgen sich um diese Situation: Sie führen die Navier-Stokes-Gleichungen aus und beobachten die Änderungen im Vektorfeld. Nach einer begrenzten Zeit sagen Ihnen die Gleichungen, dass sich ein bestimmtes Flüssigkeitsteilchen mit unendlicher Geschwindigkeit bewegt. Dann werden Sie Probleme haben. Die Gleichungen umfassen das Messen von Änderungen von Eigenschaften wie Druck, Reibung und Flüssigkeitsgeschwindigkeit - im Jargon sprechen sie Ableitungen dieser Größen -, aber es ist nicht einfacher, die Ableitung einer unendlichen Größe zu nehmen, als durch Null zu teilen. Wenn die Gleichungen also einen unendlichen Wert ergeben, können wir sagen, dass sie Sie abgelehnt haben oder „explodiert“ sind. Sie können die nachfolgenden Zustände Ihrer Flüssigkeit nicht mehr beschreiben.
Eine solche „Explosion“ ist ein Beweis dafür, dass den Gleichungen eine Beschreibung einiger Eigenschaften der physikalischen Welt fehlt, die sie beschreiben müssen. „Vielleicht decken die Gleichungen nicht alle Auswirkungen einer realen Flüssigkeit ab, weil wir in einer realen Flüssigkeit keine unendliche Teilchengeschwindigkeit erwarten“, sagt Buckmaster.
Die Lösung für das Millennium-Problem besteht entweder darin, zu zeigen, dass die Navier-Stokes-Gleichungen niemals explodieren, oder die Bedingungen zu finden, unter denen dies geschieht. Eine der von Mathematikern verwendeten Strategien besteht darin, die Anforderungen zu mildern, wie genau diese Gleichungen die erforderlichen Lösungen beschreiben sollen.
Strömungsstörung
Die Navier-Stokes-Gleichungen müssen den Fluss einer Flüssigkeit unter beliebigen Anfangsbedingungen beschreiben und die Beschreibung unendlich weit in die Zukunft erweitern. Um diese Fähigkeit zu beweisen, „schwächen“ Mathematiker manchmal, dh sie verwenden ungefähre Beschreibungen von Vektorfeldern, die eine Flüssigkeit beschreiben. Aber es gibt Schwierigkeiten damit.
Im Idealfall möchten Mathematiker beweisen, dass die Anwendung der Navier-Stokes-Gleichungen auf eine kontinuierliche, „glatte“ Flüssigkeit ein einzigartiges Ergebnis liefert.
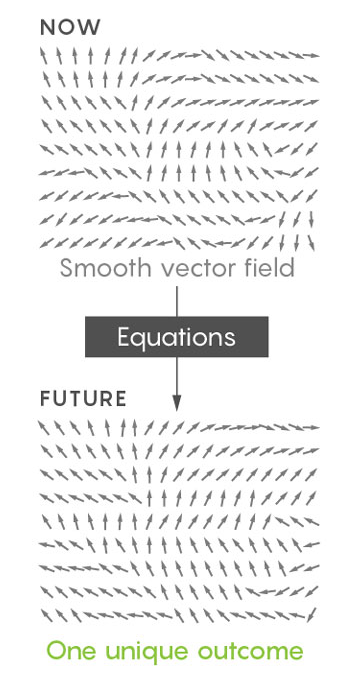
Es ist jedoch einfacher, mit "schwachen", nicht so detaillierten Vektorfeldern zu arbeiten. Und Mathematiker haben herausgefunden, dass einige schwache Beschreibungen nicht eindeutige Ergebnisse liefern - sie lassen dieselbe Flüssigkeit auf zwei Arten unter denselben Anfangsbedingungen fließen.
Von schwach bis glatt
Wenn Mathematiker solche Gleichungen studieren, beginnen sie manchmal, die Definition dessen, was eine Lösung darstellt, zu erweitern. Glatte Lösungen erfordern maximale Informationen - im Fall von Navier-Stokes müssen an jedem Punkt im Vektorfeld, der der Flüssigkeit zugeordnet ist, ein Vektor vorhanden sein. Was aber, wenn wir die Anforderungen lockern und sagen, dass Sie Vektoren nur für einige Punkte des Feldes berechnen müssen oder nur ungefähre Werte der Vektoren erhalten müssen? Solche Entscheidungen werden als "schwach" bezeichnet. Sie ermöglichen es Mathematikern, das Verhalten der Gleichung zu spüren, ohne die mühsame Aufgabe, absolut alle Lösungen zu finden (was in der Praxis möglicherweise nicht möglich ist).
Tristan Buckmaster, Mathematiker an der Princeton University"Unter bestimmten Gesichtspunkten sind schwache Entscheidungen noch einfacher zu beschreiben als echte, weil man viel weniger wissen muss", sagte Camillo De Lellis, gemeinsam mit Lazlo Schekelikhidi verfasst, der mehrere wichtige Werke schrieb, die den Grundstein für die Arbeit von Buckmaster und Vikola legten.
Schwache Lösungen gibt es in verschiedenen Qualitäten. Wenn Sie sich eine reibungslose Lösung in Form eines mathematischen Bildes einer Flüssigkeit mit unendlicher Auflösung vorstellen, sind schwache Lösungen etwa 32-Bit-, 16-Bit- oder 8-Bit-Versionen dieses Bildes.
1934 definierte der französische Mathematiker
Jean Leray eine wichtige Klasse schwacher Lösungen. Anstatt mit exakten Vektoren zu arbeiten, nehmen die „Leray-Lösungen“ den Durchschnittswert der Vektoren in einer kleinen Nachbarschaft des Vektorfeldes. Leray hat bewiesen, dass Sie die Navier-Stokes-Gleichungen immer lösen können, sodass Ihre Entscheidungen die Form dieser Art annehmen können. Mit anderen Worten, Leras Entscheidungen explodieren nicht.
Die Leistung von Lera bestimmte eine neue Herangehensweise an das Navier-Stokes-Problem: Beginnen Sie mit Leras Lösungen, deren Existenz bereits bekannt ist, und prüfen Sie, ob sie in reibungslose Lösungen umgewandelt werden können, deren Existenz Sie beweisen möchten. Dieser Vorgang ähnelt dem, bei dem Sie mit einem groben Bild beginnen und prüfen, ob Sie die Auflösung schrittweise drehen können, um das perfekte Bild der Realität zu erhalten.
"Eine der möglichen Strategien besteht darin, zu zeigen, dass diese schwachen Lera-Entscheidungen reibungslos sind. Wenn Sie zeigen können, dass sie reibungslos sind, lösen Sie die Millennium-Herausforderung", sagte Bakmaster.
Vlad Vkol repräsentiert die Hälfte des Teams, das Probleme bei der Überprüfung der Navier-Stokes-Gleichungen aufgedeckt hat.Es gibt noch einen weiteren Haken. Die Lösungen der Navier-Stokes-Gleichungen entsprechen realen physikalischen Ereignissen, und physikalische Ereignisse treten auf eine mögliche Weise auf. Vor diesem Hintergrund möchte ich, dass Ihre Gleichungen nur einen Satz einzigartiger Lösungen haben. Wenn die Gleichungen Ihnen viele mögliche Lösungen bieten, können sie ihre Arbeit nicht erledigen.
Daher können Mathematiker Lerays Lösungen nur dann zur Lösung der Millenniumsprobleme verwenden, wenn Lerays Lösungen einzigartig sind. Nicht eindeutige Leray-Lösungen bedeuten, dass gemäß den Navier-Stokes-Regeln dieselbe Flüssigkeit mit denselben Anfangsbedingungen zu zwei verschiedenen physikalischen Zuständen kommen kann, die keine physikalische Bedeutung haben, und impliziert, dass die Gleichungen nicht tatsächlich beschreiben was soll.
Das neue Ergebnis von Bakmaster und Wikol ist der erste Hinweis darauf, dass dies bei bestimmten Definitionen schwacher Entscheidungen passieren kann.
Viele Welten
In ihrer neuen Arbeit betrachten Buckmaster und Wikol noch schwächere Lösungen als die Lösungen von Leray - Lösungen, die das gleiche Mittelungsprinzip wie die von Leray verwenden, aber eine weitere Anforderung schwächen (bekannt als Energieungleichheit). Sie verwenden die Methode der „konvexen Integration“, die aus der Arbeit an der Geometrie des Mathematikers John Nash stammt und später von De Lellis und Schekelikhidi an der Untersuchung von Flüssigkeiten beteiligt ist.
Mit diesem Ansatz beweisen Buckmaster und Wikol, dass diese sehr schwachen Lösungen der Navier-Stokes-Gleichungen nicht eindeutig sind. Sie zeigen zum Beispiel, dass zwei Arten von Ereignissen möglich sind, wenn Sie mit einer völlig ruhigen Flüssigkeit beginnen, beispielsweise mit einem Glas Wasser neben dem Bett. Das erste ist offensichtlich: Das Wasser beginnt in einem ruhigen Zustand und bleibt immer ruhig. Das zweite ist fantastisch, aber mathematisch möglich: Das Wasser beginnt in einem ruhigen Zustand, explodiert mitten in der Nacht und kehrt dann in einen ruhigen Zustand zurück.
„Dies beweist die mangelnde Einzigartigkeit, da aus den Anfangsdaten mindestens zwei Objekte erstellt werden können“, sagt Vikol.
Buckmaster und Wikol haben die Existenz vieler nicht eindeutiger schwacher Lösungen (nicht nur der beiden oben beschriebenen) der Navier-Stokes-Gleichungen bewiesen. Die Bedeutung dieser Beweise bleibt abzuwarten. Irgendwann können schwache Lösungen so schwach werden, dass sie nicht mehr mit glatteren Lösungen in Beziehung stehen, die nachgeahmt werden sollten. Wenn dies so ist, wird das von Bakmaster und Wikol erzielte Ergebnis zu wenig führen.
„Dieses Ergebnis ist eindeutig eine Warnung, aber man kann argumentieren, dass diese Warnung die schwächste Idee schwacher Entscheidungen betrifft. Es gibt viele Schichten stärkerer Lösungen, auf die Sie auf ein viel besseres Verhalten hoffen können “im Fall der Navier-Stokes-Gleichungen”, sagt De Lellis.
Backmaster und Wikol denken auch in Schichten, und er hat Lehrs Entscheidungen im Visier - um zu beweisen, dass sie auch mehrere Physik zulassen, in denen dieselbe Flüssigkeit aus demselben Zustand in Zukunft zu unterschiedlichen Formen kommen kann.
"Tristan und ich glauben, dass Lerays Entscheidungen nicht einzigartig sind. Wir haben dies noch nicht bewiesen, aber unsere Arbeit legt den Brückenkopf für einen Angriff auf diese Aufgabe “, sagte Vikol.