☘️ ♐️ 🏳️‍🌈 Quantenresiliente Blockchain 👩‍👧 💅🏿 💿

In diesem Artikel werde ich über das Sicherheitsproblem in der Blockchain-Technologie angesichts der Leistungssteigerung von Quantencomputern sprechen, einige der Methoden zum Schutz vor Angriffen mit einem Quantencomputer erörtern und ein aktuelles Projekt: Quantum-Resistant Ledger. Laut den Entwicklern wird dies die erste Plattform der Welt sein, die auf den Prinzipien der Post-Quanten-Verschlüsselung basiert und im Falle einer raschen Entwicklung dieser Technologien Schutz vor "Quantenschock" bietet. Plattformen, die nach klassischen Verschlüsselungsprinzipien erstellt wurden, können einem solchen Schlag ausgesetzt werden. Ohne grundlegende Änderungen könnten Bitcoin, Ethereum, Ardour und die meisten dieser Plattformen in naher Zukunft verfügbar sein.

Teil 1. Sicherheitsproblem

Sicherheitslücke

Der Schutzalgorithmus von Bitcoin und ähnlichen Systemen basiert auf dem Prinzip der asymmetrischen Verschlüsselung mit öffentlichen und privaten Schlüsseln. Eine Transaktion wird mit einem privaten Schlüssel signiert und ihre Gültigkeit wird mit dem öffentlichen Schlüssel überprüft.

Mit klassischen Angriffsalgorithmen ist es fast unmöglich, einen privaten Schlüssel zu finden, der den öffentlichen kennt. Asymmetrische Verschlüsselungssysteme wie RSA und dergleichen (DSA, DH usw.) basieren auf der Behauptung, dass die Komplexität der Faktorisierung einer Zahl exponentiell mit der Größe des Schlüssels zunimmt. Mit dem Shore-Algorithmus auf einem Quantencomputer wird es jedoch in Polynomzeit möglich, die Zahl in Primfaktoren zu zerlegen und so den privaten Schlüssel zu finden, der den öffentlichen kennt.

Im Jahr 2001 demonstrierte IBM dies, indem es die Zahl 15 in zwei Primfaktoren, 3 und 5, aufteilte. Für diese Zwecke wurde ein Quantencomputer verwendet, der aus 7 Qubits bestand. Seitdem ist die Entwicklung von Quantencomputertechnologien schneller vorangekommen.

2016 führt eine Gruppe von Forschern des Massachusetts Institute of Technology zusammen mit dem Innsbruck Institute die gleiche Aufgabe durch, die Zahl 15 mit nur 5 Qubits zu zerlegen.

Im Juli 2017 wurde von russisch-amerikanischen Physikern ein programmierbarer 51-Qubit-Computer entwickelt .

Ende Oktober 2017 kam eine internationale Forschungsgruppe von Universitäten in Singapur und Australien zu dem Schluss, dass die meisten in der Blockchain verwendeten kryptografischen Protokolle anfällig für Angriffe eines leistungsstarken Quantencomputers sind. Der Bericht der Gruppe enthält zwei Vorhersagen zum Leistungswachstum des Quantencomputers: optimistisch und weniger optimistisch. Nach dem ersten wird sich die Anzahl der Qubits eines Quantencomputers alle 10 Monate verdoppeln. Eine weniger optimistische Prognose deutet darauf hin, dass sich die Anzahl der Qubits alle 20 Monate verdoppelt. Die folgende Abbildung zeigt Diagramme beider Prognosen.

Am anfälligsten für Quantencomputerangriffe ist der Algorithmus zum Erstellen einer digitalen Signatur basierend auf elliptischen Kurven ( ECDSA ). Dem Bericht der Gruppe zufolge kann Bitcoin in seiner klassischen Form bis 2027 geknackt werden.

Vielleicht ist nicht alles so schlimm? Der öffentliche Schlüssel wird nicht im Klartext gespeichert

Ende April 2017 wurde auf bitcoin.com ein Artikel veröffentlicht, um die Frage zu beantworten, ob Bitcoin-Inhaber vorsichtig sein sollten, ihn mit einem Quantencomputer zu brechen. Trotz der Tatsache, dass in der Bitcoin-Blockchain asymmetrische Verschlüsselung verwendet wird, sollten sich Benutzer keine Sorgen um die Sicherheit ihrer Münzen machen. Der öffentliche Schlüssel wird nicht im Klartext gespeichert. Adressen zum Übertragen von Münzen sind also keine öffentlichen Schlüssel, sondern nur das Ergebnis der Anwendung der SHA-256-Hash-Funktion. Die Hash-Funktion führt eine Einwegkonvertierung durch und ist daher resistent gegen die Angriffe eines Quantencomputers.

Der öffentliche Schlüssel wird während der Transaktion bekannt

Die Aussage, dass der öffentliche Schlüssel im Klartext nicht verfügbar ist, ist nicht ganz richtig. Ohne auf kleine Details einzugehen, werden wir am Beispiel von Bitcoin (BTC) analysieren, wie die Kryptowährung von einer Person zur anderen übertragen wird.

Lassen Sie Alice in ihrer Brieftasche auf einer der Bitcoin-Adressen 100 mBTC (1000 mBTC = 1 BTC) haben. Sie will Bob 1 mBTC übertragen. Dazu gibt sie Bobs Bitcoin-Adresse, die Überweisungsgebühr und die Bitcoin-Adresse in ihrer Brieftasche an, um Änderungen zu erhalten. Angenommen, Alice hat 1 mBTC als Provision angegeben. Von 100 mBTC, die Alice hat, wird 1 mBTC an Bob gesendet, 1 mBTC als Provision im Bitcoin-Netzwerk und 98 mBTC an Alice 'Brieftasche zurückgegeben.

Nun wollen wir sehen, was auf Bitcoin-Netzwerkebene passiert. Alice und Bob haben Brieftaschen mit Adressen zum Aufbewahren von Münzen. Eine Brieftasche kann mehrere Bitcoin-Adressen enthalten. Beim Erstellen von Brieftaschen werden Adressen generiert. Jede Adresse entspricht einem vom ECDSA-Algorithmus erstellten Schlüsselpaar: öffentlich und privat. Beim Übertragen von Münzen wird eine Transaktion erstellt, in der Informationen über die Anzahl der von Alice übertragenen Münzen, die Bitcoin-Adresse von Bob, eine Signatur mit dem privaten Schlüssel von Alice, den öffentlichen Schlüssel von Alice und einige andere Daten übertragen werden. Als nächstes wird die Transaktion in einer offenen (unverschlüsselten) Form an das Netzwerk gesendet . Bevor Hosts eine Transaktion zur Verarbeitung akzeptieren, überprüfen sie ihre Signatur mit dem öffentlichen Schlüssel. Wenn die Signatur gültig ist, fügen sie dem Block Transaktionsinformationen hinzu. Dieser Schaltvorgang wird als Bestätigung bezeichnet.

Die durchschnittliche Blockgenerierungszeit im Bitcoin-Netzwerk beträgt 10 Minuten. Das Netzwerk versucht, diese Zeit konstant zu halten. Es wird empfohlen, vor der Verwendung der erhaltenen Mittel auf 6 Bestätigungen zu warten. Auf diese Weise kann Bob unter Beachtung der Sicherheitsregeln die erhaltenen Mittel etwa eine Stunde nach ihrer Überweisung verwenden.

Eine der Funktionen beim Übertragen von Münzen im Bitcoin-Netzwerk besteht darin, dass nicht nur ein Teil der Münzen von einer Adresse übertragen werden kann. Münzen werden immer vollständig übertragen und befinden sich an der Bitcoin-Adresse der Brieftasche. Die Änderung wird an den Absender zurückgesandt. Es kann sowohl an die Adresse, von der die Münzen gesendet wurden, als auch an jede andere Adresse bezogen werden. Daher muss Alice die Lieferadresse angeben. In einer Reihe von Software, die die Brieftasche bedient, ist die Lieferadresse die Sendeadresse.

Eine Transaktionsgebühr ist streng genommen nicht obligatorisch, aber ihre Abwesenheit kann die Transaktion für eine lange Zeit verzögern. Das Gegenteil ist auch der Fall: Sie können die Transaktion etwas beschleunigen, indem Sie die Provisionsgröße erhöhen. Zum Zeitpunkt dieses Schreibens (Januar 2018) bietet die meiste Brieftaschensoftware eine Gebühr von 1 mBTC. Es gibt beispielsweise eine Reihe von Ressourcen, mit denen Sie die Zeit schätzen können, zu der eine Transaktion in einem Block enthalten ist, abhängig von der Höhe der Provision.

1 Mal den öffentlichen Schlüssel verwenden

Aus Sicherheitsgründen ist es am besten, eine Änderung an einer neuen Adresse zu erhalten, deren öffentlicher Schlüssel dem Netzwerk nicht bekannt ist. In diesem Fall wird das Schlüsselpaar nur einmal verwendet. Laut Statistik vom Dezember 2017 werden jedoch etwa 41,34% der Adressen wiederverwendet.

10 Minuten zum Angriff

Früher oder später müssen Sie das Geld jedoch an der neuen Adresse verwenden. Der öffentliche Schlüssel wird im Klartext an das Netzwerk übertragen. Bis zur Bestätigung ist das Geld noch beim Absender. Wenn ein Angreifer während einer Transaktion einen öffentlichen Schlüssel erhält, hat er etwa 10 Minuten Zeit, um den privaten Schlüssel mithilfe eines Quantencomputers abzurufen und zu versuchen, seine Transaktion von derselben Adresse aus durchzuführen, wodurch eine höhere Provision festgelegt wird.

Statische Adressen sind anfälliger

In Systemen wie Ethereum, NXT, Ardour usw. wird der öffentliche Schlüssel auch nach der ersten Transaktion bekannt. Die Situation wird durch die Tatsache verschärft, dass Token oder intelligente Verträge an statische Adressen gebunden sind, die für lange Zeit angegriffen werden können. Wenn der Angriff erfolgreich ist, kann der Angreifer das gesamte Wirtschaftssystem anhand dieser Adressen zerstören.

Teil 2. Lösungen

Wie kann man Widerstand gegen Angriffe eines Quantencomputers leisten?

Derzeit gibt es mehrere grundlegende Methoden, die Schutz vor Quantencomputerangriffen bieten:

Hash-basierte Kryptographie;
Code-basierte Kryptographie;
Matrix-basierte Kryptographie;
Kryptographie basierend auf mehrdimensionalen quadratischen Systemen;
Kryptographie mit privatem Schlüssel.

Mit ausreichend langen Schlüsseln und der Einhaltung der Sicherheitsanforderungen können diese Schutzmethoden sowohl klassischen Angriffen als auch Angriffen mit einem Quantencomputer standhalten.

Am besten untersucht wird die Verwendung digitaler Signaturen basierend auf Hash-Funktionen.

Wie bereits erwähnt, führt die Hash-Funktion eine Einwegnachrichtenkonvertierung durch. Die Nachricht wird in einen Hashwert fester Länge konvertiert. Die Verwendung einer Hash-Funktion sollte es einerseits sinnlos machen, Nachrichten zu durchsuchen, um einen ähnlichen Hash-Wert zu erhalten. Andererseits muss der Algorithmus kollisionssicher sein: Wenn 2 verschiedene Nachrichten dem gleichen Wert der Hash-Funktion entsprechen.

Der Quantenalgorithmus von Grover kann verwendet werden, um zu versuchen, eine Kollision zu finden, oder um einen vorläufigen Angriff durchzuführen, um die ursprüngliche Nachricht zu finden. Dies erfordert

$O (2 ^ {\ frac {n} {2}})$ Operationen. Um die 128-Bit-Sicherheit aufrechtzuerhalten, beträgt die Länge des resultierenden Hash mindestens 256 Bit. Als solche Funktion kann SHA-256 ausgewählt werden.

Lampport Unterschrift

Eine Option für die Verwendung einer Hash-Funktion in einer digitalen Signatur ist die Signatur von Lamport. Es kann auf der Basis einer beliebigen Einweg-Hash-Funktion erstellt werden. Die kryptografische Stabilität des Algorithmus basiert auf der kryptografischen Stabilität der verwendeten Hash-Funktionen.

Signaturschema

Für Nachricht

$M$ lang

$m$ Schlüssel werden generiert. Zunächst werden private Schlüssel paarweise generiert

$SK$ lang

$n$ Dann werden unter Verwendung einer Hash-Funktion öffentliche Schlüsselpaare aus privaten Schlüsseln gebildet

$PK$ . Die Anzahl der privaten und öffentlichen Schlüsselpaare entspricht der Anzahl der Bits in der ursprünglichen Nachricht.

Beim Signieren wird eine Nachricht Stück für Stück gelesen und abhängig vom Wert des aktuellen Bits wird einer der privaten Schlüssel des entsprechenden Paares ausgewählt. Ausgewählte private Schlüssel werden zu einer Signatur zusammengefasst. Als nächstes die resultierende Signatur und

$m$ Paare öffentlicher Schlüssel werden an den Empfänger gesendet.

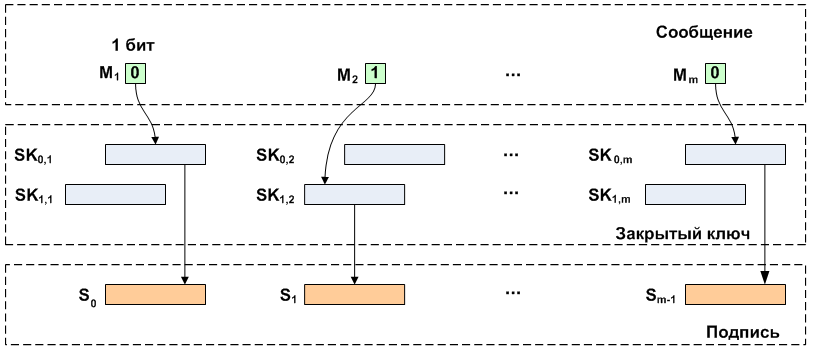
Das Überprüfen einer Signatur ähnelt dem Erstellen. Die Signatur ist in Längenfragmente unterteilt

$n$ Diese werden dann mit derselben Hash-Funktion konvertiert. Die Nachricht wird Stück für Stück gelesen und der Wert des Bits wählt den öffentlichen Schlüssel aus, der mit dem empfangenen Hashwert verglichen wird.

In der Regel wird die ursprüngliche Nachricht vor dem Anwenden einer Signatur gehasht, um ihre Größe zu verringern. Dann sei SHA-256 als Hash-Funktion ausgewählt

$m = n = 256$ . In diesem Fall die Gesamtlänge des öffentlichen (sowie des privaten) Schlüssels

$L_ {PK}$ Es stellt sich heraus, gleich:

$L_ {PK} = n * 2 * m = 256 * 2 * 256 = 128 KB = 16 KB.$

Signaturlänge

$L_S$ ist:

$L_S = n * m = 64 KB = 8 KB.$

Die Signatur von Lamport ist einmalig (bleibt nur dann sicher, wenn sie einmal verwendet wird), da bei Ausführung und Übertragung die Hälfte des privaten Schlüssels bekannt wird. Die Nachrichtenlänge sei 256 Byte und die Hash-Länge 256. Bevor Alice die Signatur für die Nachricht veröffentlicht, kennt niemand 2 * 256 Zufallszahlen in einem geheimen Schlüssel. Somit kann niemand den richtigen Satz von 256 Nummern für die Signatur erstellen.

Nachdem Alice die Signatur veröffentlicht hat, kennt niemand mehr die verbleibenden 256 Nummern und kann daher keine Signatur für Nachrichten mit einem anderen Hash erstellen.

Die Tatsache, dass Lamports Signatur einmalig ist, kombiniert mit einer beeindruckenden Gesamtmenge an Signatur und öffentlichem Schlüssel (24 KB mit einer Nachrichtenlänge von 256 Bytes und einer Hash-Länge von 256 Bytes), macht die Verwendung in einem öffentlichen Transaktionsblock unangemessen.

Unterschrift Winternitz

Es gibt andere einmalige Algorithmen für digitale Signaturen. In der Signatur von Vinternytsia ist die ursprüngliche Nachricht im Gegensatz zur Signatur von Lamport nicht bitweise, sondern blockweise signiert. Die einmalige Signatur von Winternitz kann wie Lamport auf der Grundlage jeder starken kryptografischen Funktion erstellt werden.

Signaturschema

Nachricht

$M$ lang

$m$ in Fragmente zerbrochen

$M_i$ lang

$w$ . Für jedes Fragment wird ein privater Schlüssel generiert

$SK$ Längen

$n$ . Für jeden privaten Schlüssel wird nacheinander eine Hash-Operation angewendet

$2 ^ w-1$ Zeiten (Runden

$R$ ) Als Ergebnis der Operationen werden die entsprechenden öffentlichen Schlüssel erhalten

$PK$ gleiche Länge

$n$ .

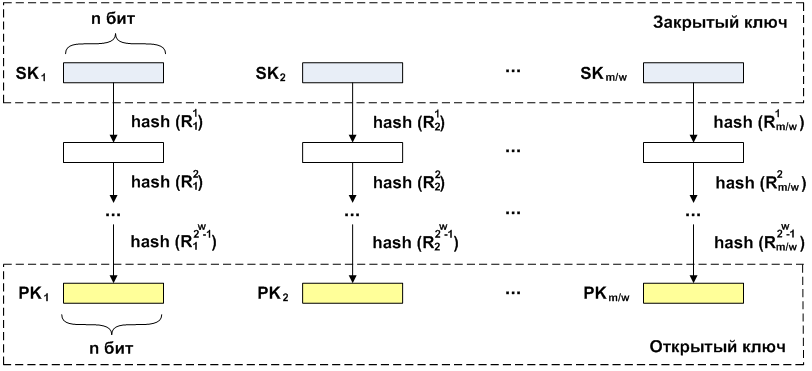
Beim Signieren wird wie bei der Generierung öffentlicher Schlüssel eine iterative Berechnung des Hash über die privaten Schlüssel durchgeführt. Die Anzahl der Wiederholungen hängt jeweils von der zu signierenden Nachricht ab. Wie bereits erwähnt, ist die Nachricht in Längenblöcke unterteilt

$w$ . Der numerische Wert dieses Blocks

$M_i$ und ist die Anzahl der Iterationen, die für private Schlüssel ausgeführt werden müssen, um eine Signatur zu erhalten. Die Verbindung der empfangenen Blöcke ist die Signatur dieser Nachricht.

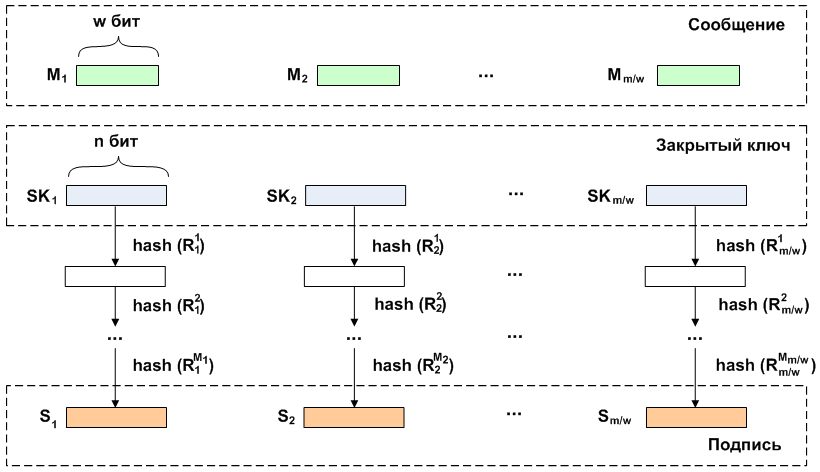
Beim Überprüfen einer Signatur auf Fragmente ihrer Länge

$n$ berechnet iterativ den Hash. Anzahl der Runden

$R_i$ Die Anwendung der Hash-Funktion ist definiert als die Differenz zwischen der Anzahl der Iterationen zum Erhalten des öffentlichen Schlüssels und dem numerischen Wert des Nachrichtenblocks, d. h.

$R_i = 2 ^ w-1 - M_i$ mal. Dann werden die erhaltenen Werte mit dem entsprechenden öffentlichen Schlüssel verglichen.

Beispiel

Ich werde das Obige mit einem kleinen Beispiel veranschaulichen. Lassen Sie die Nachricht gegeben werden

$M$ (in Bitdarstellung) Länge

$m$ , Parameter Vinternitsa

$w$ und einige Hash-Funktion der Länge

$n$ ::

$M = 11000111 \: 01100111, m = 16, \: w = 8, \: n = 256.$

Generieren

$m / w = 2$ privater Schlüssel basierend auf einem Pseudozufallszahlengenerator. Für jeden privaten Schlüssel wenden wir an

$2 ^ w-1 = $ 25$ mal eine Hash-Funktion, dabei bekommen

$2$ öffentliche Schlüssel, die zu einem gemeinsamen Längenschlüssel kombiniert werden

$2 * n = 512$ bisschen. Weiter für jeden Nachrichtenblock

$M$ Längen

$w$ Bestimmen Sie die Anzahl der Hash-Operationen, die auf den privaten Schlüssel angewendet werden

$R_i$ . In diesem Fall sind dies die Werte

$11000111_2 = 199_ {10}$ und

$01100111_2 = 103_ {10}$ entsprechend. Nachdem wir den Hashing-Vorgang für private Schlüssel ausgeführt haben, erhalten wir eine Signatur der Länge

$2 * n = 512$ bisschen.

Um die Signatur zu überprüfen, teilen Sie sie in Teile der Länge

$n$ . Wir produzieren über jedes Teil

$R_i = 2 ^ w-1 - M_i$ Hash-Operationen. Das heißt,

$255 - 199 = 56$ und

$255 - 103 = $ 15$ mal jeweils. Wenn das Ergebnis der Operationen zu einem Wert führt, der mit dem öffentlichen Schlüssel übereinstimmt, ist die Nachricht zuverlässig.

Wenn Sie SHA-256 als Hash-Funktion zum Signieren von Winternitz verwenden,

$m = n = 256$ .

Lass

$w = 8$ bisschen. Dann die volle Größe des öffentlichen Schlüssels

$L_ {PK}$ und Unterschriften

$L_S$ gleich:

$L_ {PK} = L_S = m / w * n = 256/8 * 256 = 8 KB = 1 KB.$

Die Anzahl der Hash-Berechnungsoperationen ist in diesem Fall gleich:

$P = (2 ^ w-1) * m / w = (2 ^ 8-1) * 256/8 = 8160.$

Für den Fall von

$w = 16$ erhöht sich dieser Wert auf

$P = 1048560$ .

Die Größe des öffentlichen Schlüssels und der Signatur mit denselben Parametern wie im Beispiel für die Lamport-Signatur beträgt 1 KB. Insgesamt ist dies weniger als in der Unterschrift von Lamport (24 KB). In diesem Fall beträgt die Anzahl der Hash-Berechnungen jedoch 8160. Das ist natürlich sehr viel. Außerdem wird beim Überprüfen der Signatur durchschnittlich die Hälfte dieser Anzahl von Iterationen ausgeführt. Dies macht diese Signaturoption für die Verwendung in der Blockchain ungeeignet.

Es gibt verschiedene Möglichkeiten, Winternitz zu signieren, einschließlich der Erweiterung der Signatur, um die Zuverlässigkeit zu erhöhen und die Anzahl der Verwendungen der Hash-Funktion zu verringern. Ihre Beschreibung würde den Rahmen dieses Artikels sprengen. Interessenten können hier mehr sehen . Die Anwendung der Signatur Vinternitsa basierend auf der inländischen Hash-Funktion GOST 34.11-12 ist hier zu sehen.

Merkle Tree (MSS)

Einmalige Signaturen können eine zufriedenstellende kryptografische Sicherheit bieten. Ihre einmalige Verwendung kann jedoch zu einem ernsthaften Problem werden. Lassen Sie es notwendig sein, Einsparungen von einer Adresse zur anderen zu übertragen. Es stellt sich heraus, dass bei Verwendung von einmaligen Signaturen jedes Mal der gesamte Geldbetrag überwiesen werden muss und für jede Transaktion eine neue Adresse benötigt wird. Bei jeder Transaktion müssen Sie einen neuen öffentlichen Schlüssel veröffentlichen. Darüber hinaus benötigt das Speichern neuer Transaktionen in der Blockchain nach und nach mehr Zeit, um nach ihnen zu suchen.

Um das Problem zu lösen, erweitern sie das Signaturschema, indem sie mehrere Signaturen basierend auf mehreren Schlüsselpaaren für jede Adresse durchführen. Die Verwendung mehrerer Signaturen erfolgt auf der Grundlage eines binären Hash-Baums - des Merkle-Baums.

Weitere Details

Die Berechnung eines Baumes erfolgt von den Blättern bis zur Wurzel. Jedes Knotenblatt des Baums wird als Hash aus dem generierten öffentlichen Schlüssel berechnet. Die verbleibenden Knoten werden berechnet, indem ein Hash aus der Verkettung (Verkleben) der untergeordneten Knoten erhalten wird. Somit wird der gesamte Baum bis zur Wurzel berechnet. Angenommen, es gibt 4 Schlüsselpaare. Der Merkle-Baum wird durch Berechnung von 7 Hashes berechnet (siehe Abbildung oben).

Ein Merkmal des Merkle-Baums ist, dass die Existenz eines Knotens oder Blattes durch Berechnung der Wurzel kryptografisch nachgewiesen werden kann.

Die Nachrichtensignatur wird mit dem privaten Schlüssel aus dem ausgewählten Schlüsselpaar erstellt.

Bei der Signaturüberprüfung wird der Stamm anhand der übergebenen Parameter berechnet und mit einem wiederverwendbaren öffentlichen Schlüssel verglichen. Diese Parameter sind:

Unterschrift
Wurzel
einmaliger Schlüssel, dessen geschlossener Teil die Nachricht signiert wurde;
Baumhashes, die auf dem Weg vom ausgewählten Blatt zur Wurzel liegen.

Bei Verwendung von einmaligen Merkle- oder Winternitz-Signaturen muss kein separat ausgewählter einmaliger öffentlicher Schlüssel übertragen werden, da dieser aus der Nachrichtensignatur abgerufen werden kann. Es reicht aus, seine Nummer zu übergeben, was seine Position im Baum widerspiegelt. , : , , — 0 (

$PK1$ )

$H2$

$H6$ .

$PK1$ , ,

$H1$ .

$H1$

$H2$

$H5$ .

$H5$

$H6$

$R$ , .

Der Merkle-Baum, der aus öffentlichen Schlüsseln kompiliert und berechnet wird, ermöglicht es, anstatt die gesamte Gruppe von Schlüsseln zu veröffentlichen, nur die Wurzel des Baums zu veröffentlichen. Dies erhöht die Größe der Signatur, indem ein Teil des Baums in die Signatur aufgenommen wird. Es ist jedoch möglich, nur 1 Hash zu verwenden, um viele Signaturen zu überprüfen. Also mit der Tiefe des Baumes

kann unterschrieben werden

$N$

Beiträge. Der Merkle-Baum für Schlüssel, der auf dem Algorithmus der elliptischen Kurve basiert, wird in Bitcoin und Ethereum verwendet. Zu letzterem gibt es einen ausgezeichnetenArtikelmit einer Untersuchung des Merkle-Baums.

$2^N$

Hyperbäume

Der Hauptnachteil des Merkle-Grundschemas besteht darin, dass die Anzahl der verfügbaren Signaturen begrenzt ist und alle Schlüsselpaare einmaliger Signaturen generiert werden müssen, bevor der Merkle-Baum berechnet wird. Die Schlüsselgenerierung und die Signaturzeit nehmen in Bezug auf die Baumhöhe exponentiell zu. Bei Verwendung eines Hyperbaums ist es möglich, die Generierung neuer Schlüssel zu verzögern und die Anzahl der verfügbaren Paare zu erhöhen.

Weitere Details

, . 2 : . , . . , (. ).

, , . , , . , .

. . , , .

Erweiterte Merkle-Baumstruktur (XMSS)

Eine vollständige Beschreibung der Schaltung geht weit über den Rahmen dieses Artikels hinaus. Weitere Einzelheiten finden Sie hier . Ich werde nur auf grundlegende Konzepte und Eigenschaften eingehen. Mit dem XMSS-Schema können Sie wie mit dem Merkle-Baum einmalige Signaturen erweitern. Die Verwendung einer Bitmaske unter Verwendung von exklusiven ORs (XOR) der untergeordneten Knoten, bevor die Hashes mit dem übergeordneten Knoten verknüpft werden, ermöglicht es, den Widerstand der verwendeten Hash-Funktionen gegen Kollisionen zu erhöhen. Wenn Sie also SHA-256 als Hash-Funktion in Kombination mit einem erweiterten Schema verwenden, können Sie mit Winternitz mit einem Sicherheitsparameter (W-OTS +) die Sicherheit von 128 auf 196 Bit erhöhen. Laut lenstraDie 196-Bit-Verteidigung reicht aus, um bis 2169 durch einen einfachen Brute-Force-Angriff als sicher gegen Angriffe angesehen zu werden. Bei allen Vorteilen des XMSS-Schemas ist der Hauptnachteil die lange Schlüsselgenerierungszeit.

Derzeit gibt es andere Merkle-Baumerweiterungsschemata ( GMSS , CMSS ), die in Kombination mit Einmal-Signatur-Algorithmen auch in einer Blockchain verwendet werden können, die gegen Angriffe mit einem Quantencomputer resistent ist.

Teil 3. Umsetzung von Ideen

Quantum Sustainable Blockchain Project - QRL

In der zweiten Jahreshälfte 2016 gründete Dr. P. Waterland eine Gruppe, um eine Blockchain zu entwickeln, die sowohl für klassische Angriffe als auch für Angriffe mit einem Quantencomputer stabil ist. Nach den Ergebnissen der Entwicklung des theoretischen Teils Ende desselben Jahres wurde das Hauptdokument der entwickelten Blockchain, das „Weißbuch“ (Weißbuch), öffentlich zugänglich gemacht. Das Dokument ist derzeit in mehreren Sprachen verfügbar, einschließlich Russisch.

Hauptmerkmale von QRL

1. Signaturschema und Sicherheit
Ein Signaturschema wird basierend auf dem erweiterten Winternitz-Signaturalgorithmus (W-OTS +, w = 16, SHA-256) basierend auf XMSS-verbundenen Strukturen angewendet. Mit diesem Ansatz können Sie Adressen mit der Möglichkeit des Signierens generieren und so die lange Rechenverzögerung vermeiden, die beim Erstellen von riesigen XMSS-Konstrukten auftritt. Bietet 196-Bit-Schutz mit vorhersehbarer Sicherheit gegen Angriffe durch einfache Aufzählung bis 2169.

2. Konsensalgorithmus - Arbeitsnachweis
In der ersten Iteration des Hauptnetzwerks wurde ein Konsensalgorithmus zum Nachweis der Arbeit angekündigt.

3. Floating Commission
Größere Transaktionsgrößen im Vergleich zu anderen Blöcken der Transaktionskette erfordern die Zahlung für jede Transaktion. Laut Waterland werden Märkte mit einer künstlichen Provision (z. B. Bitcoin) nicht benötigt und widersprechen dem Ideal einer offenen Blockchain. Jede Transaktion muss, sofern sie von einer Mindestzahlung begleitet wird, genauso gültig sein wie jede andere. Der für Bergleute akzeptable Mindestzahlungsbetrag sollte variabel sein und vom Markt festgelegt werden. Das heißt, Knoten (Bergleute) müssen wettbewerbsfähig eine untere Grenze für die Zahlung untereinander festlegen. Der absolute Mindestwert wird auf Protokollebene eingehalten. Daher bestellen Bergleute nach eigenem Ermessen Transaktionen aus dem Mempool zur Aufnahme in den Block.

4. Dynamische Blockbelohnungsberechnung
Jeder neu erstellte Block enthält die erste Coinbase-Transaktion mit der Mining-Adresse, für die die Belohnung als Belohnungsbetrag für die Münzrate mit dem Gesamtbetrag der Provisionen für Transaktionen innerhalb des Blocks definiert wird.

5. Die Zeit, die die Blöcke verbringen, beträgt 1 Minute
Die Zeit zwischen den Blöcken im Bitcoin-Netzwerk beträgt ungefähr 10 Minuten. Mit den erforderlichen 6 Bestätigungen erhöht sich zusätzlich die Wartezeit bis zum Abschluss der Transaktion. Neuere Transaktionskettenblockschemata wie Ethereum werden in diesem Aspekt verbessert und profitieren von einer kürzeren Blockierungszeit, ohne die Sicherheit zu verlieren oder Bergleute zu zentralisieren, da verwaiste / veraltete Blöcke häufig auftreten.

Für QRL beträgt diese Blockierungszeit 1 Minute.

6. Adaptive Blockgröße
Um mögliche Streitigkeiten zu vermeiden, wurde eine vorgefertigte adaptive Lösung basierend auf dem Bitpay-Vorschlag modelliert, bei der ein Multiplikator verwendet wird, um die Blockgröße zu erhöhen

$x$ mittelgroß

$y$ der letzte

$z$ Blöcke. Die Verwendung eines Durchschnittswerts ermöglicht es Bergleuten nicht, zu manipulieren, einschließlich leerer oder übergelaufener Blöcke, um die durchschnittliche Blockgröße zu ändern.

$x$ und

$z$ dann wird es strenge Konsensregeln für das Netzwerk geben, die eingehalten werden müssen. Somit ist die maximale Blockgröße

$b$ kann einfach berechnet werden als:

$b = xy$ .

7. Währung - Quantum
Die Basiswährungseinheit ist ein Quantum. Jedes Quant ist in die kleinsten Elemente unterteilt. Nachfolgend sind die Namen aller Elemente in aufsteigender Reihenfolge aufgeführt:

Artikel	Wert
Ufer	$1$
Nakamoto	$10 ^ 3$
Buterin	$10 ^ 6$
Merkle	$10 ^ {10}$
Lampport	$10 ^ {13}$
Quantum	$10 ^ {16}$

Somit ist jede Transaktion, an der ein Teil des Quantums beteiligt ist, tatsächlich eine sehr große Anzahl von Shore-Einheiten. Die Transaktionsgebühr wird berechnet und in Shore-Einheiten gebucht.

8. Konten und Adressen
Benutzersalden werden auf Konten gespeichert. Jedes Konto ist eine eindeutige, wiederverwendbare Blockadresse für die Transaktionskette, die durch eine Zeile angezeigt wird, die mit „Q“ beginnt.

Die Adresse wird durch Ausführen von SHA-256 an der Merkle-Wurzel des höchsten XMSS-Zertifizierungsbaums erstellt. Hinzu kommt eine 4-Byte-Prüfsumme, die aus den ersten vier Bytes des doppelten SHA-256-Hash der Merkle-Wurzel und dem Buchstaben „Q“ besteht.

In Python-Pseudocode wird dies beispielsweise wie folgt beschrieben:

Q + sha256(merkle root) + sha256(sha256(merkle root))[: 4]

Typische Kontoadresse:
Qcea29b1402248d53469e352de662923986f3a94cf0f51522bedd08fb5e64948af479

Jedes Konto hat einen Saldo, der auf Quanten lautet und bis zu einer einzelnen Shore-Einheit teilbar ist. Adressen verwenden bei jeder Transaktion ein neues Paar einmaliger Signaturschlüssel. Ein Transaktionszähler namens nonce erhöht sich mit jeder von Ihrem Konto gesendeten Transaktion. Auf diese Weise können Brieftaschen, in denen nicht die gesamte Blockkette gespeichert ist, ihre Position im Hypertree-Signaturschema unter Beibehaltung des Status verfolgen.

Aktueller Stand des Projekts und Pläne für die Zukunft

Nach der Veröffentlichung des "White Papers" wurde die Gruppe mit mehreren neuen Entwicklern aufgefüllt und die Arbeit an der Umsetzung des Plans begann. Auf der Projektwebsite wurden regelmäßig Fortschrittsberichte veröffentlicht. Bis April 2017 war das QRL-Blockchain-Testnetzwerk bereits gestartet. Der Quellcode des Projekts wird auf Github veröffentlicht. Das Projekt wird bei Bitcointalk und Reddit aktiv diskutiert.

Im Mai 2017 wurde ein ICO im Ethereum-Ökosystem durchgeführt. ERC20 QRL-Token ausgestellt. Insgesamt wurden 65 Millionen Token ausgegeben. Davon sind 52 Millionen Token im Umlauf. Im Laufe von 200 Jahren werden schrittweise weitere 40 Millionen Münzen ausgegeben. Das Gesamtausgabenvolumen beträgt somit 105 Millionen Münzen. Wenn das Hauptnetzwerk gestartet wird, können diese Token im Verhältnis 1: 1 gegen QRL-Münzen ausgetauscht werden. Derzeit sind Token an Börsen wie Bittrex, Upbit und Liqui erhältlich. QRL-Zitate sind laut der Website coinmarketcap.com in den folgenden Abbildungen dargestellt.

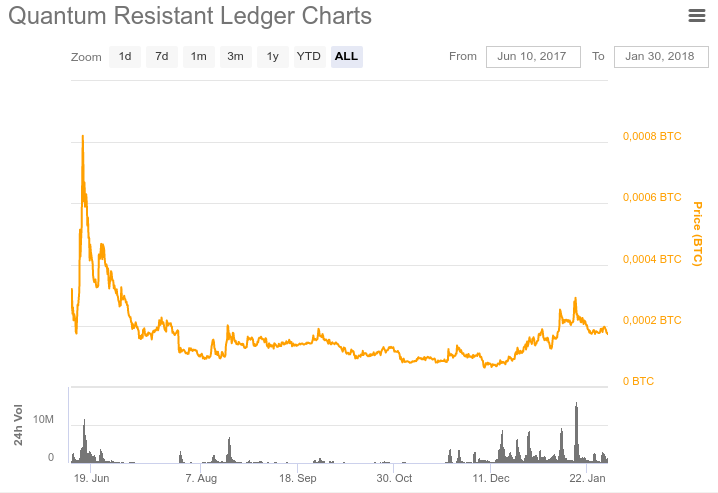
Der Start des Hauptnetzes ist für Februar bis März 2018 geplant.

In Zukunft ist geplant, den Konsensalgorithmus von der Bestätigung der Arbeit zur Bestätigung des Einsatzes (Nachweis des Einsatzes) zu ändern. Die erwartete sichere Verweilzeit der Blöcke beträgt 15 bis 30 Sekunden.

Fazit

Der Fortschritt der Quantentechnologien wurde eingeleitet und kann nicht gestoppt werden. Da immer produktivere Quantenmaschinen auftauchen, wird das Spektrum der Aufgaben, die sie lösen, kontinuierlich wachsen. Das Hacken einer vorhandenen Kryptoabwehr, die nicht an die Angriffe eines Quantencomputers angepasst ist, ist seit langem eines der zentralen Themen vieler Sicherheitsforen .

QRL ist die erste Blockchain-Technologie, mit der dieses Problem gelöst werden kann. In Zukunft werden natürlich andere auftauchen. Welcher von ihnen am erfolgreichsten sein wird - die Zeit wird es zeigen.

Danksagung

Der Autor ist Kamnik für die Vorbereitung eines wesentlichen Teils des Materials und insbesondere des technischen Teils sowie SannX für konstruktive Kritik und Korrekturen dankbar .

Referenzen

Zusätzliches Material

Ist ein Quantencomputer für Bitcoin gefährlich ?

Quantenresiliente Blockchain